基于“四基”的数学分层作业设计
徐春红
【摘要】从“四基”的维度来探讨初中数学分层作业设计策略问题,重点结合“四基”的要求,针对当前初中数学作业设计的不足,从设计分层作业、完善分层作业评价、增强作业导向性等三个方面探讨了初中数学作业分层设计的具体策略,旨在优化课堂学习效果。
【关键词】初中数学;分层作业;学习效果
作业是检验学生课堂所学知识掌握情况、帮助教师做好教学设计的重要载体。针对学生个体差异,教师设计分层作业,是提升作业质量的有效路径。
一、“四基”在初中数学教学及作业设计中的应用概述
《义务教育数学课程标准(2017年版2022年修订)》中明确指出“课程目标以学生发展为本,以核心素养为导向,进一步强调使学生获得数学‘四基经验”,强调运用新的数学知识、数学方法来发现问题、分析问题以及解决问题。“四基”理论主要指的是基础知识、基本技能、基本思想以及基本活动经验四个方面的内容,具有严谨形成理性、记忆通向理解、重复依靠变式、速度赢得效率的典型特征。本质上来看,“四基”是培养初中学生数学学科核心素养、实现数学学科教学目标的“根基”,而核心素养则是对“四基”的传承、发展,是“四基”效果在教学实践中的具体体现。将“四基理论”与初中数学教学、学生数学核心素养培育有机地融合在一起,有助于突出初中数学教学对象的具体性、目标明确性、过程发展性以及教学系统整体性,兼顾知识传授与能力提升的平衡,在动态的教学过程中促进数学学科教学任务、目标的达成。
二、活用“四基”,优化初中数学分层作业设计
1.坚持以生为本,遵循学生主体性原则
基础知识、基本技能、基本思想、基本活动经验等四个方面是相辅相成、相互交融、密切联系的整体,“四基”导向下的初中数学作业分层设计应在突出学生主体性前提下,遵循过程性、逻辑递进性、整体性以及发展性的基本原则,学中知、习中感、感中悟,巩固课堂所学知识、借助作业提升技能、培育数学思维、积累数学实践经验,循序渐进、有层次地引导学生由目前的发展区向最近发展区“发展”。从目前教学经验来看,初中数学在作业设计方面应当坚持两点基本原则:(1)提高作业设计有效性。作业本身应当有着巩固、检验和反馈等多方面的作用,尤其是在“双减”政策背景之下作业的价值会越发明显,同时教师在设计和布置作业时应当尽可能强化作业的教学效果,从而做到事半功倍。在教学中需要结合精简、准确的作业设计实现对教育功能的挖掘,尽可能规避机械化与重复性的作业内容,积极引导学生在作业完成的同时形成独立思考的意识习惯,从而提高学生的数学学习能力。(2)注重作业设计梯度性。作业设计过程中应当结合不同的学习成绩设计对应的作业,同时需要尽可能保障作业设计的合理性与针对性。例如对于优秀学生,作业设计应当充分发挥提升教学的作用;对于中等学生,作业设计应当带有培优的教学作用;对于后进生,作业设计应当带有知识的夯实巩固作用。在作业设计时应当尽可能展现教学梯度性的特征,基于不同难度、不同内容的作业让所有学生均可以得到提升和发展。
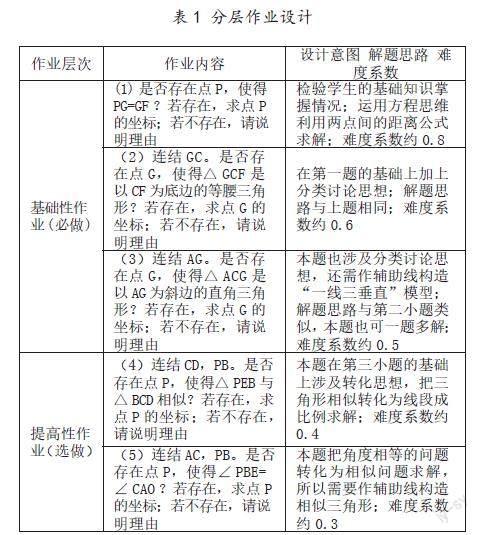
以“二次函数中动态几何存在性问题”作业分层设计为例,笔者设计了分层作业显示在课件中。本题笔者以“已知抛物线y=ax3+bx+3与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,顶点为点D,点P是抛物线在第一象限内的一个动点,过点P做PE⊥x軸于点E,分别交线段BC、BD于点F、G”为题干设计了5个难度系数逐渐加深的分层作业(表1见下页),由浅入深地概括了用线段来解决动态几何存在性问题的解题技巧、解题方法及所用到的数学基本思想。“四基”的应用,核心就是要从学生的角度来完成教学设计、开展教学以及作业设计,突出学生的主体地位。
表1 分层作业设计
2.理论与实践相结合,科学设计分层作业
教师在设计初中数学分层作业过程中,要充分考虑学生的个体差异,并结合学生所掌握的初中数学基础知识、基本技能、基本思想以及基本活动经验等实际情况以及具体的数学模块的教学情况来科学、合理地予以分层,既要注重对所教授知识的巩固,又必须能够针对学生的水平设计针对性强、实效性强的作业,严格把控好作业的难度分层、做题的时限,拓宽学生的解题思路和数学知识运用的路径,优化作业设计、巩固课堂教学效果的同时,为培养学生的创新力、创造力奠定坚实基础。同时,还必须要把控好分层作业的“总量”,学优生宜以中等难度的作业为主,并适当增加难度大、开放性的题目,引导他们去主动思考、提升数学技能、培育数学思想,在积累数学知识经验的过程中实现知识与能力的共同提升;对于中等学生,则应该多设计些中等难度的题目,并融入一两个“拦路虎”,让学生在固定时间内完成常规作业的同时,主动去探索新知,拓展他们的知识面;知识掌握不牢固的学生,应以基本知识练习为主,熟能生巧,基本知识掌握好了,学生潜移默化中就会提升观察问题、分析问题以及解决问题的能力和水平,初中数学知识传授、数学学科素养培育也就水到渠成了。以“二次函数的面积”专题复习教学为例,笔者设计了以下分层作业。
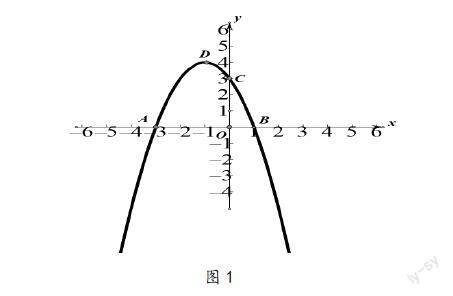
如图1,抛物线与x轴交于点A、B,与y轴交于点C(0,3),顶点坐标是D(-1,4)。(前面三题为必做题,时间20分钟,最后一问为选做题)
(1)求抛物线的函数解析式。
(2)连接AC、AD、BC、DC:
①求△ABC的面积;
②求△ADC的面积。
(3)若点P(m,n)是直线AC上方抛物线上的动点,写出△PAC的面积S关于m的函数关系式。
(4)若S△ACP=S△ACD,求点P的坐标。
这道题难度分为四个层次。第一问,求二次函数的解析式,是解后面三道题的基础;第二问,求二次函数中静态面积,这里还设置了两个小问,先问特殊位置三角形面积的求法,再问一般位置三角形面积的求法,第二小问是要掌握作辅助线的基本技能转化为第一小问来解决,体现了从特殊到一般的基本思想;第三问,动态三角形面积最值问题,是在第二问基础上继续拓展,需要学生掌握函数思想、转化思想才能解决本题;第四问还涉及了方程思想。本题前三问是必做题,时间20分钟,是为绝大多数学生设计的,选择了层层递进的二次函数数形结合的作业,以培养学生数形结合思想,积累必要的数学知识、提升基本的解题技能;最后一问为选做题,为学优生提高解决二次函数动点题型作业的能力,以培育学生抽象函数思维,为高中阶段学习打下坚实基础。
3.完善分层作业评价,增强作业导向性
完善分层作业评价、增强作业分层评价的导向性,有助于在针对每一层级的学生实施科学、合理评价目标的同时,引导学生自主学习,在完成教师布置的作业的基础上,逐步提升个体的学习能力、知识应用能力以及创新创造能力。
作业是教师与学生沟通的最有效的路径之一,学生通过做作业可以检验自己对课堂所学知识的掌握情况,便于他们在接下来的课堂学习中有重点、有目的地去听课、去跟老师沟通;教师通过批阅学生的作业,可以比较全面地掌握每位学生对课堂所学知识的识记、理解以及应用的熟练程度,适当降低分层作业量化指标的评价,更加关注分层作业感性评价指标的运用,针对不同层级的学生实施差异化评价,增强分层作业评价鼓励的功能作用,能够帮助学生针对自己的知识缺陷来进行针对性强化,作业设计就必然会达到事半功倍的效果。以“矩形、菱形与正方形”模块知识教学为例,对于折叠等难度较大的作业,教师应该以定性评价为主,比如重点关注学生在解这类题目过程中,运用到了哪些数学知识、哪一个环节遇到了问题,而不是简单地看看学生的解题结果是否正确;而对于难度较低的习题,则应该适当增加定量评价的占比,以结果为导向,剖析学生哪些基础知识掌握不牢固、基本技能水平有待提升等,久而久之,整个班级学生的数学成绩就会大幅提升,数学核心素养培育目标也必将会尽快实现。
综上所述,初中数学教学需要结合政策规定和课程改革的要求,结合数学作业设计原则与逻辑,针对性地改进与优化作业设计思路和内容,通过积极有效的调整和改变满足学生的发展需要。从课程教育理念而言,教师应当提供针对性的教学设计,在设计期间本着作业层次性、弹性化和个性化原则,使学生能满足自主性的学习与发展需求,从而提高初中数学作业设计质量,进而提高初中数学综合教学质量。
【参考文献】
[1]明月.基于“四基”的高中立体几何教学设计研究[D].牡丹江:牡丹江师范学院,2022.
[2]杜瑛.培养“四基”和“四能”的教学实践与思考—对《直线的方向向量与平面的法向量》的教学评析[J].数学之友,2021(03).

