巧用分段放缩法证明函数不等式
⦿ 广东省广州市华南师范大学附属中学 周建锋
1 问题的提出
函数不等式的证明一直是中学数学中的一个热点,证明函数不等式,可以将其转化为求函数最值的问题,通过求导,划分单调区间,找出最值.但新的高考改革越来越关注学生的数学核心素养,对学生分析问题、解决问题的能力提出了更高的要求,因此建立在通性通法基础上的应变能力尤为重要.
放缩法作为一种重要的证明不等式的方法被广泛应用,包括寻找中间常量、切线放缩、割线放缩、利用泰勒展开式放缩等.放缩法最大的难点在于放缩的尺度,因为放缩法的理论基础是不等式的传递性,如a>b,b>c⟹a>c.这是一条“单行道”,一旦尺度过大 “放过头”,如a>b,b
2 分段放缩法的原理
将分段放缩的策略运用到函数不等式的证明中,在区间(a,b)上证明形如f(x)≥g(x)的不等式,有时可以通过恒等变形,构造出等价的函数不等式F(x)≥G(x),且F(x)≥m(x)(m(x)也可以是常数),M(x)≥G(x)(M(x)也可以是常数),若有m(x)≥M(x),则F(x)≥G(x),故f(x)≥g(x)成立.但在区间(a,b)上不一定能满足m(x)≥M(x),此时将(a,b)划分为若干个子区间(a1,a2]∪(a2,a3]∪……∪(an,an+1)(其中a1=a,an+1=b),在每一个子区间(ak,ak+1](k=1,2,……,n,k=n时区间为开区间)上有F(x)≥mk(x)≥Mk(x)≥G(x),则在(a,b)上必有F(x)≥G(x),即f(x)≥g(x).
分段放缩的优点在于通过缩小区间,把放缩的尺度缩小,可以很好地避免“放过头”的问题.在实施过程中,寻找子区间的分界点是关键.
3 分段放缩法的应用
3.1 在寻找中间常量中采用分段放缩

(1)求n的值;

分析:(1)过程略,答案为n=-1.



当0
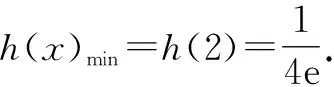
这条路径是否无法证明呢?重新反思,能否把区间(0,+∞)进行分段,从而解决放缩过度的问题呢?
(1)首先注意到h(x)>0,所以当0 仍以例1为例,证明ex-3>x(lnx-1). 分析:如图1,由图象可以预判,y=ex-3图象上任一点的切线均不可能全在y=x(lnx-1)的图象上方,所以不可能在(0,+∞)上对y=ex-3运用切线放缩. 图1 综上可知,ex-3>x(lnx-1). 反思:与第一种证法不同,这种证法利用切线或泰勒展开式,对指数函数进行适当放缩,但仍会遇到在整个区间(0,+∞)上不能直接证明的情况.利用分段放缩,在不同子区间上选用不同的放缩方法,提高了证明的灵活度. 所以f′(x)<0. 数学的乐趣在于不断探索,推陈出新.在证明某些函数不等式(如指数函数、对数函数与三角函数中至少两类混杂在一起的函数不等式)时,直接用求导的方法证明往往比较困难,通常考虑利用放缩法证明.而分段放缩法可以更精确地解决放缩尺度的问题,在需要运用放缩法的时候不妨结合分段放缩法,这样易于攻破难点,体会数学的美妙,在数学的世界里快乐地翱翔!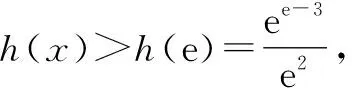


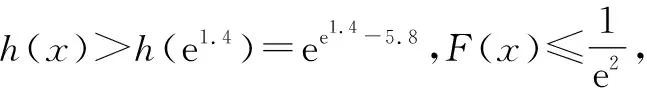

3.2 在切线放缩证明中采用分段放缩

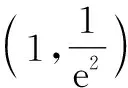




3.3 在割线放缩证明中采用分段放缩





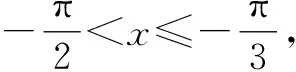
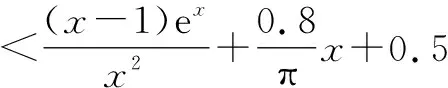


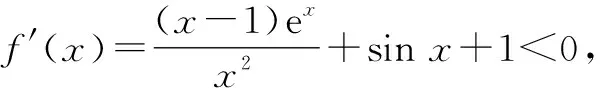
4 结束语

