假以时间 给你惊喜——一节高三复习课的教学尝试

⦿ 四川省双流中学 王保弟 杜江涛

1 教学内容分析

1.1 内容分析

本节课是由学生作业中的一道大题出发,追溯题目背景,是人教A版普通高中课程标准试验教科书数学2-1(选修)第73页A组第6题,第81页B组第3题.

通过圆锥曲线知识的学习,发现解决解析几何问题的通法——坐标法,偏重于相关量的数量关系的研究,由于代数运算复杂,对运算能力要求较高,往往使很多学生对解析几何望而生畏.事实上,解析几何问题的本质仍是几何问题,若能充分把握解析几何中图形的特征,挖掘图形的相应几何性质,恰当地运用平面几何的相关知识求解,往往能简化运算,优化解题过程.

1.2 学情分析

本节课之前,学生在必修二第三章圆的知识的基础上,学习了圆锥曲线,有一定的类比转化与分析问题的能力,以及代数运算能力.学生思维活跃,求知欲强.但面对繁难的代数运算,学生难免会有畏难情绪,所以挖掘试题背后的有关几何性质是关键.这需要熟练掌握一些常见的平面几何图形的性质,而此挖掘过程仍需要教师重点指导.通过“一题一课”微专题的形式,以点带面,聚焦关键内容,帮助学生感悟数学思想方法,实现从“解题”到“解决问题”的转变.

1.3 学习目标

(1)回顾三角形内角平分线定理,感受解圆锥曲线题目的方法,即坐标法和几何法;

(2)利用不同的设点、设直线的方式解决圆锥曲线问题,探索并感悟外角平分线定理的妙用;

(3)在解决典例的过程中,总结解决问题的方法和技巧,并能用外角平分线性质快速得到变式问题的答案.

1.4 评价目标

(1)通过课前自测(要求学生自主完成),感受解析几何通法(坐标法)与解析结合本质(几何法).

(2)通过典例分析,探究不同的设点、设线方式带来的不同解题方法,并通过几何背景的挖掘感悟几何法在解题中对计算的简化作用.

(3)通过运算化简,提升运算能力;通过挖掘几何性质,体会数形结合的思想.

2 课堂实录

环节1：课前自测,做好铺垫.

师:老师在课前已经布置了学习任务,接下来通过投影仪一起分享大家的学习成果.

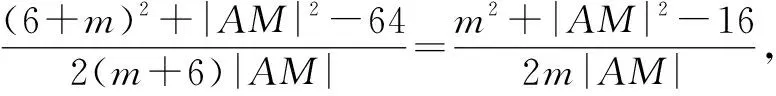
生4:由题意,得|F1M|=8,|F2M|=4.

又||AF1|-|AF2||=2a=6,所以|AF2|=6.

师:非常棒!同学们利用角平分线性质和双曲线定义解得此题,感受了圆锥曲线问题可以一题多解,选择不同方法,有不同的解题感悟.

设计意图：设置课前自测环节,目的是帮助学生体会解析几何问题的解决途径即坐标法和几何法,而本题多种解法中,以利用三角形内角平分线定理最为简单,说明在解答解析几何问题时要注意运用平面几何知识,使问题获得简单解法,也为今天的学习作铺垫.

环节2：对比方法,突破难点.

例题如图1,已知抛物线C:y2=4x的焦点是F,准线为l,已知点P(9,6),若过点F的直线交抛物线于不同两点A,B(均与点P不重合),直线PA,PB分别交l于点M,N,求证:MF⊥NF.

图1

师:请同学们先尝试解答,然后再分享解法.

(8分钟后,大多数同学能用一种方法规范解答,用投影仪展示学生解法.)

当直线AB斜率存在时,设直线AB的方程为y=k(x-1),A(x1,y1),B(x2,y2).

由韦达定理,得

①

师:请这位同学分享一下求解思路和过程.

生1:设直线的点斜式方程,得到向量数量积关于参数k的表达式,最后通过代数运算发现两个向量的数量积为零,从而证得结论.

师:非常棒!还有其他同学愿意分享不同的解题方法吗?

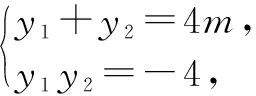
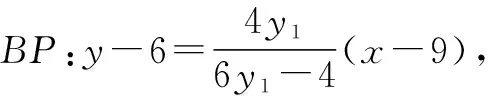
师:非常巧妙!这种方法优化了第一个同学的计算过程,还有同学愿意分享吗?

生3:在抛物线y2=4x中,准线l:x=-1,焦点F(1,0).

师:非常好!这位同学与生2的不同点是利用数量积为零证明了结论,还有不同方法吗?

对于lAP与lBP1,分别令x=-1,可得

要使MF⊥NF,则MQ2=FQ2,即

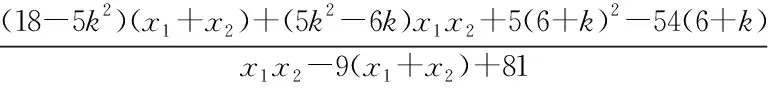
因为Q为MN的中点,QM=QN=QF,所以M,F,N在以Q为原心的圆上,故MF⊥NF.

生4:前三位同学通过数量积为零或斜率之积为-1证得结论,我通过三点共圆来证明.

师:这位同学思路很清晰,利用圆周角证明垂直,但美中不足的是忘记对斜率不存在这种特殊情况的讨论了.

生5:老师,我还有一种不同的解法.

师:请分享一下你的解题思路.

生5:如图2,设A,P在准线上的射影分别为A′,P′.

图2

连接AA′,PP′,则AA′⊥l,PP′⊥l,于是AA′∥PP′.

易得△AMA′∽△PMP′.

由三角形外角平分线定理的逆定理,可得FM平分∠AFP的外角.连接PF,并延长交l于点G,可得FM平分∠AFG.

同理可得,FN平分∠BFG.

又∠AFG+∠BFG=180°,所以2(∠MFG+∠NFG)=180°,因此∠MFG+∠NFG=90°,即∠MFN=90°,故MF⊥NF.

师:非常厉害!这位同学所用思路与前4位同学有所不同,他从几何图形出发,利用几何关系证得结论.利用数形结合的思想方法,简化计算,优化解题过程.

师生:师生共同感悟总结.

思维导图如图3所示:

图3

师:上述例题的求解过程表明,坐标法会导致圆锥曲线问题求解复杂,运算量较大.但是,通过深入探索和挖掘圆锥曲线的几何性质,则能巧妙求解问题.由学生5的启发得到下面结论,请同学们课后探究.

引理:若圆锥曲线C的离心率为e,焦点F所对应的准线为l,曲线C的弦AB所在的直线交准线l于点P;当点P在弦AB内时,FP平分∠AFB;当点P在弦AB外时,FP平分∠AFB的外角[1].

设计意图：通过自主探究,学生分享交流,师生一起探究典例的解法,充分发挥学生的主观能动性,体现学生的主体地位,引导学生从不同的角度认识问题,实现一题多解,培养学生发散思维的能力,提升学生分析问题、解决问题的能力,同时在学生分享过程中锻炼他们的语言表达能力.

环节3：类比迁移,感悟思想.

根据以上条件,我们还可以研究哪些问题?写下你想研究的问题并思考如何解决.

变式1已知点P(9,-6),求证:MF⊥NF.

变式2已知点P(6,3),求证:MF⊥NF.

变式3已知点P(0,0),求证:MF⊥NF.

变式4已知点P(x0,y0),求证:MF⊥NF.

变式5C:y2=2px(p>0),求证:MF⊥NF.

变式6以MN为直径的圆,是否经过定点?若是,请找出定点;若不是,请说明理由.

设计意图：设置变式训练的目的,是让学生现学现用,通过方法的选择提升解题能力,促进学生对知识和方法的迁移,通过“一题多解”再到“多题一解”,使学生实现从解题到解决问题的提升.

环节4：深化拓展,形成模型.

推广:已知抛物线C:y2=2px(p>0)的焦点是F,准线为l,已知点P(x0,y0),若过点F的直线交抛物线于不同两点A,B(均与点P不重合),直线PA,PB分别交l于M,N,求证:MF⊥NF.

师:我们用几何画板演示上述结论.

师:在抛物线中有这样优美的平面几何性质,那在椭圆、双曲线中此结论是否也成立?请同学们课后探索.

设计意图：通过例题教学,学生从不同的角度思考获得不同的解法,也复习了不同的知识点,真是“横看成岭侧成峰”.通过比较不同解法计算量的大小,发现解答这类问题的通法与妙法,为后续优化算法积累经验.通过“一题多变”对某个问题进行多层次、多角度、多方位的探索.培养学生发散思维,是学生创新思维的必备前提.此题不仅锻炼了学生用类比的方法进行思考和学习,而且使学生对解决问题的思路理解得更透彻.每问一变都层层递进,步步深入,环环相扣的密切联系.同样可以从一种研究对象的结论出发,通过类比得出另一种研究对象的许多意想不到的结论.创造的喜悦难以想象.

环节5：归纳小结,课外拓展.

本课从一道解析几何题目出发,探究并分享了各种不同的解题方法,最容易想到的是通法——设点、设线,但同样是设线也有讲究,不同的设法计算量有差异;利用平面几何结论可获得简捷解法.

课后作业:(限于篇幅题目略去.)

3 教学反思

这节课以教师为主导、学生为主体、问题为主轴、练习为主线,以“一题一课”的形式,让学生自主探究例题的解法,其中渗透了数形结合、化归转化、分类讨论等数学思想,提升了学生解答圆锥曲线问题的能力.在专题复习中,实现了知识结构化、方法系统化、思想实质化[2].

在教学活动中,先让学生独立思考,再自主探究,体会方法,相互分享,给予学生充分的时间去探究、思考、表达,使学生经历和体验解决问题的全过程,感悟通法与妙法.通过一题多解、多题一解,实现“做一题,得一法,会一类,通一片”,实现从“解题”到“解决问题”.

但本节课仍然留有遗憾,为了让学生更直观地感受随着点P的运动,结论依然没有发生变化,我们都是用几何法证得结论,并用几何画板演示结论,没有充足的时间让学生感受利用通法——坐标法来证明,后续还需通过坐标法提高学生的数学运算能力.

小结只强调了知识方面,对育人方面做得不到位,课后总结一首打油诗:

一题多解思维阔,学生主体来开拓,

一题多变问题活,定能扩展有收获.

解析几何形态多,开动脑筋去探索,

想要数学学得好,自我学习不能少!

如果能在课堂上这样小结,文化氛围更浓,教学效果和育人效果会更好,以后会不断改进,自觉做到教书育人.