地铁循环荷载下黏土污染圆砾的大型动三轴试验及动力特性研究

马少坤, 田发派, 黄海均, 张加兵, 段智博, 龚 健

(1.广西大学 土木建筑工程学院,南宁 530004;2.广西大学 工程防灾与结构安全重点实验室,南宁 530004;3.清华大学 土木水利学院,北京 100084)

随着我国基础设施建设的蓬勃发展,大部分城市正兴建地铁盾构隧道,其中穿越圆砾层及黏土-圆砾复合地层极为常见,如我国华北地区的北京,华南地区的深圳、广州和南宁以及西南地区的重庆和成都等城市。在地铁盾构隧道的修建以及运营过程中,地铁基床层的圆砾极易被泥浆泵送,黏土随水渗流作用的侵入,内部结构的翻浆等导致的黏土所污染。受污染的圆砾细料含量将增多,其内部结构、强度、刚度、变形及渗透特性将发生明显变化[1-4],最终导致整个地铁路基结构的服役性能大幅度劣化,严重威胁到地铁的运行安全。因此掌握受污染圆砾在地铁循环荷载作用下的动力特性及累积塑性应变的演化特征是十分必要的。

动三轴试验是研究材料动力特性的有效手段[5-8],近年来,许多学者利用动三轴对污染粗粒土开展了大量的研究,并取得了丰硕的成果,如吴琪等[9]通过开展不排水动三轴试验,研究了细粒含量对细粒-砂粒-砾粒混合料动强度的影响,结果得到随着细粒含量的增加,试样的动强度呈现先降低后增加的趋势。王家全等[10]利用GDS动三轴进行了一系列饱和砂砾的动三轴试验,研究了不同细粒含量下砂砾的动力特性,发现试样的累积应变随着细粒含量的增加不断增大,而回弹模量随之减小。杨志浩等[11]对重载铁路路基上不同污染程度的碎石进行了一系列动态三轴试验,试验得到随着污染细颗粒含量的增加,试样的累积塑性应变近似线性增加。Khogali等[12]通过试验得到,循环荷载作用下,粗粒土的轴向应变随着污染细料含量的增加而减小,而其回弹模量随着污染细料含量的增加而增加。Budiono等[13]研究了煤尘污染对道砟永久沉降和弹性应变的影响,结果得到随着煤尘含量的增加,道砟的塑性沉降速率增加,其弹性和重装刚度增加速率降低。Duong等[14]通过对三种含水量和四种细粒含量下制备的道砟试样进行循环三轴试验,发现试样在饱和状态下,细粒含量越高,永久轴向变形越大,而在低含量情况下,发现该趋势相反。Tennakoon等[15]对不同污染程度的道砟进行了一系列的大型排水循环三轴试验,结果发现试样的轴向应变和体积应变随污染细料含量的增加而增加。Ebrahimi等[16]通过大型循环三轴试验,在模拟交通荷载作用下,测定了不同细料污染条件下铁路道砟的塑性应变,结果表明污染细料含量的增加将加大道砟的累积塑性应变。Cao等[17]利用大型动三轴仪,对不同污染细料含量的凝灰岩进行了一系列固结排水三轴循环试验,试验结果表明,随着污染细料含量增加,试样的累积轴向应变和体应变增加呈现先增加后减小的趋势。可见,污染后的粗颗粒填料在长期循环荷载作用下的累积塑性应变演变规律仍未得到共识,且上述研究污染粗颗粒填料大多为污染道砟填料。同时,目前对地铁荷载作用下铁路路基污染圆砾的动力特性及累积塑性应变演化规律的研究鲜有报道,有待开展进一步研究。

综上所述,本文以黏土污染的圆砾为研究对象,利用GDS大型三轴循环试验系统,开展了一系列饱和不排水动三轴试验。探究了不同围压及动应力幅值下黏土污染水平对圆砾长期动力特性的影响。所得试验成果可为地铁路基结构设计及其工后沉降预估提供参考。

1 试样和试验方法

1.1 试验仪器及用土

试验仪器采用粗粒土GDS大型三轴循环试验系统(DYNTTS),如图1所示。该系统主要包括轴向加载系统、压力罩、围压/反压控制器、孔隙水压力传感器、数据采集系统等。该系统允许施加最大围压1.0 MPa,最大轴向应力60 kN,最大加载频率2 Hz,最大轴向行程75 mm。

图1 DYNTTS大型三轴循环试验系统Fig.1 DYNTTS large triaxial cyclic test system

试验所用圆砾及模拟污染的黏土均取自于南宁地铁施工现场,取样位置及土样如图2所示。

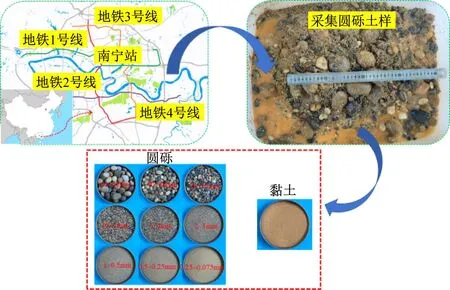
图2 取样位置及土样Fig.2 Sampling location and soil sample

圆砾级配参照前期所做研究进行选取[18],而黏土的级配则根据TB 10102—2010《铁路工程土工试验规程》[19],采用筛析法和激光粒度分析仪联合对其进行了测量。圆砾及所掺污染黏土的颗粒级配曲线如图3所示。圆砾及所掺黏土的基本物理参数如表1所示。

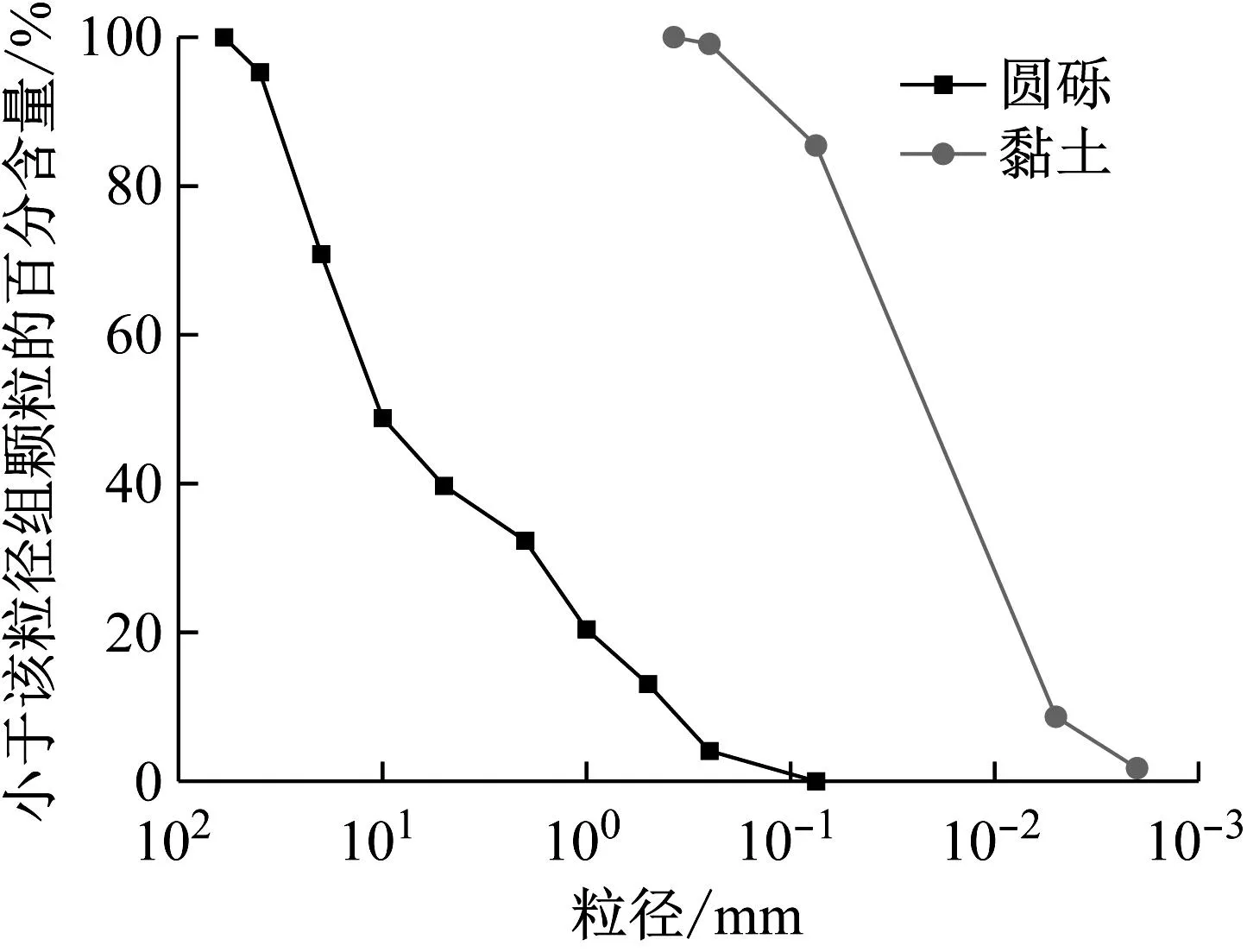
图3 圆砾和黏土的级配曲线Fig.3 Gradation curves of round gravel and clay

表1 圆砾及黏土的基本物理参数Tab.1 Basic physical parameters of round gravels and clays

目前常用的污垢指数为污损百分比(fouling index,FI)和孔隙污染指数(黏土污染水平)(clay flouling level,VCI)。针对污损百分比FI,Indraratna等表示FI不能准确估算污染物的体积,提出采用VCI对污染程度进行量化。因此,为准确地分析圆砾所受黏土污染的程度,本文采用VCI对其所受污染程度进行量化,该指标已被诸多研究人员所采用[20-22]。VCI的定义为污染物(黏土)体积占圆砾孔隙体积的比率,其表达式如下

(1)

式中:Vf为黏土的实际体积;Vvb为圆砾孔隙的体积。

对式(1)的土体参数进行如下换算,可得式(2)

(2)

式中:Vvb,Vsb,eb,Gsb和Mb分别为干净圆砾的孔隙体积、固体颗粒体积、孔隙比、比重和干的质量;Vvf,Vsf,ef,Gfb和Mf分别为污染黏土的孔隙体积、固体颗粒体积、孔隙比、比重和干的质量。上述参数具体取值见表1。

1.2 试验方案

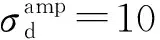
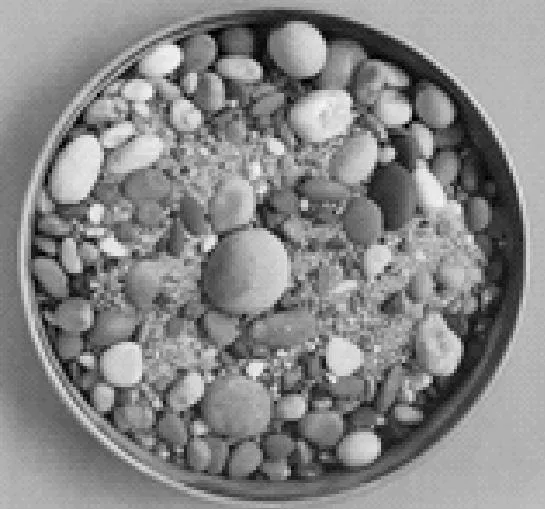
VCI=0

VCI=20%

VCI=30%

VCI=40%

VCI=60%图4 不同VCI试样Fig.4 Specimens of different VCI

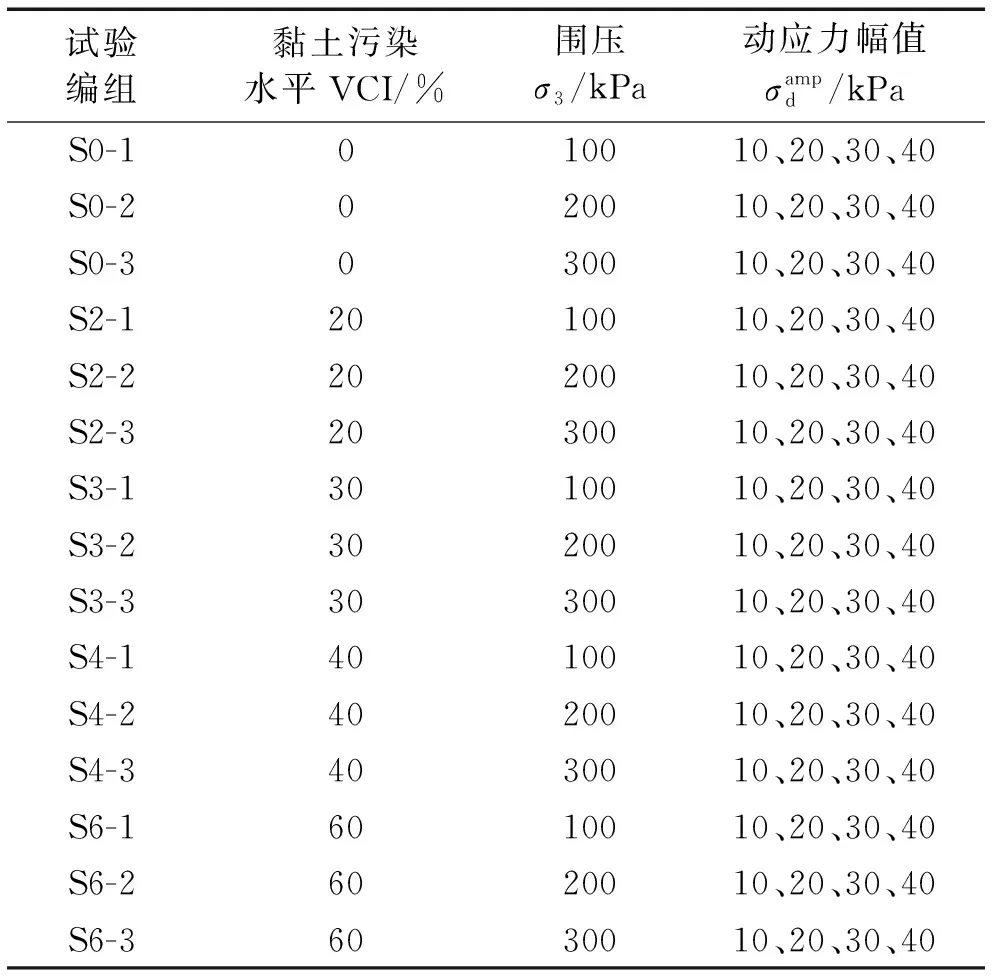
表2 动三轴试验方案Tab.2 Dynamic triaxial test scheme

1.3 试验加载条件设置

考虑到地铁荷载作用具有瞬时性,且地铁隧道埋藏较深,故试验采用固结不排水条件。试验中采用正弦波来模拟实际运营条件下列车动荷载对路基的作用[25],如图5所示。为降低试验工作量及减少由不同试样间差异引起的结果偏差,本试验采用多级加载法对试样进行加载,该方法在动力试验中已被广泛采用[26-28]。每级动应力幅值下振动次数设定为10 000次。加载频率按照Indraratna论文中[29-30]公式f=v/L计算,南宁地铁时速取v=72 km/h,地铁每节车厢长L=20 m,计算得加载频率为1 Hz。

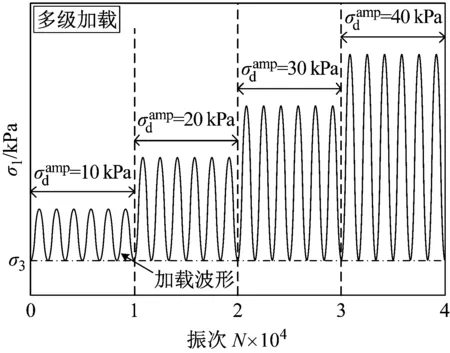
图5 加载波形Fig.5 Loading waveform

1.4 试验过程

砾类土的原状土样较难取得及保存,所以本文试样均采用重塑土样。按照TB 10102—2010《铁路工程土工试验规程》的要求,试样采用分层振捣法制备,共分10层,即首先根据圆砾相对密度(本文Dr=0.5)、VCI公式及试验方案分别计算和称取每层圆砾、黏土质量,搅拌均匀,而后分层击实至相应高度,最终制成直径为300 mm,高度为600 mm的试样。试样制备完毕后从仪器底部充入3 h二氧化碳,然后通入12 h无气水以溶解试样内部二氧化碳,最后采用分级加压的方式对试样进行反压饱和,反压共分4级,每级增加50 kPa并维持4 h,最后1级反压增至200 kPa。饱和结束后,若孔压系数B值大于0.95,说明试样基本饱和,方可对试样进行加载。整个试验过程如图6所示。

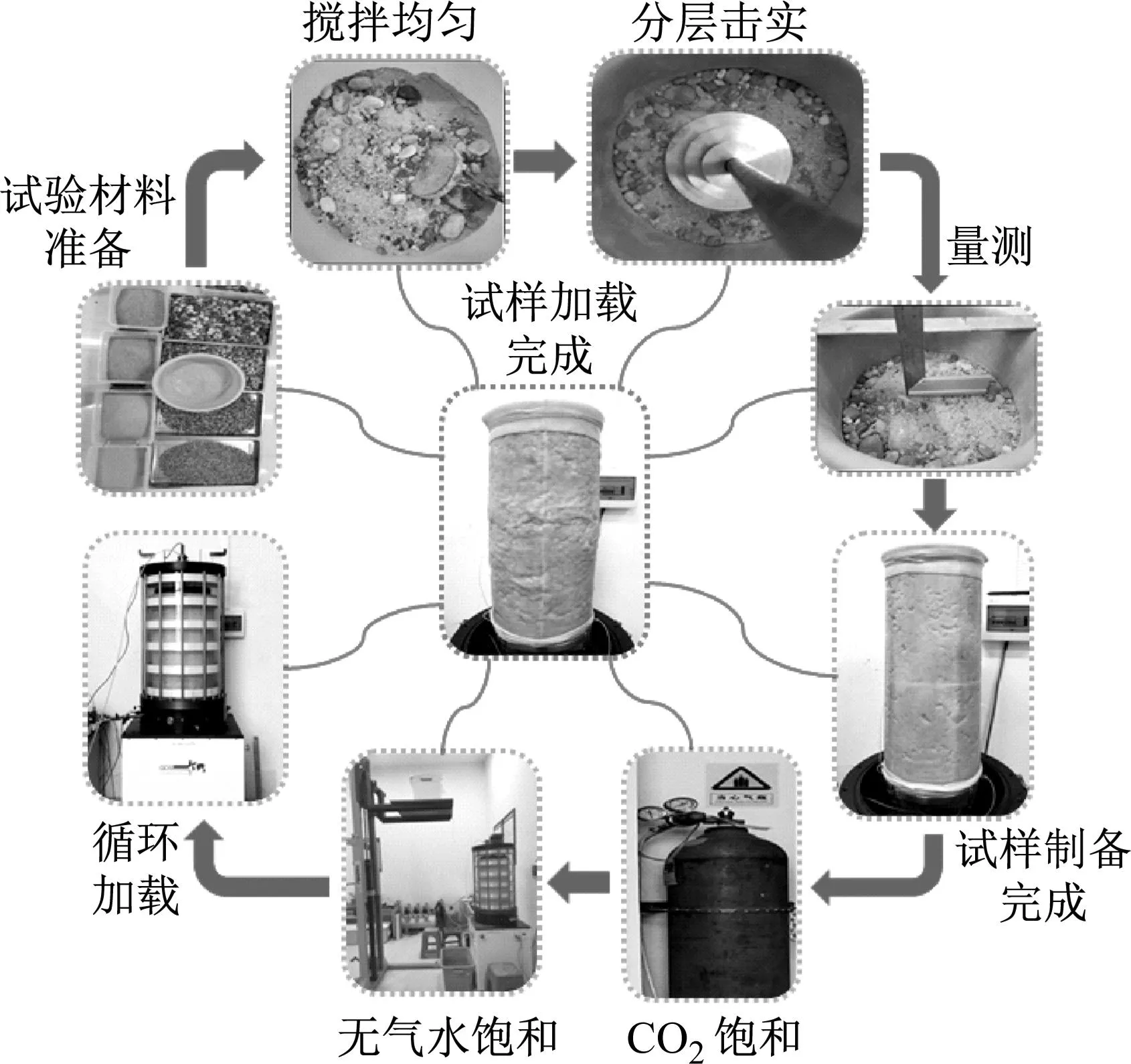
图6 试验过程图Fig.6 Test process illustration

2 试验结果与分析

2.1 累积塑性应变

循环荷载作用下,VCI=0%,σ3=100 kPa试样在不同动应力幅值下的轴向应变时程曲线如图7所示。从图7可以看出,试样的轴向应变ε1是由可恢复的弹性应变εe和不可恢复的塑性应变εp组成。在循环荷载作用下,轴向应变呈现周期性变化。

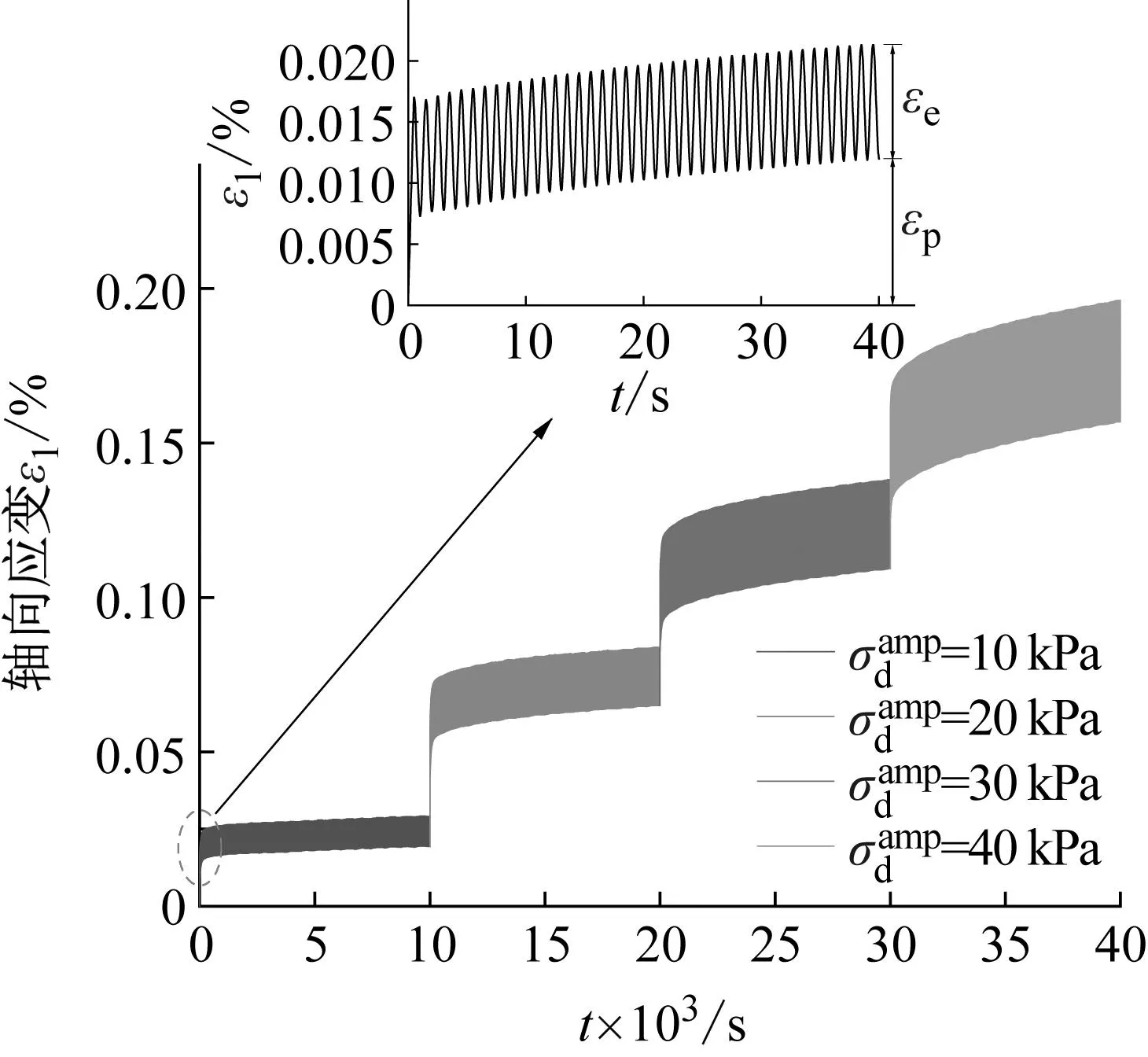
图7 循环荷载下轴向应变随加载时间的变化曲线Fig.7 Variation curves of axial strain with loading time under cyclic loading

地铁循环荷载作用下,不同黏土污染水平、围压及动应力幅值条件下污染圆砾的轴向累积塑性应变εp与加载次数N之间的关系曲线,如图8所示。

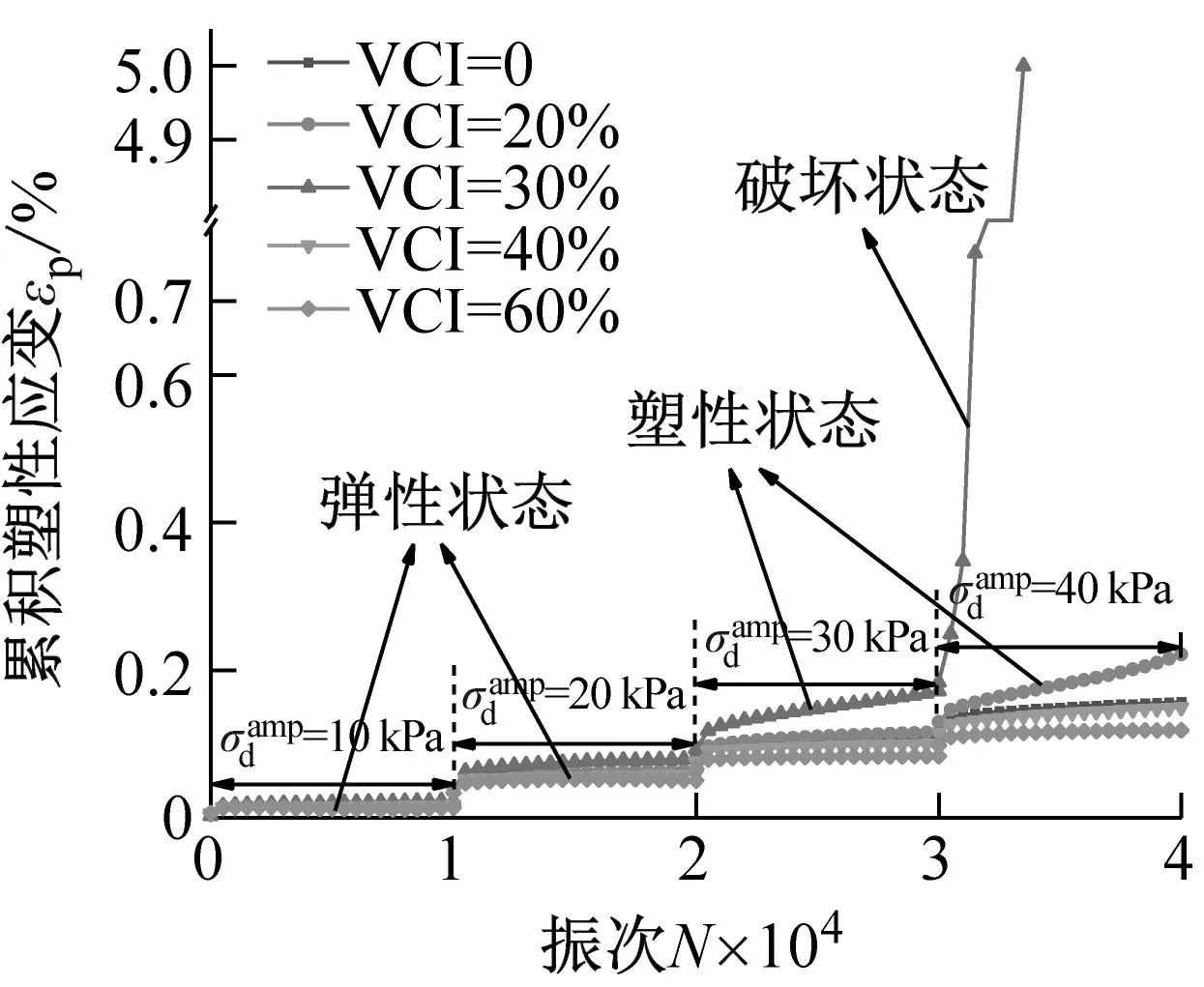
(a) σ3=100 kPa

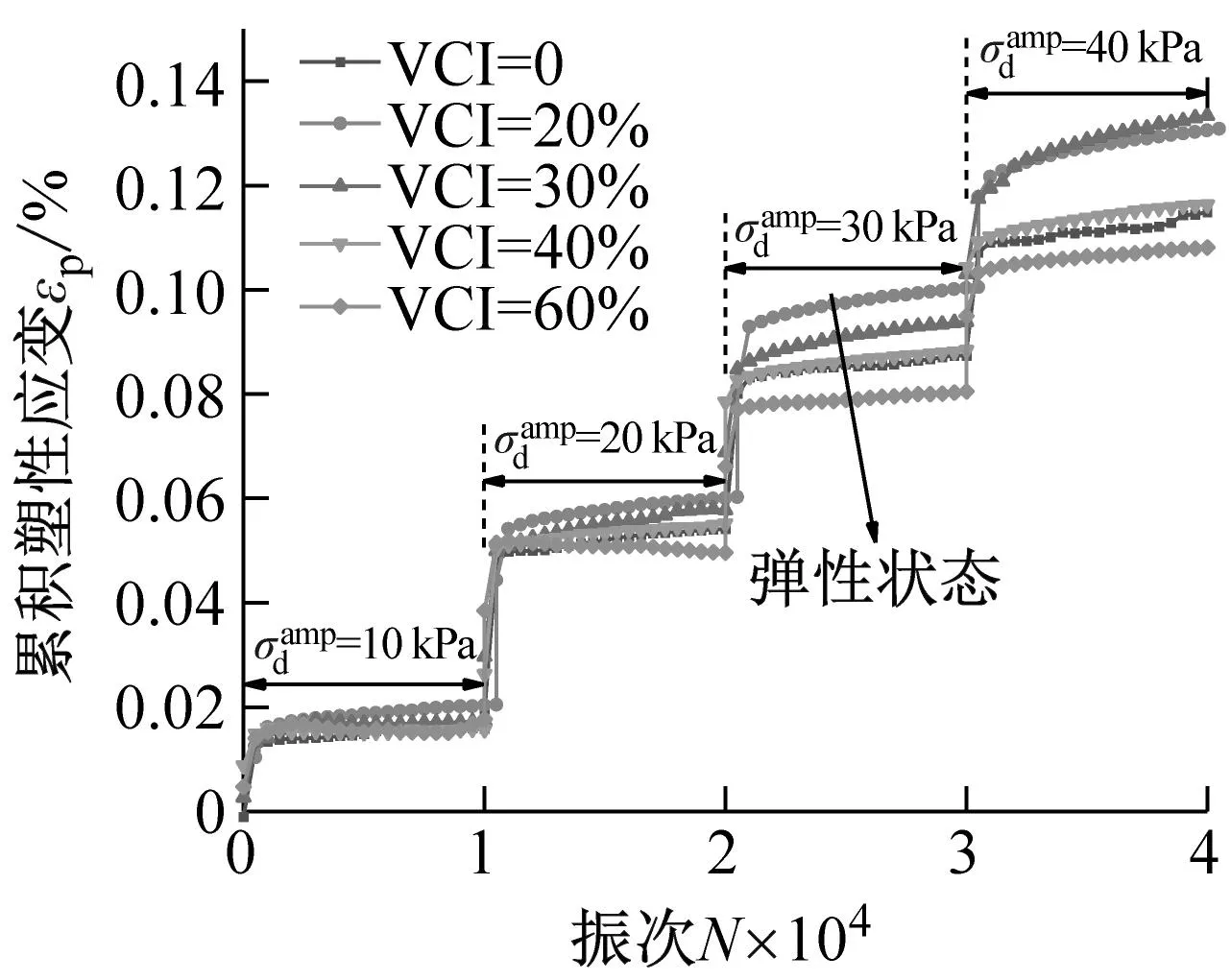
(b) σ3=200 kPa

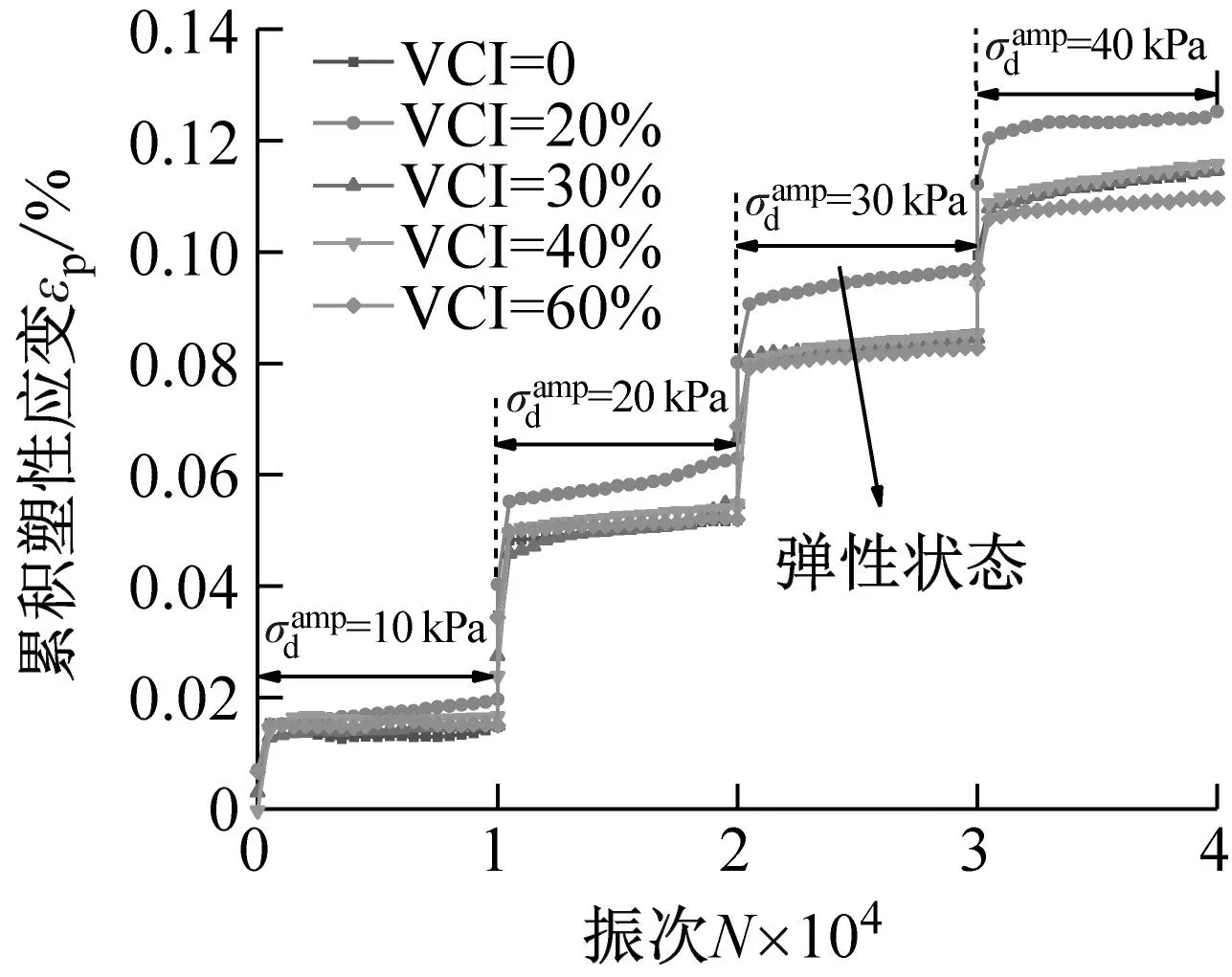
(c) σ3=300 kPa图8 污染圆砾的累积塑性应变εp与加载次数N之间的关系曲线Fig.8 The relationship curve between the accumulated plastic strain εp and the number of loading N for the fouled round gravel

对于较高围压σ3=200 kPa及σ3=300 kPa,在各级动应力幅值下,5种VCI指标试样的累积塑性应变几乎均表现为在加载初始阶段快速增加,随后逐渐变缓直至相对稳定,这主要是由于高围压限制了试样内部颗粒间的滑移,提高了试样承受外荷载的能力。此外,通过对比可知,高围压(σ3=200 kPa、300 kPa)下试样的累积塑性应变明显小于低围压(σ3=100 kPa)下试样的累积塑性应变。由上述分析可得,对于埋深较深的地铁隧道,列车的运行是相对安全的,不需要对圆砾路基进行处理。另外,从图中可知,不同围压及动应力幅值下,VCI=20%、30%试样的累积塑性应变是明显大于VCI=0%、40%、60%试样的累积塑性应变,这表明黏土污染水平对圆砾的累积塑性应变有显著的影响。

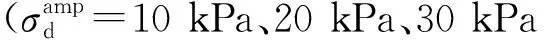
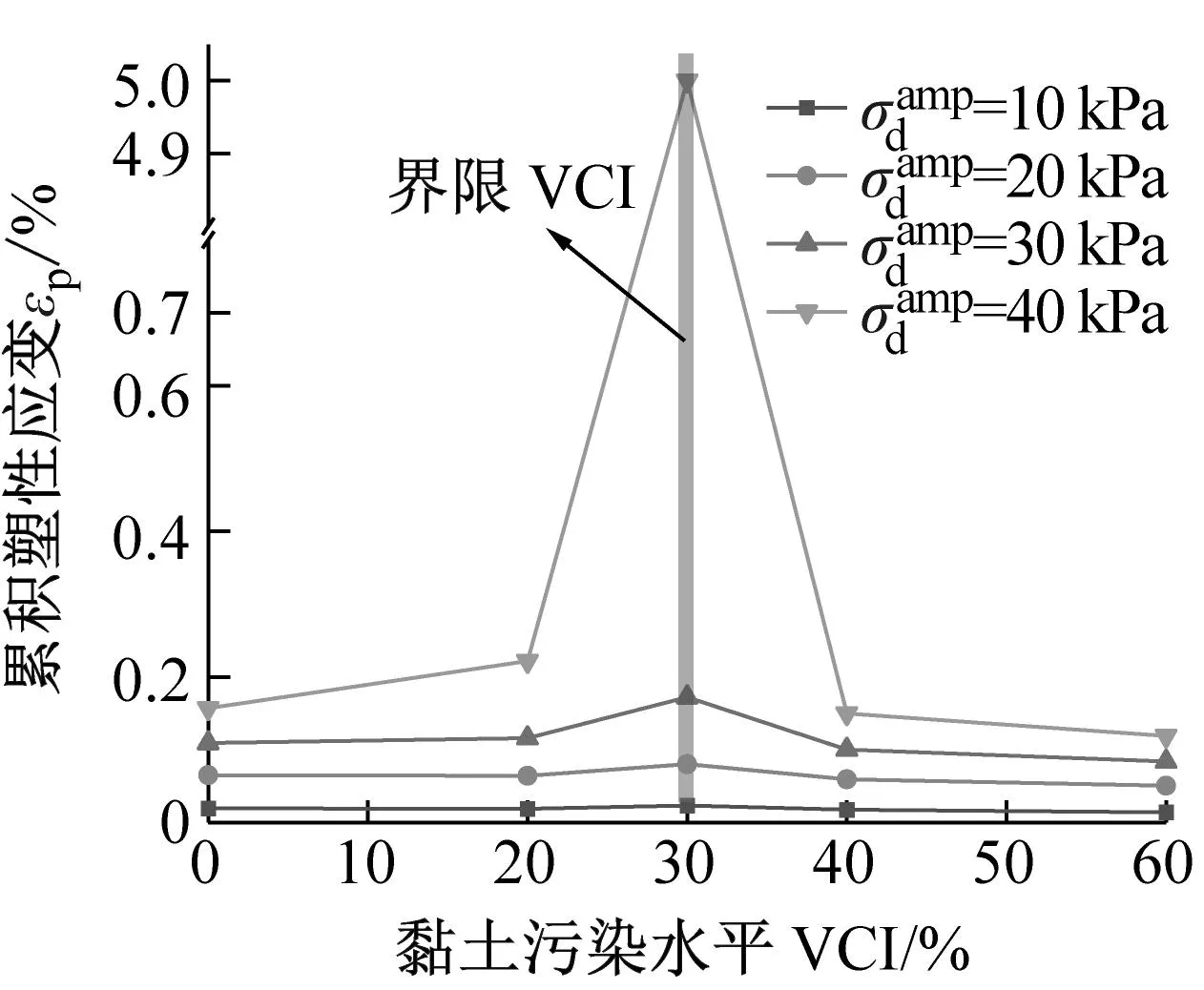
(a) σ3=100 kPa

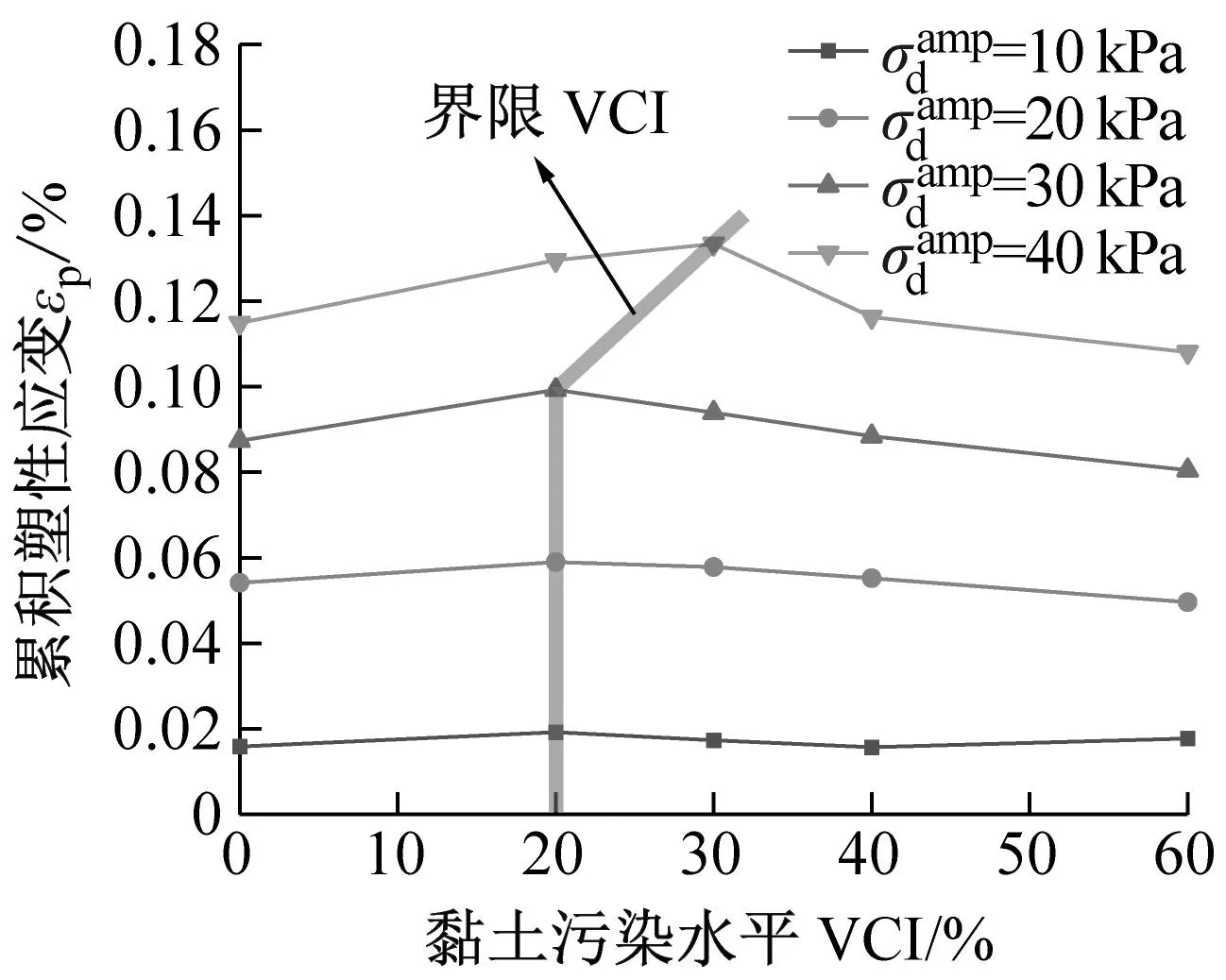
(b) σ3=200 kPa

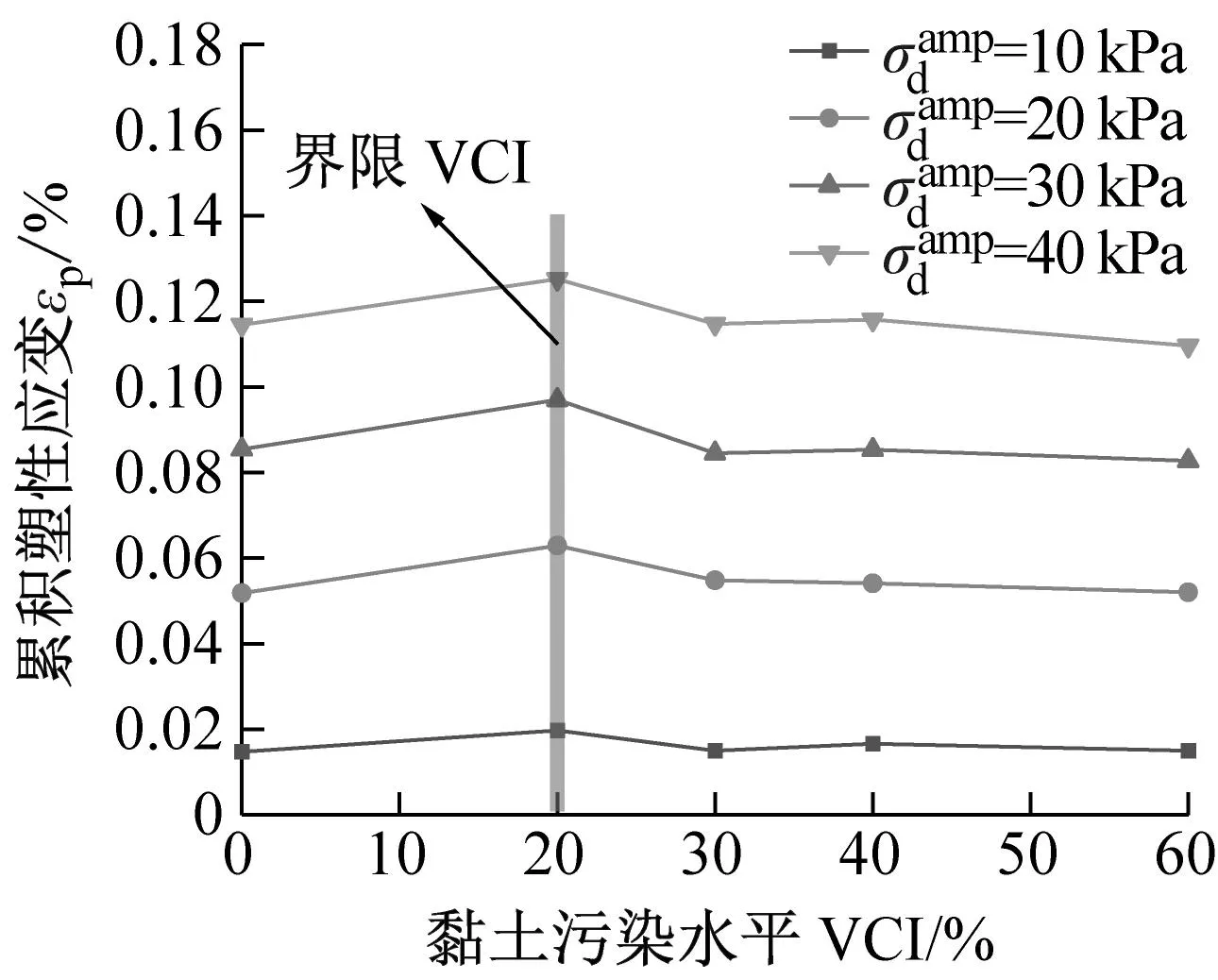
(c) σ3=300 kPa图9 各个加载阶段污染圆砾的最终累积塑性应变εp与黏土污染水平VCI之间的关系曲线Fig.9 The relationship curve between the final cumulative plastic strain εp and the clay fouling level VCI of the fouled round gravel at each loading stage

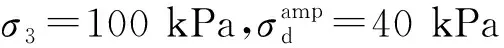
2.2 弹性应变

循环荷载作用下,不同黏土污染水平、围压及动应力幅值条件下污染圆砾的弹性应变εe与加载次数N之间的关系曲线,如图10所示。

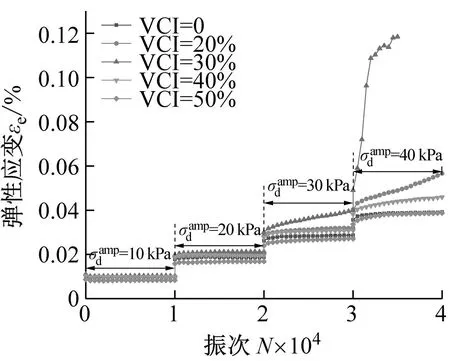
(a) σ3=100 kPa

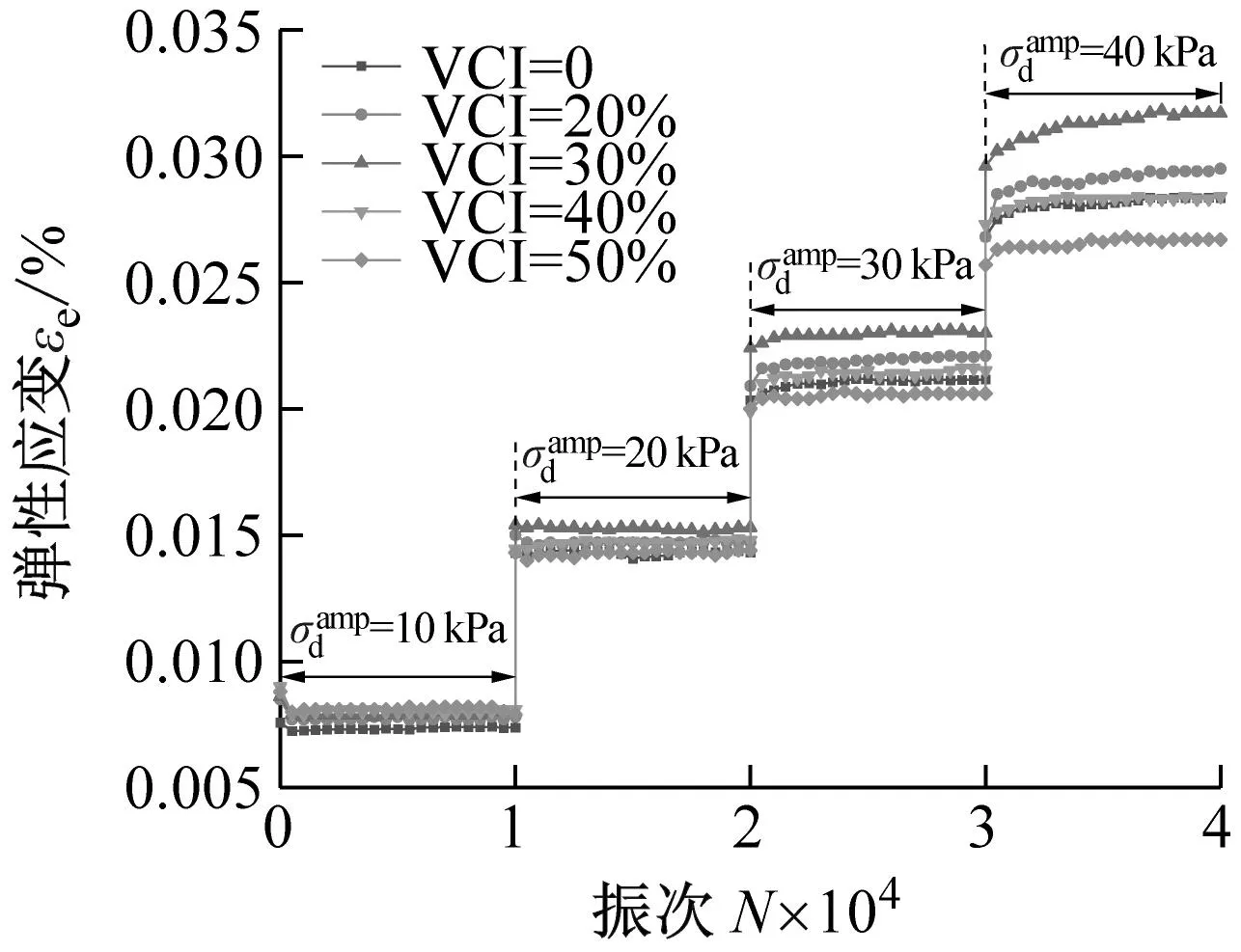
(b) σ3=200 kPa

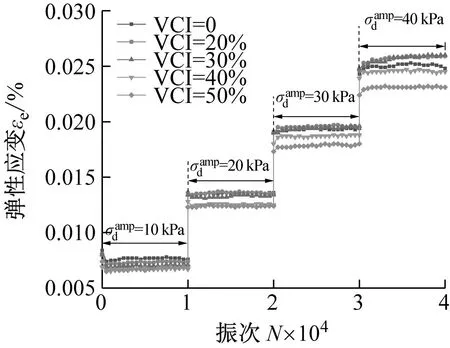
(c) σ3=300 kPa图10 污染圆砾的弹性应变εe与加载次数N之间的关系曲线Fig.10 The relationship curve between the elastic strain εe of the fouled round gravel and the number of loading N

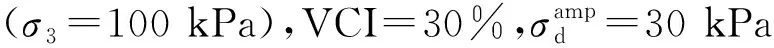
2.3 滞回曲线

试样VCI=0%,σ3=100 kPa在不同动应力幅值下的滞回曲线如图11所示。从图11可以大致看出,在动应力作用下,滞回曲线的初始间隔较大,而后趋于密集,试样的动应变增长缓慢甚至停止增长。

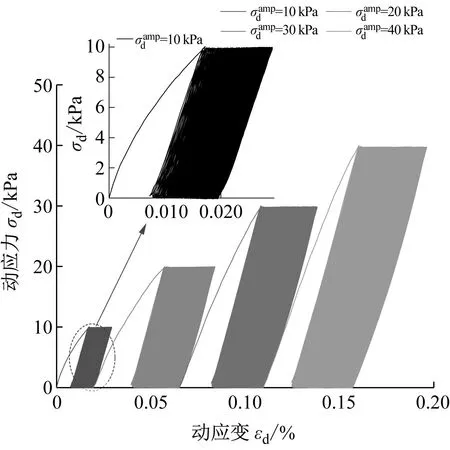
图11 不同动应力幅值下试样的滞回曲线Fig.11 Hysteresis curves of specimens with different dynamic stress amplitudes

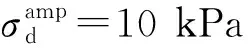
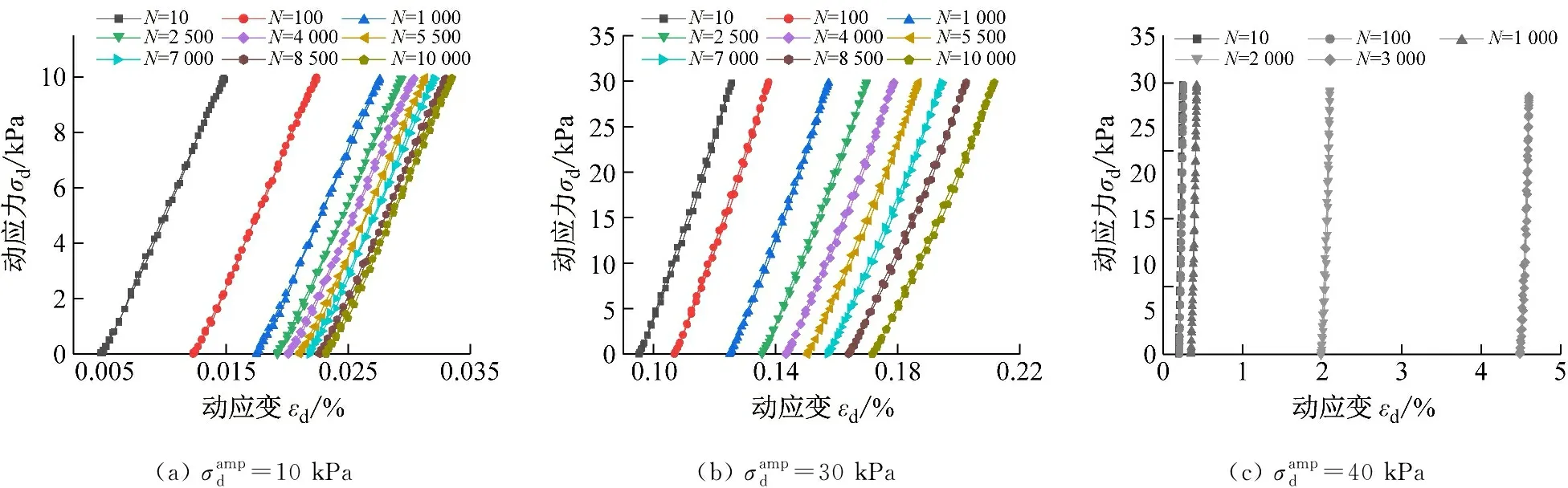
图12 滞回曲线的演化规律Fig.12 Evolution of hysteresis curve

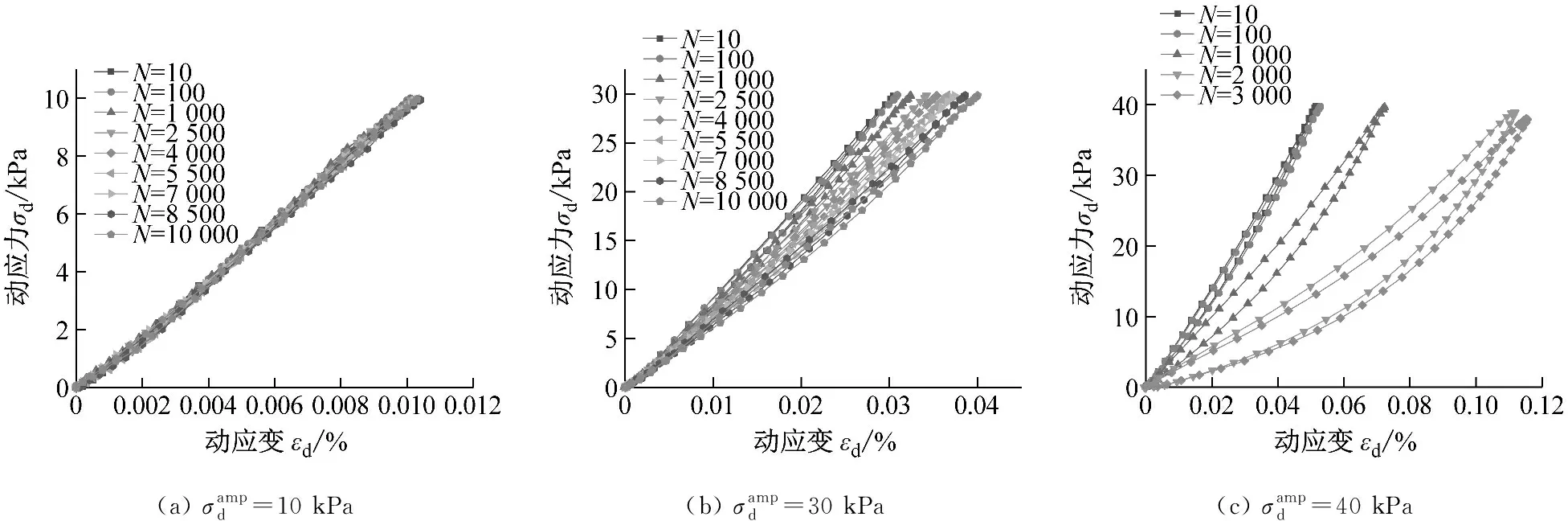
图13 横坐标变换后滞回曲线的演化规律Fig.13 Evolution of the hysteresis curve after the horizontal coordinate transformation

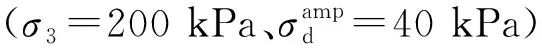
(a) 不同

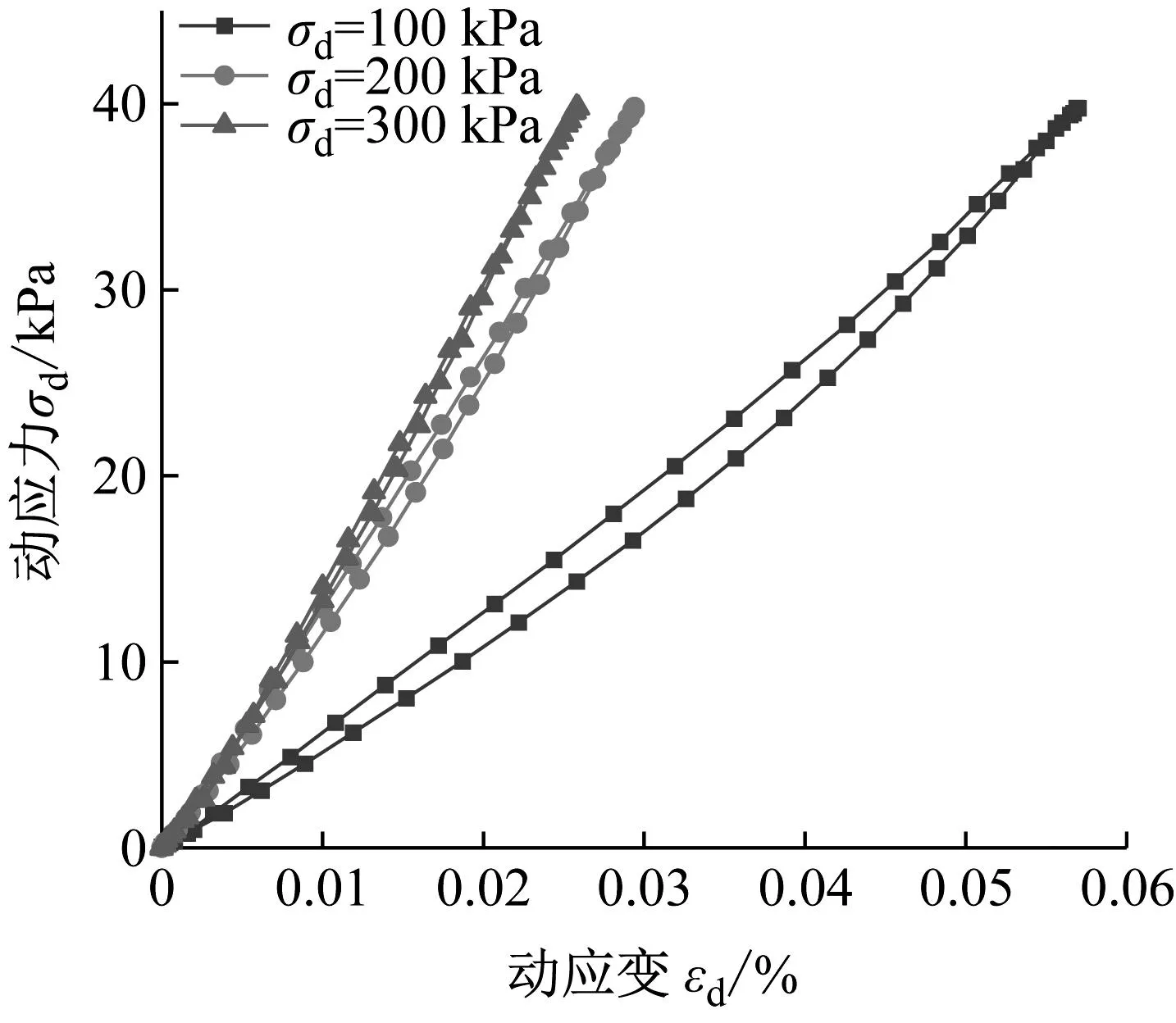
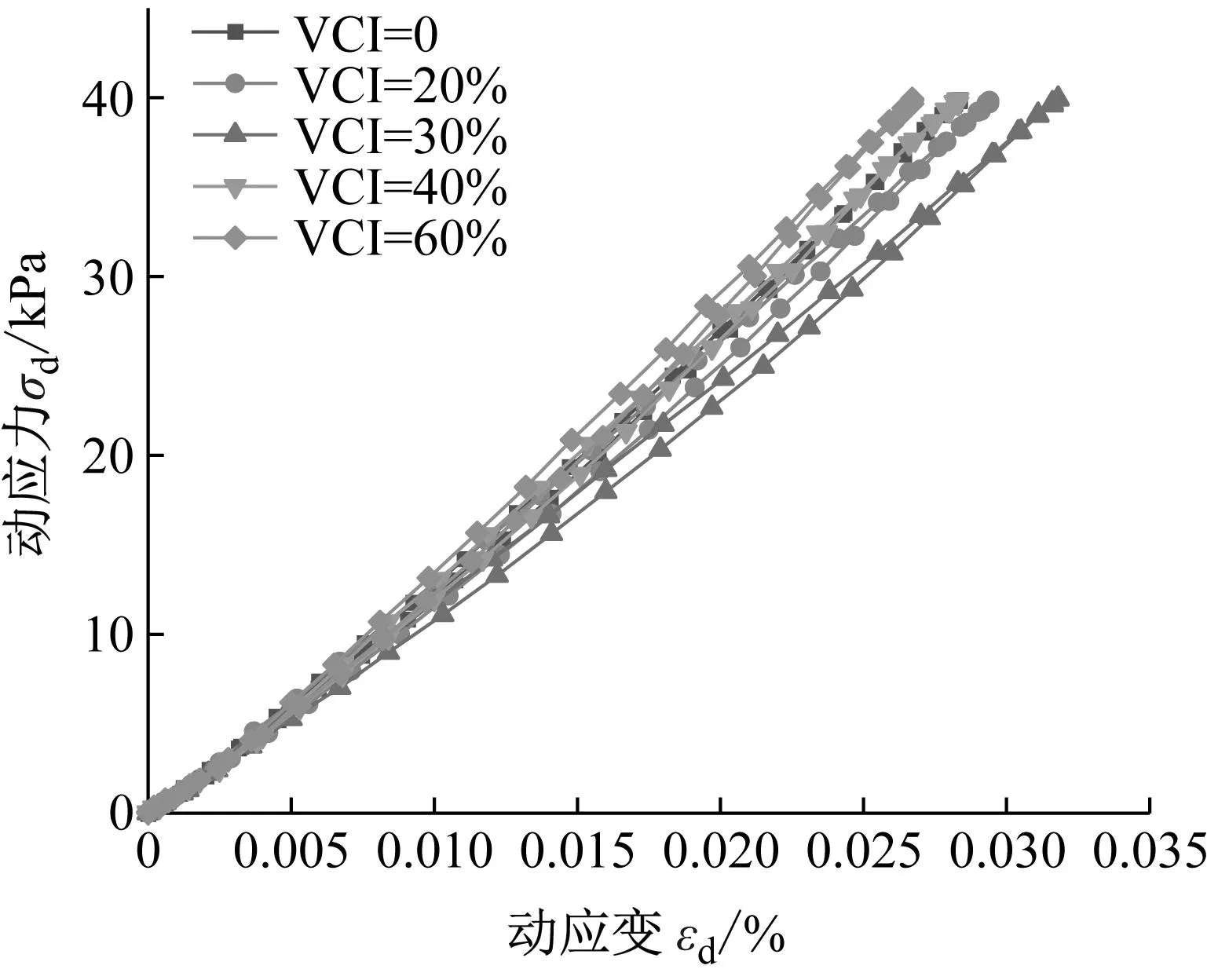
(b) 不同围压图14 不同VCI及围压下试样滞回曲线的演化规律(N=10 000)Fig.14 Evolution of hysteresis curves for specimens with different VCI and confining pressures (N=10 000)

从图14(a)中可以看出,随着VCI的增加,滞回曲线的倾斜度呈先减小后增加的趋势,试样经历了从软化到硬化的过程。滞回曲线面积的大小可以表示每次循环加载过程中试样能量损耗的多少。由图14(a)可知,滞回曲线的面积随着VCI的增加先增加后减小,当VCI小于30%时,滞回曲线面积增加,当VCI大于30%时,滞回曲线面积减小,这表明试样内部损耗的能量经历了由多到少的过程。而从图14(b)中可以看出,随着围压的增大,滞回曲线的倾斜程度逐渐增大,试样的回弹模量增大,试样经历了明显的硬化。同时,滞回曲线的面积逐渐减小,这表明试样内部耗损的能量减小。

2.4 回弹模量

回弹模量被认为是检查基层和路基刚度的有效指标[31],如图15所示。回弹模量Mr定义为[32]

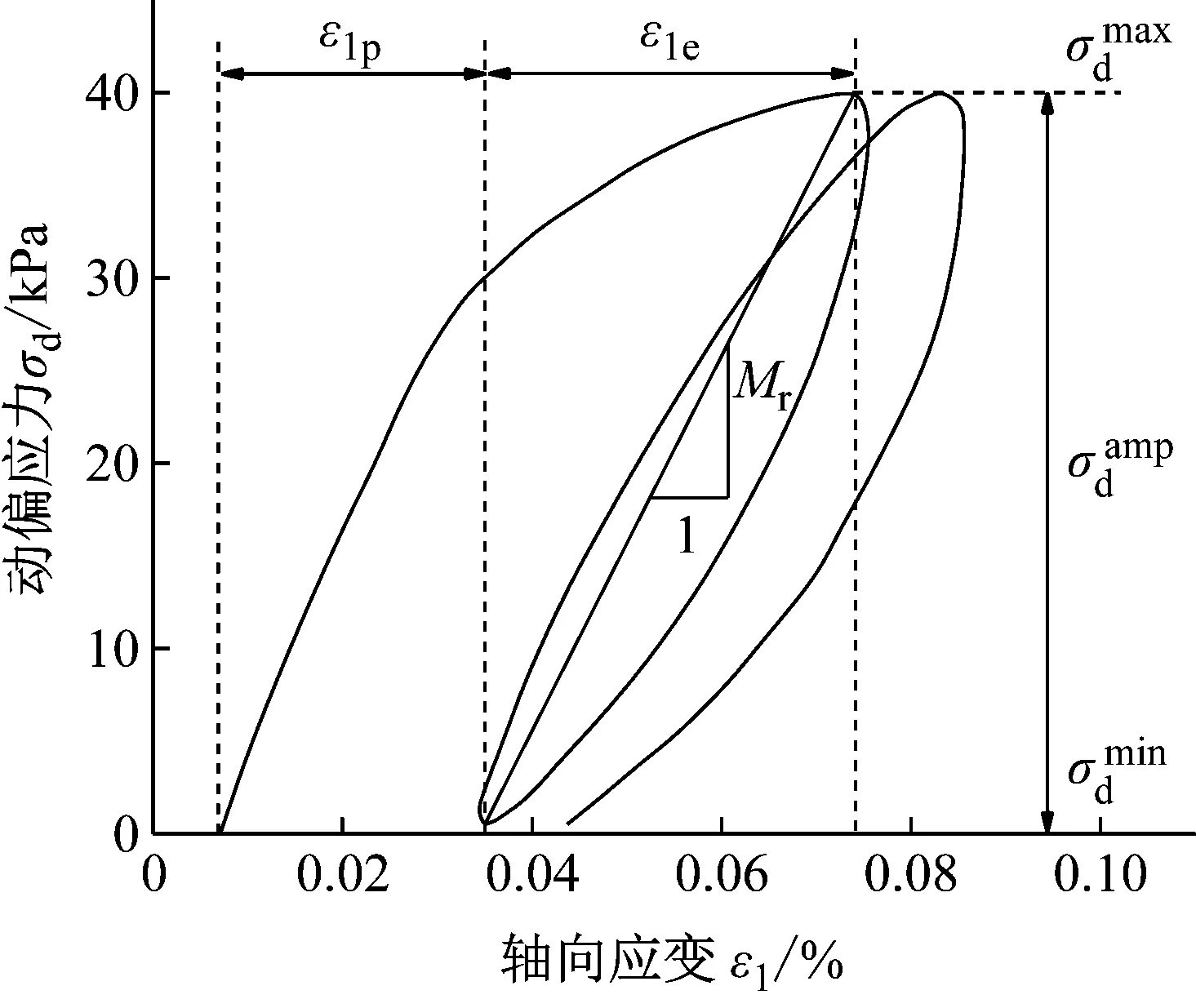
图15 回弹模量Mr的定义Fig.15 Definition of resilient modulus Mr

(3)

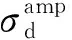
因此,对循环荷载下各个滞回曲线的回弹模量进行了提取,得到不同围压及动应力幅值条件下5种VCI指标污染圆砾的回弹模量Mr与振动次数N之间的关系曲线,如图16所示。

(a) σ3=100 kPa

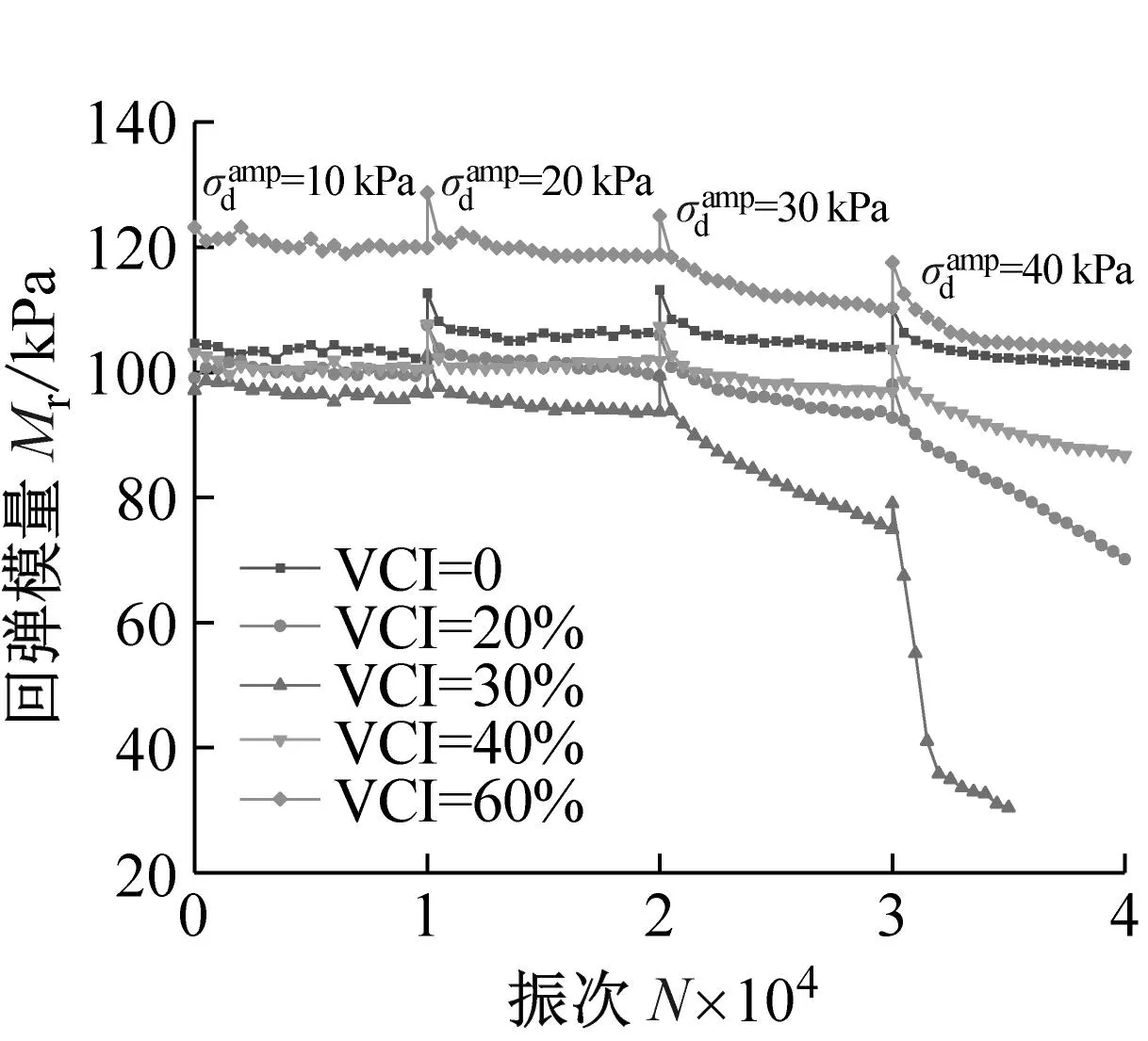
(b) σ3=200 kPa

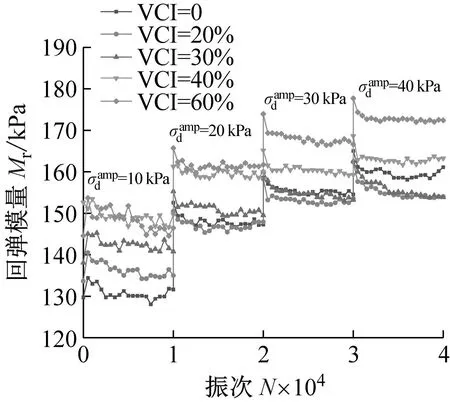
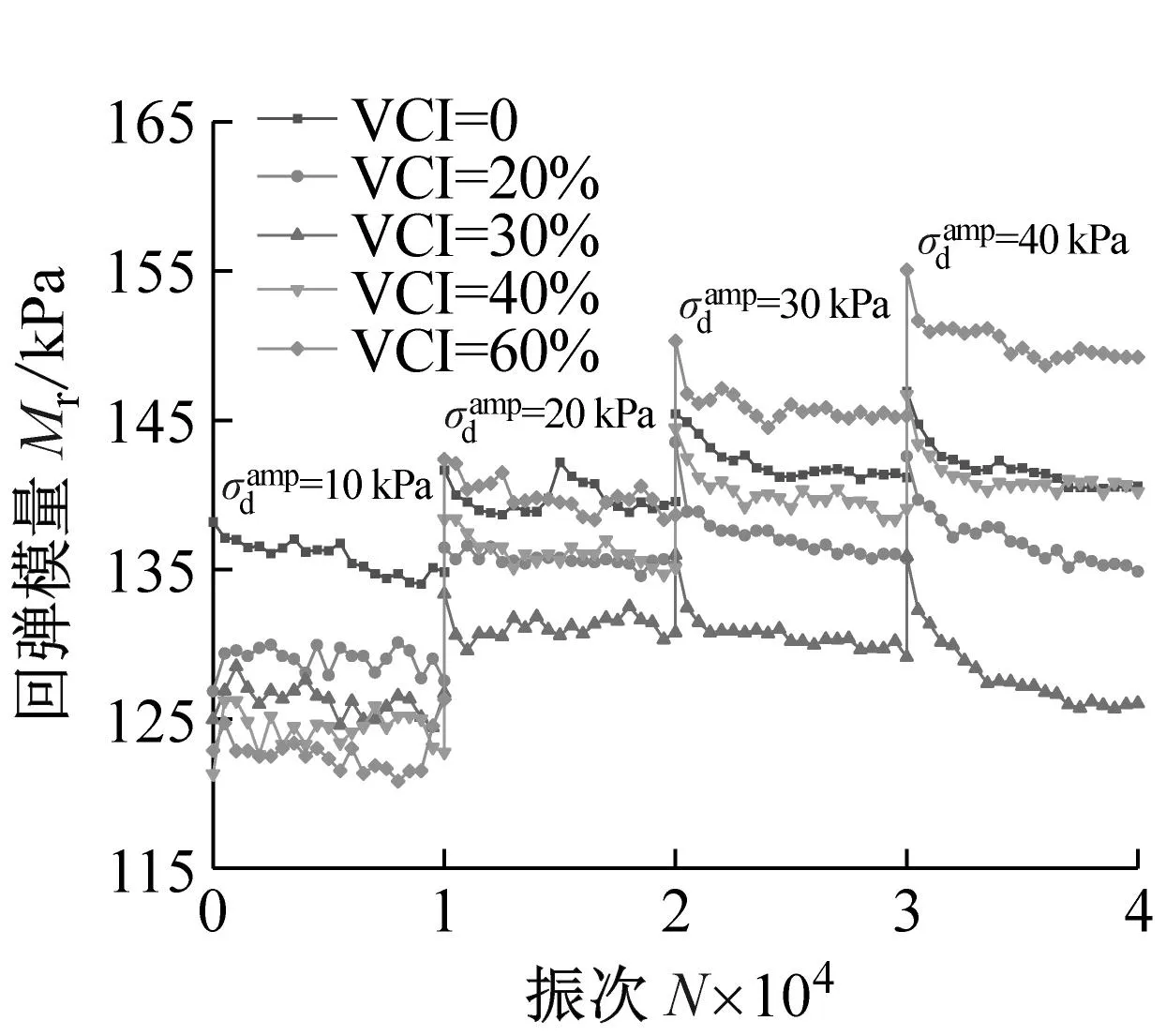
(c) σ3=300 kPa图16 污染圆砾的回弹模量Mr与加载次数N之间的关系曲线Fig.16 The relationship curve between the resilient modulus Mr of the fouled round gravel and the number of loading N

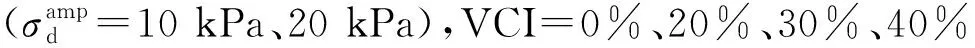
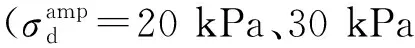
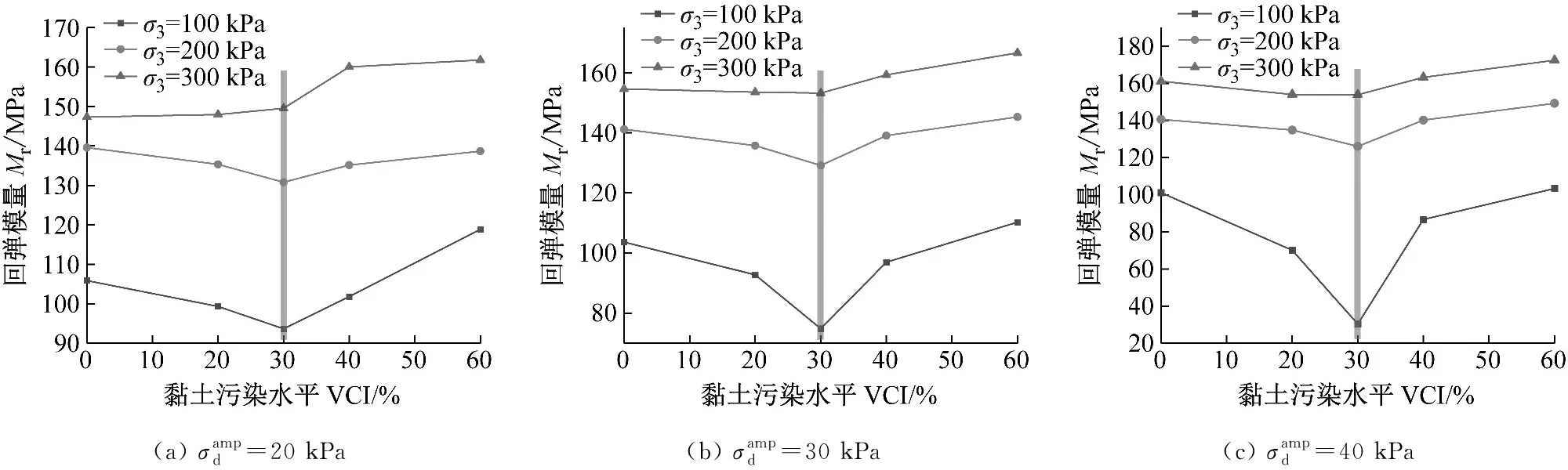
图17 各个加载阶段污染圆砾的最终回弹模量Mr与黏土污染水平VCI之间的关系曲线Fig.17 The relationship curve between the final resilient modulus Mr and the clay fouling level VCI of the fouled round gravel at each loading stage

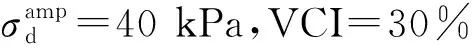
2.5 动孔压比分析

为便于对不同工况下的试验结果进行对比及理解,本文将动孔隙水压力进行归一化处理,转化为相应的动孔压比ru

(4)

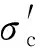
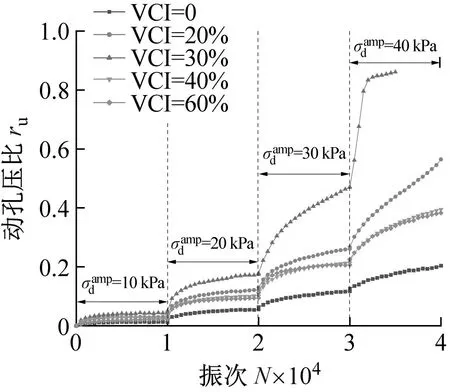
(a) σ3=100 kPa

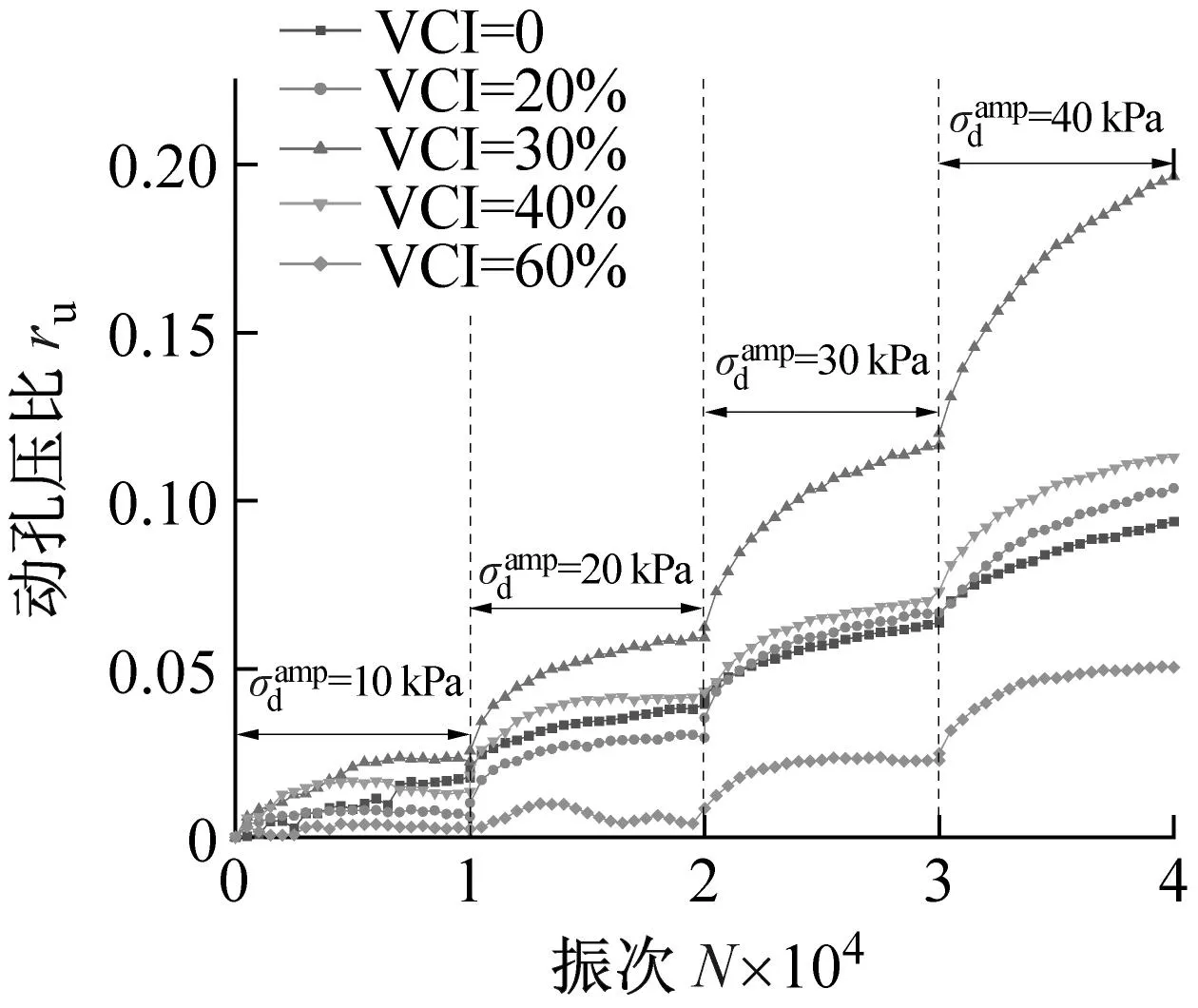
(b) σ3=200 kPa

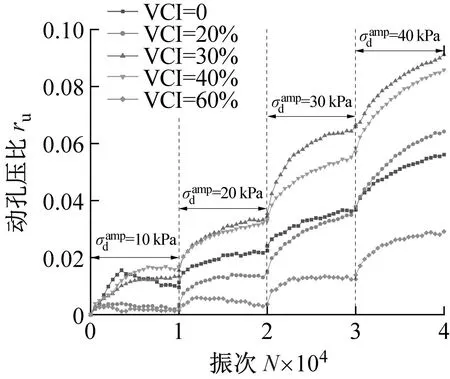
(c) σ3=300 kPa图18 污染圆砾的动孔压比ru与加载次数N之间的关系曲线Fig.18 The relationship curve between the dynamic pore pressure ratio ru of the fouled round gravel and the number of loading N

3 结 论

本文以黏土污染的圆砾为研究对象,利用GDS大型三轴循环试验系统,开展了一系列饱和不排水动三轴试验。探究了不同围压及动应力幅值下黏土污染水平对圆砾长期动力特性的影响,以揭示地铁循环荷载作用下,污染圆砾路基的长期服役性能。本研究得到如下结论:

(1) 试样的累积塑性应变随着VCI的增加呈先增后减的趋势,黏土由润滑作用逐渐转变为填充作用。同时,围压的增大会造成界限VCI在一定程度上降低,当σ3=100 kPa时,界限VCI=30%,当σ3=200 kPa、300 kPa时,界限VCI转变为20%,但总体还是介于20%-30%之间。

(2) 对于埋深较浅(σ3=100 kPa)的地铁隧道,VCI对试样的累积塑性应变影响较大,为了保证地铁的行车安全,应对圆砾土地基的强度进行提升,而对于埋深较深(σ3=200 kPa、300 kPa)的地铁隧道,VCI对试样的累积塑性影响较小,地铁运行是相对安全的。

(3) 随VCI的增加,试样的弹性应变先增大后减小,回弹模量则先减小后增大。同时,两者的变化趋势均随围压的减小及动应力幅值的增大愈发明显。

(4) 试样在弹性状态时,滞回曲线趋于密集,其倾斜度无明显变化,回弹模量恒定。在塑性状态时,滞回曲线密度减小并逐渐维持恒定,其倾斜度缓慢减小,回弹模量缓慢降低。在破坏状态时,滞回曲线间隔快速增大,倾斜度快速减小,回弹模量急剧降低。

(5) 动孔压比随着VCI的增加呈现先增加后降低的趋势。同时,围压越小,动应力幅值越大,动孔压比则越大,其最大值可达0.86左右。