基于热流固耦合的液膜密封动态追随性分析

宋 勇, 于 博, , 郝木明, 王陈寅, 李天照, 任宝杰

(1. 西安航天动力研究所, 西安 710100; 2. 中国石油大学(华东) 新能源学院, 山东 青岛 266580;3. 东营海森密封技术有限责任公司, 山东 东营 257081)

以其极少的泄漏程度及耐用性为特点,液膜密封已在各种行业如石油化工与航空航天中展现出巨大的应用潜力。在航空航天行业中,高参数运行环境下,热力变形、轴向振动以及角向偏摆等现象屡见不鲜,这些都是导致密封失稳乃至无法工作的常见原因。因此,对液膜密封在热流固耦合作用下的动态追随性展开研究显得至关重要。

实际操作中液膜密封的端面流体膜厚度常随工况参数的变化而进行动态调节。整个过程不仅受到流体膜的空化效应影响,且热弹性变形与端面间隙流体的热黏效应同样在对其产生作用,这些多个因素都极大地影响了液膜密封的动力学特性。从国内外的种种研究中可以看到,提及机械密封的热流固耦合问题,无不留下了Ma等[1-3]学者们深入研究的痕迹。他们在不同工况中分别建立了相应热流固耦合仿真模型,计算出压力场与温度场等数据,并分析出各类参数对密封性能的影响。然而,大部分的研究虽然都着眼于液膜密封摩擦副的热流固耦合模型,但多数没有采取双向耦合分析,因此对于摩擦副变形对膜厚特性的反馈和对机械密封的动态特性研究仍显不足。

此外,为了有效地控制转轴的剧烈振动并避免由于密封环安装误差以及热弹变形过大引发的密封工况失稳,许多学者在机械密封的动力学特性上投入了大量精力。Etsion等[4]建立了挠性安装环的三自由度方程,并用小扰动法将方程线性化,假设轴向和角向不互相影响且始终保持稳定,从而得出了角向稳定的条件。这为后来的机械密封动力学研究奠定了理论基础。孟祥凯等[5-7]也对此进行了研究,他们就多个自由度下密封动态特性中的刚度系数与阻尼系数等进行了详细计算。但,单依靠这些分析对液膜密封的动力学特性作出评价似乎过于片面,而需要更加具体和直观的研究。于是部分学者开始针对密封的振动性能进行研究[8],就动态追随性而言,Lee等[9]通过动态分析得到非定常可压缩雷诺方程的修正形式,在给定的密封压力下,确定了初始压力分布和初始关闭力。考虑了外部冲击扰动引起的位错,包括仅动环跳动、仅静环不对中和混合位错。陈源等[10]对不同挠性安装形式对干气密封动态追随性影响进行分析。张树强等[11]又分析了动压式、静压式及混合式三种密封的弹簧和密封圈刚度和阻尼对气膜密封动态追随性的影响规律,认为动压式气膜密封的追随性最好,静压式气膜密封的追随性最差。就目前研究而言,针对密封的动力学特性研究,尤其关于其动态追随性研究,已有建树但数量不足,且大多集中于干气密封。

综上而言,液膜密封在高参数工况下会产生热弹变形,影响液膜间隙,从而进一步影响到密封的动力学稳定性。但针对液膜密封在热流固耦合作用下的动态追随性的定量研究尚不充足。本文基于小扰动法及热动力润滑理论,建立了考虑非补偿环轴向振动、角向偏摆的补偿环三自由度运动方程,并对比并分析了纯流场及热流固耦合模型下操作工况参数、力学元件参数、结构参数对动态追随性的影响,为密封振动特性的相关研究提供理论参考。

1 物理模型

1.1 密封结构

图1所示分别为密封环端面的螺旋槽型结构和密封端面间隙示意图,端面槽型采用对数螺旋线并于动环内径处开槽,其螺旋线在极坐标下公式为r=rieθtan φ,ri和ro分别为内外半径,rg为槽径,φ为螺旋角,ω为密封环旋转角速度,内外径处压力分别为pi和po,hg为螺旋槽槽深,台区和坝区槽深为0。热流固耦合作用下,密封动静环端面之间的间隙为非平行平面,如图1(b)所示,此时动、静环的热弹变形量分别为δr和δs,hmin为液膜密封端面轴向力平衡作用下的考虑变形时的最小厚度。

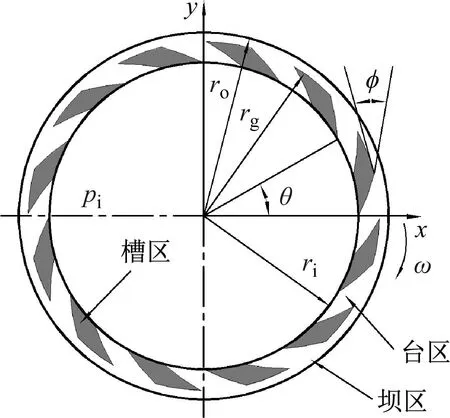
(a) 密封端面槽型结构

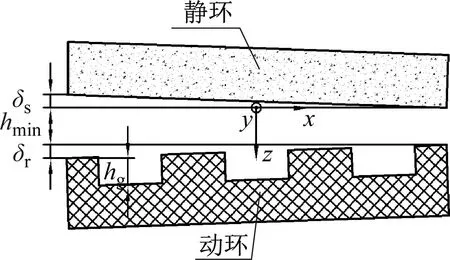
(b) 密封端面间隙图1 密封端面槽型结构及端面间隙示意图Fig.1 Schematic diagram of sealing end groove structure and end face gap

1.2 结构及操作参数

计算模型中端面槽型结构和操作参数如表1所示。螺旋槽密封动、静环的材料物性参数如表2所示。后续计算中,除被分析参数外,其余均保持不变。

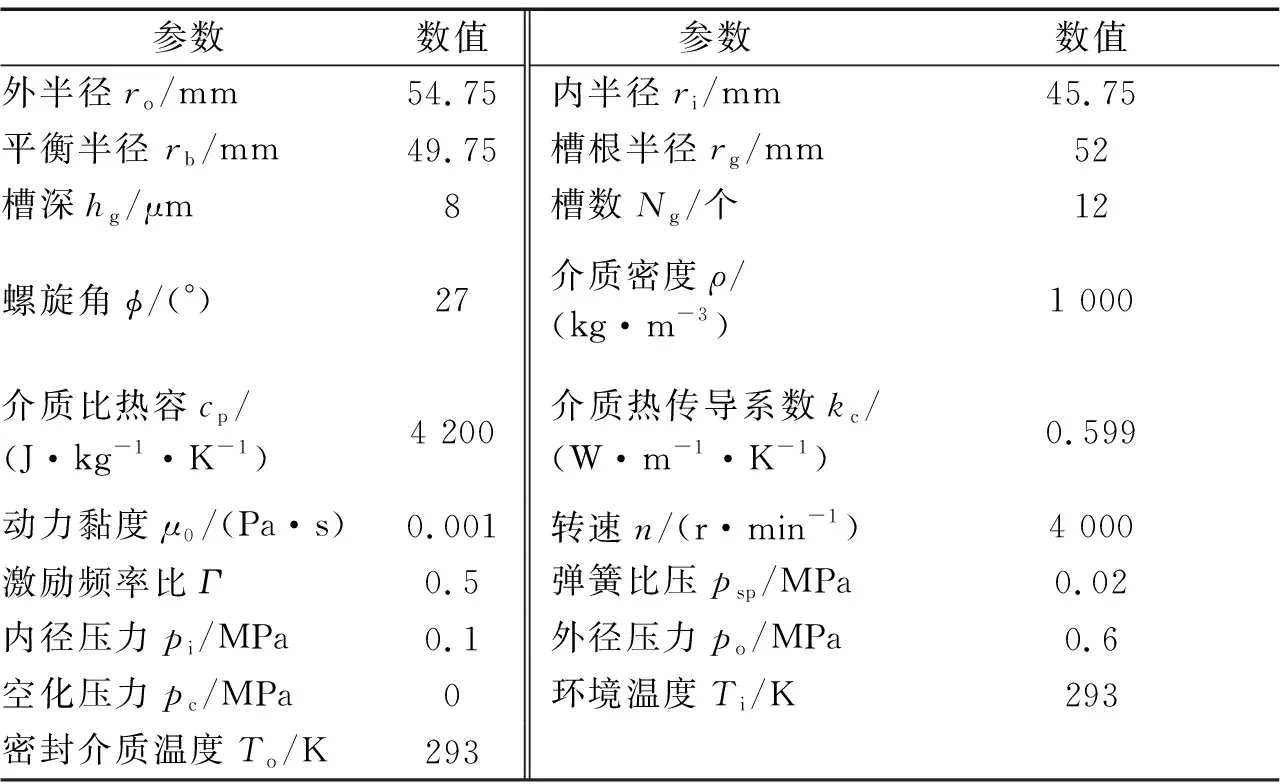
表1 端面结构参数和操作参数Tab.1 Structural and operational parameters of end face

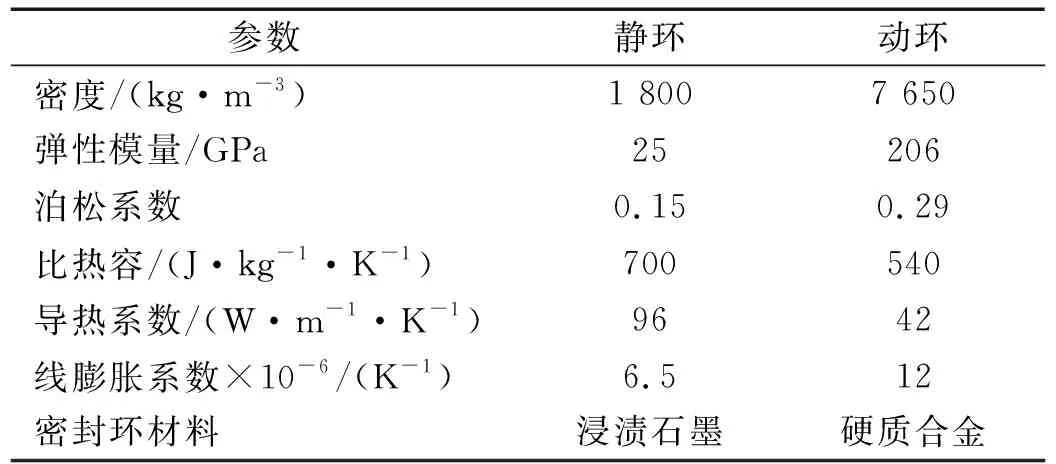
表2 密封环材料参数Tab.2 Material parameters of sealing rings

1.3 数学模型

采用有限体积法离散控制方程,配合以经典二维结构化矩形网格求解雷诺润滑方程和能量方程。而下文,具体介绍了计算所需各控制方程及边界条件。

此外,同时调用商业有限元软件ANSYS APDL求解热-流-固耦合过程中密封环的轴向截面温度和变形。

首先,利用MATLAB软件求解端面压力和热流密度后,参数传递至ANSYS APDL,以利用ANSYS APDL参数化设计语言求解端面温度和变形。最后又将该参数返回MATLAB以更新膜厚并重新迭代,直至收敛。以此,实现多物理场双向耦合的问题。

1.3.1 雷诺方程

考虑空化效应,计入JFO空化边界,可得的极坐标系下的液膜瞬态雷诺方程如下[12]

(1)

式中:Φ为液膜密度比;Φ=ρ/ρL,ρ为密度,ρL为液体密度。

1.3.2 考虑空化的微扰雷诺方程

考虑密封环的轴向振动和角向偏摆,如图2所示。液膜膜厚在扰动频率υ下平衡位置具有独立的三自由度的微扰位移。

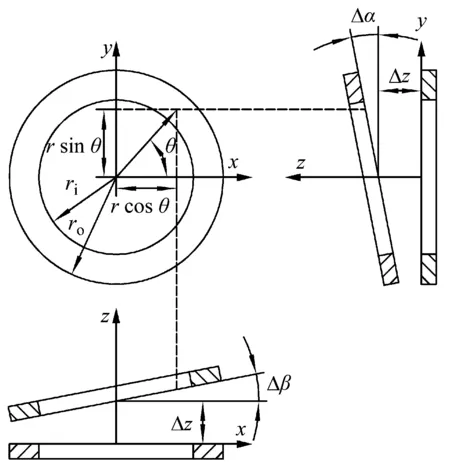
图2 密封端面运动学模型Fig.2 Kinematics model of sealing face

利用小扰动法,建立考虑空化效应的稳态雷诺方程和三自由度上的微扰雷诺方程组如下

(2)

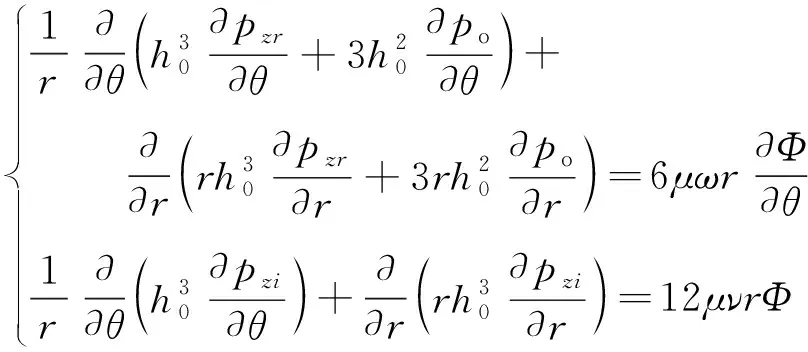
(3)

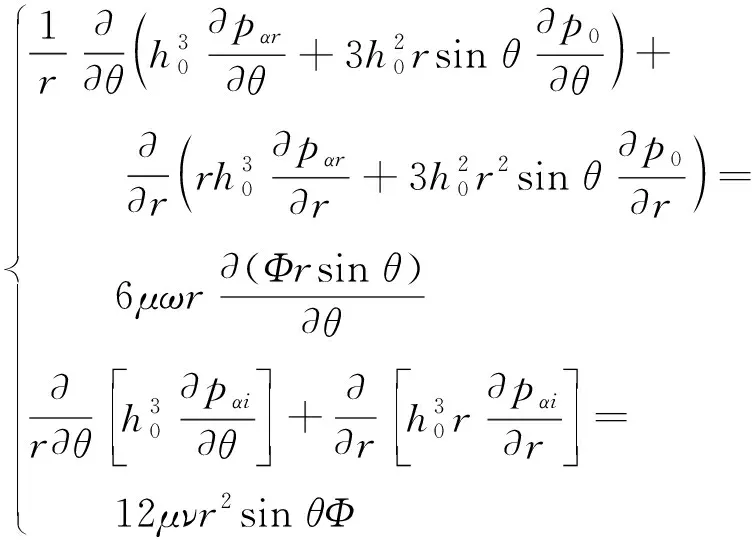
(4)

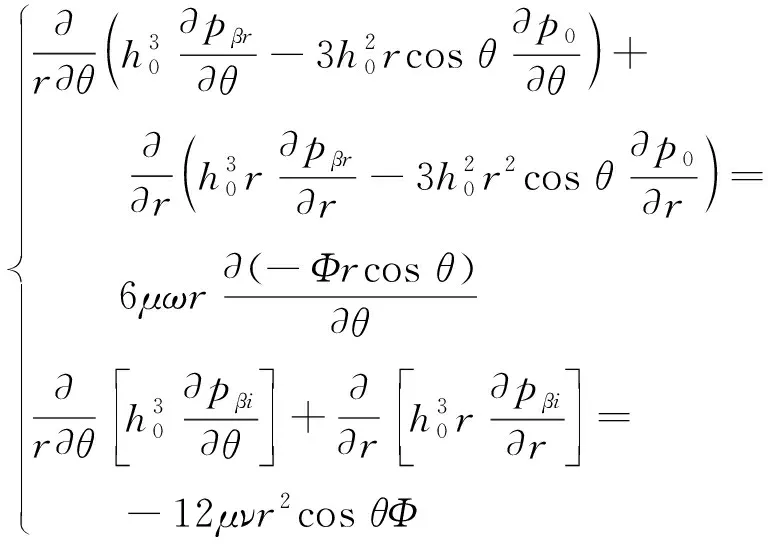
(5)

1.3.3 能量方程

根据能量守恒原理,考虑界面的热传导能量损失、流动功耗和摩擦功耗,忽略液膜轴向的热传导,可以建立极坐标下的液膜润滑能量方程为[13]

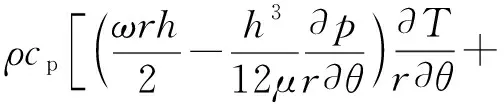
(6)

式中:ρ为介质密度;cp为介质比热容;Tr和Ts分别为动、静环端面处温度;T为流体膜温度分布;hfr和hfs分别为动、静环界面处的换热系数。

考虑到密封环发生的热弹变形和液膜的厚度在密封环轴向力平衡条件下的同时变化,密封环与液膜热流固耦合作用下,可得端面任意一点处膜厚的控制方程如下

h0(r,θ)=hmin+hg(r,θ)+hdeform(r)

(7)

式中:hmin为热流固耦合作用后平衡时的最小膜厚;hdeform为密封环变形引起膜厚的变化量,变形为考虑轴向变形。

1.3.4 边界条件

(1) 内外径处边界条件

方程的内外径边界条件设置如下

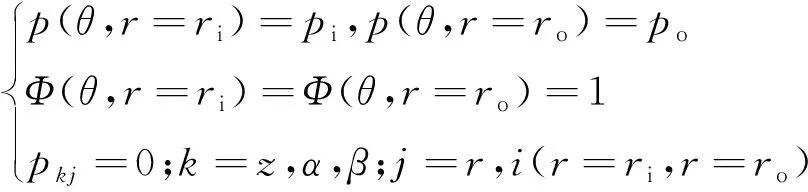
(8)

(2) 周期性边界条件

稳态雷诺方程的求解采用单周期边界,而基于此,随后的微扰雷诺方程的求解,则在密封环整个端面的全周期下进行计算。

方程的周期性边界条件设置如下

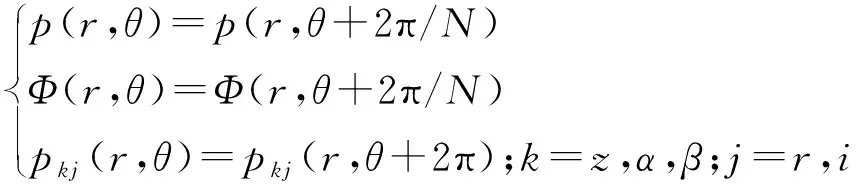
(9)

(3) JFO空化边界条件[14-15]

(10)

式中,pc为空化压力。

(4) 温度边界条件

能量方程动态温度边界条件如下

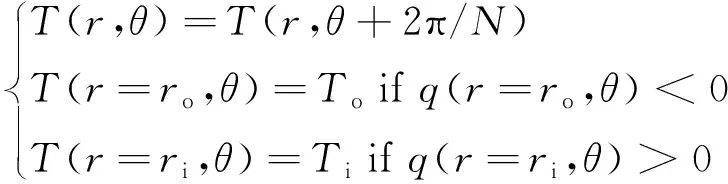
(11)

其中,

(12)

式中,q(r=ro,θ) <0和q(r=ri,θ) >0表示介质从外界流入边界处的润滑区域。

(5) 密封环的热力载荷边界条件

密封环的热弹性变形调用软件ANSYS APDL加载边界条件计算温度和变形。图3所示模型首先设置为轴对称边界,其热边界条件分别为密封环外径处的对流边界S2、S3和S11,以及液膜与密封端面之间的热流密度边界S1,其余的边界是绝热边界。力载荷边界条件包括液膜承载压力边界S1,密封环外径处的高压载荷边界S2、S3、S11。密封环内径处的低压载荷边界S6、S12,静环的背面是由弹簧作用的弹性载荷边界S4,动环背面的S8、S9、S10为固定约束边界,S7为动环径向位移约束边界,由O形环在静环上的变形引起的接触载荷边界为S5。其中,边界S1上的热通量为流经单位面积的热量,承载平均压力为开启力与密封面面积的比值。

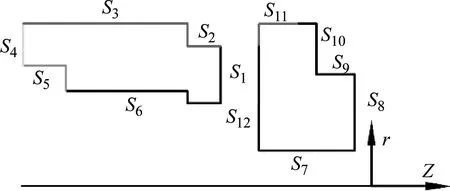
图3 密封环力热边界条件Fig.3 Thermal-elastic boundary conditions of sealing rings

1.3.5 动态追随性分析

动态追随性指,在外部干扰下保持稳定膜厚,以维持良好密封性能的能力。通过衡量液膜厚度在外界激励条件下的扰动情况,我们可以评估液膜密封动态追随性。

如图4所示,液膜密封的动力学分析模型,显示了动环和转轴,在三自由度轴向和角向的外界激励干扰下所受影响。液膜力的变化,会影响静环轴向力和角向力矩的平衡,从而改变静环对外界激励的响应运动。此时,动环和转轴的三自由度激励运动,与静环响应运动之间的位移差值,即反映出液膜密封膜厚的扰动。

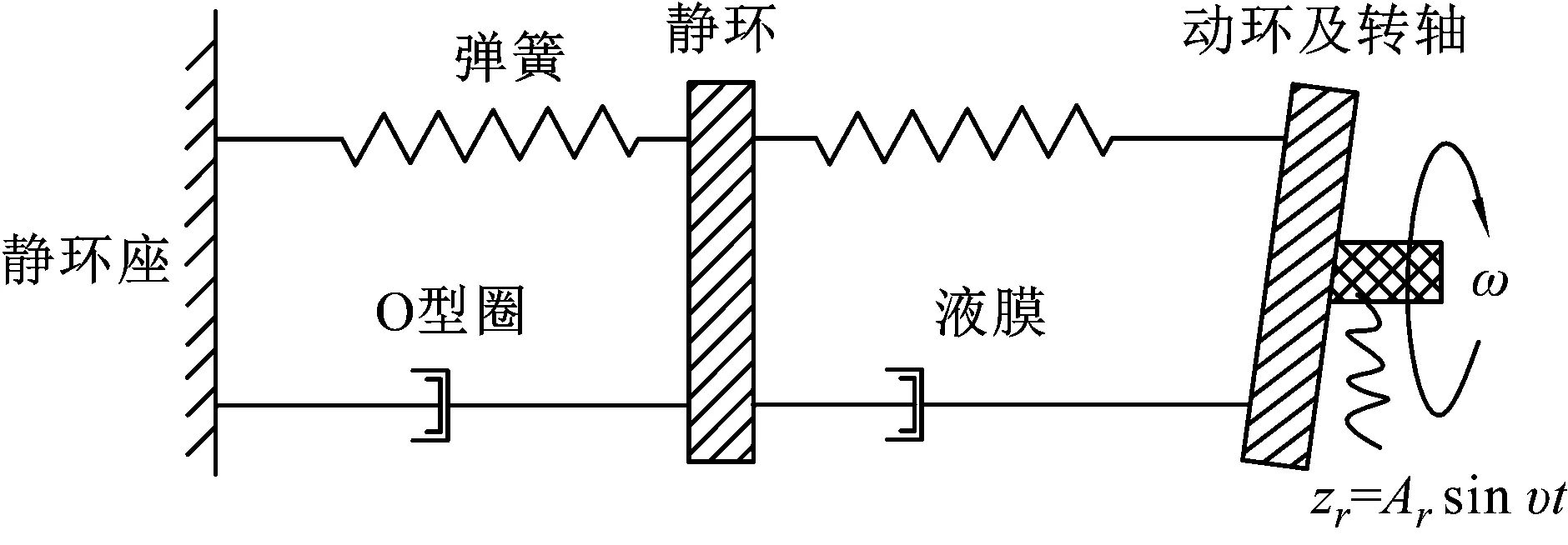
图4 液膜密封动力学分析模型Fig.4 Dynamic analysis model of liquid film seal

将液膜视为具有刚度和阻尼特性的弹簧-阻尼系统,其中静环的轴向和角向运动是解耦的,液膜密封的静环轴向和角向上的运动方程为

(13)

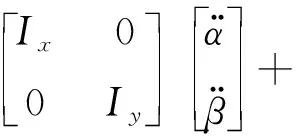
(14)

式中:z、α和β为静环的轴向和角向的响应运动;zr、αr、βr为动环的轴向和角向的激励运动;m为静环的质量,由前文所述之材料参数和尺寸计算得到;Ix、Iy为静环的转动惯量;ks为弹簧刚度;cs为O型圈阻尼;ksx、ksy为弹簧的角向刚度;csx、csy为O型圈的角向阻尼。

对于式(13)和(14),利用MATLAB调用ode45功能函数来求解二阶常系数微分方程,得静环的三自由度响应运动随时间的变化关系,进而得膜厚扰动量随时间的变化关系,其中,两个角向方程式相互耦合求解。

对于计算选取的参数基于表2和表1,增加计算参数如下:静环的质量m通过表1尺寸和密度计算得到,m= 0.2 kg;静环的转动惯量Ix=Iy=I= 5.4 × 10-4kg·m2;弹簧刚度ks= 1×104N/m;O型圈阻尼cs= 1×103N·s/m;轴向激励振幅Arz= 50 μm;角向激励振幅Ar= 500 μrad。

在下文分析中,除特殊说明参数的取值外,其他参数均按照上述取值计算。

2 结果及分析

2.1 模型验证

(1) 密封热流体润滑温度验证

本文的计算模型中,虽然将流体膜的轴向热传导忽略,仅关注动环和静环外表面的对流换热,但图5所示的计算结果大致与 Tournerie等[16]的研究一致,为热流体润滑模型的精确性提供了有力支持。然而,图5(b) 中观察到整体上的轻微差异,这可能归因于,相较于参考文献,本模型中忽略的轴向热传导,此因素对模型当前条件下的精确性产生了一定影响。

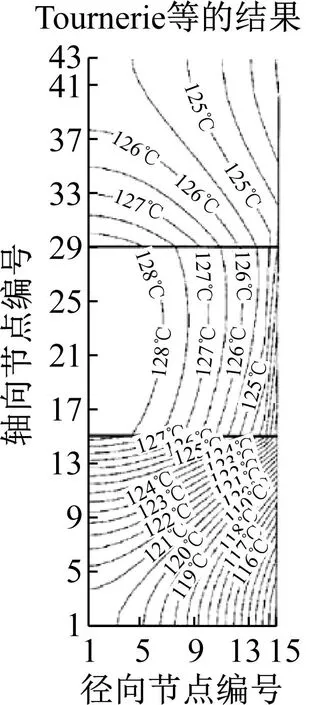
(a) 密封环轴向截面温度分布

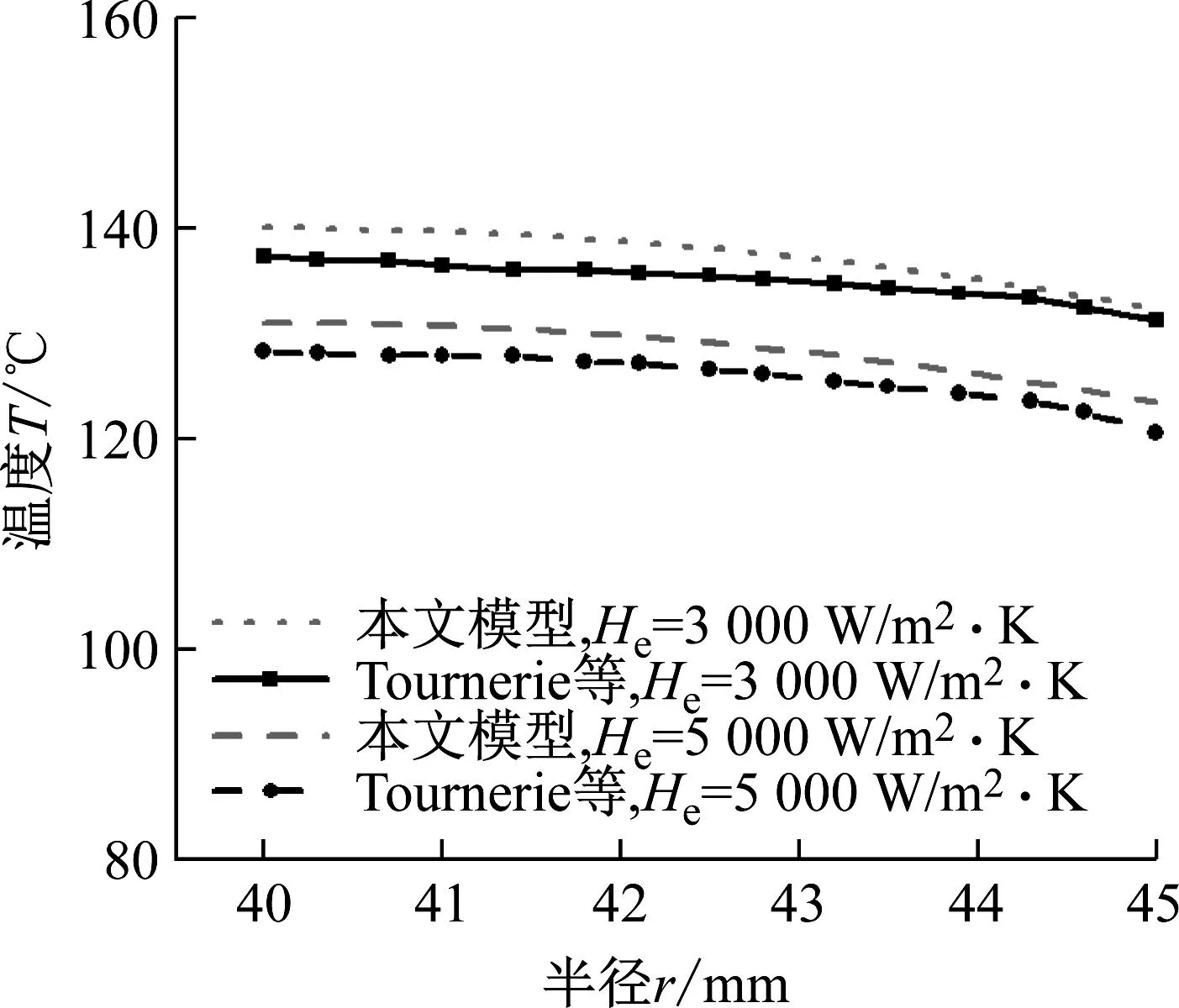
(b) 动环端面径向温度分布图5 密封热流体润滑温度文献验证Fig.5 Temperature literature verification of thermal fluid lubricated seals

(2) 密封动态特性求解验证

为了验证动态追随性程序计算的准确性,本文选取文献[11]所分析的考虑离心惯性项的螺旋槽液膜密封动态特性的参数进行计算和对比,图6所示为计算的不包含离心惯性项和空化效应的不同膜厚下的无量纲三自由度液膜动态刚度系数与文献的计算结果对比图,可以看出本文程序的计算结果与文献的计算结果基本一致,从而证明了本文计算的准确性。

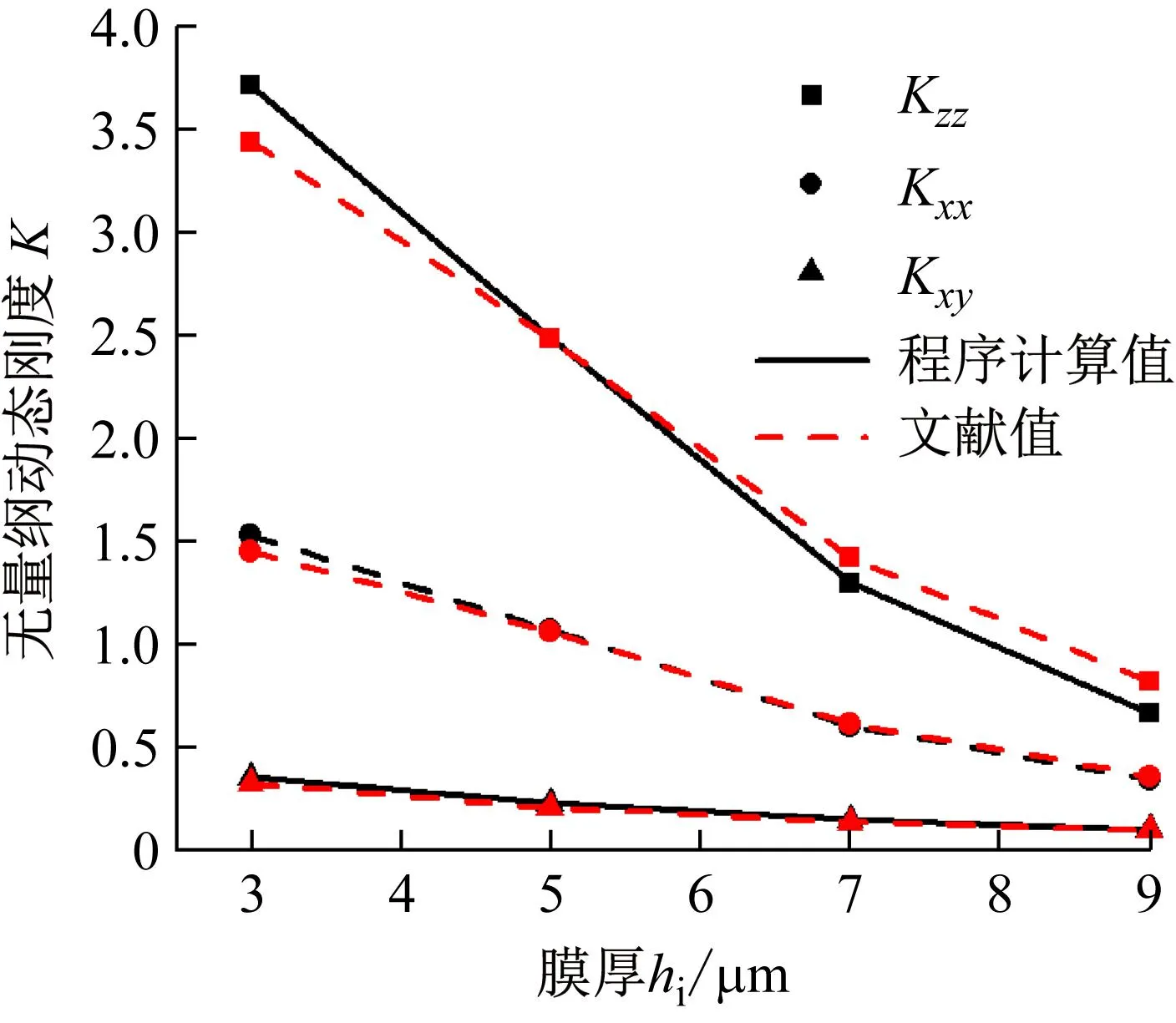
图6 液膜动态特性文献验证Fig.6 Literature verification of dynamic characteristics of liquid film

2.2 膜厚三自由度扰动运动分析

给定三角函数变化形式的外界激励作用,三自由度扰动变化如图7所示。据此,可计算得到整个端面的液膜扰动瞬态分布,并由此得最大膜厚扰动量时变曲线如图8所示,并以此反映液膜密封动态追随性。

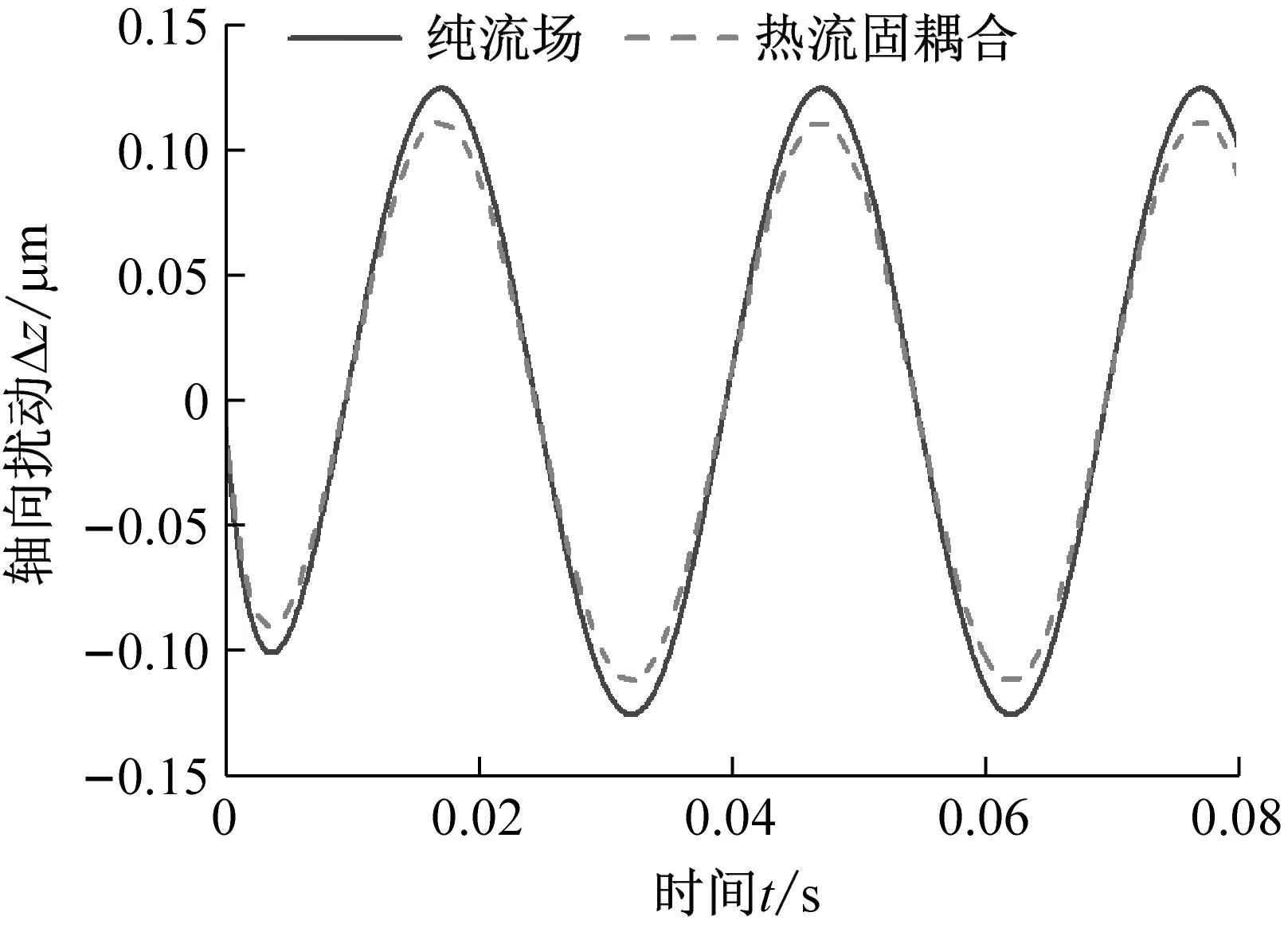
(a) 轴向扰动

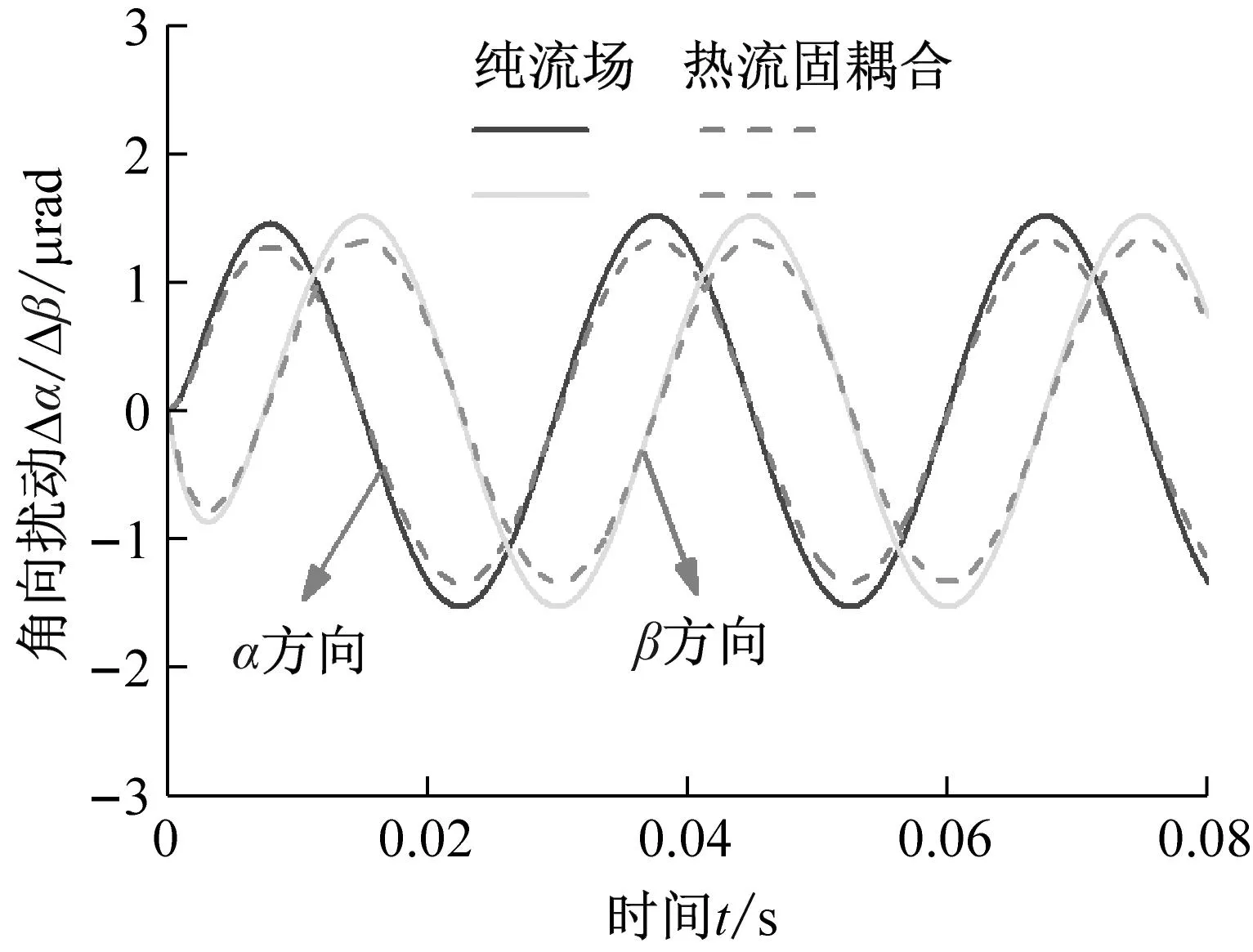
(b) 角向扰动图7 轴向和角向扰动时变曲线Fig.7 Time-varying curves of axial and angular disturbances

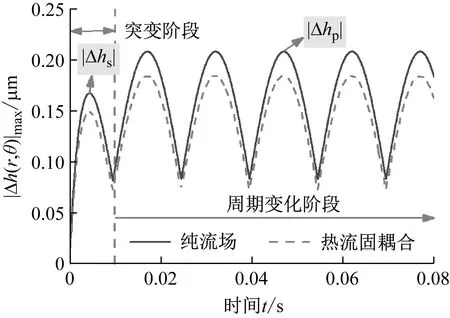
图8 膜厚最大扰动量时变曲线Fig.8 Time-varying curves of maximum perturbation of film thickness

在图8 中,膜厚最大扰动量时变曲线可分为突变阶段和周期性变化阶段。突变阶段由外界激励引发的突变扰动量组成,而周期性变化阶段来自外界激励持续作用下的膜厚稳定周期性变化量。

对比纯流场模型与热流固耦合模型下的扰动分布,发现,热弹变形与黏温效应在热流固耦合模型下,一定程度上减弱了外界激励在各自由度(轴向、角向等)各阶段(突变阶段、稳定运行阶段)上的扰动影响,与纯流场模型相比表现出一定差异。

2.3 激励振幅对动态追随性的影响

(1) 轴向激励振幅对密封动态追随性的影响

如图9所示,当Arz=0(仅有角向激励)时,角向激励提供了一个在时间上相对较为均匀的扰动响应。这是由于密封环呈现对称的环形端面结构,使得最大膜厚扰动量,在端面上360°周期旋转。轴向扰动与膜厚变化方向平行,故其响应具有继承性,响应呈现类似轴向激励的周期波动,从而,保持角向激励不变,增大轴向激励振幅,扰动呈现类似激励的,周期波动增大,不利于密封的动态追随性。此外热流固耦合模型下的动态追随性优于纯流场模型下的动态追随性。

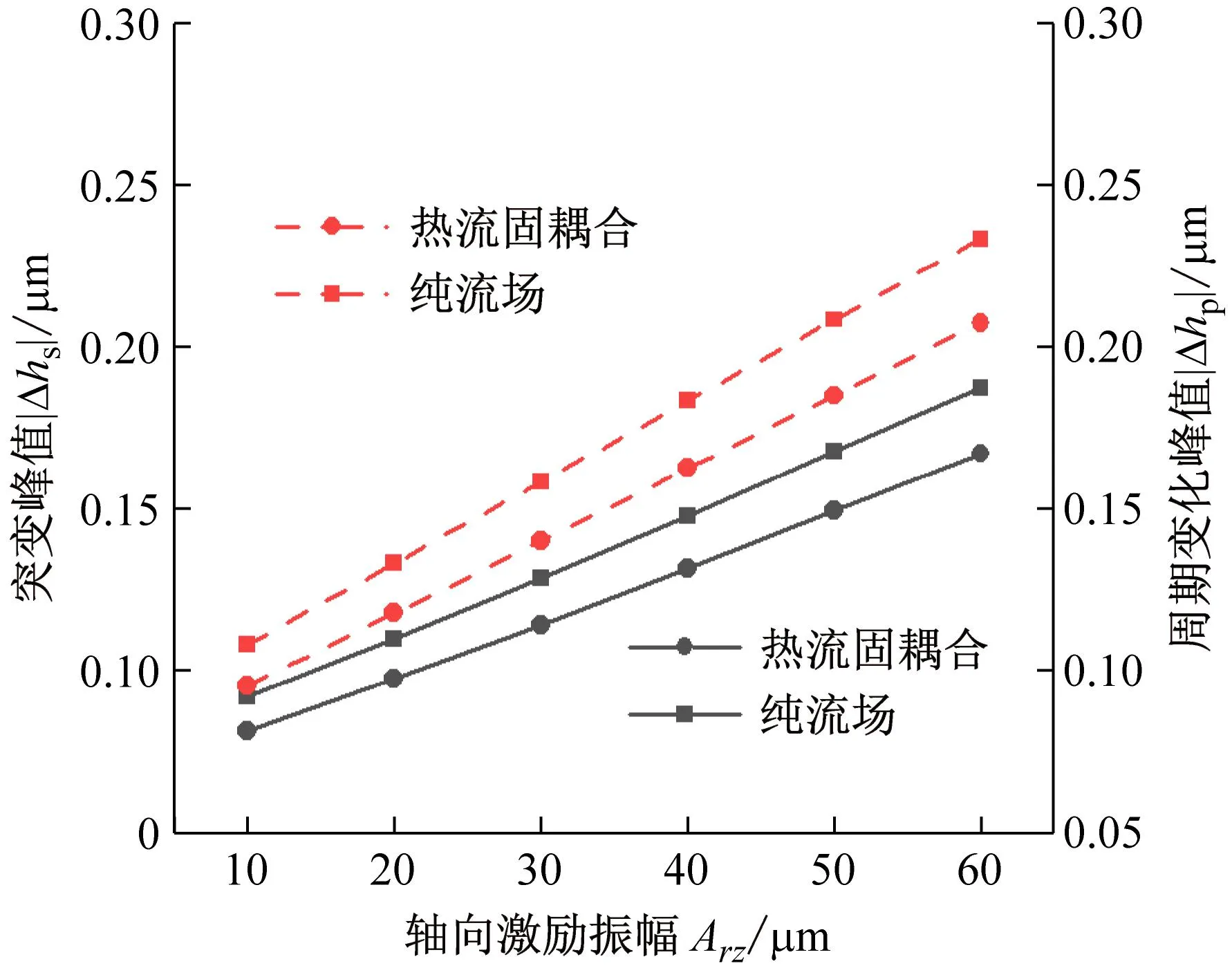
(b) 扰动峰值图9 轴向激励振幅对密封动态追随性的影响Fig.9 Effect of axial excitation amplitude on dynamic following performance of seal

(2) 角向激励振幅对密封动态追随性的影响

图10扰动分布正符合前文所述。保持轴向激励不变,不同角向激励振幅下,由于轴向激励响应具有继承性,各最大膜厚扰动量保持基本的相似性。增大角向激励振幅使得最大膜厚扰动量,整体上迁移增大,不利于密封的动态追随性。此外热流固耦合模型下的动态追随性优于纯流场模型下的动态追随性,符合前文论述。

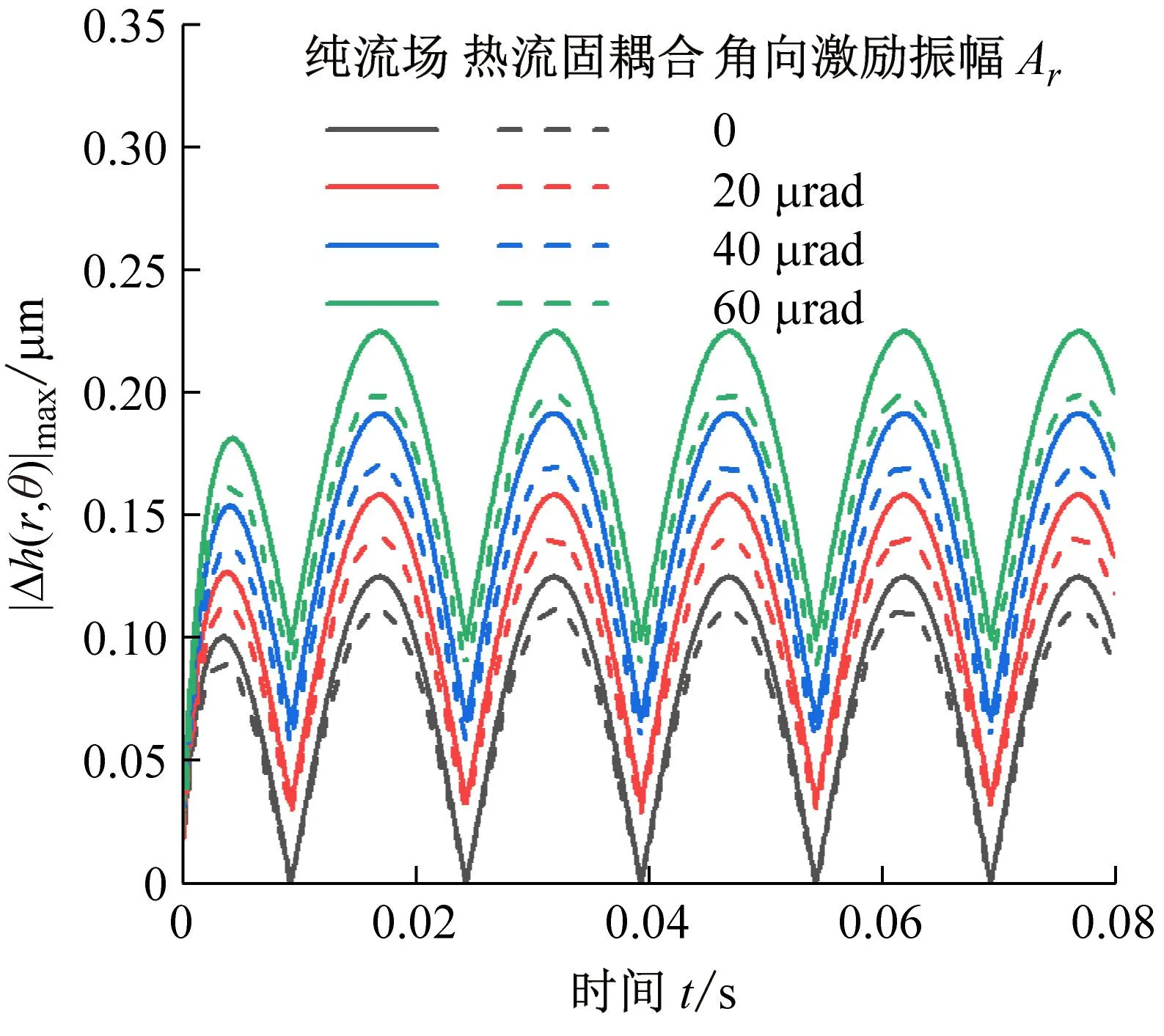
(a) 最大膜厚扰动量

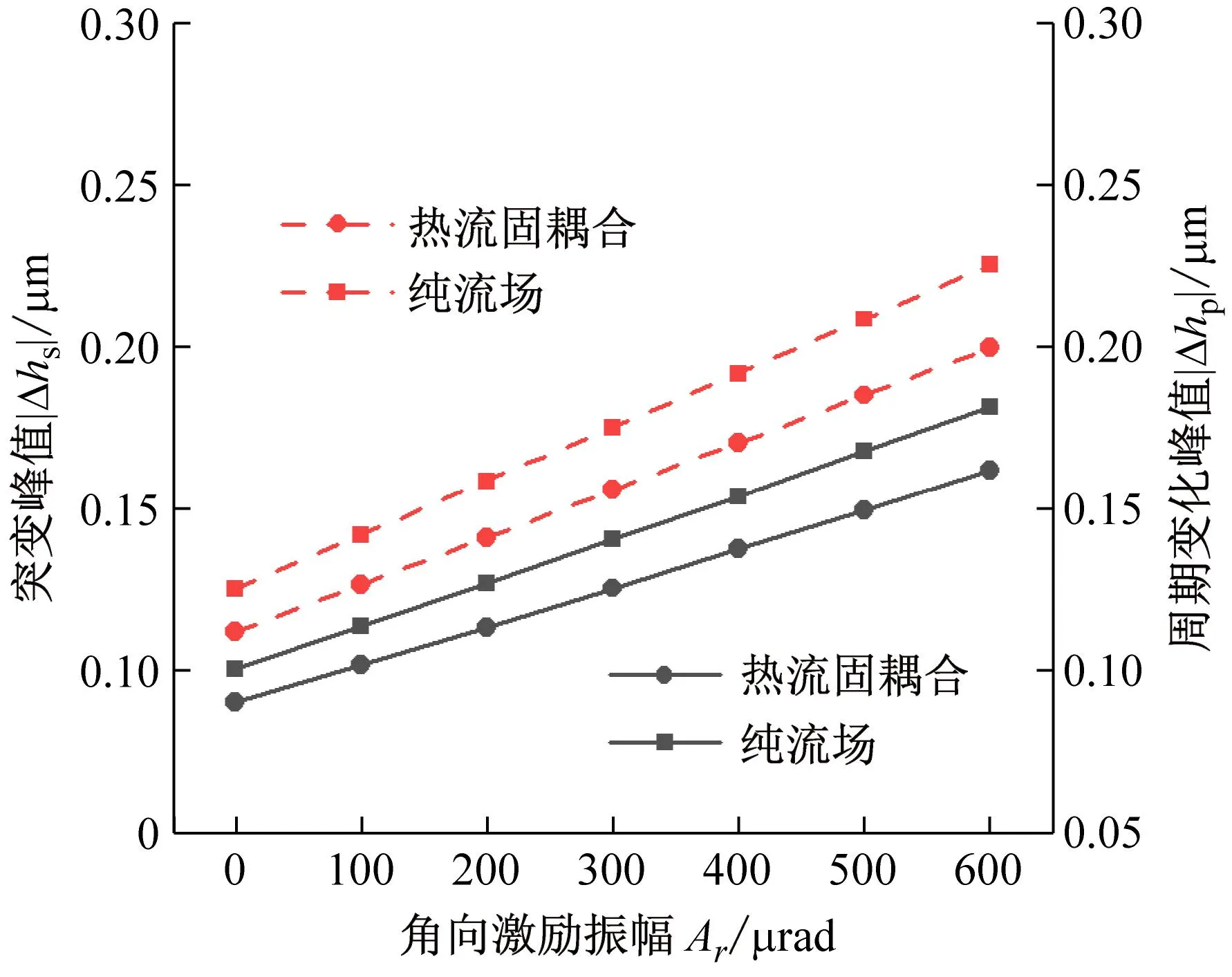
(b) 扰动峰值图10 角向激励振幅对密封动态追随性的影响Fig.10 Effect of angular excitation amplitude on dynamic following performance of seal

2.4 力学元件参数对动态追随性的影响

(1) 弹簧刚度对密封动态追随性的影响

如图11所示,弹簧刚度增加,一方面提高了响应延迟,使得扰动响应整体上发生相位右移,另一方面削弱了补偿空间,补偿环补偿能力下降,扰动响应增大。极限条件下弹簧刚度无穷,补偿环补偿能力为零。因此,可选用小刚度的弹簧来提升液膜密封的动态追随性。此外热流固耦合模型下的动态追随性优于纯流场模型下的动态追随性,符合前文论述。

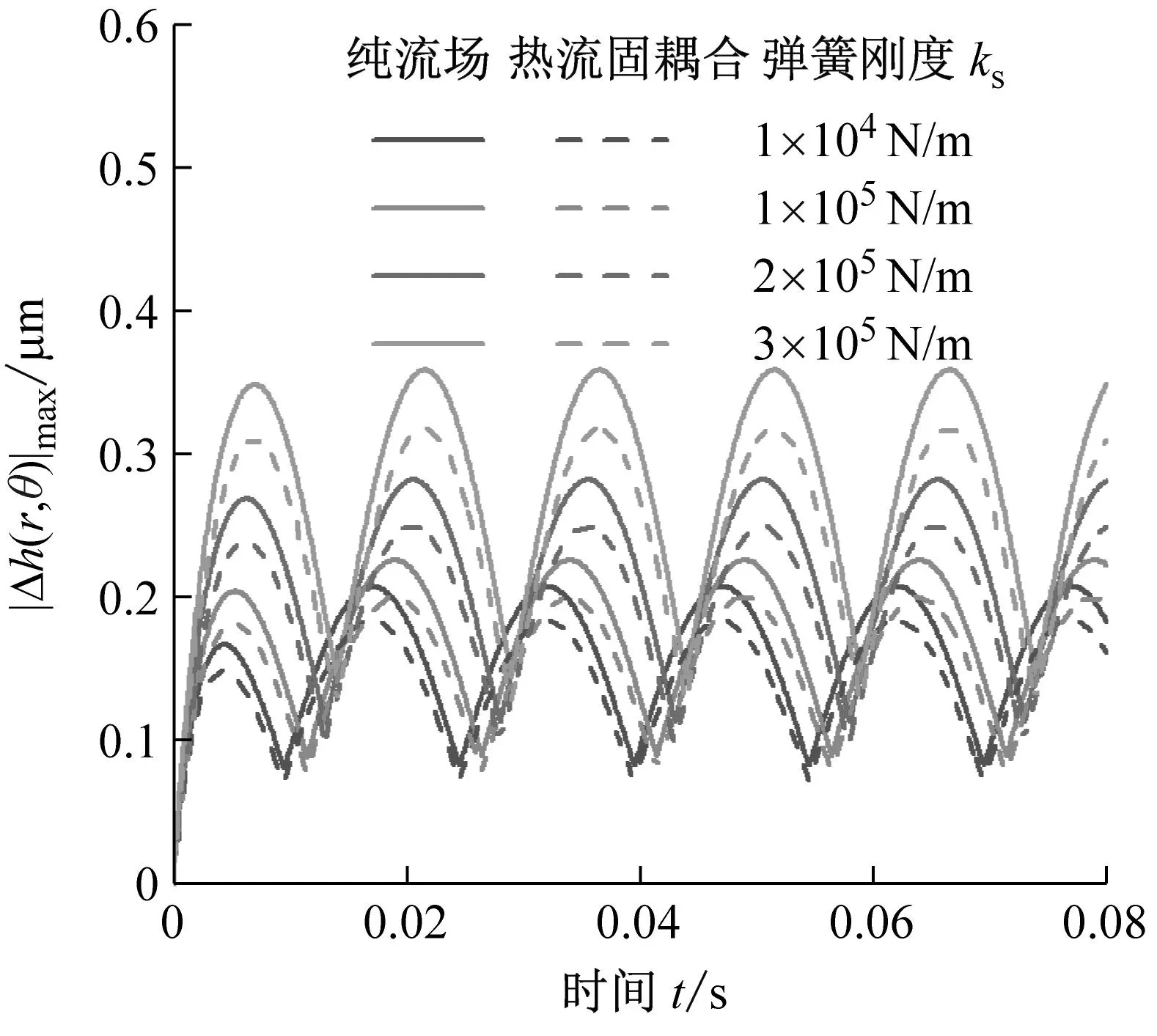
(a) 最大膜厚扰动量

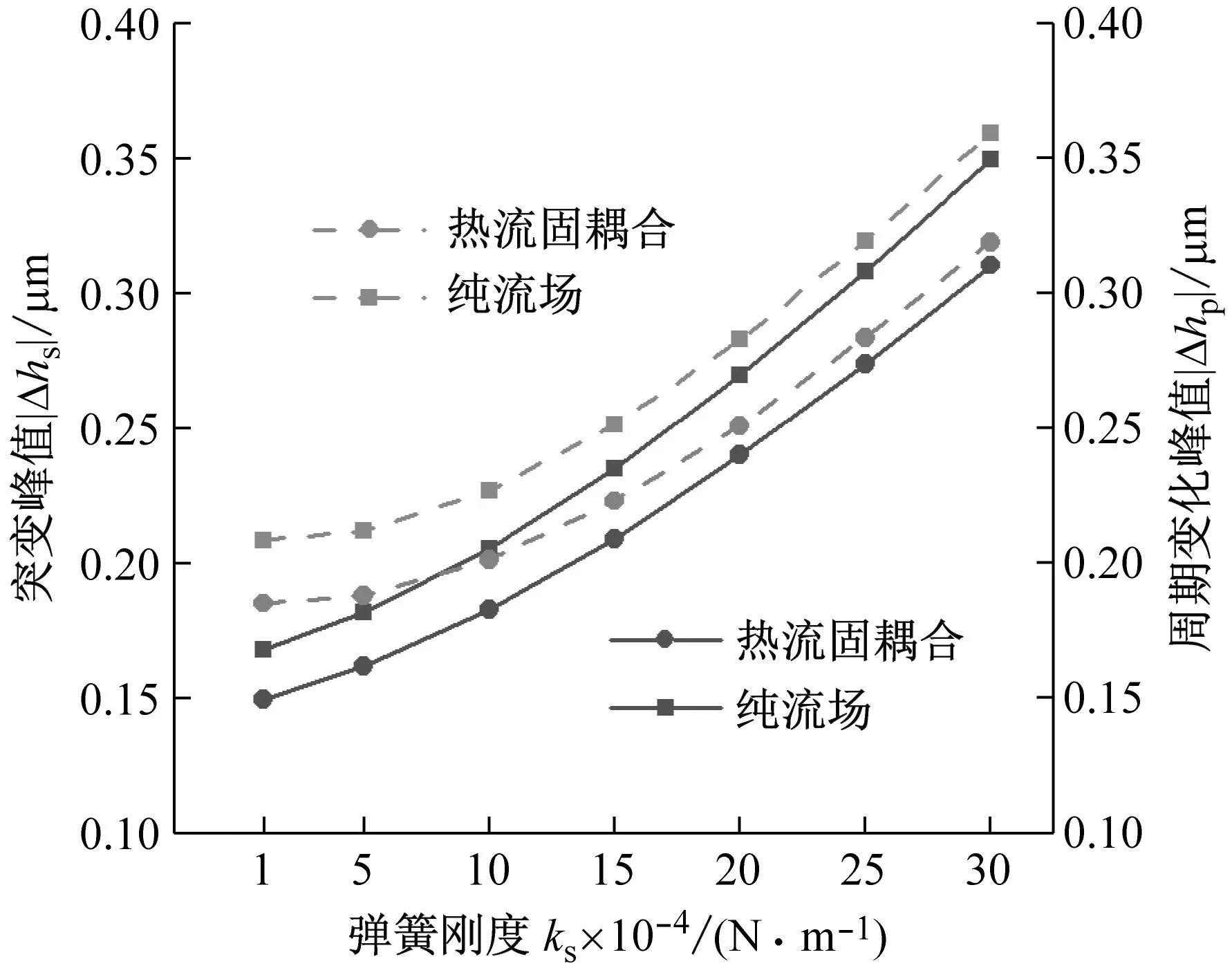
(b) 扰动峰值图11 弹簧刚度对密封动态追随性的影响Fig.11 Effect of spring stiffness on dynamic following performance of seal

(2) O型圈阻尼对密封动态追随性的影响

如图12所示,增大O型圈阻尼同样削弱了补偿环补偿空间,补偿环补偿能力下降,扰动响应增大。极限条件下O型圈阻尼无穷,补偿环补偿能力为零。单独从密封动力学角度来看,液膜密封选用的辅助密封圈的阻尼过大不利于液膜密封的动态追随性。此外热流固耦合模型下的动态追随性优于纯流场模型下的动态追随性,符合前文论述。

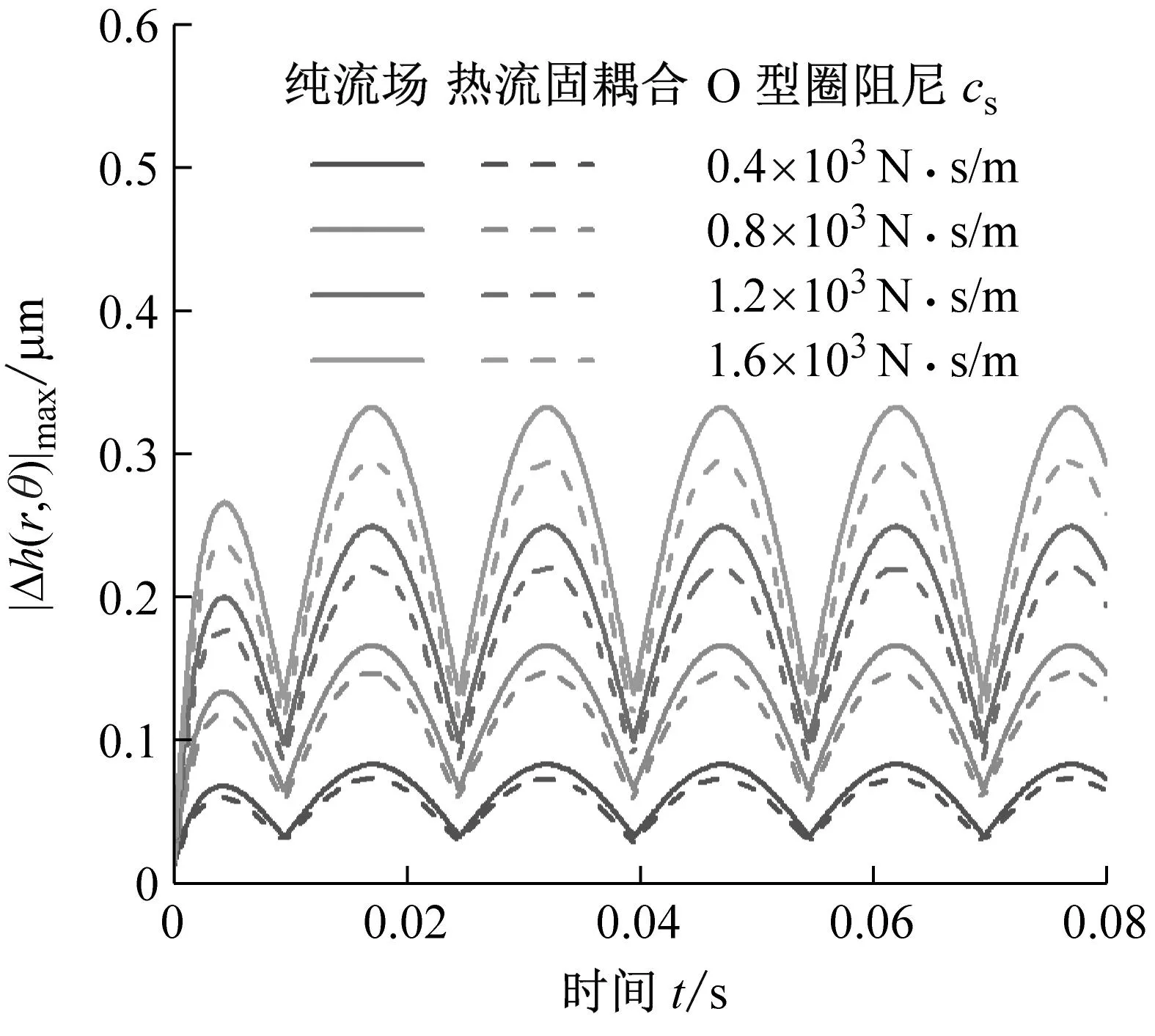
(a) 最大膜厚扰动量

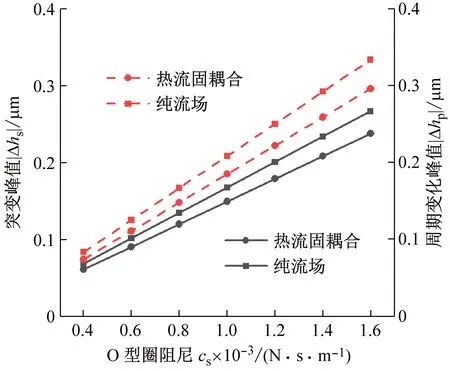
(b) 扰动峰值图12 O型圈阻尼对密封动态追随性的影响Fig.12 Effect of O-ring damping on dynamic following performance of seal

2.5 操作参数对动态追随性的影响

(1) 转速对密封动态追随性的影响

如图13所示为转速n对密封动态追随性的影响。由图可知热流固耦合模型下液膜扰动更小且扰动随转速增加而增加。这是由于转速增大后,液膜动态特性系数减小造成的,故液膜动态特性系数变小,使端面密封的最大膜厚扰动量增大,不利于液膜密封的动态追随性。

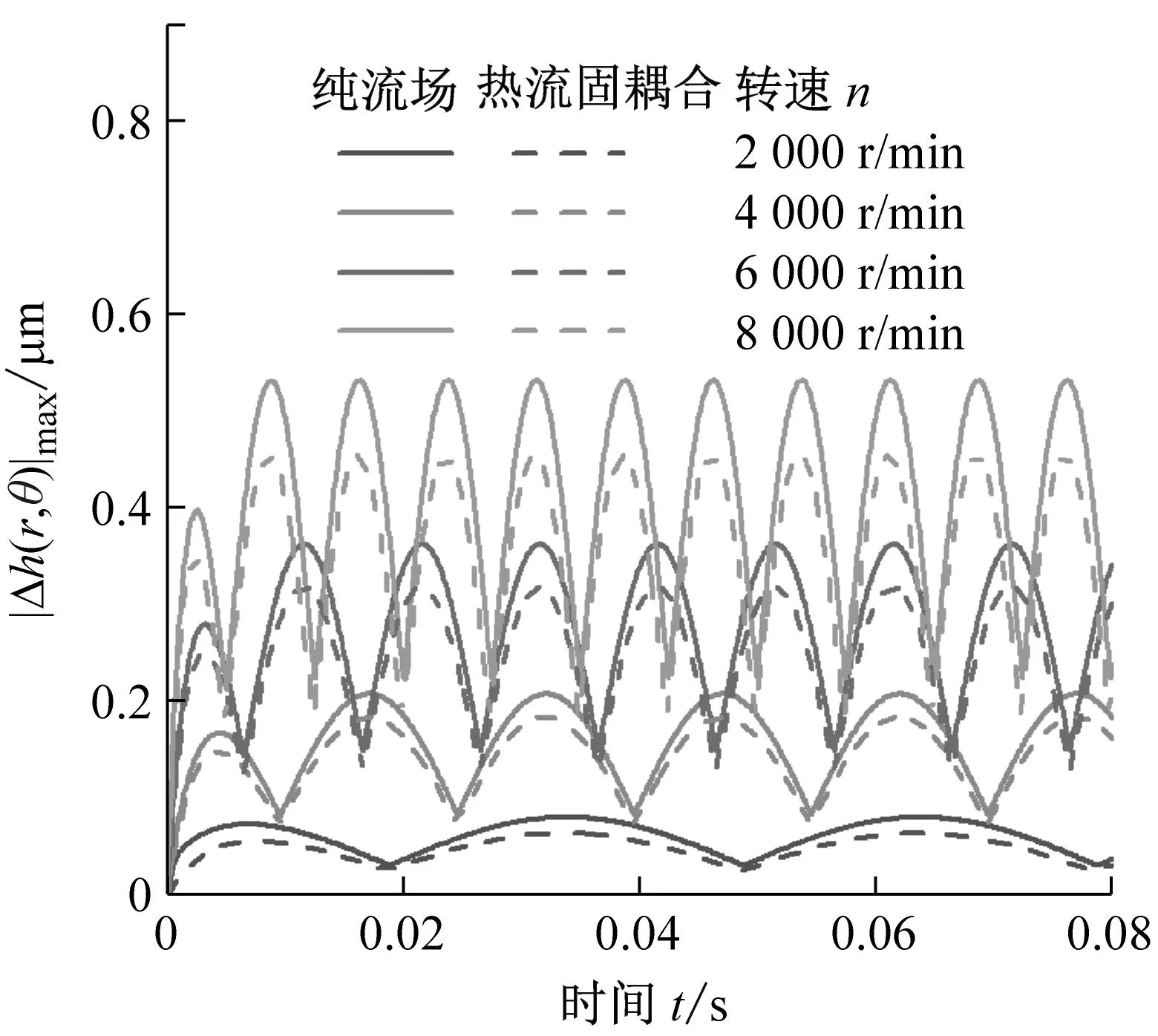
(a) 最大膜厚扰动量

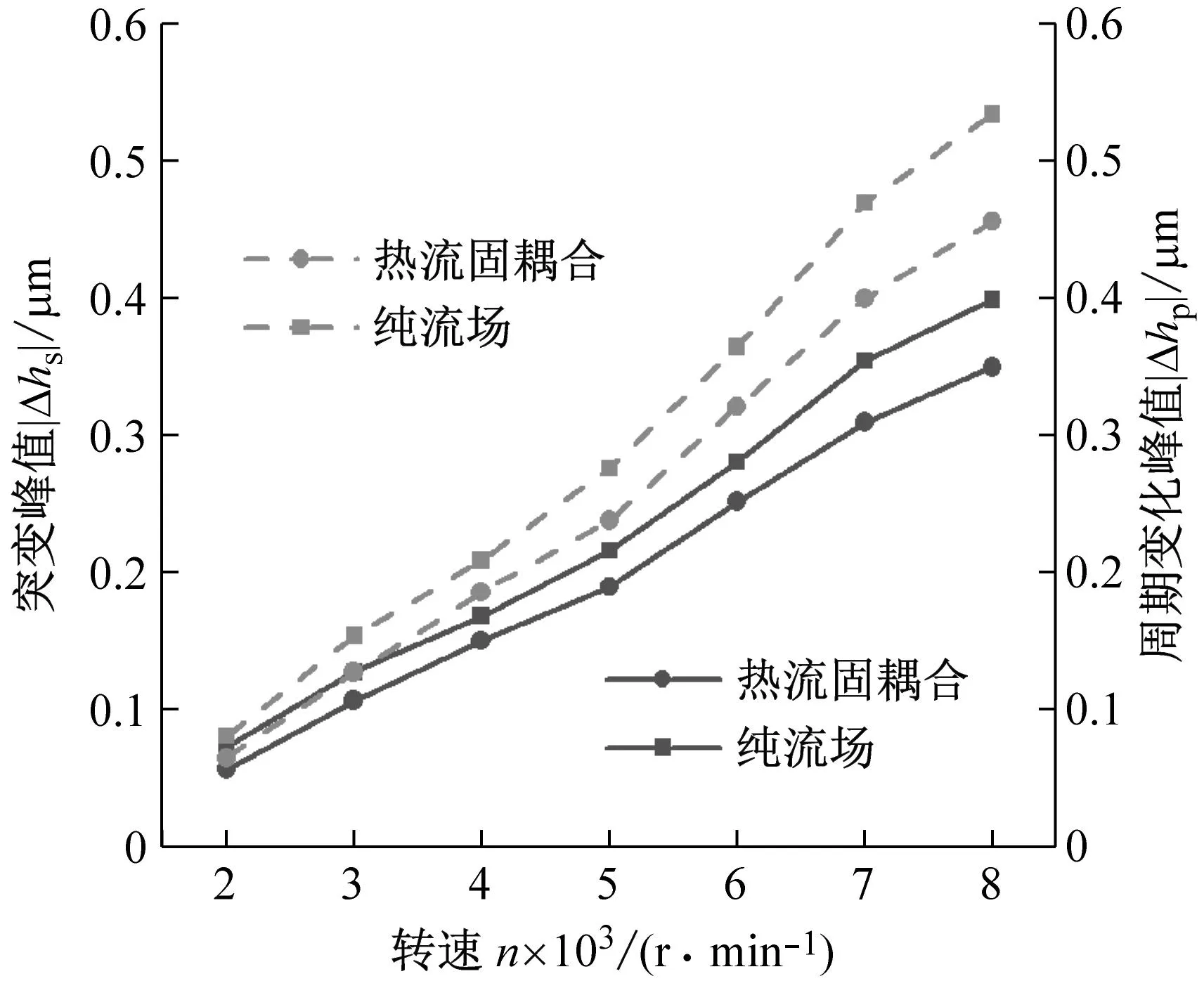
(b) 扰动峰值图13 转速对密封动态追随性的影响Fig.13 Effect of rotating speed on dynamic following performance of seal

(2) 介质压力对密封动态追随性的影响

如图14所示为介质压力po对密封动态追随性的影响。由图可知热流固耦合模型下液膜扰动更小且扰动随介质压力增加而减小。这是由于介质压力的增大,动态特性系数变大,使端面液膜膜厚最大扰动量不断减小。此时增大介质压力,有利于提高液膜密封的动态追随性。

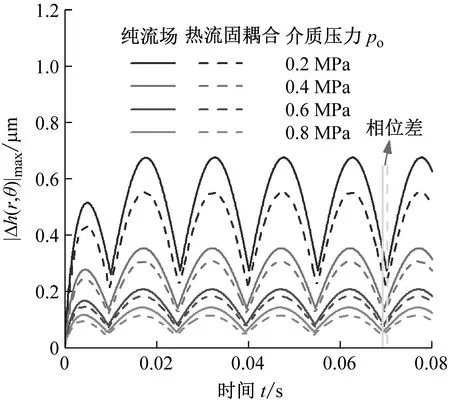
(a) 最大膜厚扰动量

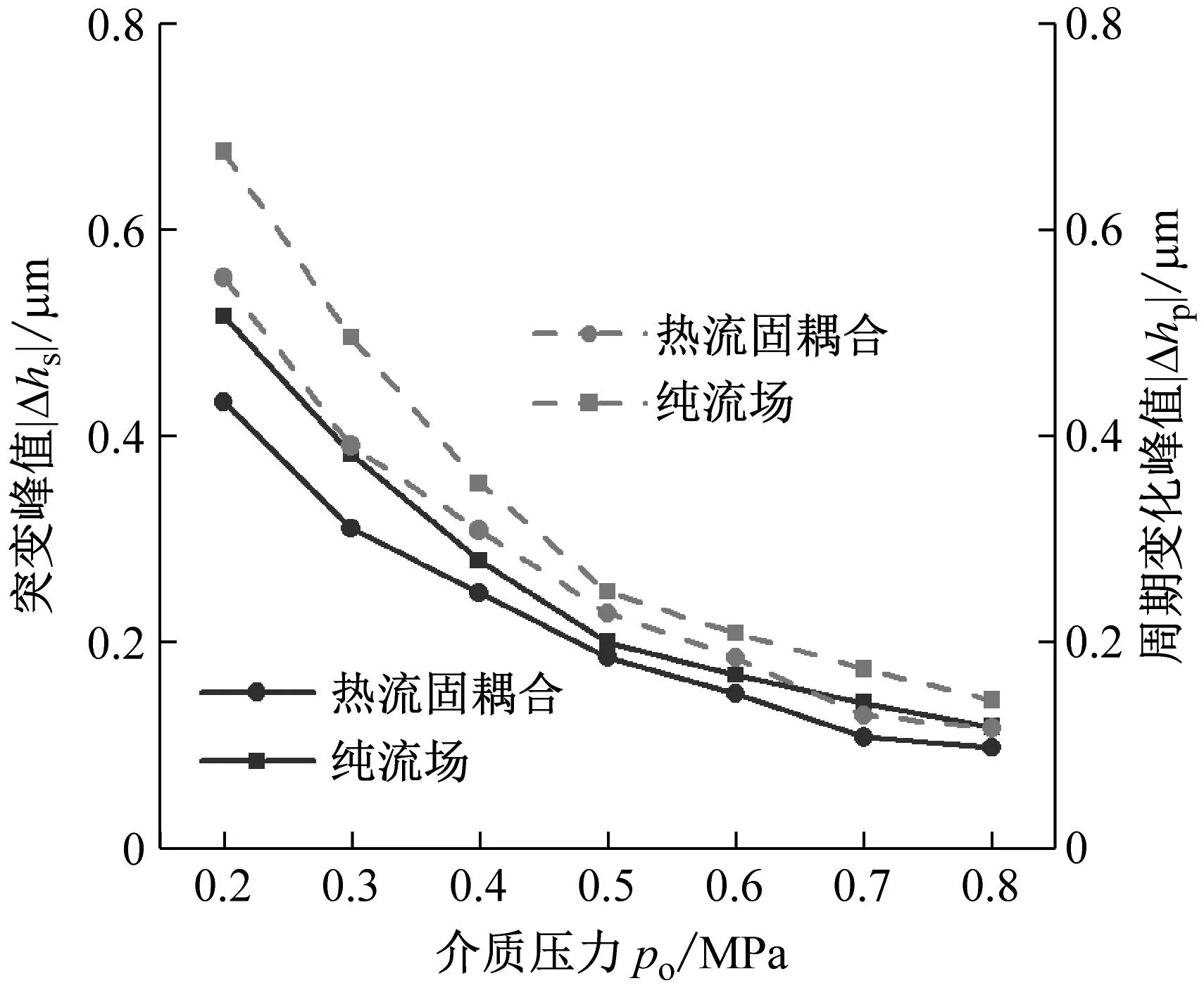
(b) 扰动峰值图14 介质压力对密封动态追随性的影响Fig.14 Effect of medium pressure on dynamic following performance of seal

2.6 结构参数对动态追随性的影响

为分析结构参数对液膜密封动态追随性的影响,利用控制变量法,计算纯流场和热流固耦合两种计算模型。

如图15所示为不同结构参数对液膜密封动态追随性的影响。由图15可知,热流固耦合模型下液膜扰动更小。扰动随槽数增加而增加,随槽深、槽坝比和螺旋角增加而先增加后减小。故增加槽数不利于提高液膜密封动态追随性。在给定参数下,液膜密封动态追随性分别在槽深17 μm,槽坝比0.8,螺旋角22°时达到最优。

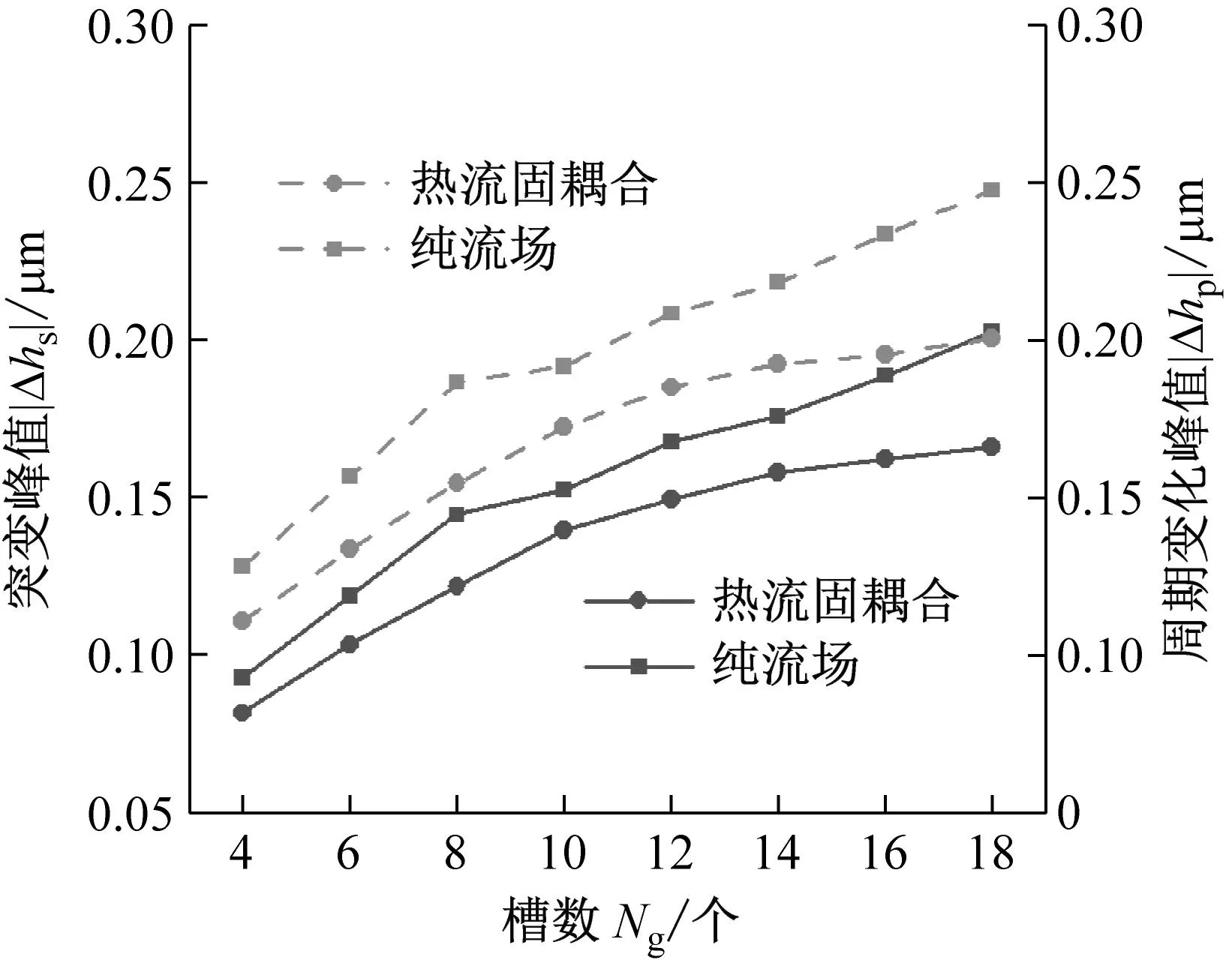
(a) 槽数

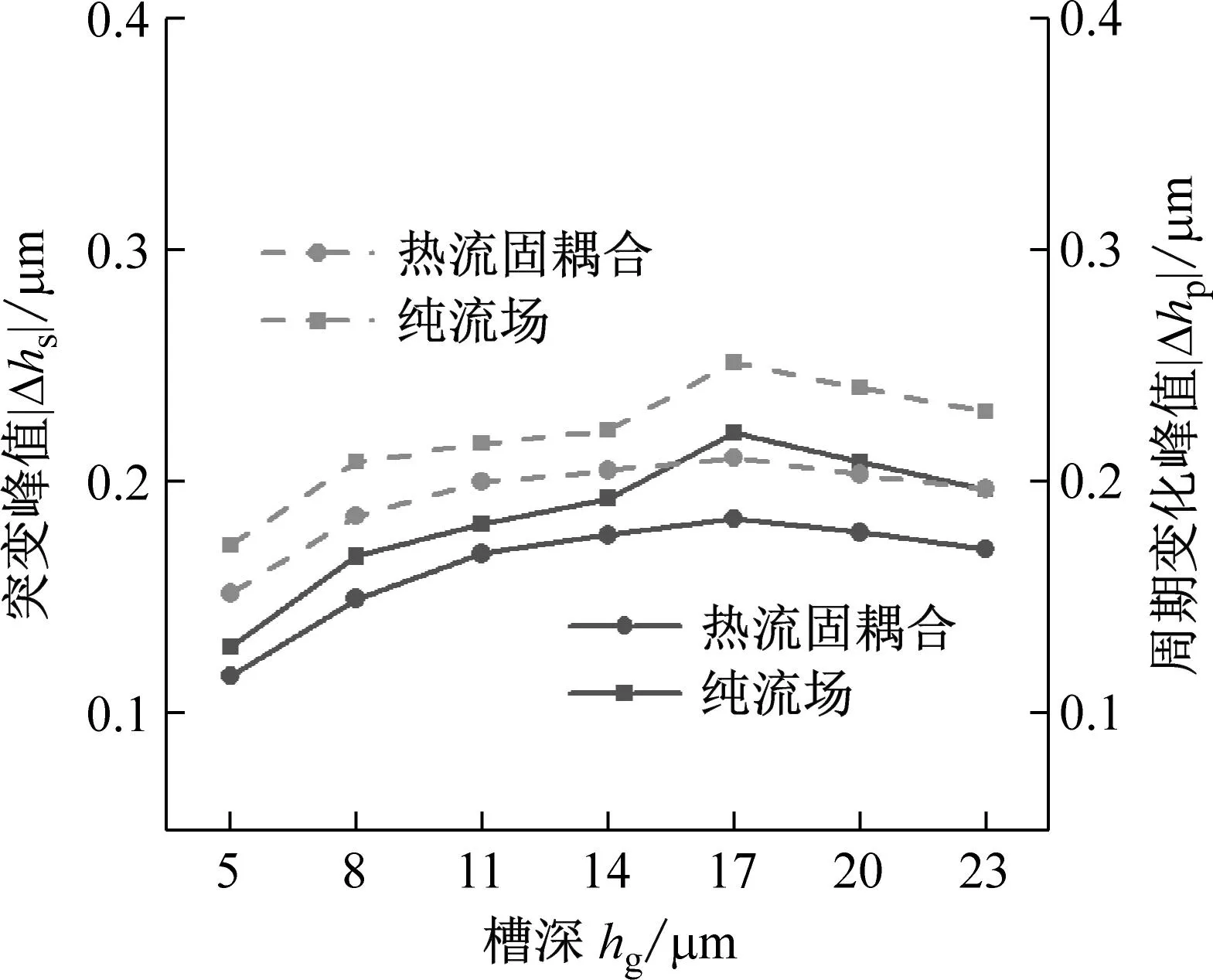
(b) 槽深

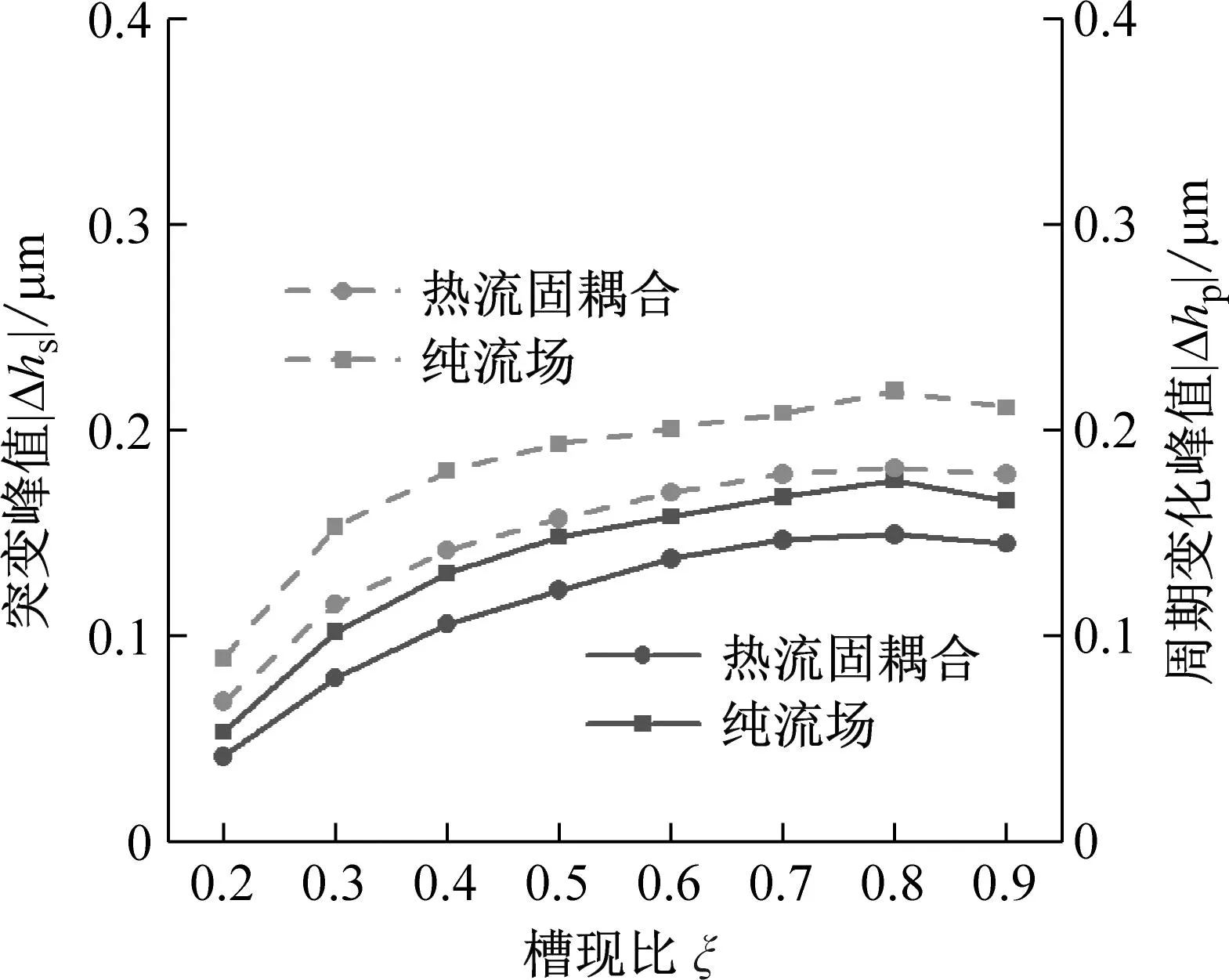
(c) 槽坝比

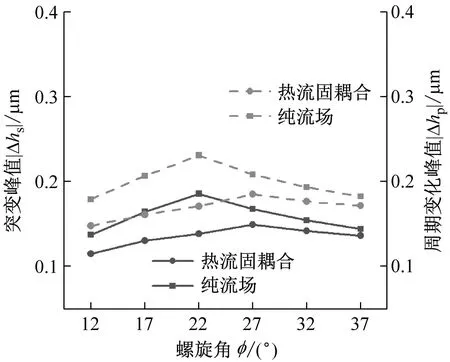
(d) 螺旋角图15 结构参数对密封动态追随性的影响Fig.15 Effect of structural parameters on dynamic following performance of seal

3 结 论

(1) 对比分析了纯流场与热流固耦合条件下,三自由度扰动运动,并利用液膜的最大扰动量时变曲线规律,反映液膜密封的动态追随性。由于热弹变形与黏温效应,热流固耦合条件下,液膜密封动态追随性表现更好。

(2) 对比分析不同激励振幅,不同力学元件参数对动态追随性的影响,发现无论是增加密封轴向、角向激励振幅,还是增加弹簧刚度或O型圈阻尼均会导致扰动增大,从而使得液膜密封动态追随性变差。

(3) 对比分析不同操作参数对动态追随性的影响,发现减小转速或增大介质压力会导致液膜动态特性系数增大,有利于提高密封的动态追随性;针对不同结构参数的影响,减少槽数会提高液膜密封动态追随性,且在槽数给定时,槽深17 μm,槽坝比0.8,螺旋角22°的结构参数设定会得到更好的动态追随性。