广泛联想 多解探究——对一道“华数之星”试题的解法探究及思考

陆祥雪

（江苏省泰州中学附属初级中学）

解题的核心是把待解决的问题与自己已有的知识经验，尤其是解决类似问题的经验联系起来，进而找到解决问题的思路与方法.解题思路的探寻有三个基本环节：一是观察，即审题，解决任何问题都离不开已知的条件与事实；二是联想，包括激活与重组，创新、创造离不开继承，任何问题的解决都要建立在相关知识与经验的基础上；三是预见，包括猜想与转化.联想指由眼前所感知的信息，激活大脑中存储的相关信息，创造性地提出新的信息组合的思想活动过程.联想既是重组信息、用好信息的关键，也是形成直觉、产生预见的关键，这表明了联想在化归中的作用.而解题的实质就是一个不断化归的过程.从不同的角度观察，形成广泛的联想，可以得到多种解决问题的方法.

本文以某次“华数之星”青少年数学大会数学水平测试中的一道四级试题为例，从待求结论、已知条件、图形特征等方面入手进行广泛联想，形成多种解法，以充分体现联想思维在数学解题中的重要作用.

一、题目呈现

题目如图1，在△ABC中，∠A=60°，∠ABC=80°，点I为△ABC的内心，连接BI，CI.求证：CI=AB.

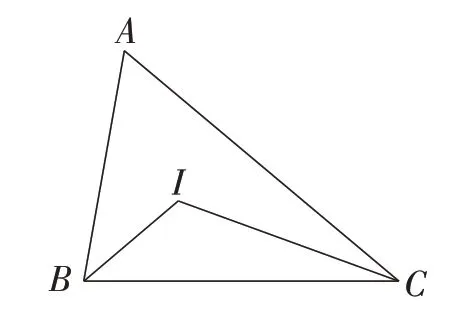
图1

由已知，可得下列结论：①∠ACB=40°；②∠ABI=∠CBI= 40°；③∠ACI= ∠BCI= 20°；④∠BIC= 120°.（以上结论在下面的证明中可以直接应用.）

二、广泛联想

联想1：三角形中边与角之间的关系.

题目给出的条件都是关于角的，但结论是要证明边相等.解决问题的方法是将条件与结论联系起来，于是思考三角形中边与角之间的关系是解题的首选方案.在初中所学的知识范围内，学生容易想到直角三角形边角之间的关系.运用差异分析法，发现需要作垂线来构造直角三角形.于是得到解法1.

解法1：如图2，过点B作BF⊥AC于点F，过点C作CE⊥BI，交BI的延长线于点E.

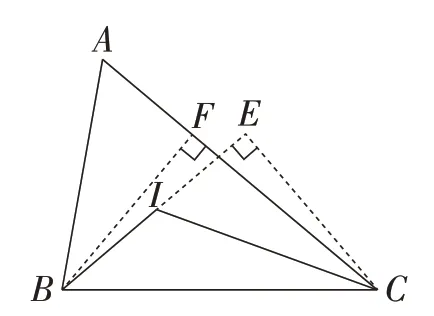
图2

在Rt△ABF中，

因为∠CIE=∠IBC+∠ICB，所以∠CIE=60°.

在Rt△ICE中，

因为在Rt△BCF中，BF=BCsin∠FCB=BCsin 40°，

在Rt△BCE中，CE=BCsin∠EBC=BCsin 40°，

所以BF=CE.

所以AB=CI.

事实上，若运用高中阶段的正弦定理解此题，会更加便捷，但是此知识不在《义务教育数学课程标准（2022年版）》要求的范围内，故在此不作介绍，读者可自行尝试.

初中阶段证明线段相等的方法比较多，常用的有三角形全等、等角对等边、平行四边形的性质、圆中两条弧与弦之间的关系等.

联想2：构造全等三角形.

若想通过三角形全等证明CI=AB，则需要寻找分别包含CI和AB的两个三角形全等.图中现有的△ICB和△ABC并不全等，故可以考虑构造分别含有CI，AB的全等三角形.以当前已知的△ICB或△ABC为基础进行构造是考虑之一，相当于将其中一个三角形剪贴到另一个三角形的位置，剪贴时将相等的边重合或相等的角重合，这样考虑构造的方向比较明确.具体而言，要证IC=AB，可以考虑以IC为一边构造三角形与△ABC全等.

分别将点A与点I、点B与点C对应，在IC上方构造三角形与△ABC全等，可得解法2.

解法2：如图3，过点C作BA的平行线，交BI的延长线于点D，可得∠D= ∠ACB，∠DIC= ∠A，CD=CB.即可得△IDC≌△ACB.所以IC=AB.

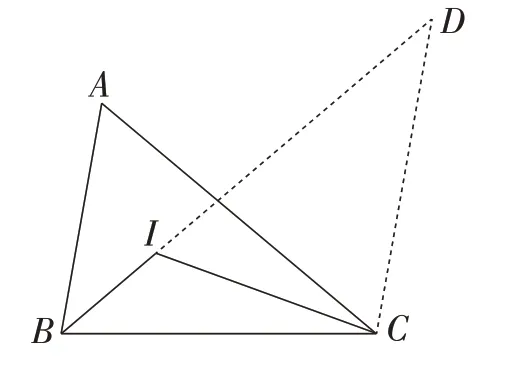
图3

分别将点A与点I、点B与点C对应，在IC下方构造三角形与△ABC全等（实际上是将图3中的△ICD沿IC翻折而成），可得解法3.

解法3：如图4，以BC为边在BC下方作等边三角形BCD，连接ID，可得B，D，C，I四点共圆.所以∠DIC= ∠DBC= ∠A= 60°.因为∠DCI= ∠ABC= 80°，CD=BC，所以△IDC≌△ACB.所以CI=AB.

图4

分别将点A与点C、点B与点I对应，在IC下方构造三角形与△ABC全等，可得解法4.

解法4：如图5，分别过点C和点I作直线IB，AB的平行线，交于点D，ID与BC交于点M，可得∠DIC=∠ABC，∠DCI= ∠A，ID=BC.所以△IDC≌△BCA.所以IC=AB.

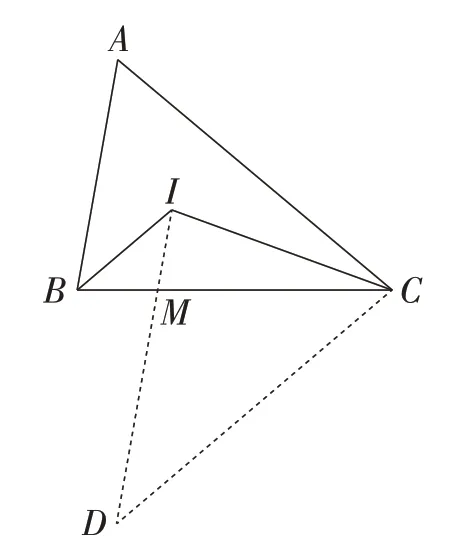
图5

同理，可以以AB为边构造三角形与△IBC全等.

分别将点A与点I、点B与点C对应，在AB左侧构造三角形与△IBC全等，可得解法5.

解法5：如图6，以点B为顶点在△ABC外作∠ABD=20°，交CA的延长线于点D，可得∠BCI=∠ABD，∠IBC=∠D，BC=BD.所以△ICB≌△ABD.所以IC=AB.

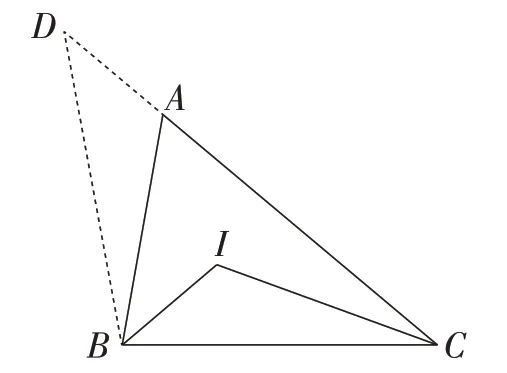
图6

分别将点A与点I、点B与点C对应，在AB的右侧构造三角形与△IBC全等，可得解法6.

解法6：如图7，作∠ABI的平分线交△ABC的外接圆于点D，连接CD，AD，可证得△BCD是等边三角形.所以BC=BD.又因为∠IBC= ∠ADB，∠ICB=∠ABD，所以△ICB≌△ABD.所以IC=AB.

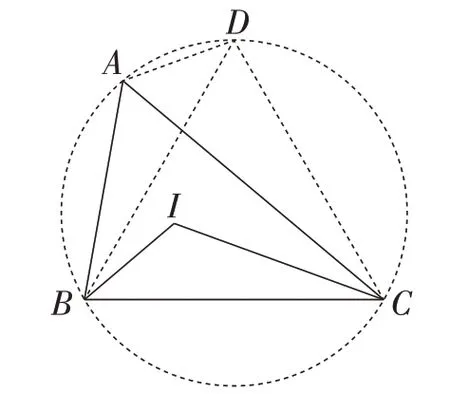
图7

根据∠A=60°，∠BIC=120°，联想到∠BIC的外角与∠A相等，考虑到要证明IC=AB，故作垂线构造全等三角形，可得解法7.

解法7：如图8，过点B作BF⊥AC于点F，过点C作CE⊥BI，交BI的延长线于点E，可以证得△CBE≌△BCF.所以CE=BF.因为∠CIE= ∠A= 60°，所以△ICE≌△ABF.所以IC=AB.

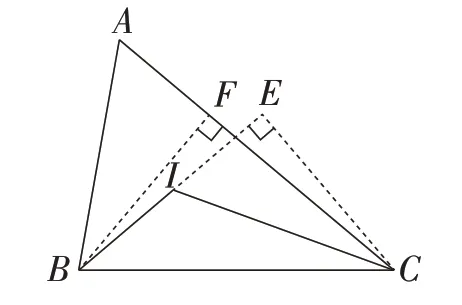
图8

联想3：利用60°角构造等边三角形，转化线段证明全等.

在要证明的相等线段所在的三角形不全等的情况下，可以考虑先等量代换，再证明三角形全等.由60°角联想到等边三角形，从而转化线段.由∠A=60°及∠BIC的邻补角等于60°，可得解法8和解法9.

解法8（转化AB）：如图9，在AC上截取AD=AB，连接BD，则△ABD是等边三角形.所以∠BIC=∠BDC=120°，∠ICB=∠DBC.又因为BC=CB，所以△ICB≌△DBC.所以IC=BD.所以IC=AB.

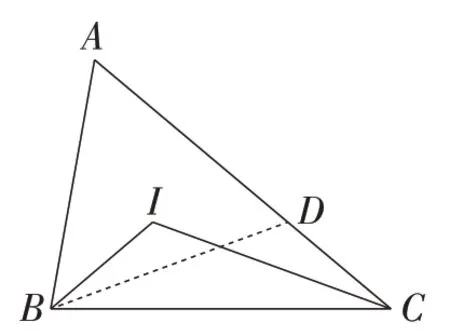
图9

解法9（转化IC）：如图10，延长BI到点D，使ID=IC，连接CD，则可得△ICD是等边三角形.所以∠D=60°，∠BCD=80°.所以∠D=∠A，∠BCD=∠ABC.又因为BC=CB，所以△DBC≌△ACB.所以DC=AB.所以IC=AB.

图10

联想4：平移汇聚转化.

由于AB，IC，∠A，∠BIC的位置比较分散，联想到通过几何变换可以使分散的线段、角集中，故考虑利用平移将线段AB，IC汇聚到一起，可得解法10.

解法10：如图11，分别过点B，C作AC，AB的平行线交于点D，则四边形ABDC为平行四边形.在BD上截取BE=BI，连接CE.可证得△EBC≌△IBC.所以EC=IC，∠BEC= ∠BIC= 120°.所以∠DEC= 60°.又因为∠D=∠A=60°，所以△CDE是等边三角形.所以CD=EC=AB.所以IC=AB.

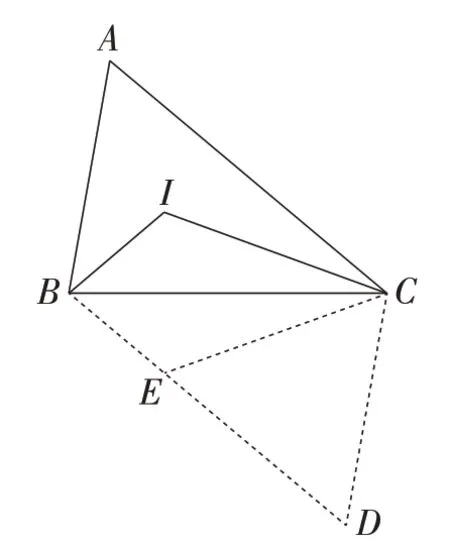
图11

上面的证法是联想角的轴对称性，也可以联想角平分线的性质.如图12，过点C分别作BD，BI的垂线，垂足分别为点E，F，证明过程略.

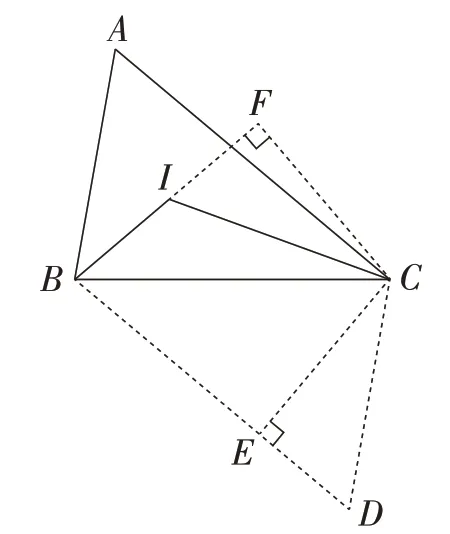
图12

解法10 中，将∠A与∠BIC汇聚到一个四边形中后，因为∠BIC+∠D=180°，所以联想到B，D，C，I四点共圆，也可以证明.证明过程略.

联想5：圆中的等量关系.

我们知道在同圆或等圆中，弧、弦、圆周角、圆心角中的一组量相等，其余对应的量也相等.尽管看似转化跨度较大，但注意到∠IBC= ∠ACB，若作△ABC的外接圆，则可联想到“在同圆中，相等的圆周角所对的弦相等”，所以不妨探索一下.

解法11：如图13，作△ABC的外接圆，延长BI交圆于点D，连接CD，可证得△CDI是等边三角形，得CD=IC.因为∠DBC=∠ACB=40°，所以CD=AB.所以IC=AB.

图13

上述5 种联想的方向主要集中在两个方面.一是条件、结论间的联想，如联想1和联想4都是为了充分沟通条件与结论；二是对解题方法的联想，如联想2中的全等三角形的构造是以一个三角形为基础，结合图形位置进行变换，联想3是先转化再证全等，联想5是由直线型问题转向曲线型问题，更能体现思维的广阔性.这些都体现了广泛联想的信息源.对不同信息源的联想，衍生出不同的问题解决方案，能够促进学生思维的深刻性和广阔性.

三、几点思考

1.问题的本质

在讲授两个三角形全等的条件时，我们知道“有两边及一边的对角分别相等的两个三角形不一定全等”.在这两个三角形不全等的情况下，两个三角形中另一组相等的边所对的角互补.其逆命题是：（1）在两个三角形中，若有一组角相等，有一组边相等且其对角互补，则相等的角所对的边相等；（2）在两个三角形中，若有一组边及其对角相等，有一组边的对角互补，则互补的这对角所对的边相等.这两个命题均是真命题.如图14，我们将图1 分解，则可以看作是上述逆命题的具体化.这说明原题的很多解法是由两个三角形的特殊位置得来的.

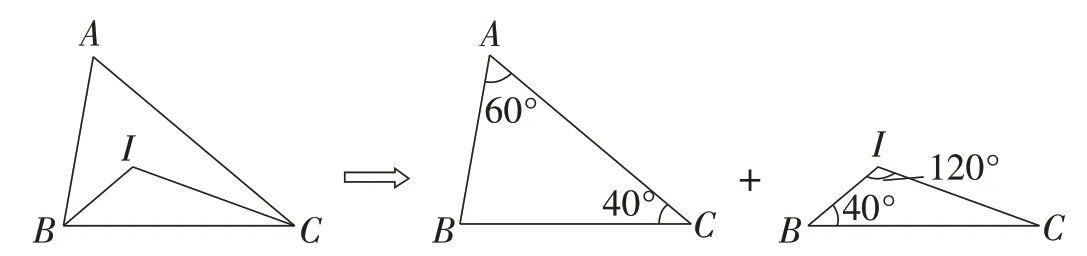
图14

溯源问题，基于联想，是对类似问题的联想.对问题中图形的抽象，是抽象能力和空间观念的体现，是数学眼光的主要表现之一；探讨问题，是推理意识或推理能力的体现，是数学思维的主要表现之一；表达问题，归于常见模型，是模型观念的体现，是数学语言的主要表现之一.这些均是数学课程要培养的数学核心素养.

2.联想的实现

联想是以观察为基础，根据研究的对象或问题的特点，联系已有的知识和经验进行想象的思维方法.联想是一种自觉的、有目的的想象，是由当前感知或思考的事物，想起有关的另一事物，或由此想起其他事物的心理活动.数学问题通常涉及数、式、图形等，解决数学问题需要以“四基”为工具.那么，如何实现广泛联想，以储备丰富的数学基础知识、基本技能、基本思想、基本活动经验呢？掌握数与式的结构、基本图形的特征等是必要的前提.题目中要求证明线段相等，那么如何证明线段相等呢？由此展开联想，联想的网能张多大，取决于学生对证明线段相等方法的积累有多少.由60°角可以得到哪些结论？哪些图形与60°角相关？由两角互补又能想到什么？四点共圆呢？学生若能养成解决问题后反思的习惯，反思条件、解法、结论、解题过程等，则会增加对知识和经验的积累，从而在联想、发散、聚合的循环中不断增加自身的知识储备.

3.多解的意义

解决问题从观察开始，由对问题中触发思维联想点的不同思考，就会产生不同的解法.一题多解，能培养学生的发散性思维、求异性思维和创造性思维，还能更多、更广地运用所学的知识、思想和方法；能促进学生养成解题后进行反思回顾的习惯，培养学生的元认知能力；能使学生的解题从表层走向深入，从零散走向系统，为解题教学提供新的角度.学生在这个过程中逐步提升高阶思维，对数学学习有更深刻的认识和体验，理解数学本质，发展数学核心素养.

教师要积极鼓励并正确引导学生进行一题多解.学生只有意识到了一道题是可以有多种解法的，就会自然而然地对一题多解产生兴趣，从而提升解决问题的能力.

联想既是数学解题的一种习惯、一种策略、一种方法，也是有效发展学生思维能力的一种策略、一种载体、一种手段.数学解题教学应该通过加强联想教学，促进学生品性、心智、知识与技能的协调发展.广泛联想能促进一题多解，反过来，一题多解又能增加联想的思路.