建构之本 始于关联
——以“二次函数的图象和性质”单元教学为例
周海东,蒋妍兮
(江苏省苏州工业园区星洋学校;西安交通大学附属苏州初级中学)
数学核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力,以及情感、态度和价值观的综合体现.传统的课时教学比较关注基础知识、基本技能的习得,这种碎片化的数学学习方式有利于夯实基础,熟练技能,但却无法将知识蕴含的数学本质表述清楚,更无法体现数学核心素养的培养.开展基于发展学生数学核心素养的教学,教师需要以教材为基础,用系统论的方法对教材中具有某种内在关联的内容进行分析、重组、整合,形成相对完整的教学单元,在整体观的指导下将教学诸要素有序规划.这样就能让学生在关注知识技能的同时,思考知识技能所蕴含的数学本质,体悟知识中蕴含的数学思想,从而促进学生数学核心素养的形成与发展,达到学科育人的目的.本文以苏科版《义务教育教科书·数学》九年级下册“二次函数的图象和性质”这一内容为例,基于系统分析的视角,从发展学生数学核心素养的目标出发,把握教材内容之间的关联,对教学内容进行重新建构,进行单元教学设计.现将本节课的建构过程进行呈现,以期为培养初中学生数学核心素养的研究提供借鉴.
一、教学内容分析:用系统的观点建构课堂教学体系
系统的观点也就是整体的观点、联系的观点,即要素与要素、要素与相关要素、要素与环境之间的关系.运用系统的观点分析二次函数的图象与性质:要素是二次函数表达式的系数和函数的图象;相关要素是自变量与函数值之间的关联,二次函数表达式之间的关联,以及它们所对应的图象之间的关联;环境是教学目标的定位、教学策略的选择,以及学生已有经验之间的关联.从宏观视角来看,二次函数是学生在初中阶段学习的最后一个代数函数,是描述现实世界数量关系的重要数学模型,其内容蕴含“变化与对应”的函数思想.从中观视角来看,用运动变化的观点,采用从特殊到一般的路径、数形结合的方法探索二次函数y=ax2+bx+c(a≠0)的图象和性质是二次函数的核心内容,也是应用二次函数知识解决相关问题的基础.从微观视角来看,教材安排了4个课时,分别研究y=x2及y= -x2,y=ax2,y=ax2+c及y=a(x+h)2,y=ax2+bx+c的图象及它们之间的关系,但这四个具体内容在研究方法、研究路径、图象与性质方面又具有一致性,这样我们就能从系统的观点来建构本节课的教学体系(如图1).

图1 “二次函数的图象和性质”教学体系
二、教学结构分析:用区块链的结构形成学习路径
从哲学的视角来看,特殊与一般既对立又统一.一般包含了特殊,比特殊更能反映事物的本质;而与一般相比,特殊往往显得简单和容易,直观和具体.因此,从内在结构来看,二次函数y=ax2+bx+c(a≠0)的图象与y=x2,y=x2+ 1,y=(x+1)2图象之间体现了这种辩证关系.而具体到某个特殊的函数,对其图象与性质的研究又是一个相互独立的系统.同时,某个具体函数的图象与性质的研究方法和路径又可以沿用到其他具体的函数,就像科技领域的区块链技术,其研究过程既相互独立又有内在关联,在每个独立的探索过程中都能形成封闭的研究路径,积累的基本活动经验相互关联,逐步推进学生数学关键能力的提升,从而有利于数学核心素养的形成.因此,我们用区块链的结构形成了如图2所示的学习路径.

图2
三、教学过程分析:用数形结合的方法探索函数的性质
图象研究的是图形的结构特征,性质描述的是数量间的变化规律.二次函数是描述客观世界变化规律的重要模型,它的变化特征反映了它所刻画的客观世界变化规律的特征.因此,本节课的教学过程紧扣“数”与“形”,用数形结合的方法探索二次函数的性质.下面呈现探索过程片断.
活动:探索函数y=x2的图象和性质.
问题1:观察表达式,变量x,y的取值有何要求?两个变量之间有怎样的变化规律?
问题2:你能猜想一下函数y=x2的图象有什么特征吗?
【教学说明】研究函数的性质时,我们往往习惯于从图象出发,直观地感受其中的变化规律,却忽略了表达式的重要性.描述一个函数,可以利用表达式、表格及图象三种方式来呈现,且从这三种表达方式都可以看出函数的性质.从“数”出发想象图形的特征,是一个“从数到点再到形”的过程,有利于学生形成对图象特征的构建,从整体上对图象的分布和形态有一个较为清晰的认识,也为接下来的描点作图指明了方向.
师:通过对表达式的分析,我们脑海中对函数y=x2的图象有了一个大概印象.函数y=x2的图象分布在x轴及其上方,关于y轴对称,过原点且原点为最低点,图象从左到右呈现了先下降再上升的趋势.但是符合这些特征的图象有很多,光“想”可能还不够,应该怎么办呢?
学生回答画出图形.
师:回忆之前的学习经验,你能试着画出函数y=x2的图象吗?
操作:学生在透明纸上按下列步骤画出函数y=x2的图象:①列表(如表1);②描点(如图3);③连线.

表1

图3
讨论:图4 和图5 都符合对函数y=x2的图象的猜想,哪种连线方式能反映图象的特征呢?

图4
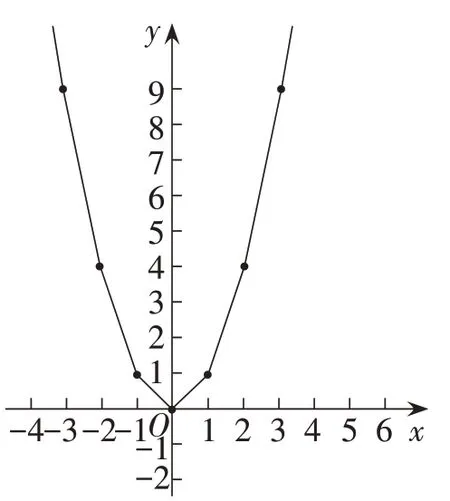
图5
操作:利用几何画板软件改变点的密集程度和点的个数,得图6,再制作一个动点,使得其纵坐标是横坐标的平方,追踪这个动点,观察它经过的路线所形成的图形,如图7所示.

图6

图7
【教学说明】学生对二次函数图象的认识是一个从模糊到清晰最后走向理性的过程.由于画图的局限性,学生在经历了猜想、描点、连线的过程后,能够大致感知图象的特征,但还是无法准确把握图象的形状.“由数想形”无法看到全貌,“描点画图”无法合理解释图象的连续性.因此,这里借助信息技术,通过两个层次的实验来解决图形的直观性和连续性问题,从而让学生真正理解函数y=x2的图象.第一个实验是通过“点加密”来直观观察y=x2的图象,随着点的数量的增加,学生能逐步看清楚图象的形状;第二个实验是通过“点运动”来解释图象的连续性.
四、教学价值审视:在高观点下实现思维的生长统一
函数的性质其实就是变量在变化过程中所表现出的一种对应,这种对应可以被表征为一种“不变性”,而图象就是外显这种不变性的重要工具.回顾函数的发展历史,无论是莱布尼茨从变量的观点提出函数,还是康托尔提出集合、映射的观点,数学家们始终在努力寻找这种变化中的对应.如果能确定变化过程中的不变性,便能对变量的“前世”“今生”“未来”进行确定把握.从“数”的角度无法准确把握的性质,可以通过“形”来表征,对“形”的认识可以从对“点”的研究来找到.同时,借助“形”又可以认识“数”的规律,这也是研究函数图象与性质的一般路径.从学科教学价值的视角来审视课堂,相对知识技能而言,教学更应该重视这种思想方法的渗透.这里对每一个具体函数(y=x2,y=x2+ 1,y= (x+1)2)的学习都用如图8 所示的研究路径去统一,让学生在对具体函数研究的基础上用高观点来形成认识上的统一,进行更高层次的抽象,实现高阶思维的生长.

图8
德国数学家F.克莱因认为,基础数学的教师应该站在更高的视角来审视、理解初等数学问题,只有观点高了,事物才能显得明了而简单.其实,不仅教师的教如此,学生的学也是如此.数学教学的终极目标是让学生理解或掌握研究数学的方法,帮助学生建立学科观念和学科思维.因此,在进行单元教学时,教师只有对教材内容结构有一个系统的、整体的把握,才能在教学设计中实现知识结构的关联,才能使学生学到结构化、联系紧密、迁移能力强的知识;只有把知识置于历史、当下和未来的生活中,用联系的、发展的思维去认识、理解、把握、体验、应用,才能让学生理解、接受、掌握知识的数学本质,真正把握知识的脉络.
教学价值是教学设计的灵魂.核心素养是当前基础教育的育人目标和方向.我们对单元教学的认识可能还不够清晰,对数学核心素养的理解可能还有所欠缺,但我们坚信,这样的教学实践在学生学科关键能力的生成,思维习惯的培养,以及情感、态度和价值观的形成方面一定能发挥独特的作用.

