理解题目明通法 探寻本质显立意——例谈用怎样解题表分析框架评析中考几何压轴题

闻国梁

（浙江省杭州市余杭区五常中学）

2023年中考数学浙江杭州卷最后一题为几何压轴题，以三角形和圆为背景，考查了等腰三角形、直角三角形、圆等基本图形的相关性质，综合性强，对学生来说有一定难度.当遇到比较难的问题时，按照波利亚怎样解题表的四个阶段（弄清问题，拟订计划，实现计划，回顾反思）解题，不仅能产生多种解题思路，使问题迎刃而解，而且可以洞穿问题的本质，举一反三，从而达到“做一题、会一类、通一片”的效果.在解题过程中，以题育人，有助于提高学生系统解决问题的能力，发展理性思维，从而落实立德树人根本任务.

一、呈现题目

题目如图1，在⊙O中，直径AB垂直弦CD于点E，连接AC，AD，BC，作CF⊥AD于点F，交线段OB于点G（不与点O，B重合），连接OF.

图1

（1）若BE=1，求GE的长.

（2）求证：BC2=BG·BO.

（3）若FO=FG，猜想∠CAD的度数，并证明你的结论.

为了聚焦文章的核心内容，略去对第（1）（2）小题的讨论.下文按照波利亚怎样解题表的四个阶段展开对第（3）小题的解法、本质和变式的研究.

二、理解题目

第（3）小题要求猜想∠CAD的度数，并证明结论.此题给出了3 个已知条件：①在⊙O中，直径AB⊥CD；②CF⊥AD；③FO=FG.先对问题进行定性分析，当∠CAD的大小确定时，等腰三角形ACD的形状随之确定，其他图形的形状，以及FG与FO的数量关系也随之确定.

不妨设∠CAD=α，当α>60°时，点G在点O的上方；当α= 60°时，点G与点O重合；当α< 60°时，点G在点O的下方.因此，我们可以确定α<60°.当α的度数由小到大变化时（0°<α<60°），∠FGO的度数逐渐减小（60°<∠FGO<90°），∠FOG的度数逐渐增大（0°< ∠FOG< 120°）.所以必存在一个α的值，使得∠FGO=∠FOG.反之，当FO=FG时，亦可以求得∠CAD的度数.同时，学生可以用量角器测量∠CAD的度数并大胆地提出猜想，进而通过作图来验证猜想.

由条件①可以得到∠CAB=∠DAB，由条件②可以得到∠DCF=∠DAB，由条件③可以得到∠FOG=∠OGF.综上分析，可知图中相等的角主要有三类，即∠CAB=∠DAB=∠DCB=∠DCF=，∠CAD=∠BCG=∠OFG=α，∠FOG= ∠OGF= ∠CGB= ∠CBG= ∠D= ∠ACD=；平行线有FO∥BC；相似的三角形有△FOG∽△CBG∽△ACD.

题目所给的3 个已知条件所蕴含的隐性条件十分丰富，这些条件在后续的解题思路中均直接使用，不再赘述.

三、拟订方案

此题主要考查的是三角形和圆的相关知识，因此在问题解决时应该聚焦三角形边角之间的关系及圆的轴对称性和旋转对称性的讨论.

解题的成功与否取决于选择的角度，也取决于能否从容易接近的一侧来攻克要塞.在平时解题时，遇到此类求角度的问题通常采用以下两种解决方案.

第一，聚焦条件中角度间的关系.从此题中所给的角度的数据出发，可以结合三角形、圆中有关角的性质进行求解.三角形中关于角的性质有三角形的内角和及外角的性质，圆的轴对称性主要体现在垂径定理上，旋转对称性主要体现在圆心角、弧、圆周角三者间数量关系的转化上.于是将求角度问题转化为探寻圆与三角形中相关角之间的关系.

第二，聚焦条件中线段间的数量关系.在直角三角形中，根据锐角三角函数的性质可以求出边之间的数量关系，求出三角函数值，从而求出角度.求线段长度常用的方法有勾股定理、面积公式、相似三角形、三角函数等.当问题中没有给出线段长度时，为了便于求解，可以设某条线段的长度为“单位1”.

四、执行方案

1.聚焦条件中角度间的关系

思路1（聚焦FO∥BC的条件）：如图2，延长FO交AC于点H.由已知，得FO∥BC.所以∠AHF=∠ACB=90°.由垂径定理，可知HF垂直平分线段AC，所以△AFC为等腰直角三角形.所以∠CAD=45°.

图2

思路2（将角转化到圆心角上）：如图3，连接OC，可得∠AOC=180°-∠BOC=180°-α，∠COF=∠COG+∠GOF= 90°+，∠AOF= 360°- ∠AOC- ∠COF=90°+所以∠AOF= ∠COF.又因为OA=OC，OF=OF，所以△AOF≌△COF.所以AF=CF.从而求得∠CAD=45°.

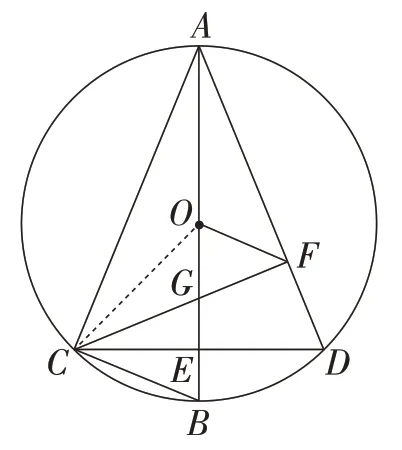
图3

思路3（将角转化到圆周角上）：如图4，延长CF交⊙O于点P，连接AP，OP.根据圆周角定理，可得∠DAP= ∠DCP= ∠BAD.因为∠AFG= ∠AFP= 90°，AF=AF，所以△AFG≌△AFP.所以FP=FG=OF.所以∠GOP=90°.从而求得∠CAD= 45°.也可以证A，O，F，P四点共圆，从而得到∠AOP=90°.

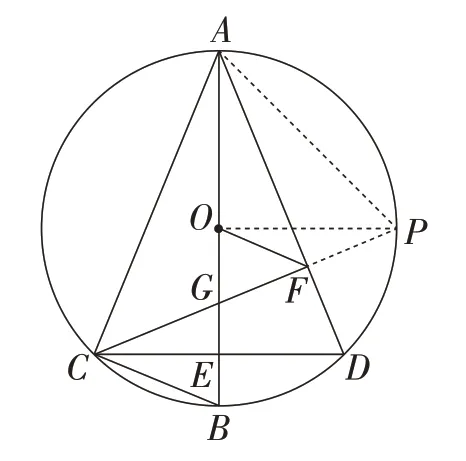
图4

思路4（将角转化到四边形COFD上）：如图5，连接OC，OD.由分析可知，∠OCD=90°-α，∠DFO=90°+α，即∠OCD+ ∠DFO= 180°.所以C，O，F，D四点共圆.所以∠COD=∠CFD=90°.所以∠CAD=45°.

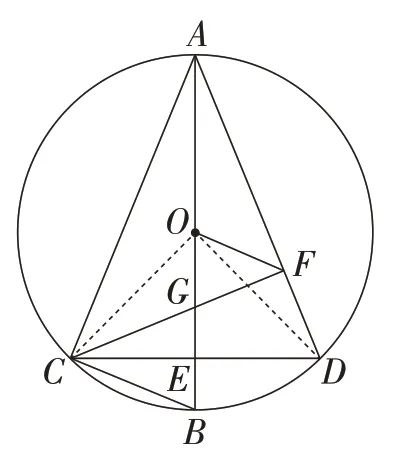
图5

2.聚焦条件中线段间的数量关系

不妨设⊙O的半径为“单位1”，OE=k.如图6，连接CO，可得∠COE= ∠CAD=α.则在等腰三角形BCG中，可得GE=BE=1-k，BG=2-2k，OG=OB-BG=2k-1，聚焦线段间的数量关系，根据勾股定理、相似三角形、锐角三角函数的性质即可求解.

图6

思路5：如图7，过点G作GH⊥AC于点H.在Rt△ACF中，因为AG平分∠CAF，所以GH=GF.所以因为△OGF∽△BGC，所以即解得所以α=45°.

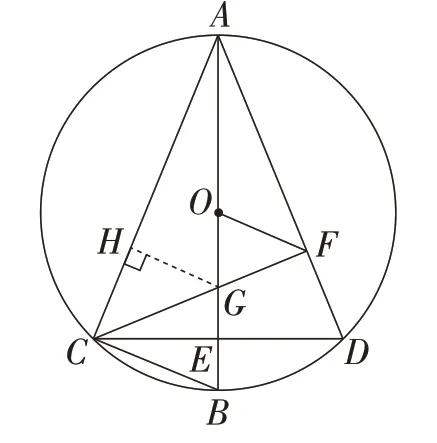
图7

思路6：如图8，过点F作FI⊥AB于点I，可得，AE= 1 +k.因为IF∥CD，所以△AIF∽△AED.所以即解得所以α=45°.

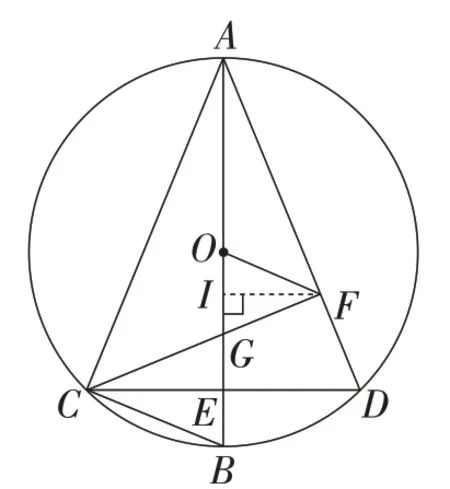
图8

思路7：如图8，过点F作FI⊥AB于点I，可得△GIF∽△GEC.所以所以IF=kCE=.结合已知可得△AIF∽△FIG.所以，即IF2=IG·AI.所以解得所以α=45°.

五、回顾反思

1.探寻本质

一个好的数学问题，问题的本质要有深度，结论具有可推广性.回顾题目中的图形，“做减法”去除辅助图形，探寻本质.如图9，原题中的点G为等腰三角形ACD的垂心，延长FO交AC于点H，根据FO=FG，证明得到FH⊥AC；作点F关于直线AE的对称点F′，可知点O为△AFF′的垂心.于是将图1 中的以AB为直径的⊙O及BC，BE去掉，问题的本质即探究等腰三角形ACD和等腰三角形AFF′垂心之间的关系.

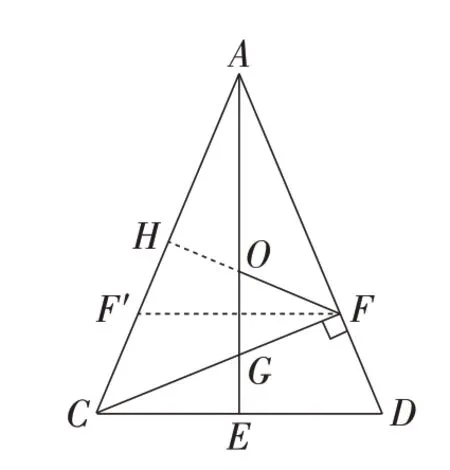
图9

为了便于探究垂心间的关系，我们将符号进行统一，将条件进行更一般化的表述.如图10，已知点H0为锐角∠BAC平分线AD上的一点，过点H0作H0P1⊥AB，交AB于点P1；过点P1作P1P2⊥AC，交AC于点P2，交AD于点H1；过点P2作P2P3⊥AB，交AB于点P3，交AD于点H2.按此规律依次作垂线，过点Pn作PnPn+1垂直于角的另一边，交角的另一边于点Pn+1，交AD于点Hn.记点Pn关于直线AD的对称点为Pn′.由作图可知，点Hn为△APnPn′的垂心（n为正整数）.

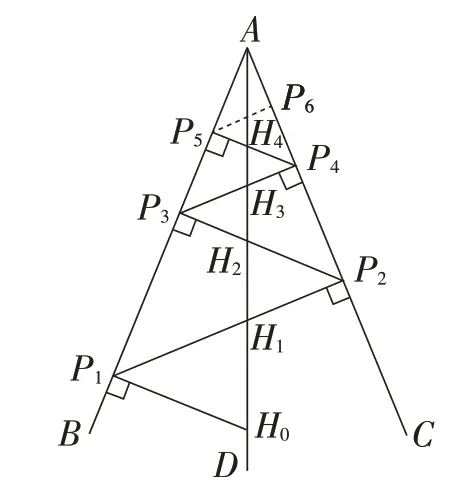
图10

不妨设∠BAC=α，AH0的长为“单位1”.因为H0P1⊥AB，P2P3⊥AB，所以△P2H2H1∽△P1H1H0，两个等腰三角形的相似比又因为AH0平分∠BAC，所以所以k=cosα，H1H0=1-k.由此类推，可得以下结论.

结论1：△PnHnHn-1为等腰三角形，相邻两个等腰三角形的相似比

结论2：Hn+1Hn=H1H0·kn=(1-k)kn.

结论3：HnH0= (1-k)(1+k+k2+…+kn-1)=1-kn，AHn=kn.

题目的第（3）小题相当于当点H2经过AH0的中点时，求α的值.由结论3，可得因为k>0，所以，得α=45°.通过“做减法”，探究问题的本质，用代数方法表达几何图形的性质是如此简洁而美妙！

2.变式推广

聚焦问题的本质，对条件和结论进行普遍化、特殊化、类比、分解和重组等操作，设计变式，进一步推广结论.

变式1：如图11，在等腰三角形ABC中，AB=AC，AD，BE是△ABC的高线，相交于点F，若点F为△ABC的重心，求∠BAC的度数.

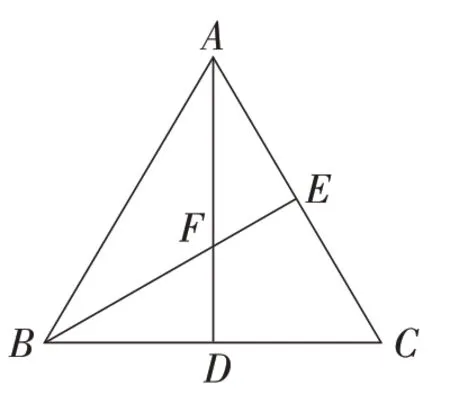
图11

思路：如图12，延长FD至点G，使FD=DG，连接BG.记AG=1，则cos∠BAC=k.易证GB⊥AB，AF=类比图10，点G相当于点H0，点F相当于点H1，由结论3可得所以∠BAC=60°.

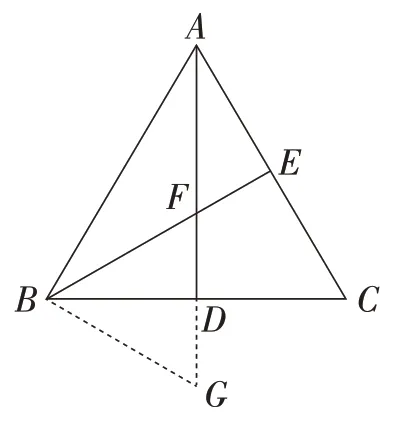
图12

变式2：如图13，在等腰三角形ABC中，AB=AC，AD，BE是△ABC的高线.过点E作EG⊥AB，分别交AB，AD于点G，H；过点G作GI⊥AC，分别交AC，AD于点I，J.若点J为△ABC的外心，求∠BAC的余弦值.

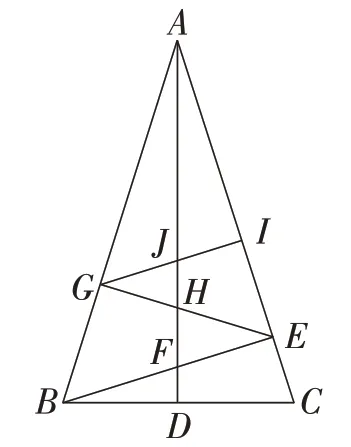
图13

思路：设△ABC外接圆的直径为d，由点J为△ABC的外心，得.类比图10，点J相当于点H3，由结论3可得所以即

变式3：如图14，有一种“特殊的镜子”，无论入射光线如何照射，反射光线与入射光线始终保持夹角为α.现有两面镜子AB，AC，夹角∠BAC=α，有一束光线从∠BAC平分线上的点H0处垂直照射AB，经过4次反射后，经过AH0的四等分点，求α的度数.

思路：变式3中的光线本质上与图10中的高线是一致的，由结论3可得，即所以α=45°.

变式4：如图15，在变式3的基础上，将两面镜子的夹角∠BAC调整为，有一束光线从AC上的点P0处垂直照射AB，经过第n次反射的反射点记为Pn，若，求α的度数.

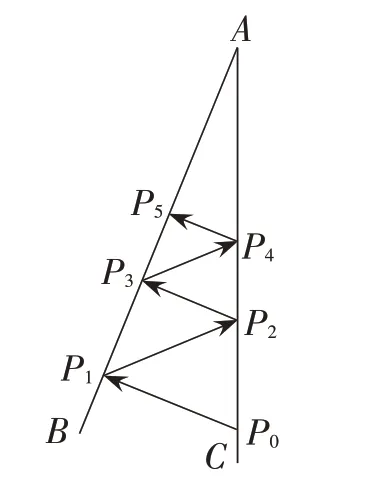
图15

思路：由P0P1∥P2P3∥P4P5，根据平行线分线段成比例定理，可得.如图16，作AB关于AC的对称图形AB′，点P3关于AC的对称点为P3′，可得图16与图10类似.根据结论1，可得所以α=60°.

图16

六、结束语

《义务教育数学课程标准（2022年版）》在“学业水平考试”中明确要求问题的设置要有利于考查对数学概念、性质、关系、规律的理解、表达和应用，注重考查学生的思维过程.2023 年中考数学浙江杭州卷的几何压轴题入口宽，有多种解决问题的路径，使学生均能获得成功的体验，提高考试的信度和效度.问题聚焦对几何图形的基本概念和性质的考查，在几何推理中凸显了思维过程，考查了学生的几何直观和推理能力，在代数推理中考查了学生的抽象能力和运算能力，彰显了“坚持素养立意，凸显育人导向”的命题原则.

怎样解题表的四个步骤和程序组成了一个完善的解题系统.在理解题目的过程中，做“加法”，挖掘隐性条件；在拟订方案过程中，以问题为导向，制订解题策略；在执行方案过程中，添加辅助线，完善解答过程；在回顾反思过程中，去除辅助图形，探寻本质，在变式中运用性质，形成系统性的解题方法，提升学生的数学思维能力和学科素养.正如罗素所说：数学，如果正确地看它，不但拥有真理，而且也具有至高的美.一旦形成系统性的解题方法，找到问题背后的本质和规律后，我们就能体会数学中至高的美.