用数学思想引领问题探究
——以网格中的锐角三角函数题为例
翟丽红
(辽宁省鞍山市第五十一中学)
数学在形成人的理性思维、科学精神和促进个人智力发展中发挥着不可替代的作用.数学思想能引领学生获得解决问题的方法,帮助学生训练逻辑思维,提高解决问题的能力.一方面,初中数学知识的应用依托于数学问题的解决,数学思想方法有助于学生发现问题中的规律和共性;另一方面,在面对数学问题时,不妨尝试从多个角度展开分析,从而探索出数学问题背后的奥秘.这种依托数学思想的探究性学习,既有利于提升学生解决问题的能力,还能促进学生探究精神、创新精神的形成和发展.
求锐角三角函数值是历年中考数学考查的热点.近几年以网格为背景考查锐角三角函数的试题越发受到命题者的青睐.网格中的三角形大多是一般三角形,需要学生灵活添加辅助线构造直角三角形,因此这类试题能有效考查学生的思维能力,尤其是利用转化思想解决问题的能力.本文以网格中的锐角三角函数题为例,通过教学实践,对如何用转化思想引领学生探究问题进行探究.
一、明确教学理论框架
数学思想是指现实世界的空间形式和数量关系反映到人们的意识之中,经过思维活动而产生的结果.由此可见,让学生经历数学活动过程是实现其思维转化的重要前提,这对学生的学习能力乃至综合能力的提升至关重要.所谓转化思想,就是把所要解决的问题转化为另一个较易解决的问题或已经解决的问题.其中,“转化”即新知生长点.利用转化思想探究问题解决方案的过程大致如图1所示.

图1
二、基于转化思想探究和解决问题
笔者从两道例题开始,引导学生经历思考、猜想、探究的问题解决过程,然后通过“举一反三”地解决问题来发展学生的思维,巩固学生利用转化思想探究问题和解决问题的方法.
1.例题及活动设计
例1如图2,网格中每个小正方形的边长均为1,点A,B,O都在格点上,求∠AOB的正弦值.
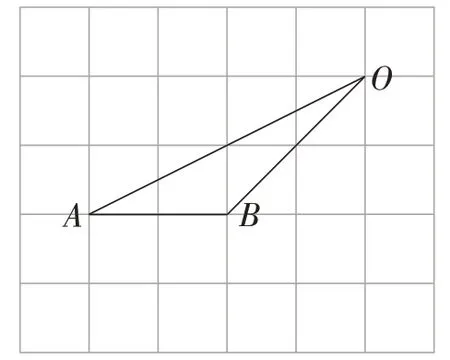
图2
例2如图3,网格中每个小正方形的边长均为1,△ABC的每个顶点都在格点上,求∠BAC的余弦值.

图3
这两道例题初看并不难,但因为∠AOB和∠BAC都不在直角三角形中,所以学生难以直接求出∠AOB的正弦值和∠BAC的余弦值.认真审题后发现,可以利用转化思想解决问题,即借助辅助线构造含有∠AOB或∠BAC的直角三角形.那么,如何引导学生转化呢?基于此,接下来呈现组织学生探究这一类问题解决方法的过程,并对其中蕴含的思想方法进行分析.
为了凸显学生的主体地位和教师的主导作用,笔者让学生在合作学习中交流与分享.在学生合作交流之初,教师有意识地引导学生思考:要求解的问题与哪些已经学过的知识有联系或是相似?学生通过思考发现,此题与直角三角形中的锐角三角函数有联系.这其实就是新知识的生长点,是解决问题的突破口.找到这一生长点,就为探究新知或解法作好了铺垫.
通过合作交流,学生针对例题的求解形成了如下共识.首先,该问题与锐角三角函数有联系,是锐角三角函数的拓展内容;其次,求一个角的三角函数值,除了已经学过的特殊角外,一般锐角的三角函数值求法与其类似,即把锐角置于直角三角形中;最后,添加辅助线构造直角三角形.如果直角顶点恰好在格点上(如例1),那么可以先利用勾股定理求出三角形的边长,然后利用锐角三角函数的概念求解;如果直角顶点不在格点上(如例2),那么可以先根据等积法或勾股定理等方法求出相关边的长度,然后利用锐角三角函数的概念求解.
2.解法探究
对于例1,将∠AOB置于一个直角三角形中有多种辅助线的作法可供选择,如过点B作OA的垂线或过点B作OB的垂线等.但因为这样作辅助线后的垂足不在格点上,所以这两种作辅助线的方案被否定.此时,不妨摆脱在△AOB内部作辅助线的思维定式,将视角扩大至整个网格图.不难发现,可以延长OB到点C,连接AC(如图4).如此一来,易证得∠ACB=90°,且相关线段的长度较容易求出,问题得以解决.

图4
解:如图4,延长OB到点C,连接AC,易得∠ACO=90°.
在Rt△AOC中,
对于例2,将∠BAC置于一个直角三角形中也有多种辅助线的作法可供选择,如过点C作AB的垂线或过点B作AC的垂线.经过分析,发现这两种方法都能够解决问题.
解:如图5,过点C作AB的垂线,垂足为点D,将△ABC补成正方形AEMN.易得△ABC的面积为6.

图5
在△ABC中,因为
在Rt△ACD中,因为AC=2 5,
对于例2,教师可以启发学生思考:除了点C外,能否过△ABC的其他顶点作对边的垂线?接下来,学生可以尝试过点A作FA⊥BC于点F,过点C作CD⊥AB于点D,如图6所示.此时,可以先根据勾股定理计算得到AB=AC=2 5 ,BC=2 2 ,可知△ABC是等腰三角形.则F是BC的中点,且点F在格点上.所以AF=3 2 .然后,利用等面积法求得CD的长,再根据勾股定理得到AD的长,最后计算出∠BAC的余弦值为
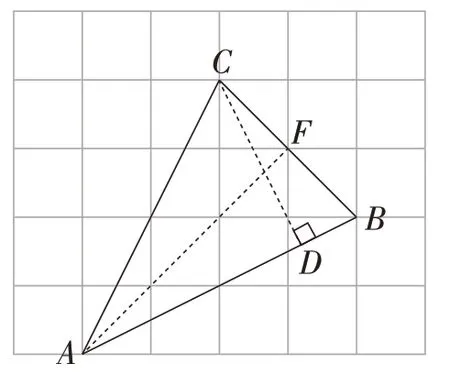
图6
3.举一反三,巩固提升
教师在讲完上述例题后,不妨让学生完成以下练习,以培养学生举一反三的能力,巩固基础知识.
练习:图7 是由边长相同的小正方形组成的网格,A,B,P,Q四点均在格点上,线段AB,PQ相交于点M,则∠QMB的正切值是().

图7
该题既保持了角不在直角三角形中的风格,又独树一帜地采用两条线段相交形成角的方式呈现题目要求,需要学生在掌握解决例题方法的基础上,利用创造性思维寻找解决问题的突破口.首先,仔细观察两条线段及其格点,构造出直角或直角三角形,如图8所示.其次,综合运用勾股定理及逆定理和相似三角形得到相应线段的长,从而解决问题.通过该题,不仅让学生的创造性思维得到了训练,而且让学生在综合运用多个知识点解决问题的基础上,进一步认识到了夯实基础知识和拓展基本技能(包含利用转化思想解决问题)的重要性,有助于发展学生的创新精神.

图8
三、感悟思想
转化思想是初中数学中常见的一种思想方法,它不仅能让复杂的问题变得简单,让生疏的问题变得熟悉,而且能让原本抽象的问题变得直观,让含糊不清之处变得明朗清晰.上述教学过程中,通过作辅助线将原本不在直角三角形中的角转化到直角三角形中,让原本复杂的问题变得简单.因此,笔者认为可以从以下几个方面出发开展转化思想的教学实践,以帮助学生在面对实际问题时能自主利用转化思想解决问题.
首先,要引导学生充分理解问题的条件和所求,帮助学生准确把握问题的本质,找到解题的思路.在数学中,很多问题看似复杂,但只要厘清问题的条件和所求,就能够快速找到解题的方法,从而提升学生分析问题和解决问题的能力,这是发展学生数学核心素养的基础环节.因此,在解决数学问题之前,教师要引导学生仔细阅读和理解问题,明确问题的已知条件和所求,从而使学生选择和应用适当的数学思想方法来解决问题.
其次,教师要指导学生善于将生活问题转化为适当的数学模型.将生活问题转化为数学模型可以帮助学生更好地理解和掌握数学知识,使学生直观地感受数学知识的应用价值,从而加深对知识的理解.同时,可以激发学生对数学学习的兴趣和热情.生活中的问题往往是复杂多样的,将其抽象为数学问题来解决,可以让学生感受到数学的魅力和神奇,从而激发他们对数学的热爱和探索欲.当然,将生活问题转化为数学模型还可以培养学生的创新精神和实践能力.在解决实际问题时,学生需要结合数学知识和实际情况进行分析和思考,提出合理的假设和论证,从而得出有效的解决方案.这不仅能锻炼学生的创造力,还可以帮助学生学会合作与沟通,培养学生的团队精神和实践能力.
最后,要注意细节和思维的连贯性.数学问题通常都有一定的规律性和逻辑性,只有注重细节,才能把握问题的重点和关键点,从而找到解决问题的方法和途径.另外,思维的连贯性是解决数学问题的关键,可以有效避免在解题过程中出现混乱和错误.因此,教师要培养学生认真思考和检验的习惯.
总之,教师既要重视问题解决的过程,更要注重对学生数学思维的培养,这样对学生的发展才更有利.

