中考总复习中知识网络的构建——以“角平分线的画法”微专题为例

陈 兰

（北京市文汇中学）

一、教学缘起

在中考总复习的教学实践中，笔者发现很多学生对于解只包含单一知识点的基础题并不畏惧，但是对于需要综合利用已有知识解决的问题普遍感到困难.这是因为学生对于知识的理解只停留在“只见树木，不见森林”的阶段.在解决综合性问题时，学生不仅要掌握涉及的每个知识点，还要整体把握知识结构并理解知识点间的联系.教师通常让学生以知识板块为单位绘制思维导图，梳理知识脉络，可以按大板块划分为数与代数、图形与几何、统计与概率三部分内容，也可以按小板块划分为方程、不等式、函数、直线形图形、圆等内容.为了帮助学生自主构建知识网络，教师可以以微专题的形式带领学生梳理知识.例如，设置画角平分线，证明两条线段相等，证明两条线段垂直或平行，证明线段或角的和、差、倍、比关系等微专题.这个梳理过程不是机械地照搬教材目录，而是将与之相关的知识点组织成知识网络，帮助学生将知识连点成线、连线成网，最终形成完整且灵活的知识网络.

下面以“角平分线的画法”微专题为例，帮助学生构建相关的知识网络.

如何画一个角的平分线呢？人教版《义务教育教科书·数学》（以下统称“教材”）八年级上册“12.3 角的平分线的性质”中以一个平分角的仪器为引例，讲授了角平分线的一种经典尺规作图方法.教材这样安排的目的既是对全等三角形性质和判定的应用，也是启发学生思考角平分线的尺规作图方法.但是，学习完初中平面几何的全部内容后，在中考总复习阶段，重新回答这一问题时，学生会有怎样的认识呢？笔者尝试在九年级设计“角平分线的画法”这样一节微专题活动课.课前，教师提出如下问题：不限工具，尝试用尽可能多的方法画一个已知角的平分线.课堂上，学生提出了多种作图方法，然后教师引导学生梳理每种作图方法的依据，以及各种方法之间的联系，进而使学生认识各种方法背后的数学本质.

二、方法展示

本节课上，学生给出了如下作图方法.

方法1：如图1，分别在OA，OB上截取OD=OC，连接CD，过点O作OE⊥CD于点E，则射线OE即为所求.

图1

由等腰三角形“三线合一”的性质，可得∠DOE=∠COE.

方法2：如图2，利用任意矩形纸片（或直尺），将矩形一边分别与角的两边对齐，沿矩形的对边画直线a和直线b，两线交于点C，则射线OC即为所求.

图2

这里利用了平行线间的距离处处相等和角平分线的判定定理，转化为作图过程，即将角的两边OA，OB分别平移相同的距离至直线a和直线b处.

方法3：如图3，用圆规分别在OA，OB上截取OD=OC，分别以点C，D为圆心，大于长为半径画弧，两弧交于点E，则射线OE即为所求.

图3

先判定△ODE≌△OCE，由全等三角形的性质得∠DOE=∠COE.这个方法就是角平分仪的设计原理.

方法4：如图4，分别在OA，OB上截取OD=OC，OG=OF，连接CG，DF，交于点E，则射线OE即为所求.

图4

先判定△OCG≌△ODF，再判定△DEG≌△CEF，进而判定△DEO≌△CEO，由全等三角形的性质得∠DOE=∠COE.

方法5：如图5，分别在OA，OB上截取OD=OC，将直角三角板的直角顶点置于点D处，使一条直角边与DA重合，沿另一条直角边画直线DG交OB于点G，同样作直线CF⊥OB交OA于点F，CF与DG交于点E，则射线OE即为所求.

图5

这里先判定Rt△DEO≌Rt△CEO，由全等三角形的性质得∠DOE=∠COE.

方法6：如图6，分别在OA，OB上截取OD=OC，分别以点C，D为圆心，以OC长为半径画弧，两弧交于点E，则射线OE即为所求.

图6

由四边相等的四边形是菱形，以及菱形的对角线平分一组对角的性质得证.

方法7：如图7，将圆形纸片（圆心E打孔）放在∠AOB的内部，使圆和角的两边相切，则射线OE即为所求.

图7

由切线长定理“过圆外一点的两条切线长相等”及三角形全等得证.

方法8：如图8，将圆形纸片（圆心O打孔）的圆心与角的顶点重合，角两边与圆交于点C，D，对折圆形纸片使点C与点D重合，由垂径定理推得折痕为直径所在直线，此时∠DOE=∠COE=∠DFC，则射线OE即为所求.

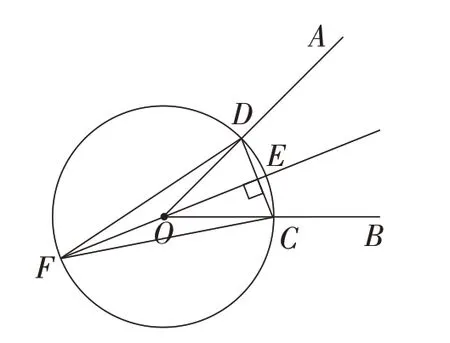
图8

方法9：如图9，将小圆纸片的圆心O与角的顶点重合，小圆纸片与角的两边交于点C和点D，使点C和点D同时在大圆O′上，则两圆心的连线OO′即为所求.

图9

方法10：如图10，在OA上任取一点D，过点D作DF∥OB，以点D为圆心，DO长为半径画弧，与DF交于点E，则射线OE即为所求.

图10

这里用到了平行线的性质和等腰三角形的性质，将角等量转移，得∠DOE=∠DEO=∠EOB.

方法11：如图11，在OA上任取一点D，在OB上截取OC=3OD，连接CD，取线段CD靠近点D的四等分点为E，则射线OE即为所求.

图11

此法可由面积法得证.如图12，过点E向角两边作垂线，分别交OA，OB于点H，I，则又因为，所以EH=EI.所以OE为∠AOB的平分线.

图12

或者由平行线分线段成比例定理的逆命题可证.如图13，过点D作DG∥OC，交OE于点G，得又因为，所以，进而得DG=OD.所以∠DGO=∠DOG=∠GOB.此法还可以推广至一般情况，截取OC=nOD，在CD上截取n+1等分点.

图13

三、总结归纳

学生展示各种作图方法后，教师通过以下问题引导学生构建知识网络.

问题1：这些方法的本质是什么？试用一句话简要概括每种方法.

学生总结如下.

方法1 借助了等腰三角形的轴对称性；方法2～方法5构造了轴对称变换下的两个全等三角形；方法6构造了菱形，借助菱形的性质来判断；方法7 利用了圆的轴对称性，以及圆和角两边相切的特殊的轴对称位置关系；方法8利用了同弧所对圆心角和圆周角间的二倍关系，及圆的轴对称应用——垂径定理；方法9借助了两圆相交时圆心的连线是其对称轴的特点；方法10利用“等腰+平行线”构造出角平分线；方法11可以由方法10的思路延伸得到.如果将平行条件换作等价条件呢？因而想到尝试用线段成比例推导平行的方法.

问题2：方法之间有何联系？

方法1和方法8的本质相同，圆的垂径定理也源于圆与等腰三角形共轴，它们都是轴对称性的体现；方法2和方法7同源，将方法7的操作方法转化为作图方法则满足方法2 的条件，切线长定理本质上是圆的轴对称性的体现；方法3 和方法6 都是构造翻折形全等（筝形或菱形），方法3 更具有一般性；方法4和方法5都是构造“燕尾形”全等，且方法5具有特殊性.

问题3：哪些方法有共性，可以归为一类？

经过再提炼，学生发现方法1～ 9 都抓住了角是轴对称图形的本质，构造另一个轴对称图形使之与角共轴，因此找到角的对称轴即角平分线所在直线.这些方法几乎涵盖了我们学过的等腰三角形、轴对称变换下的两个全等三角形、菱形和圆这些轴对称图形.再观察图形，学生发现角及角平分线的图形被“包含”在这些具有轴对称性的基本图形中.这是因为角是更简单的轴对称图形，可以被组合在更复杂的轴对称图形中.学生体会到：研究图形的性质要抓住对称性，进而从这个宏观的本质属性中发现图形元素的数量关系和位置关系这些微观表现.例如，圆的垂径定理、切线长定理是其轴对称性的表现，平行四边形的性质是由其中心对称性统领.那么，如何“放置”这个构造的轴对称图形才能使之与角共轴呢？学生进一步归纳出使角和这个轴对称图形至少有一对公共的对称点.教师追问：怎么借助正多边形或者抛物线画角平分线？其道理与前面是相通的，学生可以自行探究.至此，学生抓住了画角平分线的本质.

四、教学反思

《义务教育数学课程标准（2022年版）》指出，在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系.通过合适的主题整合教学内容，帮助学生学会用整体的、联系的、发展的眼光看问题，形成科学的思维习惯，发展数学核心素养.中考复习课正是落实这一教学目标、践行新课程理念的有效载体.

什么内容和形式的复习课能有效凸显其定位和价值？复习课的教育价值是建立系统和简约的知识体系，引导学生提炼数学思想和方法，积累数学活动经验，并把获得的数学知识、思想方法和活动经验迁移应用，在此过程中发展学生的数学核心素养.微专题形式的复习课正是帮助学生在知识的结果性认知基础上，根据当前的学习活动去联想、调动、激活以往的知识经验，以融会贯通的方式对内容进行组织，使相关单元知识之间建立起具有简约性、多触点、结构化的网络.

什么教学形式的复习课能更好地调动学生思维的积极性，让学生有更多收获？在强调活动与体验的实践活动课中，学生能真正成为学习的主体，在实践、探究、体验、反思、合作、交流等学习过程中深化认识、感悟基本思想、积累基本活动经验.学生亲身经历知识网络的形成、发展、联结过程，将静态的知识点激活，全身心地体验知识间的联结，这样才能自主构建属于自己的灵活的知识网络.