运动学误差模型变体下的机械臂标定精度研究

蒋周翔，苏瑞，秦鹏举，蒙月晨，龙忠杰，宋宝，唐小琦

(1.北京信息科技大学机电工程学院，北京 100192；2.华中科技大学机械科学与工程学院，湖北武汉 430074)

0 前言

机械臂末端绝对定位精度是评价机械臂技术水平的重要指标，决定了机械臂能否准确完成各种作业任务。运动学标定是在机械臂硬件结构确定后，从软件角度出发的保证机械臂绝对定位精度的有效方式。运动学误差建模是运动学标定的第一个环节，因此模型完整、连续、最小、精确以及良态是最终标定结果有效的先决条件[1]。

运动学误差模型具有代表性的研究成果有DENAVIT和HARTENBERG共同提出的机械臂建模准则SD-H(Standard Denavit-Hartenberg)[2]。 HAYATI、MIRMIRANI[3]为解决相邻平行关节标定时参数不连续问题，在SD-H基础上增加了一个绕Y轴旋转的角度。CRAIG[4]提出一种区别于SD-H的建模方法，即MD-H(Modified Denavit-Hartenberg)，该方法将连杆坐标系由连杆末端移到前端。这种建模方法除串联机构外，也适用于树状或闭环机构。KHALIL、DOMBRE[5]在此基础上借鉴HAYATI等的思路，为MD-H模型的相邻平行关节也加入了一个绕Y轴的旋转角度，使之同样在标定时满足模型连续性。STONE[6]提出一种六参数的S-model，旨在提高机械臂建模的完整性。近些年，还有部分学者提出了基于POE(Product of Exponentials)[7]的标定模型，同时符合了模型的完整性、连续性以及最小性。

上述模型绝大多数满足了完整、连续和最小的要求，但业界最广泛采用的仍然是基于Hayati参数的SD-H和MD-H运动学误差模型。除上述3种特性外，目前还有部分学者针对这两种模型的运动学误差辨识精度进行了相关研究，通常是在选定建模规则后，从测量环节寻求改进方案，比如优化测量构型[8]或改良测量装置[9-10]。前者能够提高模型的观测指数，进而使运动学误差在末端位姿误差上产生更明显的倍增效果，以减小测量噪声干扰；后者有助于测量仪器获得更高维度的末端位姿误差信息，提高运动学参数误差的可辨识性。

除测量构型和测量装置外，运动学误差的建模方式也对标定精度有显著影响，然而目前还未见到相关研究的公开报道。具体而言，SD-H和MD-H运动学误差建模时遵循的旋转变换顺序不同，将使模型性态水平产生明显差异。此外，这两种建模规则均基于微小误差假设从真实正运动学模型中独立出运动学参数误差，以此建立误差参数到关节位姿误差的映射关系，进而最终得到线性的机械臂运动学误差模型，由此可知建模阶段引入了线性化误差。模型性态水平与线性化误差均会影响误差辨识结果的准确性，所以有必要对各类SD-H和MD-H运动学误差模型的性态水平与线性化误差进行量化分析和对比，以此选择辨识精度最高的建模方法。

面对上述现状，本文作者以建模环节为切入点，以不同欧拉变换顺序下的SD-H和MD-H运动学误差模型为对象，通过研究各模型的性态水平和线性化误差，以及对比分析各模型在较高测量噪声干扰下的运动学参数误差辨识精度，综合验证了性态水平和线性化误差对标定精度的影响程度，进而为机械臂运动学误差模型的建立方式和各类型参数的标定方法提供了理论依据。

1 不同欧拉变换的SD-H运动学误差模型

1.1 SD-H模型中的坐标系与参数设置

对于一台6R串联型机械臂，依据SD-H方法建立的各关节坐标系如图1所示。

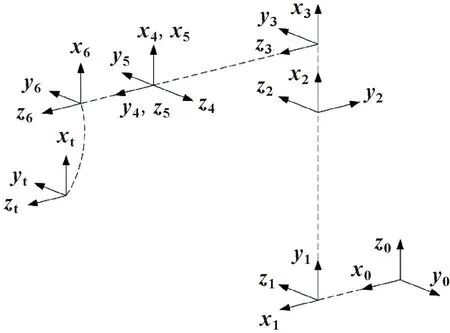
图1 SD-H模型下的机械臂关节坐标分布

其中，如前文所述，由于第2、3关节轴线接近平行，使得传统SD-H模型在标定三关节参数时所得辨识结果不连续，因此通常引入β2来替代d2，如图2所示。

图2 SD-H模型下的相邻平行关节坐标系变换

由图2可知，构造一个过坐标系2原点o2且垂直于z1轴的平面，其与z1交点为坐标系1的原点o1。先将x1绕z1旋转θ2，使其与o1o2方向重合。再将坐标系2沿该方向平移a2，使o1与o2重合。最后分别绕此时的x1轴和y2轴旋转α2和β2，使此时的z1轴与z2轴重合，完成坐标系1到坐标系2的转换。

此处，由于旋转α2和β2的目的仅为使z1轴与z2轴重合，因此旋转顺序可以交换。又因为SD-H建模要遵循先绕z轴再绕x轴旋转的规则，所以3个角度旋转顺序可排列为θ2→α2→β2或θ2→β2→α2，进而得到两种不同欧拉变换下的SD-H运动学误差模型。

1.2 z-x-y欧拉变换的SD-H运动学误差模型

对于相邻垂直关节，即i≠2时，坐标系i-1到坐标系i的齐次变换为

i-1Ti=Rz(θi)Dz(di)Dx(ai)Rx(αi)

(1)

在z-x-y欧拉变换下，对于相邻平行关节，即i=2时，坐标系i-1到坐标系i的齐次变换为

i-1Ti=Rx(αi)Dx(ai)Rz(θi)Ry(βi)

(2)

当i≠2时，令Δui=[δθi，δdi，δai，δαi]表征运动学参数误差向量，则该向量的转置到关节坐标系i位姿误差的映射矩阵为

(3)

当i=2时，令Δui=[δθi,δai,δαi,δβi]表征运动学参数误差向量，则该向量的转置到关节坐标系i位姿误差的映射矩阵为

(4)

令Δu=[Δu1,Δu2,…,Δu6]T，则在第j个测量构型处，所有参数误差造成的末端执行器坐标系t的位姿误差为

Ej=JjΔu

(5)

其中：

(6)

且

(7)

其矩阵元素来源于

(8)

其中：

6Tt=Dx(xt)Dy(yt)Dz(zt)Rx(αt)Ry(βt)Rz(γt)

(9)

如果有m个测量构型，则可建立运动学误差模型

E=JΔu

(10)

其中

(11)

1.3 z-y-x欧拉变换的SD-H运动学误差模型

在z-y-x欧拉变换下，对于相邻平行关节，即i=2时，坐标系i-1到坐标系i的齐次变换为

i-1Ti=Rz(θi)Dx(ai)Ry(βi)Rx(αi)

(12)

当i≠2时，Δui的转置到关节坐标系i位姿误差的映射矩阵与式(3)相同。当i=2时，Δui的转置到关节坐标系i位姿误差的映射矩阵为

(13)

在此基础上，采用与式(5)—(11)相同的方法即可得到z-y-x欧拉变换下的SD-H运动学误差模型。

2 不同欧拉变换的MD-H运动学误差模型

2.1 MD-H模型中的坐标系与参数设置

对于一台6R串联型机械臂，依据MD-H方法建立的各关节坐标系如图3所示。

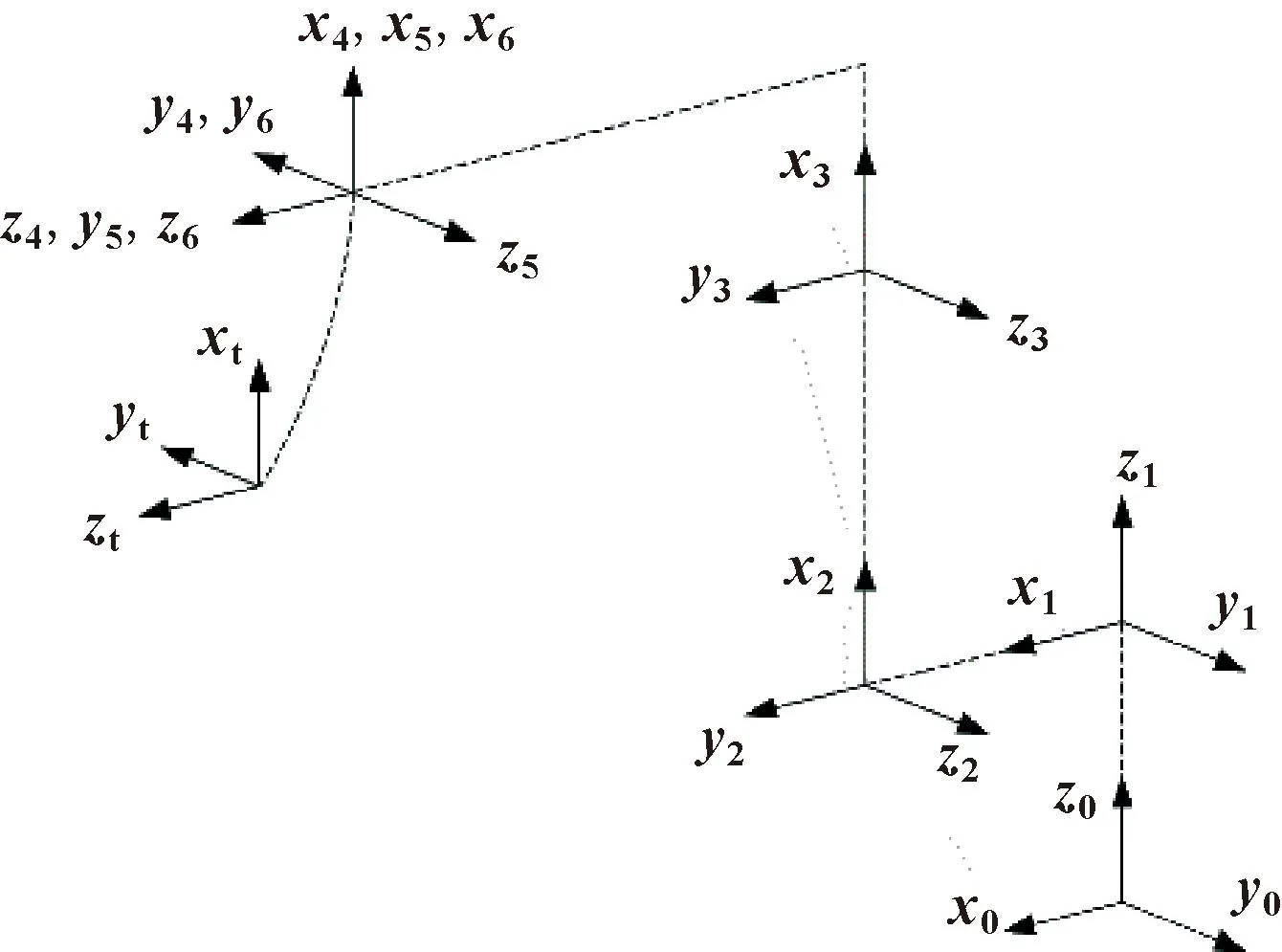
图3 MD-H模型下的机械臂关节坐标分布

如前文所述，由于第2、3关节轴线接近平行，使传统MD-H模型在标定三关节参数时所得辨识结果不连续，因此引入β3来替代d3，如图4所示。

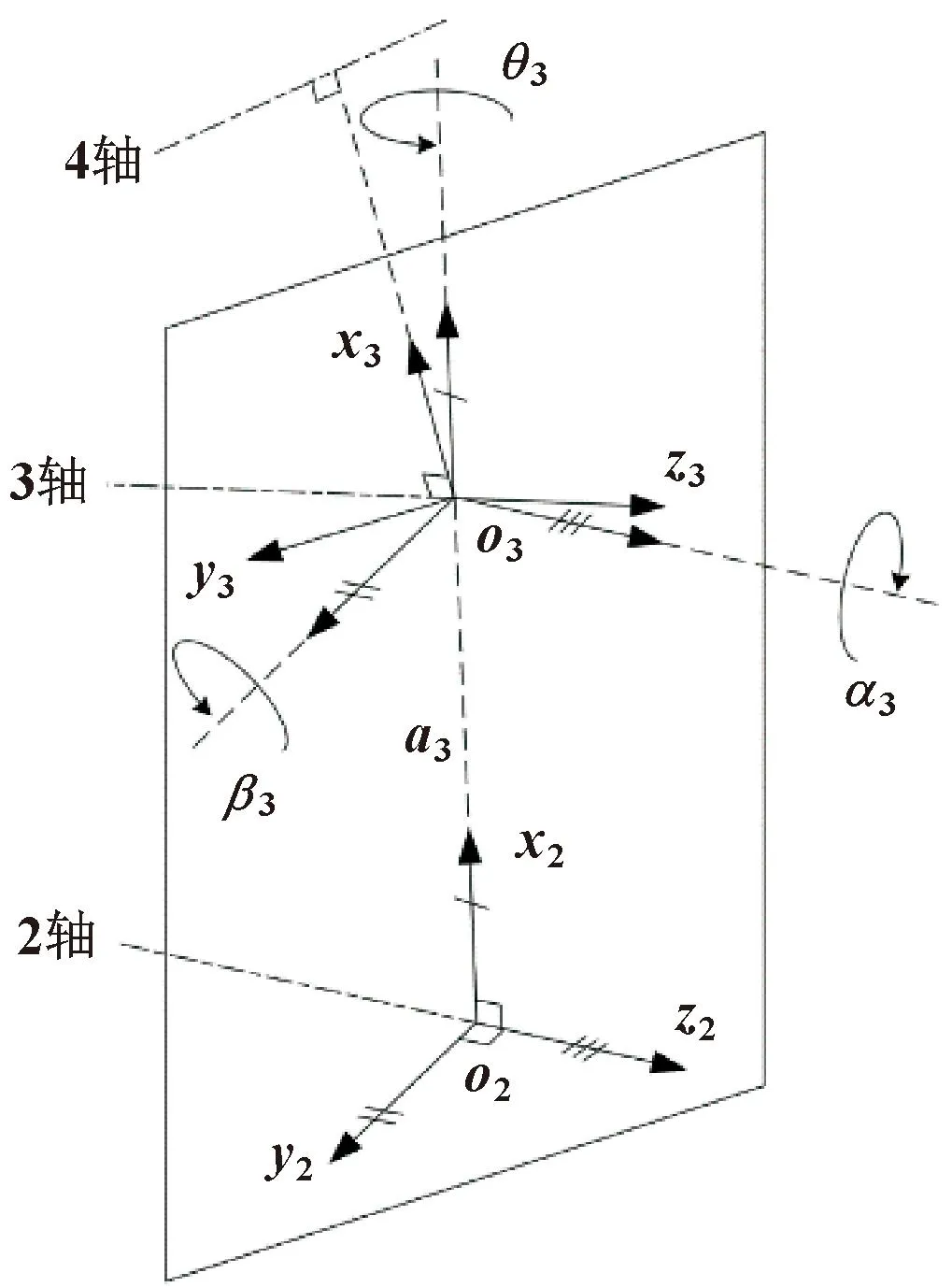
图4 MD-H模型下的相邻平行关节坐标系变换

由图4可知，构造一个过坐标系3原点o3且垂直于z2轴的平面，其与z2交点为坐标系2的原点o2。先将坐标系2沿o2o3方向平移a3，使o2与o3重合。然后分别绕此时的x2、y2和z2轴旋转α3、β3和θ3，使x2、y2和z2轴分别与x3、y3和z3轴重合，完成坐标系2到坐标系3的转换。

此处，由于旋转α3、β3和θ3仅为使坐标系2与坐标系3重合，因此3个旋转的顺序可以交换。又因为要遵循先绕x轴再绕z轴旋转的规则，所以3个角度的旋转顺序可排列为β3→α3→θ3、α3→β3→θ3和α3→θ3→β3，进而得到3种不同欧拉变换下的MD-H运动学误差模型建模方式。

2.2 y-x-z欧拉变换的MD-H运动学误差模型

对于相邻垂直关节，即i≠3时，坐标系i-1到坐标系i的齐次变换为

i-1Ti=Rx(αi)Dx(ai)Rz(θi)Dz(di)

(14)

在y-x-z欧拉变换下，对于相邻平行关节，即i=3时，坐标系i-1到坐标系i的齐次变换为

i-1Ti=Dx(ai)Rx(βi)Rx(αi)Rz(θi)

(15)

当i≠3时，Δui=[δθi，δdi，δai，δαi]的转置到关节坐标系i位姿误差的映射矩阵为

(16)

当i=3时，Δui=[δθi,δai,δαi,δβi]的转置到关节坐标系i位姿误差的映射矩阵为

(17)

在此基础上，采用与式(5)—(11)相同方法即可得到y-x-z欧拉变换下的MD-H运动学误差模型。

2.3 x-y-z欧拉变换的MD-H运动学误差模型

在x-y-z欧拉变换下，对于相邻平行关节，即i=3时，坐标系i-1到坐标系i的齐次变换为

i-1Ti=Dx(ai)Rx(αi)Rx(βi)Rz(θi)

(18)

当i≠3时，Δui的转置到关节坐标系i位姿误差的映射矩阵与式(16)相同。当i=3时，Δui的转置到关节坐标系i位姿误差的映射矩阵为

(19)

在此基础上，采用与式(5)—(11)相同的方法即可得到x-y-z欧拉变换下的MD-H运动学误差模型。

2.4 x-z-y欧拉变换的MD-H运动学误差模型

在x-z-y欧拉变换下，对于相邻平行关节，即i=3时，i-1坐标系到i坐标系的齐次变换为

i-1Ti=Dx(ai)Rx(αi)Rz(θi)Rx(βi)

(20)

当i≠3时，Δui的转置到关节坐标系位姿误差的映射矩阵与式(16)相同。当i=3时，Δui的转置到关节坐标系i位姿误差的映射矩阵为

(21)

在此基础上，采用与式(5)—(11)相同的方法即可得到x-z-y欧拉变换下的MD-H运动学误差模型。

3 各误差模型的性态水平仿真分析

3.1 SD-H运动学误差模型性态水平

所有仿真均以BORUNTE的BRTIRUS1510A型机械臂为对象。在SD-H建模规则下，该机械臂D-H参数名义值如表1所示。

表1 机械臂SD-H参数赋值

其第6关节到末端执行器坐标系t的变换参数如表2所示。

表2 SD-H规则下的第6关节到坐标系t变换矩阵赋值

在此基础上，采用DETMAX算法[11]生成24个测量构型，即可依据第1.2节和1.3节所述方法分别建立运动学误差模型。

运动学误差模型的性态水平是Δu辨识精度的决定因素之一，可通过式(10)中的J矩阵的观测指数[12-13]、条件数以及是否满秩对其性态水平进行分析。观测指数O1和条件数C计算公式分别为

(22)

(23)

其中：σ1～σ24是J的奇异值并且σ1≥σ2≥ … ≥σ24；m为测量构型的个数。

据此，z-x-y和z-y-x这两种欧拉变换下的SD-H运动学误差模型性态水平如表3所示。

表3 SD-H运动学误差模型性态水平

由表3可知：在两种欧拉变换下，SD-H运动学误差模型的J矩阵均为满秩，且观测指数和条件数均非常接近，因此具有接近的性态水平。

3.2 MD-H运动学误差模型性态水平

在MD-H建模规则下，BRTIRUS1510A机械臂D-H参数名义值如表4所示。

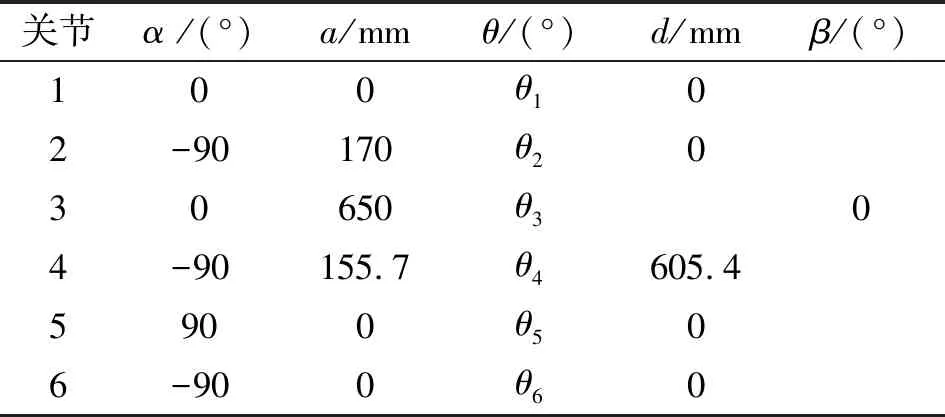
表4 机械臂MD-H参数赋值

其第6关节到末端执行器坐标系t的变换参数如表5所示。

表5 MD-H规则下的第6关节到坐标系t变换矩阵赋值

同样采用DETMAX算法生成24个测量构型，即可依据第2.2—2.4节所述方法分别建立运动学误差模型，并由式(22)(23)求出观测指数和条件数，如表6所示。

表6 MD-H运动学误差模型性态水平

由表6可知：在y-x-z和x-y-z这两种欧拉变换下，MD-H运动学误差模型的J矩阵均为满秩，且观测指数和条件数均非常接近，因此具有接近的性态水平；然而在x-z-y欧拉变换下，J并不满秩，由此导致观测指数较小且条件数极大，此时的运动学误差模型为严重病态，无法准确识别24个运动学参数误差，因此不推荐采用x-z-y欧拉变换下的MD-H运动学误差模型用于标定。

综合表3、6可知：MD-H模型相比SD-H模型具有更高的观测指数和更小的条件数，即更良好的性态水平，但仅凭这一结果还难以对两类模型的标定精度做出准确评价，而需结合模型线性化误差的影响进行综合分析。

4 各误差模型的线性化误差仿真分析

4.1 线性化误差计算流程

首先假定各项运动学参数误差值如表7所示。

接着针对每种欧拉变换，采用式(5)—(11)建立其运动学误差模型，进而得到m个测量构型处的坐标系t位姿误差E，提取E在xt、yt、zt方向的位置误差，得到3m×1维的位置误差向量ΔpJ。

然后基于同样的m个测量构型，结合名义正运动学模型(式(1)(2)(12)(14)(15)(18)(20))及其真实正运动学模型(将式(1)(2)(12)(14)(15)(18)(20)中的θi、di、ai、αi和βi分别替换为θi+δθi、di+δdi、ai+δai、αi+δαi和βi+δβi)，可得到每个测量构型下对应的坐标系t位姿误差ET。提取ET在xt、yt、zt方向的位置误差，得到3m×1维的位置误差向量ΔpT。

最后，由于ΔpT来源于无线性化误差的正运动学模型，因此将ΔpJ与ΔpT按下式相减，即可得到各种运动学误差模型的线性化误差大小。

(24)

4.2 SD-H运动学误差模型的线性化误差

依据第4.1节所述方法及表7误差值，得到z-x-y和z-y-x变换下的SD-H运动学误差模型线性化误差，分别如图5、6所示。

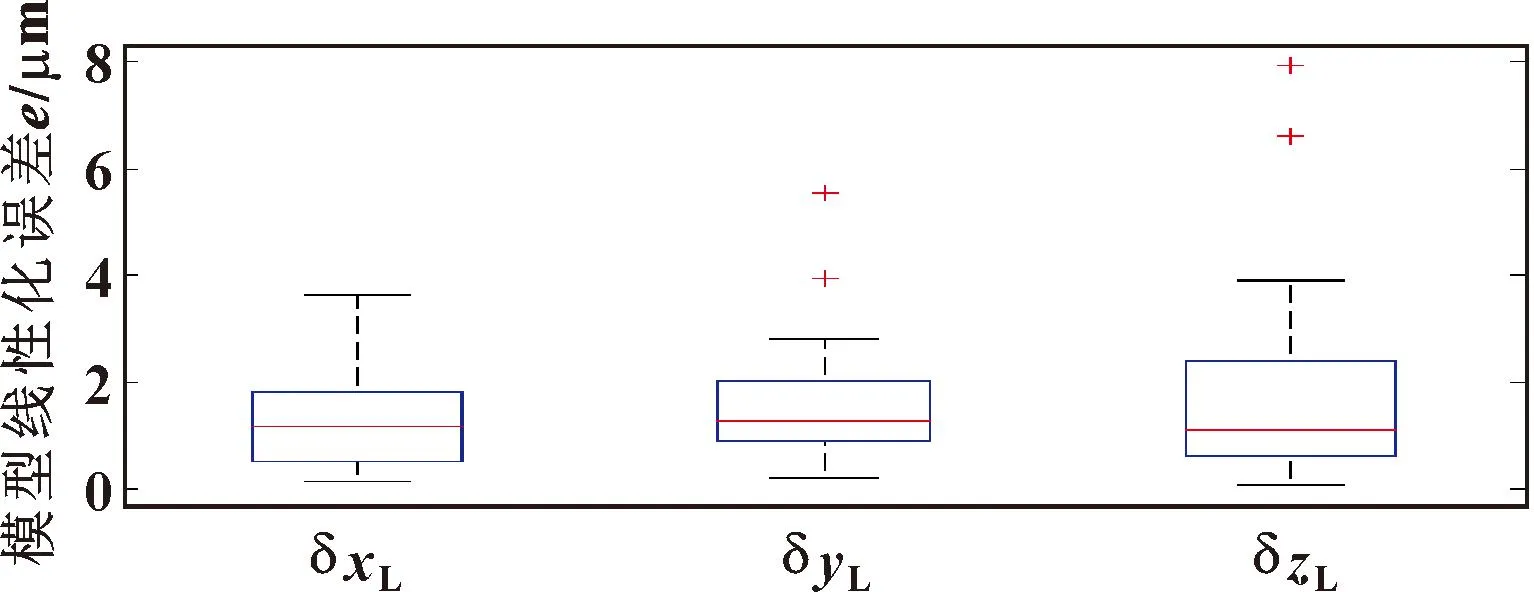
图6 z-y-x变换下的SD-H运动学误差模型线性化误差

由图5、6可知：两种SD-H运动学误差模型线性化误差均为微米级。通常，机械臂末端绝对定位精度在未标定前为毫米级。因此可以初步预测，微米级线性化误差对Δu辨识结果的影响可以忽略不计。

4.3 MD-H运动学误差模型的线性化误差

按照第4.1节所述方法，得到y-x-z和x-y-z变换下的MD-H运动学误差模型线性化误差(x-z-y型不推荐使用，因此不参与仿真验证)，分别如图7、8所示。

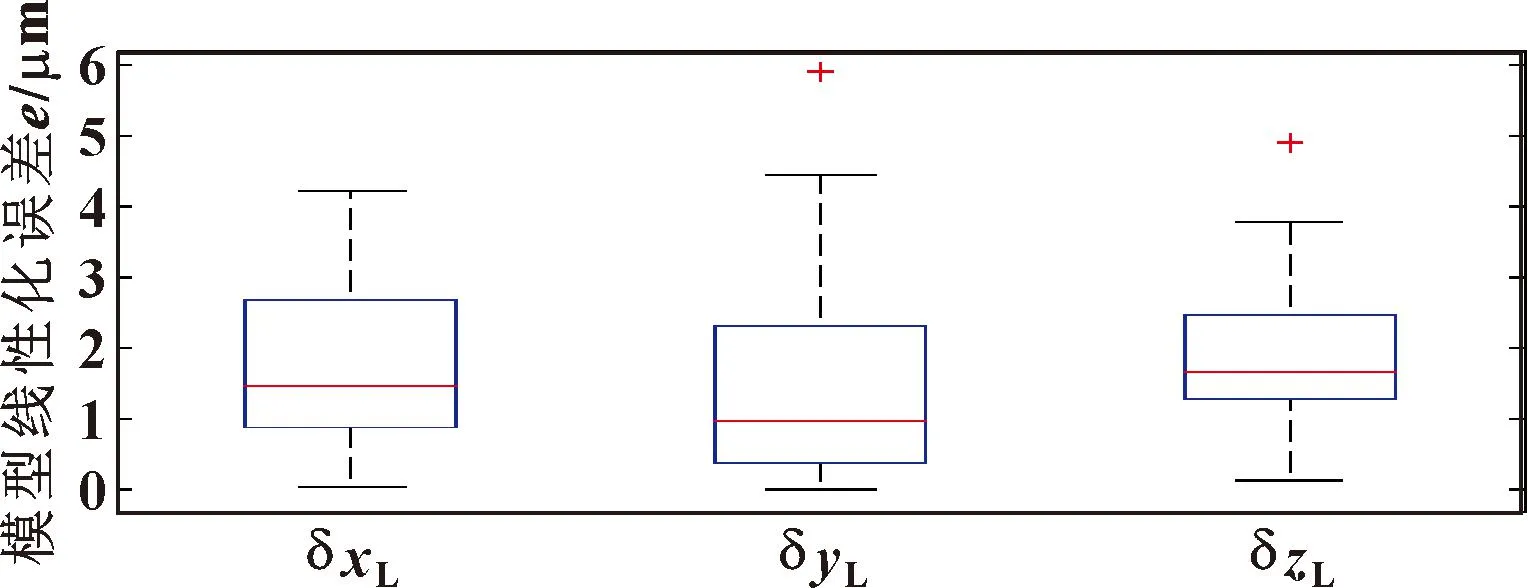
图7 y-x-z变换下的MD-H运动学误差模型线性化误差

图8 x-y-z变换下的MD-H运动学误差模型线性化误差

由图7、8可知：MD-H误差模型线性化误差与SD-H为同一量级。虽然前文所述MD-H误差模型的性态水平优于SD-H，但二者对Δu的辨识精度还需在后续仿真中进一步验证。

5 运动学参数辨识精度仿真验证

5.1 仿真流程

仿真的目的是验证第3小节所述4种运动学误差模型在模拟的真实场景下对Δu的辨识精度。首先是模拟测量过程中的随机误差。假定采用一般精度水平的视觉测量方式，设视觉测距精度为±1 mm且机械臂末端靶标尺寸为80 mm×80 mm，测量不确定度可参考表8设定。

表8 测量不确定度赋值

然后依次以4种运动学误差模型为对象，按照表8所示分布，为位姿误差向量E随机生成104组测量不确定度ΔE，用E+ΔE替代式(10)中的E，即可按下式求解出Δu的实际辨识结果Δua

ΔE+E=JΔua

(25)

其中：E+ΔE和Δua分别为120×104维和24×104维矩阵。对Δua每行求平均值，再按下式计算出Δu向量中第k个运动学参数误差的辨识误差占比

(26)

其中：Δu(k)的数值与表7一致。分别对每种运动学误差模型执行上述仿真流程102次，求各δu(k)对应的102个数据的均值作为其辨识误差。

5.2 辨识结果及分析

两种SD-H运动学误差模型的δu(k)分别如图9、10所示。

图9 z-x-y变换下的SD-H模型对Δu的辨识精度

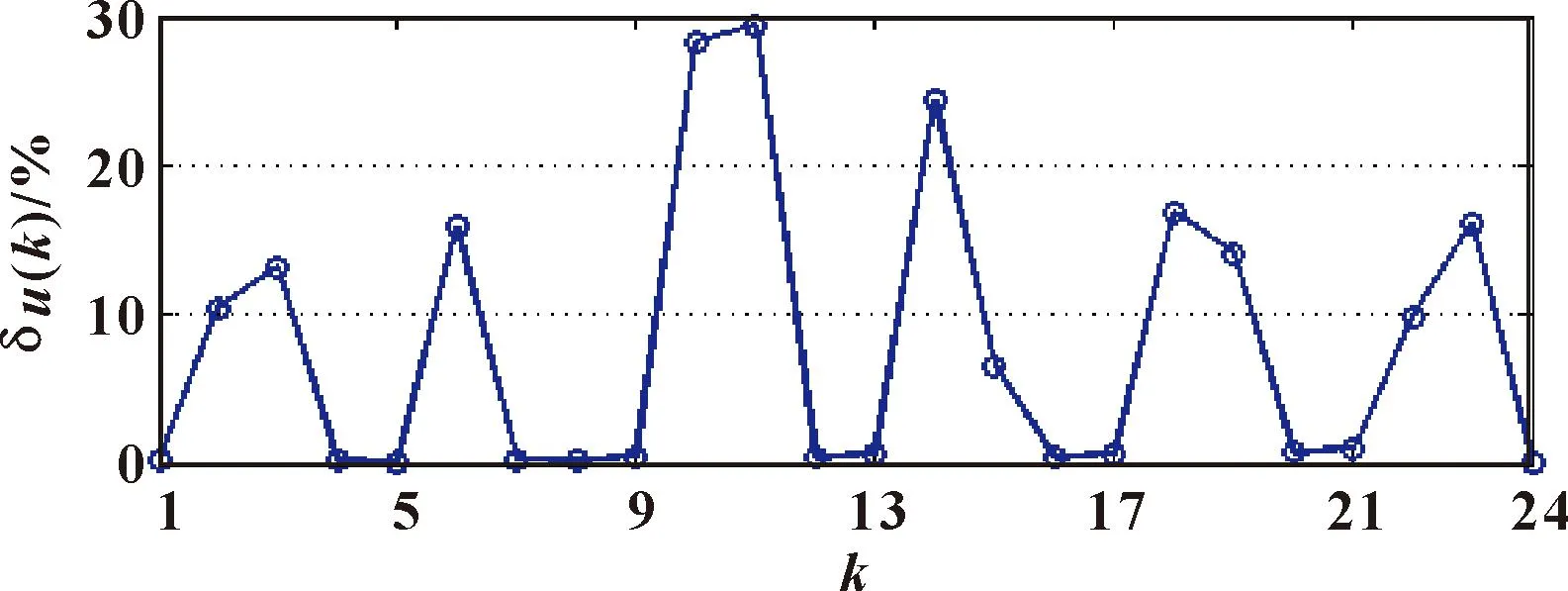
图10 z-y-x变换下的SD-H模型对Δu的辨识精度

由图9、10可知：两种SD-H运动学误差模型均对角度类Δu(δθi、δαi和δβi，对应图中k=1，4，5，7，8，9，12，13，16，17，20，21，24)具有极高辨识精度(0.1%～1.1%)，而对位置类Δu(δdi和δai，对应图中k=2，3，6，10，11，14，15，18，19，22，23)的辨识精度明显降低(6.6%～39.3%)。

两种MD-H运动学误差模型的δu(k)分别如图11、12所示。

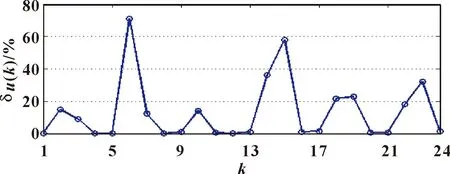
图11 x-y-z变换下的MD-H模型对Δu的辨识精度

图12 y-x-z变换下的MD-H模型对Δu的辨识精度

由图11、12可知：两种MD-H运动学误差模型均对角度类Δu(δθi、δαi和δβi，对应图中k=1，4，5，8，9，11，12，13，16，17，20，21，24)具有较高辨识精度(0.1%～1.6%)，而对位置类Δu(δdi和δai，对应图中k=2，3，6，7，10，14，15，18，19，22，23)辨识精度较差(4.7%～71.2%)。与SD-H相比，MD-H对距离类Δu的辨识精度有所降低。

5.3 仿真结论

由仿真数据可初步得出结论：

(1)x-z-y变换下的MD-H运动学误差模型不满秩，存在冗余的待辨识参数，因此不适用于标定。

(2)虽然MD-H比SD-H运动学误差模型具有更高的性态水平，引入的线性化误差量级等同，但在两类因素综合影响下，SD-H模型却具有更高的运动学参数误差辨识精度。因此推荐采用SD-H模型标定串联机械臂。

(3) SD-H和MD-H运动学误差模型均对角度类Δu具有较高辨识精度，而对距离类Δu辨识精度较低，原因是距离类Δu在模型中不产生倍增效应。因此当测量噪声量级与距离类Δu接近甚至更大时，其辨识精度将急剧劣化。因此若对标定效率无特殊要求，可采用无模型辨识方法如CPA(Circle Point Analysis[14-15])来解算距离类Δu。

6 结束语

本文作者首先依据不同的欧拉变换顺序分别建立了基于SD-H和MD-H规则的运动学误差模型；然后量化分析了以上5种运动学误差模型的性态水平以及其中4种满秩模型的线性化误差；最后对4种满秩模型的运动学参数误差辨识精度进行了对比分析，以此综合评价模型性态水平和线性化误差对标定结果的影响程度，为机械臂高精度标定模型的建立以及各类误差辨识方法的合理实施提供了理论依据和参考。

下一步研究计划是从理论推导上继续挖掘MD-H运动学误差模型存在冗余参数且线性化误差偏大的根本原因，并据此探索针对标定方法的优化方案。在此基础上搭建试验平台对4种模型在真实场景下的标定精度进行对比，并验证优化方案的可行性。