架空裸导线涂覆机器人作业关键因素分析及其参数优化

陈水胜，杨博 ，蔡志国，陈俊，王君

(1.湖北工业大学机械工程学院，湖北武汉430068；2.武汉华仪智能设备有限公司，湖北武汉430100)

0 前言

架空线路作为配电网的主要组成部分，是我国电力传输的主要形式。架空线路覆盖广阔，输电距离长。其安全稳定运行与配电网的安全可靠息息相关[1]。市区配电网线路往往穿越人口密集区域，市郊、山区等地区的架空裸导线经常会跨越池塘、植被及村落等区域。因为裸导线及破损导线直接或间接造成的人员伤亡、森林火灾等事故时有发生。传统的绝缘处理方法为在停电情况下，人工悬挂在电线杆上直接更换绝缘电缆[2-3]或进行绝缘护套包覆处理[4]。这种采用人工的方式效率极低，而且作业人员安全性得不到保障。因此，研发先进的裸导线绝缘化技术及装备显得尤为重要。

机器人是可以代替人工的智能化装置，也是我国研究的重要领域。现有机器人绝缘处理裸导线的方式主要分为3种：包裹式机器人、缠绕式机器人及涂覆式机器人。缠绕式机器人需对缠绕后的绝缘带进行加热收缩，加热过程可能会影响导线性能[5]。包裹式机器人电工胶布安装不牢固，需要人工上线安装[6]，且胶布卷材体积过大，运行中易触碰其他导线而引起事故。涂覆式机器人主要采用绝缘涂料进行带电作业，可以利用小体积料筒实现长距离绝缘处理功能，但存在漏胶缺胶问题，影响涂覆质量[7-8]。

针对以上问题，本文作者设计一种轻型架空线路绝缘涂覆机器人并分析其注胶系统。将注胶系统结构及注胶压力作为变量，设计注胶系统正交仿真试验。使用极差分析法分析多因素作用下的注胶模出口流体速度、注胶流体速度稳定性及胶管出口压力的影响程度和变化形势，并利用多目标遗传算法(MOGA)对该问题进行多目标优化求解，获得能实现较优涂覆效果的注胶系统结构与工作参数。并结合研究所得进行机器人样机试制，经过机器人行走、涂覆及涂覆后导线耐压测试[9]，表明机器人运行可靠，涂覆质量良好。

1 涂覆机器人机械结构

该涂覆机器人的机械结构主要由导线行走装置、涂料注胶系统、机器框架及软连接四部分组成。机器人主要依靠导线行走装置实现在架空导线上的移动，裸导线包覆绝缘涂料作业则由涂料注胶系统完成。作业时，涂覆机器人由作业人员乘坐绝缘斗臂车放置安装于裸导线上，之后作业人员利用远程遥控的方式控制行走轮运动及喷涂装置注胶，以实现涂覆作业。涂覆机器人结构如图1所示。

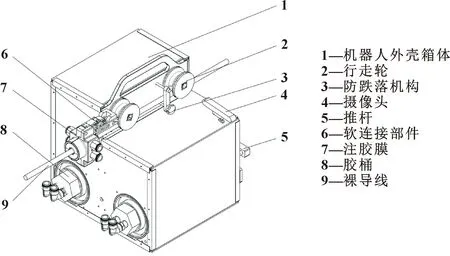
图1 涂覆机器人结构

1.1 导线行走装置

机器人行走装置采用双轮独立驱动，选用体积小巧、定位精度高的伺服一体电机配上大减速比的谐波减速器，能有效驱动行走轮，使机器人在裸导线上运行稳定。电机通过非标连接件与谐波减速器固定，谐波减速器利用螺栓连接安装于固定板上。行走轮内孔安装定制套筒，减速器输出轴与套筒使用键连接。行走轮采用V形轮结构，V形轮能适应一定范围内的不同裸导线线径，选用聚氨酯材料并做花纹轮面，以增大V形轮与导线之间的摩擦力，提高机器人爬坡运行中防打滑能力[10]。

1.2 涂料注胶系统设计

涂料注胶系统是涂覆机器人的核心结构，由注胶模块、胶桶、滚珠丝杆螺母副、快插接头、同步带及减速直流无刷电机组成，如图2所示。涂料喷涂装置参照注射器压力式供胶原理设计，减速电机固定于中间连接板上，减速电机与丝杆螺母副通过同步带轮传动，推杆通过滚珠丝杆上的非标件与螺母副连接。减速电机经同步带传动系统带动丝杆转动并前后移动，丝杆传动时带动推杆推动绝缘胶桶末端的密封活塞，将绝缘胶匀速挤出胶桶口。胶桶口与注胶模之间利用PL、PC快插接头及注胶管导通，使得绝缘胶能均匀注满注胶模块。绝缘胶桶固定于胶桶固定外壳内，用于存储绝缘胶。

图2 螺杆注射式结构

1.3 高黏度绝缘注胶模设计

新型的高黏度绝缘注胶模经软连接与移动车体相连，结构如图3所示。裸导线从其中心穿过，该注胶模采用两半对称机械结构，以便套设在裸导线上。采用铁氟龙材料注塑加工喷头内芯、采用光敏树脂材料3D打印定位芯，铁氟龙及光敏电阻材料均具有良好的不黏性、绝缘性及润滑性，确保了绝缘胶在喷涂阶段不会粘到注胶模上。注胶模内芯与定位芯之间采用弹簧弹性固定4个均布安装的卡线定位销。根据裸导线线径不同，定位销弹簧形变量改变，以实现对导线自适应定位。在电力线行走方向，喷头内腔设计有特定内倾角以刮涂胶料。注胶模经过4根对称的胶管接头导入绝缘胶，以实现绝缘胶的均厚和匀速涂覆。

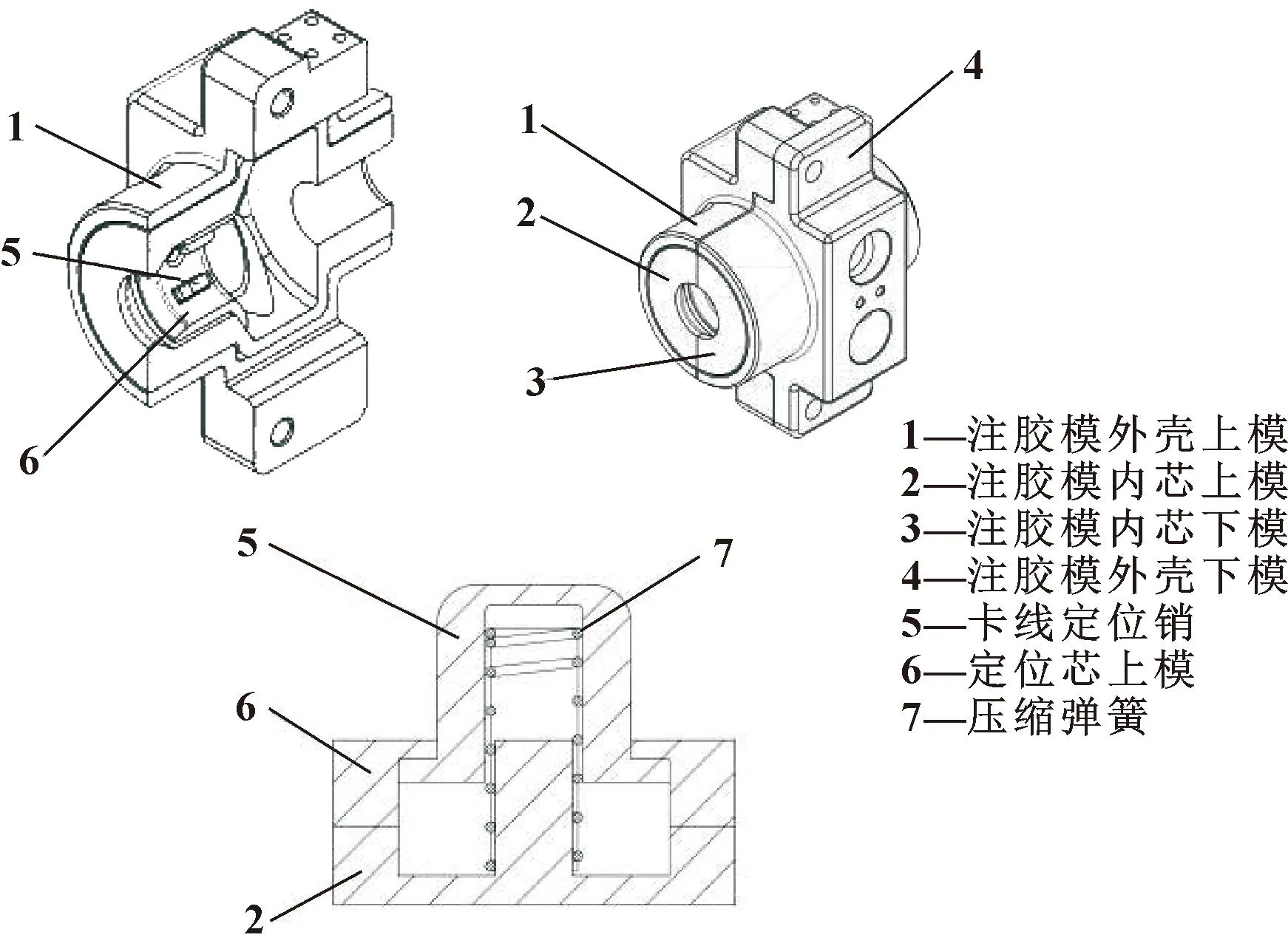
图3 高黏度绝缘注胶模结构

2 注胶系统优化分析

2.1 数学模型

2.1.1 挤压流动过程的控制方程

流体挤压流动满足质量守恒定律、动量守恒定律和能量守恒定律。

微分法是对质点及空间进行研究的方法，可用于解决复杂的流体流动问题。故以微分形式的三大基本定律作为硫化硅橡胶挤压流动的控制方程[11]。

2.1.2 基本假设

考虑仿真计算的收敛性问题，对硫化硅橡胶流体的稳态流动提出如下基本假设：

(1)硫化硅橡胶在流域的流动是稳态层流，且环境温度为恒温。

(2)硫化硅橡胶在流域的流动不可压缩。

(3)硫化硅橡胶的黏性很大，忽略重力影响。

2.1.3 本构方程

硫化硅橡胶属于不可压缩的非牛顿体，根据相似原则及试验要求，将硫化硅橡胶取作幂律流体[12]，其公式如下：

τ=k(λγ)n-1

(1)

式中：τ为剪切应力，Pa·s；k为黏稠系数，也称幂律系数，Pa·s；γ为剪切速率，s-1；λ为松弛时间，s；n为流性指数。

2.2 注胶系统的结构设计

基于注射器式压力注胶挤出过程中，硫化硅橡胶在注胶桶活塞的恒压力作用下，以稳定的流率通过胶管注入注胶模中，实现挤出。注胶装置物理模型如图4所示。

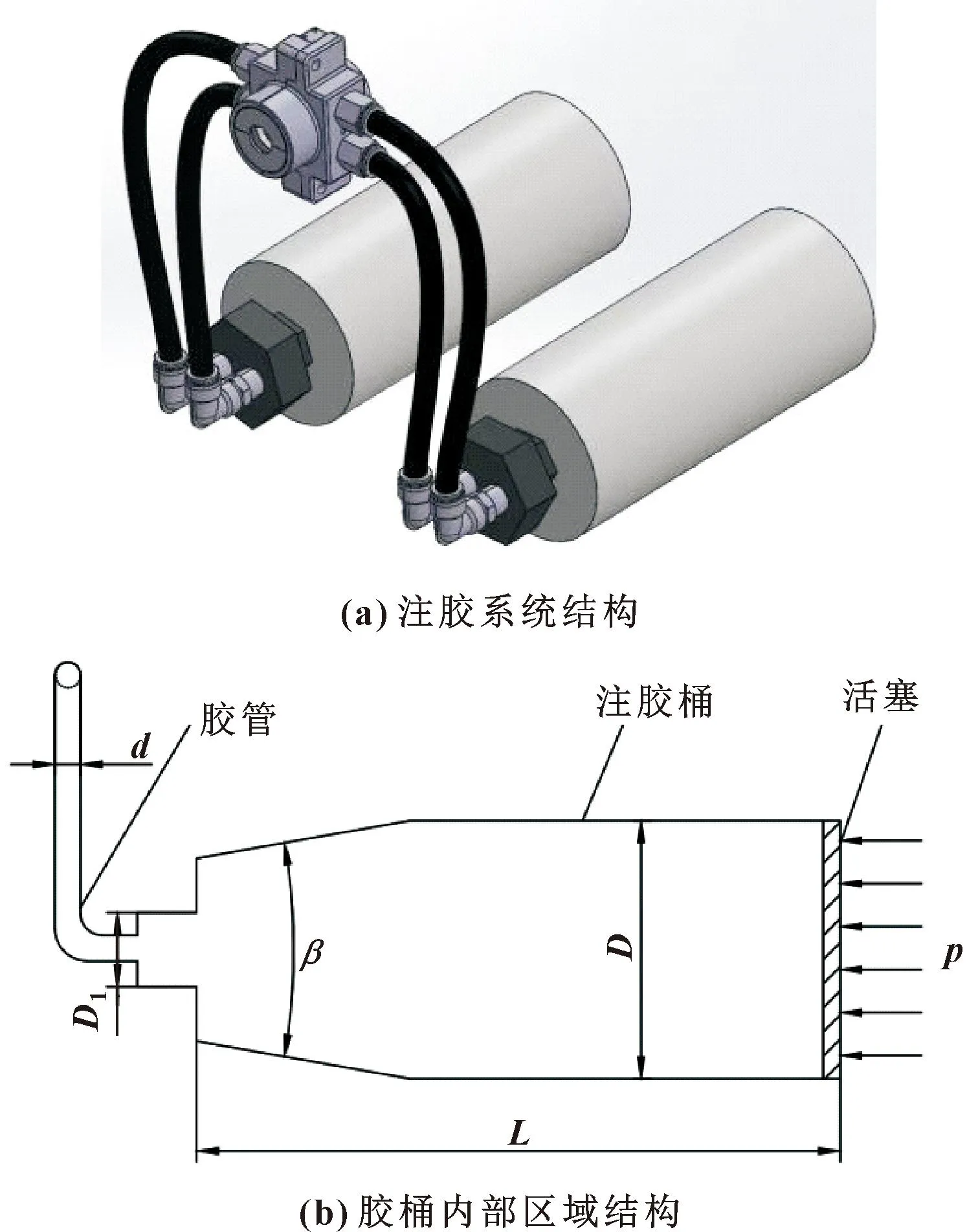
图4 注胶装置物理模型

2.3 正交试验设计

通过对比胶筒结构尺寸、胶管内径对注胶性能及胶体流量的影响，选出性能较优的结构，以达到注胶模块送胶连续、出胶效率高的目的。通过分析喷涂装置注胶挤出影响因素，主要从3个因素(注胶桶收敛角β、注胶压力p和胶管内径d)进行仿真试验。依据表1进行L9(34)正交试验设计。其中胶桶入口直径D、胶桶出口直径D1和胶桶长度L为常数，D=120 mm，D1=60 mm，L=300 mm。

表1 注胶影响因素水平

2.4 流域仿真试验

2.4.1 流域网格划分

绘制9组正交试验所需的注胶系统模型，对试验5注胶模型进行网格划分，由于该模型结构复杂，故采用四面体网格划分方法。细化注胶系统双出口网格，流域区域外壁设置膨胀层，以提高仿真精度。模型及网格见图5。

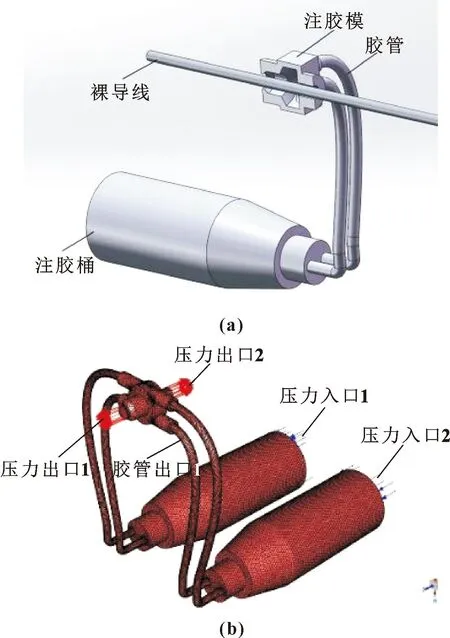
图5 注胶系统模型(a)及流域网格(b)

2.4.2 边界条件设置

依据正交试验方案，使用Fluent软件对设计的9种流道模型进行仿真计算。试验材料选用改良后的室温固化硫化硅橡胶(RTV)[13]，其相关参数如表2所示。机器人在实际工作中，注胶桶和胶管相对位置保持不变，即相对速度为零，故采用压力差模型[14]。边界条件设置入口为压力入口，压力值为1.8×105～2.0×105Pa；出口为压力出口，压力值为大气压。流体为不可压缩的非牛顿体，设置为层流[15]。流体壁面温度为室温，并假设壁面与流体无滑移。

表2 RTV材料相关参数

2.5 仿真分析

2.5.1 仿真结果

正交仿真试验结果如表3所示，重点以注胶模出口(此出口指压力出口1)流体速度均值v、速度标准差σ及胶管出口压力(此出口指胶管出口1)值p1作为研究对象。9组仿真试验速度场、压力场分布状态相似。以试验5为例，仿真结果见图6。由图6(a)可以看出：注胶模流道速度总体稳定，随流体流向注胶模压力出口1的沿程速度逐渐提高。由图6(b)(c)可以看出：因流道壁面流体产生黏性阻力，导致管内流速大于管壁流速。由图6(d)(e)可以看出：胶管出口压力稳定，胶管出口1的压力略大，沿程压力在胶体流向胶管出口的方向上逐渐减小。

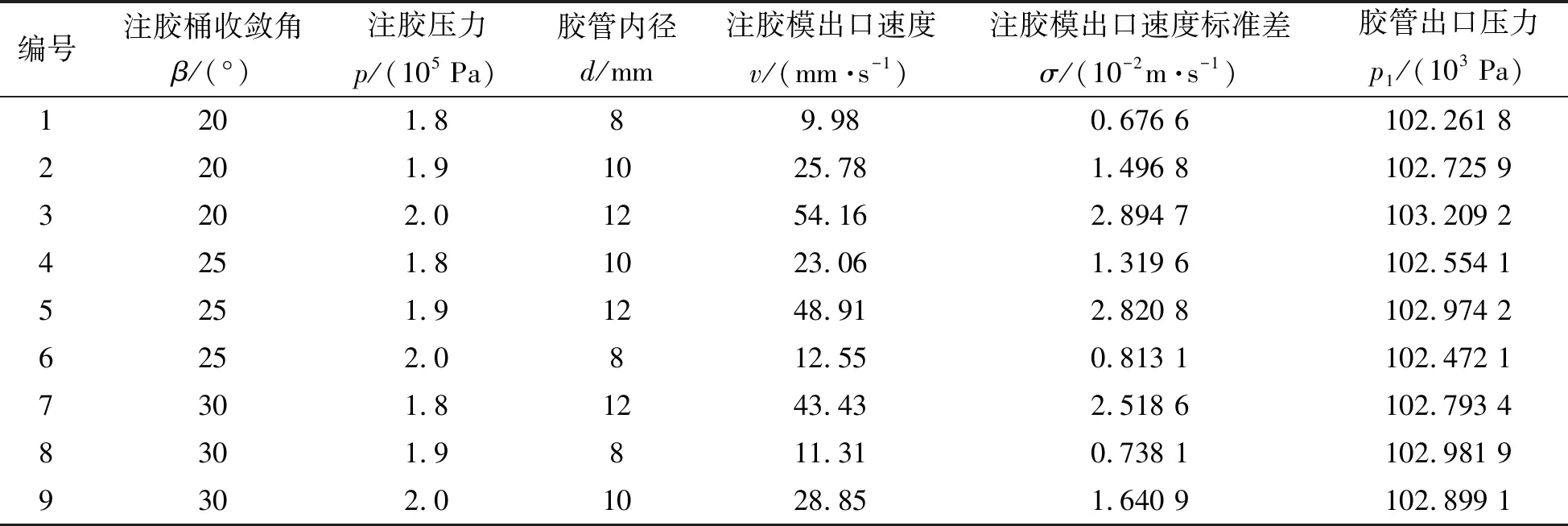
表3 正交仿真试验结果

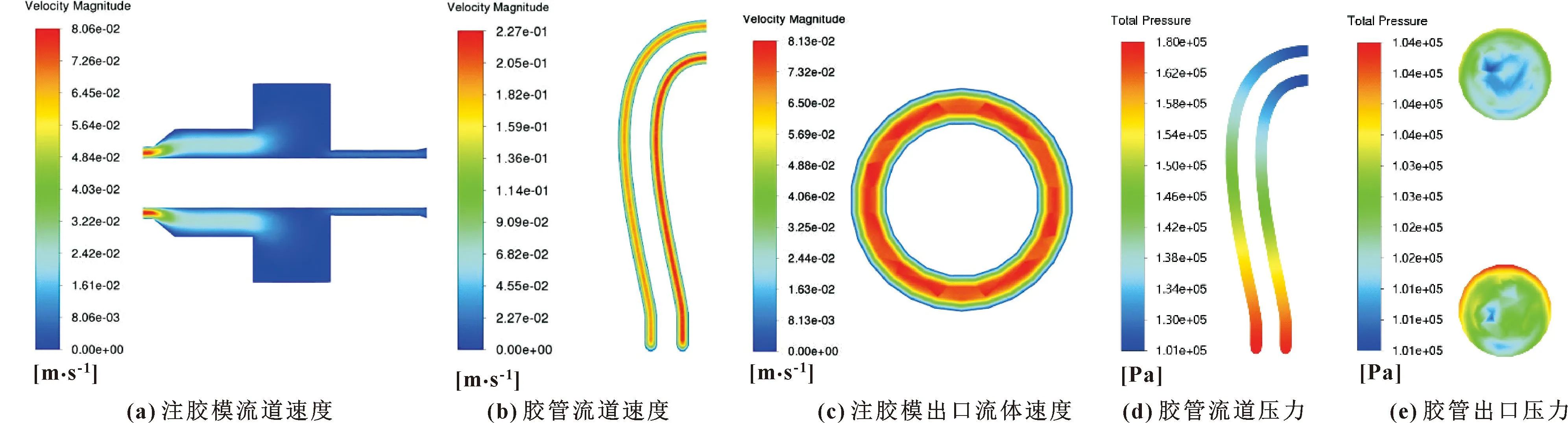
图6 试验5仿真结果

2.5.2 极差分析

极差分析法是一种操作性强、具有主观性的分析方法。通过计算R值来判断因素的优劣情况，同时还可判断某因素时的最佳水平情况，从而得到理想组合。

计算公式如下：

(2)

(3)

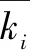
2.5.2.1 注胶模出口流体速度分析

由公式(2)(3)计算获得注胶模出口流体平均速度的极差分析结果，见表4。可得：胶管内径对出口流体速度均值影响显著，胶管内径与出口速度均值成正比关系。分析可得：相同压差情况下，由于硫化硅橡胶为不可压缩流体且黏度较大，管壁周围对流体有黏性阻力，导致管壁流速低于管内速度，从而使平均速度降低。管径越大，黏性阻力影响越小，平均流速越大。但考虑到胶管制造的工艺性，胶管内径不能超过12 mm。

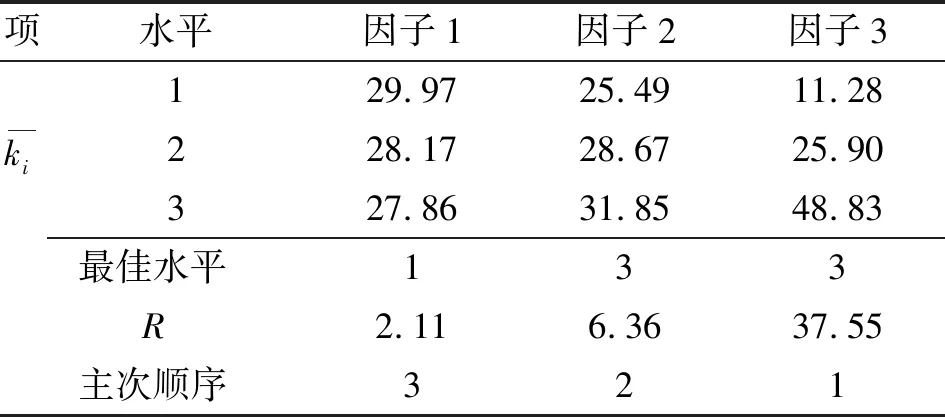
表4 注胶模出口流体速度均值极差分析结果

2.5.2.2 注胶模出口流体速度标准差值分析

同理，可得注胶模出口流体速度标准差值的极差分析结果，见表5。可得：与其他因子相比，胶管内径对出口速度标准差值具有明显影响，随着胶管内径的增大，出口速度标准差值也随之增大。说明较小的管径有利于流体稳定流动，但考虑到胶管的制造工艺性，胶管内径不能小于4 mm。同时，其他因子对注胶模出口流体速度标准差值没有显著影响。

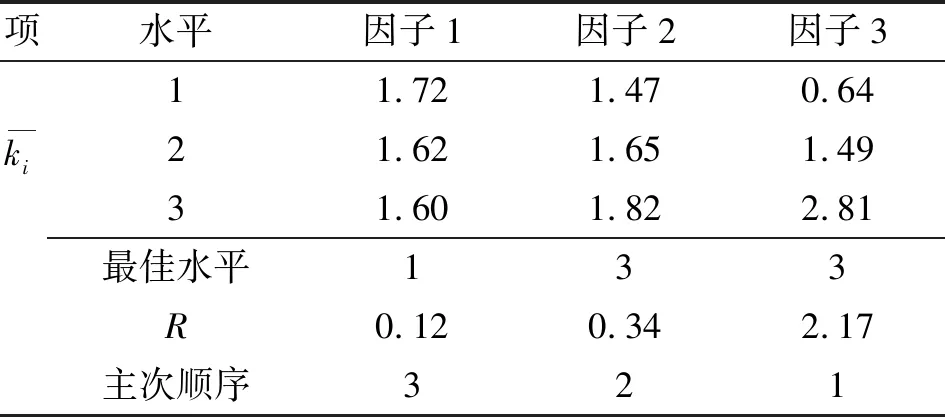
表5 注胶模出口速度标准差值极差分析结果

2.5.2.3 胶管出口压力分析

同理，可得胶管出口压力的极差分析表，见表6。可得：三因子对胶管出口压力具有不同程度的影响，影响程度由大到小依次为注胶压力、注胶桶收敛角、胶管内径。当注胶压力上升时，胶管出口压力也上升。考虑到压力越大流体更易从胶管挤出至注胶模，故尽可能选择较大的注胶压力。

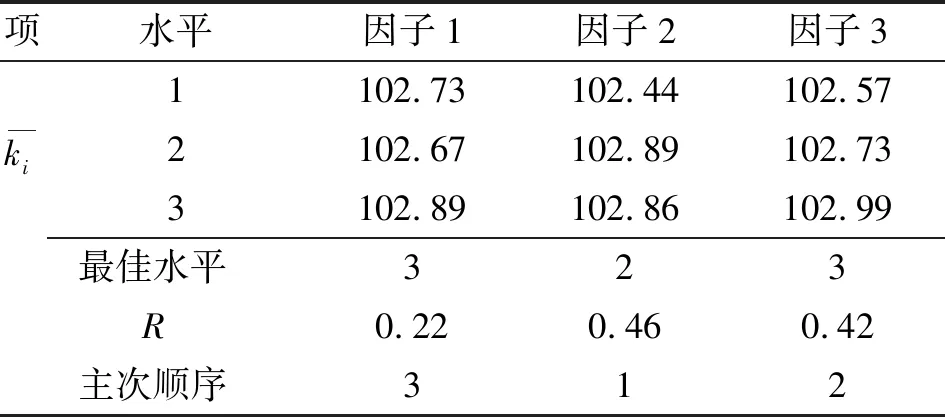
表6 胶管出口压力极差分析结果

通过以上分析可知，试验因素对注胶模出口流体速度均值、速度方差及胶管出口平均压力的影响程度各异。综合考虑，将优化指标选为较高注胶模出口流体流速(v≤50 mm/s)和胶管出口压力、较低速度标准差值，通过MOGA算法进行优化求解。

3 基于多目标遗传算法的优化设计

3.1 多目标遗传算法原理

多目标遗传算法(MOGA)具有全局搜索性，收敛速度快，可解得一系列的帕雷托解，并非是单一解。多目标遗传算法运算流程[16]如图7所示。

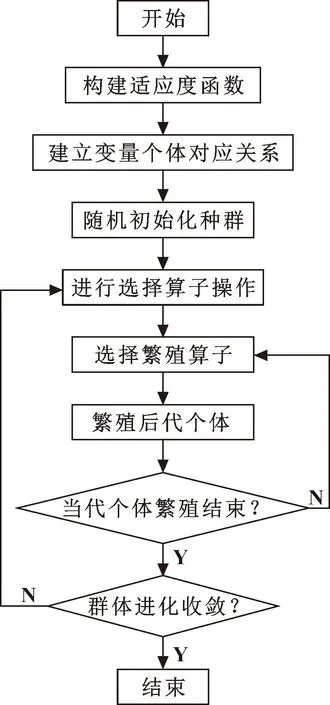
图7 MOGA算法流程

3.2 优化方法

多目标优化问题是现实各个领域中普遍常见的问题，各目标相互限制，不可能同时达到最优。传统多目标优化算法在寻优过程中往往会陷入局部最优解，故结合具有全局搜索能力的遗传算法进行求解，可以得出各指标相对具有优势的解集。定义多目标优化问题如式(4)(5)所示：

minF(x)=[f1(x),f2(x),…,fm(x)]Tx∈Rn

(4)

s.t.hi(x)≤0i=1,2,…,q

(5)

式中：x=[x1，x2，…，xn] ∈Rn，为n维欧氏设计变量；F(x)为n维目标函数；fi(x)为适应度函数，i=1，2，…，m，m∈R+；hi≤0为第i个约束条件；q为约束个数。

3.3 建立适应度函数

建立遗传算法适应度函数对多目标优化问题进行求解计算[17]。试验中优化指标为注胶模出口流体速度均值、速度标准差及胶管出口平均压力，并使用MATLAB软件对9组试验数据进行多项式拟合分析。为获得良好拟合程度的回归方程，将多项式最高次项设置为3次[18]，从而分别得到β、p和d的3个回归方程。

建立注胶模出口流体速度均值回归模型：

v=90.128 1+4.728 5β-82.788 9p-0.965 1βd-

0.000 218 64β3+2.703 2p2d+0.04βd2+0.050 4βpd

使用联合假设检验法对回归方程进行检验，F0.1(7,1)=2.24×103，大于临界值F0.1(7,1)=58.906，回归方程可用。

建立注胶模出口流体速度标准差值回归模型：

σ=4.152 7+0.259 2β-4.448 5p-0.053 9βd-

0.000 010 56β3+0.149 1p2d+0.002 5βd2+0.002 4βpd

使用联合假设检验法对回归方程进行检验，F0.1(7,1)=1.307×105，大于临界值F0.1(7,1)=58.906，回归方程可用。

建立胶管出口压力回归模型：

p=105.542 1+0.178 5β-4.113 7p-0.018 9βd+

0.000 049 52β3+0.163 5p2d+0.000 505 7βd2-0.005 8βpd

使用联合假设检验法对回归方程进行检验，F0.1(7,1)=253.98，大于临界值F0.1(7,1)=58.906，回归方程可用。

3.4 目标函数

建立自变量优化模型矢量表达式如式(6)所示，自变量为注胶桶收敛角β、注胶压力p和胶管内径d。

x=[β，p，d]T=[x1，x2，x3]T

(6)

令注胶模出口流体速度、速度标准差、胶管出口压力回归方程分别为y1(x)、y2(x)和y3(x)，优指标选用较大的注胶模出口流体速度、胶管出口压力和较小的注胶模出口流体速度标准差，使用最小值求解法。使注胶模出口流体速度、胶管出口压力取最大值，即min(-y1(x))、min(-y3(x))。使注胶模出口流体速度标准差取最小值，即miny2(x)。目标优化函数如式(7)所示：

minf(x)=[-y1(x)，y2(x)，-y3(x)]T

(7)

3.5 约束条件

基于正交试验参数的选取范围对自变量x1、x2、x3取值范围进行约束，注胶桶收敛角范围如式(8)所示，注胶压力范围如式(9)所示，胶管内径范围如式(10)所示：

(8)

(9)

(10)

故自变量x1、x2、x3取值边界约束条件如式(11)所示：

h(x)=[h1(x),h2(x),h3(x)]T

(11)

综上，求解注胶系统结构多目标优化问题的模型为

(12)

3.6 求解最优解集

根据注胶系统设计要求，确定注胶系统结构及工作参数取值范围如式(13)所示。使用MATLAB软件调用多目标遗传算法函数文件进行求解，所得Pareto前端最优解集如图8所示。

(13)

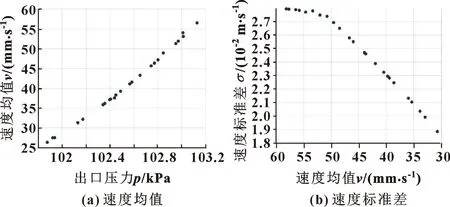
图8 Pareto前端最优解集

3.7 优选结果

分析结果可得：注胶模出口流体速度均值与胶管出口压力成正比；速度标准差随注胶膜出口流体速度增大而增大，当速度大于52.25 mm/s时趋近于同一值。为解决注胶模漏胶缺胶问题，应优先考虑较大出口速度。故解集优选参数为注胶桶收敛角22°～23°、胶管内径12 mm、注胶压力(1.9～1.95)×105Pa。表7中列举了上述优选参数的仿真计算结果。可知：(1)胶管出口压力处于较高水平，说明胶管内流体有较好的流动性，有利于胶体挤出进入注胶模；(2)注胶模出口流体速度处于较高水平，保证了在涂覆过程中流体不会挤出注胶模影响涂层厚度，提高了涂覆质量；(3)注胶模出口流体速度标准差处于较低水平，说明流体具有良好的稳定性，提高了涂覆精度。

4 样机运行情况

选取上述注胶系统结构及推杆压力，制作样机并进行现场试验，总结绝缘涂覆机器人的主要技术指标，如表8所示。

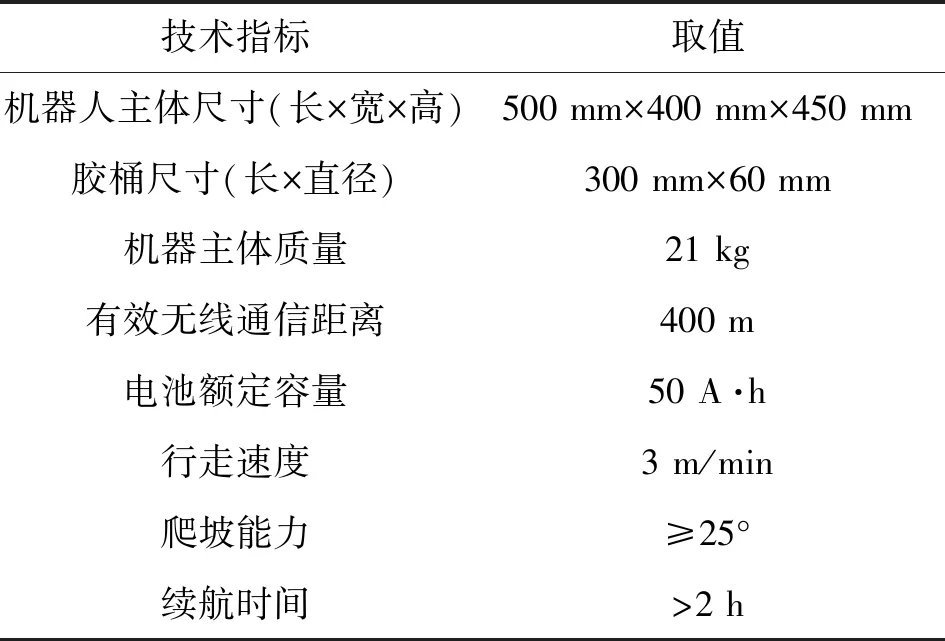
表8 技术指标

针对涂覆机器人涂覆效果和行走能力，在模拟线路和实际线路上进行试验，并对涂覆后电缆进行耐压试验。试验结果表明：采用双轮驱动方式为机器人提供了足够的动力，机器人行走过程稳定；考虑制作工艺及工况需求，采用注胶收敛角约23°、注胶压力约1.925×105Pa和12 mm线径的注胶系统结构，涂覆过程中注胶模未出现漏胶和缺胶的情况，涂覆效果良好；行走轮采用V形轮结构，能适应不同线径；各机构电机转速适配，维持一定的线性关系，使涂覆机器人行走速度达到3 m/min；两个胶桶对称放置于机器人底部，保证机器人重心稳定，有效避免机器人在大风情况下发生倾覆。涂覆后电缆在45 kV直流耐压试验中，1 min内未发现击穿现象，满足GB/T 34577—2017标准要求。机器人样机行走和电缆涂覆后耐压试验如图9所示。

图9 样机试验

5 结论

本文作者设计一种轻型绝缘涂覆机器人，用于覆盖架空裸导线。并利用ANSYS Fluent软件，对机器人注胶系统进行流域正交仿真试验。以提高涂覆质量和注胶模内黏性流体流动性为目标，以注胶桶收敛角、注胶压力与胶管内径为试验变量，并以较小的注胶模出口流体速度标准差和较大的胶管出口压力、注胶模出口流体速度均值为优化指标，通过对比流域云图，得出注胶系统压力场、速度场的分布趋势。并对比流场仿真数据，得出以下结论：

对正交仿真试验结果进行极差分析，得到每个指标在不同因素作用下的变化趋势。其中，注胶压力是胶管出口压力均值最显著的影响因子。注胶模出口流体速度均值、标准差最显著的影响因子是胶管直径。

基于多目标遗传算法对注胶系统结构进行多目标优化求解，并考虑注胶系统实际的工艺性，得出在注胶桶收敛角22°～23°、胶管内径12 mm、注胶压力(1.9～1.95)×105Pa的情况下，注胶系统工作性能较优。

最后依据上述较优注胶系统结构参数进行样机制作，并进行模拟线路及实际线路的试验，试验结果表明样机运行及涂覆性能良好。