基于稀疏节点与双向插值的RRT*改进算法
王国安,姜春英,陶广宏,叶长龙
(沈阳航空航天大学机电工程学院,辽宁沈阳 110136)
0 前言
随着机器人技术的不断发展,路径规划作为智能机器人技术发展的关键,得到了高速的发展。路径规划研究的问题可以描述为:在地图环境已知或部分已知的情况下,规划一条起点到目标点且与障碍物无碰撞的有效路径。根据地图环境的状况,路径规划算法可以分为全局路径规划和局部路径规划。常用的路径规划算法主要有以下几种:图搜索算法[1]、人工势场法[2]、基于随机采样的算法[3]、智能算法[4-6]和融合深度学习的算法[7]等。
RRT算法是基于采样的算法中典型代表之一[8]。RRT算法通过随机采样在空间中获取一组离散点,经过碰撞检测,进而形成一条无碰撞路径。与传统路径规划算法相比,RRT算法具有概率完备[9]、易于实现等优点,但由于没有考虑路径的长度问题,往往生成的路径较为曲折,不能保证结果为最优路径或次优路径。因此,众多学者也为之开展了许多探索与研究。一方面,为了加快算法收敛速度,文献[10]提出了RRT-Connect算法,其改进点在于同时从起点和目标点建立随机树并扩展,同时也提出了一种多树扩展思想,加快了算法收敛速度;文献[11]中的Bias-RRT算法通过生成随机树的随机样本的概率分布影响算法的收敛速度,将目标点以更高的概率添加到分布中,这种方法极大地提高了算法向目标点的扩展速度;另一方面,为了得到最优或近优路径,文献[12]提出了RRT*算法,核心在于选择最优父节点和重连两个优化过程,进而通过不断迭代得到最优解,但此算法仍然存在计算时间长的不足;文献[13]和文献[14]分别提出了Informed RRT*算法和RRT*-SMART算法,前者提出超球概念来缩小节点采样范围,后者则通过选择关键节点来限制节点采样范围,均可以在一定程度上加快收敛速度;文献[15]提出了随机树被动生长方法,与引力函数相结合,提高了算法的运行速度;文献[16]提出的Q-RRT*算法,通过三角不等式可大量跳过路径中不必要的冗余节点,进而极大地缩短了路径长度,达到次优路径。文献[17]提出了一种目标偏置扩展和CantmullRom样条插值的双向RRT*路径规划算法,缩短路径的同时对路径进行了平滑处理。文献[18]提出一种基于跳点搜索(JPS)策略的RRT*算法,通过跳点搜索策略减少寻路过程中计算节点的数量,提高了RRT*算法的搜索效率,加快了收敛速度。
以上述文献为基础,针对RRT*算法存在的精度低、环境适应性差等问题,本文作者提出了一种基于稀疏节点与双向插值的RRT*改进算法,并通过仿真实验验证了该算法的有效性。
1 问题与方法描述
1.1 问题描述
路径规划中,一般把整个空间定义为X。根据与障碍物之间的状态,又划分为Xobs和Xfree,Xobs代表障碍物区域;Xfree代表无障碍物区域,且Xfree=X/Xobs。将(X,xstart,xgoal)定义为一个路径规划问题,其中xstart∈Xfree为初始状态,xgoal⊂Xfree为目标区域。在此前提下,通过已知的(X,xstart,xgoal),得到一条从xstart到xgoal的无碰撞路径。
1.2 标准RRT*算法
RRT*算法是通过树T=(V,E)的形式来探索空间,其中V是节点的集合,E是节点之间连接关系的集合。RRT*算法首先通过随机采样函数Sample()在地图Map上得到随机点xrand;使用Nearest(V,xrand)寻找,获得距离xrand最近的点xnearest;如果xrand与xnearest的距离大于ε,则以步长ε扩展新节点xnew,否则使用原距离扩展新节点xnew;如果xnew和xnearest之间与障碍物未发生碰撞,则找出xnew的邻域Vnear,通过ChooseParent(Vnear,xnew)函数在邻域Vnear中重新选择xnew的父节点,若Vnear中存在点使得xstart到xnew的路径距离更短,则替换xnew的父节点,否则不操作;再通过Rewire(Vnear,xnew)函数进行重新布线,若Vnear中的点的父节点改为xnew可以缩短路径,则进行父节点更新,否则不操作。迭代优化过程赋予RRT*算法渐进最优性[12]。RRT*算法的伪代码如算法1所示。
算法1 RRT*
Input:xstart,xgoal, Map
Output:T=(V,E)
1: fori=1 toKdo
2:xrand=Sample();
3:xnearest=Nearest(V,xrand);
4:xnew=NewNode(xnearest,xrand,ε);
5: If CollisionFree(xnew,xnearest, Map)then
6:Vnear←Near(T,xnew,rnear);
7:xparent←ChooseParent(Vnear,xnew);
8:T←E(xnew,xparent);
9:T←Rewire(Vnear,xnew)
10: end if
11: end for
2 改进RRT*算法
在RRT*算法中,采样点在空间均匀采样,使得算法向目标点扩展速度慢;并且,在迭代过程中,随机树节点大量增加,算法计算量明显增大,导致算法效率低下。针对RRT*算法存在的收敛速度慢、效率低等问题,本文作者提出了基于稀疏节点与双向插值的RRT*改进算法。
改进算法在找到初始路径前,首先依据目标偏向策略确定好采样点;再根据步长获取新节点;通过稀疏节点法提前判断新节点是否满足扩展要求,避免算法在局部区域过度搜索;在找到初始路径后,通过双向插值优化,对路径进行优化迭代;在达到迭代次数上限或运行时间上限后,视为达到收敛目标,终止迭代。改进的RRT*算法流程如图1所示。
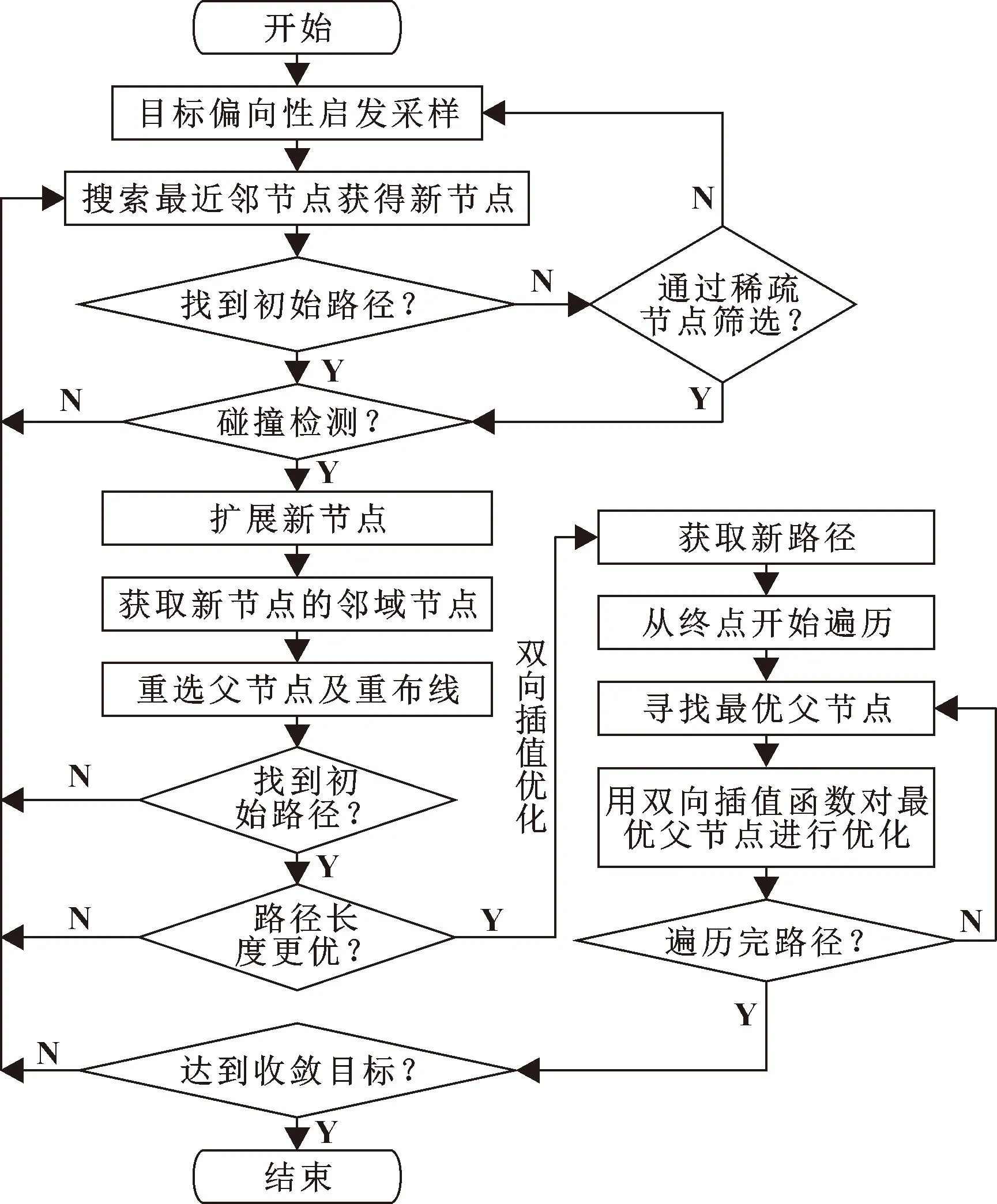
图1 改进算法流程
2.1 目标偏向采样
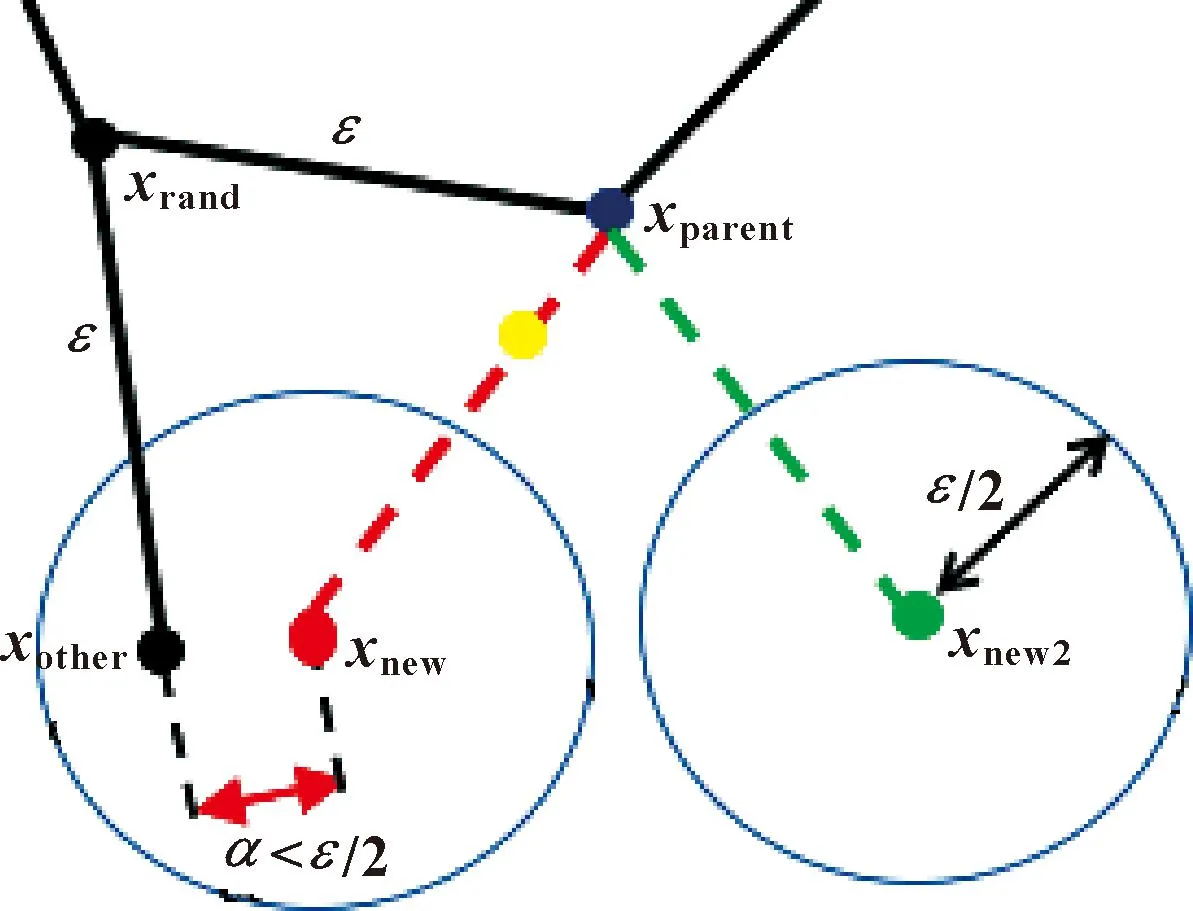
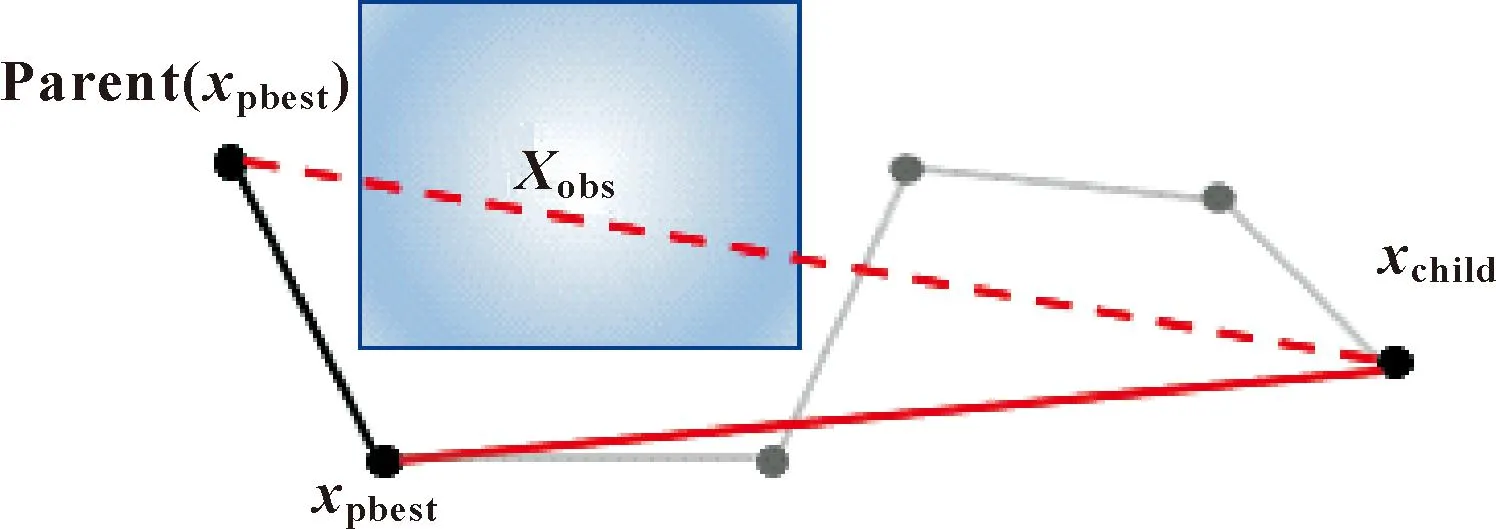
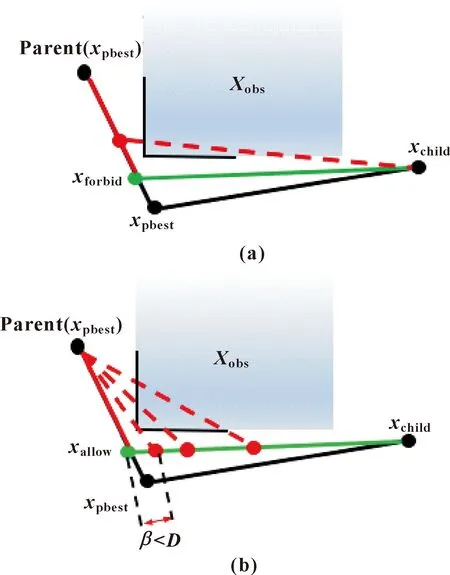
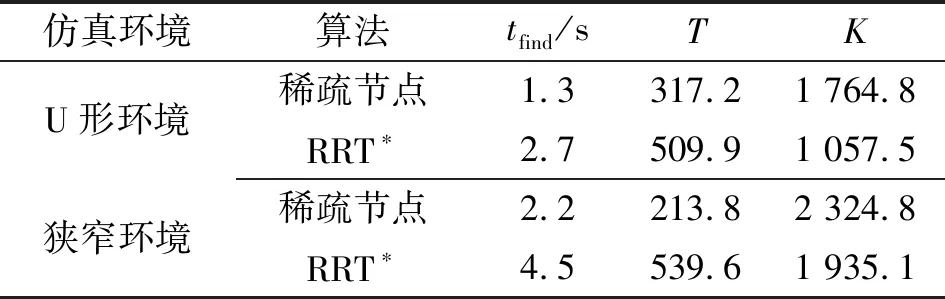
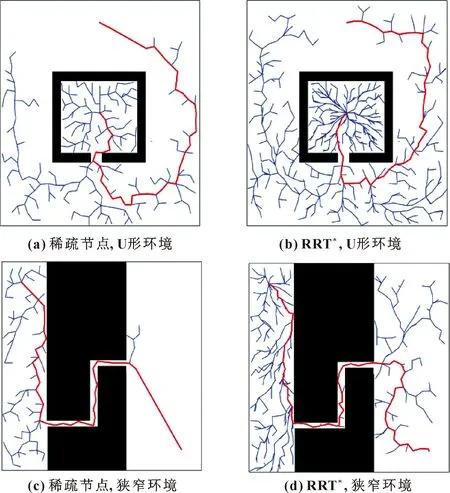
鉴于RRT*算法所获得的采样点存在随机性与盲目性,使得算法搜索效率低,本文作者采用目标偏向采样[11],使随机树在采样过程中,以一定的概率朝着目标点生长。目标偏向采样的具体内容为:首先,设置目标偏向概率阈值Q(Q∈(0,1)), 采用高斯随机数Qrand(Qrand∈(0,1))与上述概率阈值Q相比较。当Qrand 在RRT*算法中,经过多次迭代,随机树节点扩展的随机性会使得局部区域被节点重复扩展,造成局部区域内节点过多。若对节点扩展不加以限制,将导致算法迭代时间增多,算法效率下降。故本文作者采用稀疏节点法对节点扩展加以限制,避免节点在局部区域内过度搜索、重复扩展,增强算法的搜索效率,以此来缩短获得初始路径的时间。 如图2所示,对节点xnew进行稀疏节点筛选,判断该节点是否为可扩展节点。经过目标偏向采样得到xrand后,先得到其最近节点xparent;再以xparent为父节点,ε为步长,向xrand方向扩展得到xnew;此时,以xnew为中心,以ε/2为半径画圆,若圆内存在其他已扩展节点,则xnew未通过节点筛选;而以xnew2为中心,以ε/2为半径画圆,圆内无其他节点,则xnew2通过筛选。 图2 稀疏节点法示意 此改进算法中,稀疏节点法的伪代码如算法2所示。 算法2 Choosepoint(T,xnew) 1:xnewnear=Nearest(V,xnew); 2: if |xnew-xnewnear|<ε/2 then 3: return False; 4: else 5: return True 6: end if 通过RRT*算法得到的初始路径往往较为曲折,同时依然存在大量的冗余节点。因此,需对该路径进行优化处理,以便获得更加平稳的路径。鉴于此,本文作者采用三角不等原理与双向插值算法对路径进行优化,以获得最优的路径规划结果。 该优化过程存在两个核心过程:(1)重新选择路径中节点的父节点,去除路径中的冗余节点,该过程定义为算法3中的最优父节点函数FindbestParent(xnode);(2)通过双向插值函数创造一个新的节点,用以代替路径中节点的父节点,使父节点所处的位置更优,该过程被定义为算法3中的双向插值函数SimDic(xnode,xallow, Parent(xnode))。 在最优父节点函数中,以路径中的某一点xchild为例,定义xchild的最优父节点为xpbest,xpbest的父节点为Parent(xpbest)。如图3所示,在寻找最优父节点中,xchild需依次遍历路径上xchild之前的路径节点,在遍历过程中,需进行碰撞检测,若xchild与xpbest之间的路径未发生碰撞,则继续向前遍历节点Parent(xpbest),此时,xchild与Parent(xpbest)之间的路径发生碰撞,则遍历终止,选择xpbest作为xchild的最优父节点。 图3 最优父节点示意 在双向插值函数中,设置参数D为二分法的终止条件,β为算法4中xallow与xgparent之间的距离。 在得到最优父节点xpbest后,以xchild、xpbest和Parent(xpbest)为支点,运用双向插值函数,创建新节点xallow。如图4(a)所示,先以xchild为支点,向xpbest和Parent(xpbest)的连线上,运用二分法与碰撞检测,得到替代节点xforbid;如图4(b)所示,再以Parent(xpbest)为支点,向xforbid和xchild的连线上,在多次二分法寻找后,触发终止条件,则替代节点xallow为xforbid。 图4 双向插值示意 双向插值优化全过程可总结为:在得到xchild的最优父节点xpbest后,运用双向插值函数得节点xallow,若经过优化,则以xallow替换xpbest;同时更新xchild的父节点信息。 路径优化函数PDpath(T)函数的整体流程如算法3所示;双向插值函数的伪代码如算法4所示。 算法3 PDpath(T) 1:xchild=xgoal; 2:xpbest=Findbest Parent(xgoal); 3: whilexpbest≠xstartdo 4:xallow=SimDic(xchild,xpbest, Parent(xpbest)); 5:xallow=SimDic(Parent(xpbest),xallow,xchild); 6: ifxallow≠xpbestthen 7:V(xpbest)=V(xallow); 8: end if 9:E=E∪E(xchild,xpbest); 10:xchild=xpbest; 11:xpbest=FindbestParent(xchild); 12: end while 13: ReturnT; 算法4 SimDic(xnode,xallow,xgparent) 1: while Distance(xallow,xgparent)>Ddo 2:xmid=(xallow+xgparent)/2; 3: if CollisionFree(xmid,xnoed)then 4:xallow=xmid; 5: else 6:xgparent=xmid; 7: end if 8: end while 9: Returnxallow; 对RRT*算法和运用稀疏节点的RRT*算法进行仿真分析,通过仿真实验,验证稀疏节点法在得到初始路径时间和降低随机树节点个数的有效性。 在狭窄、U形环境中,分别对两种算法进行仿真分析。如图5所示,运用稀疏节点的RRT*算法中局部区域中的随机树节点密度更小,稀疏节点法避免了局部区域过度搜索。地图大小为500像素×500像素,步长为20,分别运行50次,得到获取初始路径的时间tfind、随机树节点个数T和迭代次数K,并取平均值得表1。由表1可知,稀疏节点法在寻找初始路径方面,有利于缩短得到初始路径的时间,降低随机树节点个数。 表1 算法对比结果 图5 算法比较 仿真实验配置为:64位Window10,处理器Intel(R)Core(TM)i7-7500U,CPU主频2.7 GHz,内存8 GB。 为了对比文中改进算法的性能,对RRT*、Informed-RRT*、Q-RRT*和文中所述改进算法在3种仿真环境中进行算法验证,如图6所示,地图大小均为500像素×500像素。3种环境下分别将4种算法各运行100次,使用以下4个参数的平均值对算法进行评价:发现初始路径时间tfind、发现次优路径时间t5%、初始路径长度linit以及算法路径长度lpath。 图6 仿真地图 改进算法中参数及变量设置:步长ε设置为20像素,搜索半径rnear为40像素,目标偏向概率Q设置为0.2 ,双向插值距离系数D设为2像素。 3.2.1 仿真环境一 仿真环境一中,xstart设置为[50,50]像素,xgoal设置为[450,450]像素。算法仿真结果如图7所示。 图7 仿真环境一仿真结果 由图7可知:在仿真环境一,文中改进算法路径最优,贴合障碍物边缘;其次是Q-RRT*算法的规划结果;其他两种算法路径较为曲折,存在较多冗余节点。仿真环境一下算法对比结果如表2所示,算法规划的路径长度如图8所示。 表2 仿真环境一的路径规划结果 图8 仿真环境一的路径长度 由表2可知:文中改进算法性能最好,相较于Q-RRT*算法,tfind缩短了71.7%,虽然初始路径linit较长,但次优路径时间t5%缩短了26%;相较于RRT*算法和Informed-RRT*算法,tfind缩短了48.2%和45.5%,t5%缩短了76.5%和67.1%。如图8所示:改进算法得到初始路径的时间最短,并且路径收敛时间最短。 综上所述:在仿真环境一,文中改进算法相较于其他3种算法,tfind、t5%最短;相同时间下,算法收敛时间最快,路径最短。 3.2.2 仿真环境二 仿真环境二中,xstart设置为[50,50]像素,xgoal设置为[450,450]像素,算法仿真结果如图9所示。 图9 仿真环境二仿真结果 由图9可知:在仿真环境二下,文中改进算法性能优于其他3种算法。仿真环境二下算法对比结果如表3所示,算法规划的路径长度如图10所示。 表3 仿真环境二的路径规划结果 图10 仿真环境二的路径长度 由表3可知:文中改进算法性能最好,相较于Q-RRT*算法,tfind缩短了68.4%,次优路径时间t5%缩短了47.2%;相较于RRT*算法和Informed-RRT*算法,tfind缩短了48.4%和46.7%,t5%缩短了72.5%和67.5%。 图10中,RRT*算法和Informed-RRT*算法的曲线几乎重合,这是由于后者的椭球采样优化在迷宫地图中难以发挥作用;文中改进算法路径收敛时间最短。 综上所述,相较于其他3种算法,文中改进算法得到初始路径的时间最短,路径收敛效果最好。 3.2.3 仿真环境三 仿真环境三中,xstart设置为[50,50]像素,xgoal设置为[450,450]像素。算法仿真结果如图11所示。 图11 仿真环境三的仿真结果 由图11可知:在仿真环境三下,文中改进算法性能优于其他3种算法。仿真环境三下算法对比结果如表4所示,算法路径长度如图12所示。 图12 仿真环境三的路径长度 由表4可知:文中改进算法性能最好,相较于Q-RRT*算法、RRT*算法和Informed-RRT*算法,tfind分别缩短了73.8%、55.6%和56.3%,次优路径时间t5%分别缩短了45.9%、70.4%和63%。由图12可知:文中改进算法在收敛速度和路径长度上有较高提升。 基于ROS机器人操作系统,在移动机器人上对文中改进算法进行验证。机器人采用Ubuntu 16.04系统,ROS版本为Kinetic,采用单线激光雷达进行障碍物检测。如图13所示,为改进算法的路径规划图。 图13 改进算法路径规划图 验证过程如图14所示,图中显示了机器人运动的位置。 图14 实际路径规划结果 结果显示:机器人路径规划结果精度较高,机器人可沿着当前规划路径进行无碰撞运动。说明改进算法具有较好的优化能力,对机器人路径规划具有实用价值。 提出一种基于稀疏节点与双向插值的改进RRT*算法。该算法运用稀疏节点法缩短了初始路径寻找时间;在后续迭代中,使用双向插值优化路径节点,有效缩短次优路径时间。 在3种环境下的仿真结果表明:文中改进算法在tfind和t5%上,其平均值分别缩短了约61%和约59%。然后,将所提算法运用在实际机器人路径规划,实验结果表明:改进算法有一定应用价值。文中算法在规划过程中提高了寻路质量和效率,收敛速度更快。2.2 稀疏节点法
2.3 双向插值优化
3 仿真实验
3.1 稀疏节点仿真实验
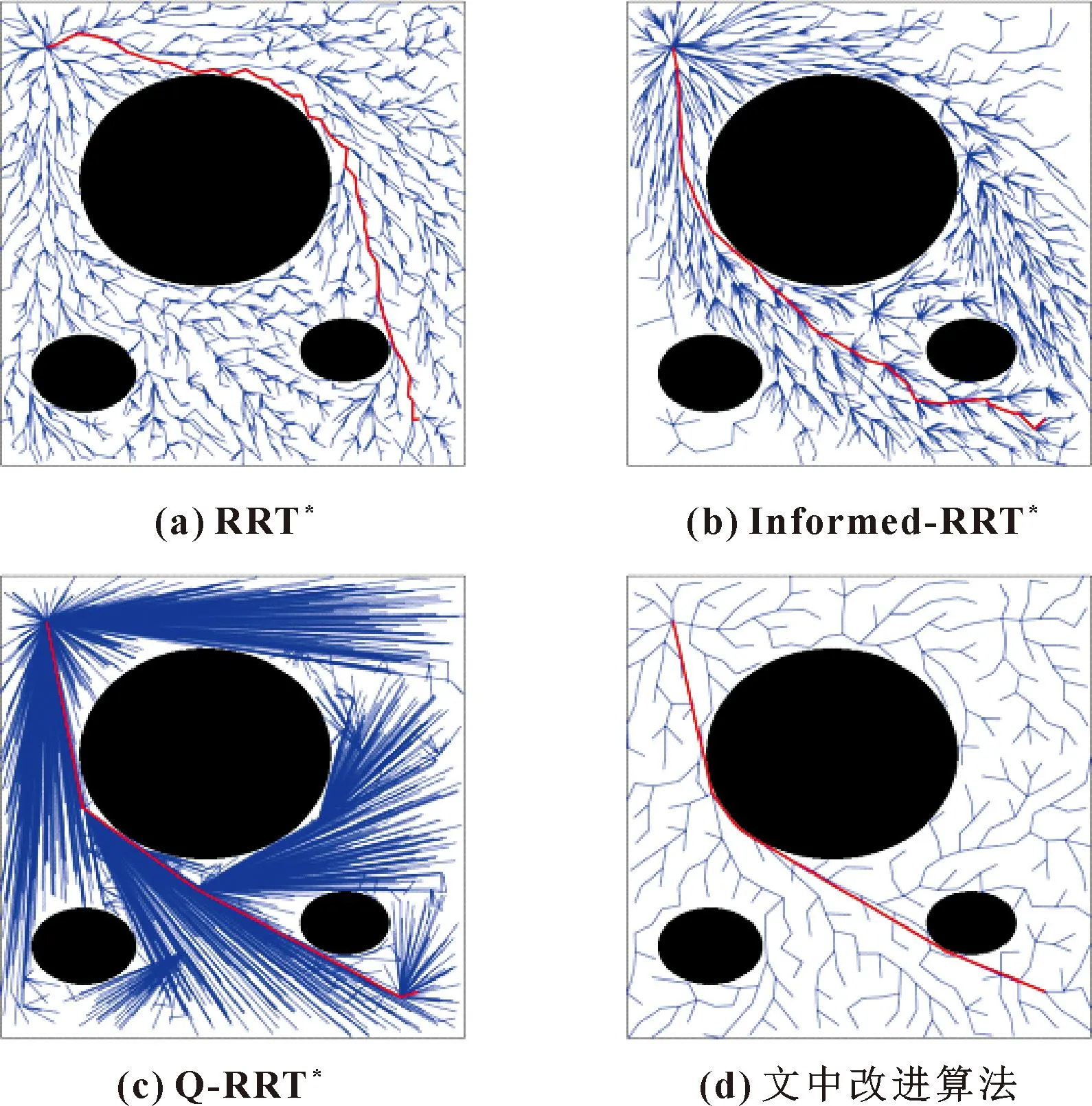
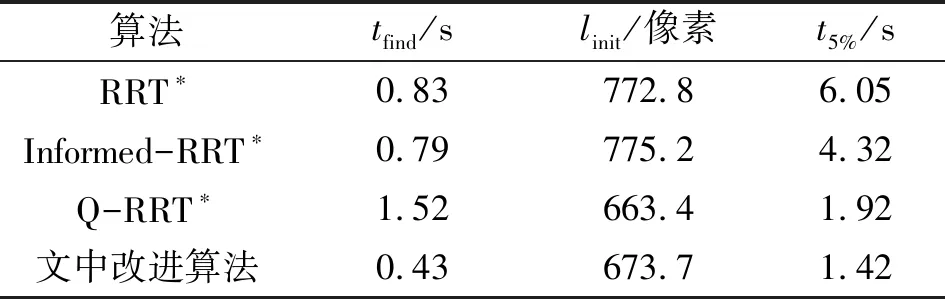
3.2 文中改进算法仿真实验

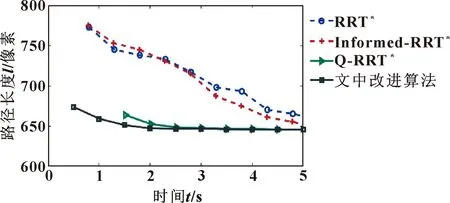

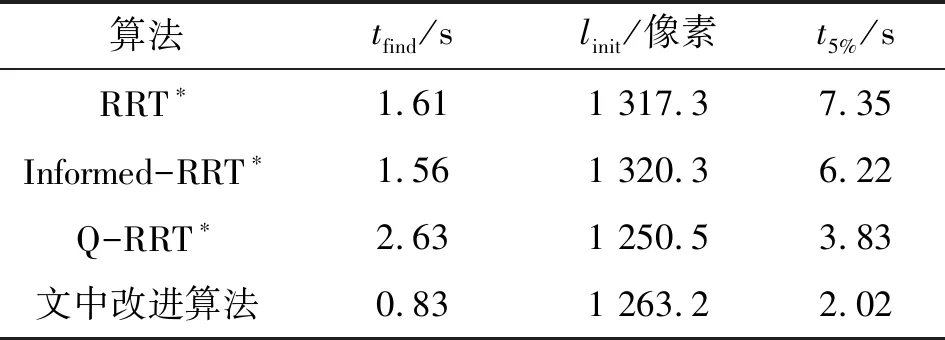
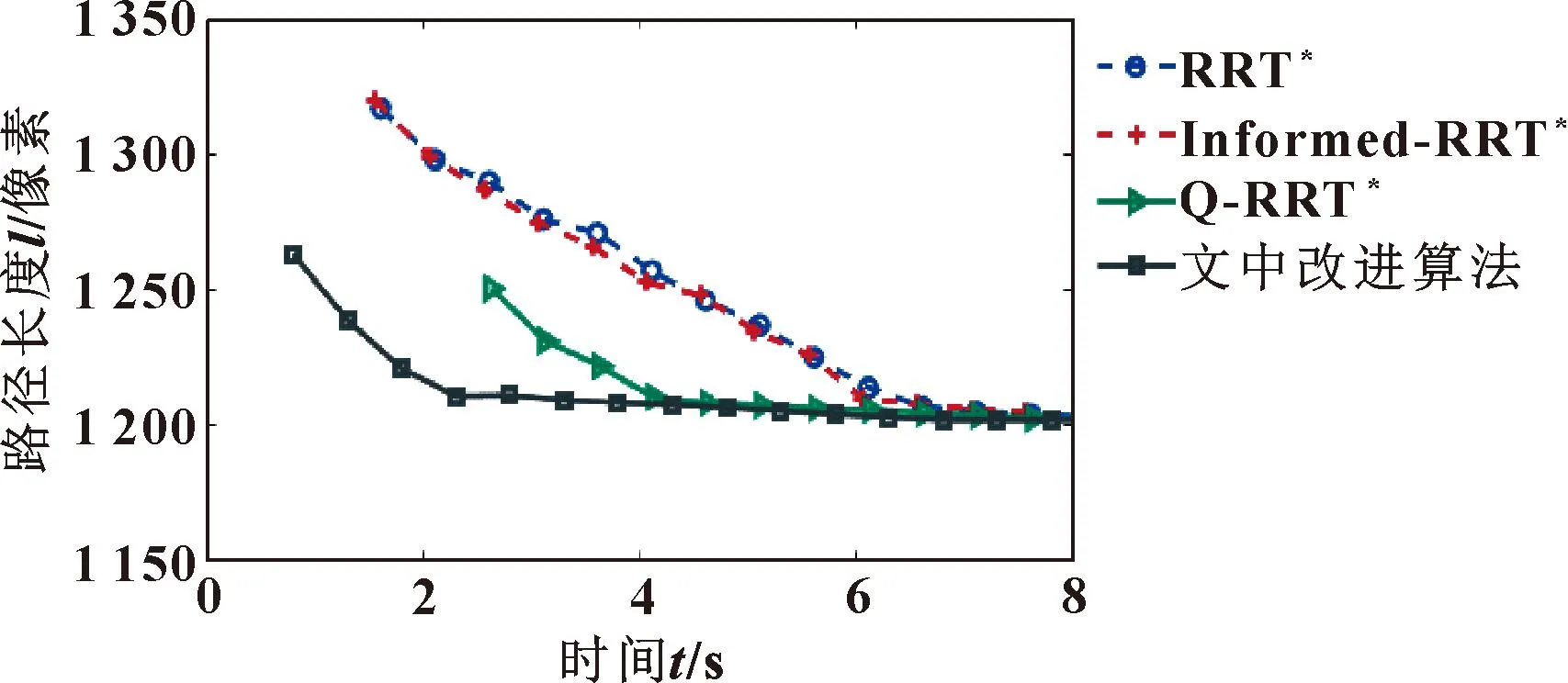

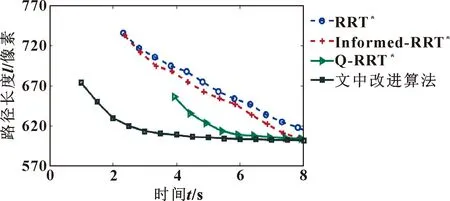
4 路径规划实验
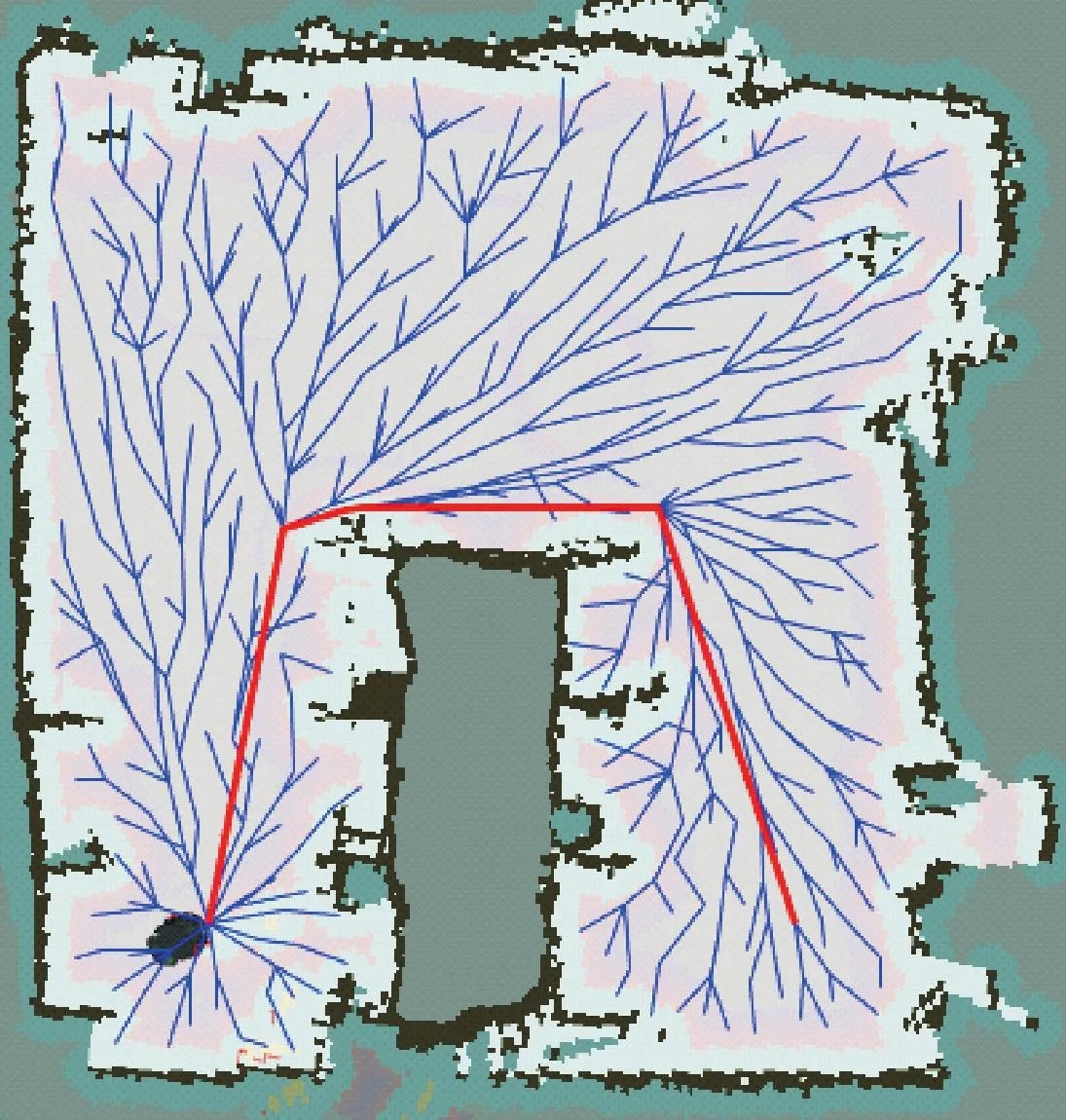

5 结论

