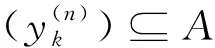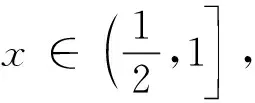对称度量空间上的一个注记
郑顶伟,洪宇翔,何庆明
(广西大学 数学与信息科学学院, 广西 南宁 530004)
0 引言
一个对称度量空间[1]指的是一个序对(X,d),其中X是一个非空集,d:X×X→[0,∞)是一个函数,使得对x,y∈X,下列条件成立:
①d(x,y)=0当且仅当x=y。
②d(x,y)=d(y,x)。
对称度量与度量空间的区别在于缺失了三角不等式。尽管如此,一些度量空间中概念可以类似地在对称度量空间中定义。在对称度量空间(X,d)中,序列(xn)的极限定义如下:
limd(xn,x)=0⟺limxn=x。
以x为中心、r为半径的开球定义如下:
B(x,r)={y∈X:d(x,y) 与度量公理比较,对称度量缺少三角不等式,从而通常的ε球B(x,ε)={y∈X:d(x,y)<ε}不能形成拓扑的基。 一个对称度量空间(X,d)称为一个半度量空间,如果满足对任意A⊂X, 所以,对一个对称度量空间(X,d),如果映射c:A→c(A)={x∈X:d(x,A)=0}是闭包运算,则(X,d)是一个半度量空间。 对称度量与半度量的区别也可以反映在序列的收敛上[2]。在半度量空间中,d(xn,x)→0和以拓扑τd意义下xn→x是等价的。而在对称度量空间中,以拓扑τd意义下xn→x是推不出d(xn,x)→0的,所以研究在什么条件下对称度量空间是半度量空间是有意义的。 定义1[1]对集合X,函数d:X×X→R+称为X的对称距离,若对x,y∈X,下述条件成立: ①d(x,y)=0当且仅当x=y。 ②d(x,y)=d(y,x)。 空间X称为对称度量空间,如果存在X的对称距离d,满足U∈τ(X)当且仅当对x∈U,存在ε>0,使B(x,ε)⊂U,这时d称为X的对称度量。 若d是X的对称距离,那么(X,d)是对称度量空间当且仅当d满足:A⊂X是X的闭集的充要条件是对x∈X-A,d(x,A)>0。易验证,对称度量性是可加性、开遗传性和闭遗传性。 定义2[1]设d是X的对称距离,d称为X的半度量,若(X,d)是对称度量空间,并且对x∈X和ε>0,x∈B(x,ε)°,这时(X,d)称为半度量空间。 设(X,d)是对称度量空间, 则有以下2种方式引入拓扑: 方式1U是开集当且仅当对任意x∈U,存在ε>0,使得B(x,ε)⊂U。按照此种方式显然生成一个拓扑,本文将这个拓扑记为τ1。 下面证明这2个拓扑是同一个拓扑,即τ2=τ1。 证明首先证明τ1⊂τ2。 任意取U∈τ1,要证U∈τ2,只需证X-U是τ2中的闭集。设x∈X,d(x,X-U)=0。下证x∈X-U。 反证法。若x∉X-U,则x∈U。由于U∈τ1,则存在ε>0,使得B(x,ε)⊂U,因此d(x,X-U)≥ε,与d(x,X-U)=0矛盾,故x∈X-U,即X-U是τ2中的闭集,则U∈τ2。τ1⊂τ2得证。 其次证明τ2⊂τ1。 设U∈τ2,则X-U是τ2中的闭集。下证U∈τ1。 反证法。若U∉τ1,则存在x∈U, 对任意ε>0, 有B(x,ε)⊄U。 同理,可以验证下面关于半度量空间的定义是相同的。 ① 一个对称度量空间(X,d)称为一个半度量空间,如果满足对任意A⊂X, ② 一个对称度量空间(X,d)称为一个半度量空间,如果满足对任意x∈X,ε>0,有x∈int(B(x,ε))。 由①可知,d(x,X-B(x,ε))=0,但显然d(x,X-B(x,ε))≥ε,矛盾。 limd(x,yn)=0即d(x,A)=0。 许多学者在对称度量空间(X,d)提出新的条件来作为三角不等式的部分替代。1931年,Wilson[3]在半度量空间上提出性质Wilson Ⅲ(以下简称W3)和性质Wilson Ⅳ[3](以下简称W4)。1993年,Czerwik[4]提出度量型(metric type:MT)性质。1995年,Jachymski等[5]提出了性质(JMS)。2003年,Aamri等[6]提出性质(HE)。2006年,Mihet[7]提出性质(W)来替换性质(W3)和(W4)。2008年,Cho等[8]提出了一个与对称度量d的连续性有关的新性质(CC)。2012年,Arandelovic等[9]提出性质(SC)。 定义3设(X,d)是一个对称度量空间。定义下列性质: (MT)[4]: 存在s≥1使得对任意x、y、z有d(x,z)≤s(d(x,y)+d(y,z))。 在文献[9]中,Arandelovic和Keckic对对称度量空间做了详尽的讨论,特别地,他们得到了下面的定理。 定理1设(X,d)是一个对称度量空间,则下列条件等价: ②(X,d)是一个半度量空间且每个B(x,r)是开集。 问题1设(X,d)是一个对称度量空间且满足性质(W4)和(HE),那么它满足性质(CC)吗? 问题2设(X,d)是一个对称度量空间且满足性质(W),那么它满足性质(CC)吗? 问题3设(X,d)是一个对称度量空间且满足度量型(metric type:MT)性质,那么它是一个半度量空间吗? MT性质的对称度量空间也被称为度量型空间或b-度量空间。许多学者讨论和研究了其上的拓扑性质以及不动点理论,获得了一系列不动点定理,可参看文献[9]及其参考文献。 引理1[9]设(X,d)是一个对称度量空间且具有MT性质,则(X,d)具有性质 (W)、(W3)、(W4)、(HE)、(W) 及(JMS)。 本文主要解决上述问题:其中肯定回答问题3,而问题1和问题2则是否定回答。 定理2设(X,d)是一个对称度量空间并且满足MT性质, 也就是说,存在s>1使得对任意x,y,z∈X,d(x,z)≤s(d(x,y)+d(y,z)), 则(X,d)是一个半度量空间。 d(x,A)=inf{d(x,a):a∈A}。 为了证明(X,d)是一个半度量空间,本文只需要验证映射c是拓扑τd中的闭包运算,其中 c:A→c(A)={x∈X:d(x,A)=0}。 首先,证明若A⊂X是一个闭集,则c(A)=A。 因为c(A)⊇A恒成立,所以只需要证明相反的包含关系c(A)⊆A。对x∈c(A),则d(x,A)=0,由于A是τd中的闭集,由拓扑的定义知x∈A,即c(A)⊆A,从而可证c(A)=A。 其次,证明对任意一个非空集A⊂X,c(A) 是τd中的闭集。 设x∈X使得d(x,c(A))=0, 则存在序列(xn)⊆c(A) 使得 (1) (2) 由MT性质,得 (3) 那么由式(1)-(3),可得 (4) 最后,容易看出,若B是闭集且B⊇A, 则B⊇c(A)。 从以上证明可以看出,c(A)是包含A的最小闭集,从而说明映射c是拓扑τd中的闭包运算,其中c:A→c(A)={x∈X:d(x,A)=0},也就是说(X,d)是一个半度量空间。 由定理2,本文可正面回答问题3。基于定理1、引理1和文献[9]中的一个例子,给出问题1与问题2否定回答。顺便提一下问题2已由Shahzad等在文献[10]中解决。 例1设δ>0,X=[0,1]∪{2}赋予欧氏距离d。定义d*如下: 则对x,y,z∈X,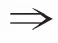

1 预备知识
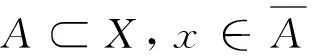
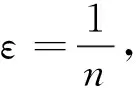
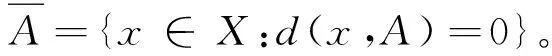
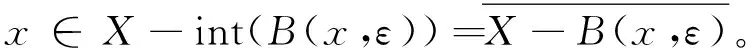
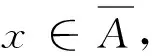
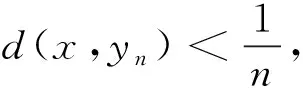
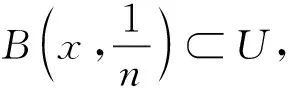

2 主要结果