用对数均值不等式求解高考导数压轴题
——以近五年高考导数压轴题为例
焦永垚
(甘肃省兰州市第六中学)
1.提出问题
导数及其应用是历年高考的重要考点之一,其中含ex,lnx的函数零点、函数极值、数列不等式及极值点偏移等问题成为近年高考的热门考点,在全国各地高考压轴题中频繁出现,对数均值不等式是解决此类问题的一个有力工具.很多学生只是简单记住了对数均值不等式的形式,但具体在什么情况下使用,怎么使用,往往比较困惑,加之导数压轴题具有综合性强、计算量大、思维要求高等特点,致使学生对导数压轴题望而生畏,不敢下笔.本文以近年高考试卷中的导数压轴题为例,阐述对数均值不等式及其推论在解题中的应用,以期抛砖引玉.
2.对数均值不等式及其推论
两个正数a,b的对数平均定义如下:
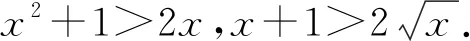
对数均值不等式的证明方法很多,以上采用定积分函数放缩的高观点视角证明,可以帮助学生高位审视问题,有助于学生思维方式的训练和认知的提升.另外,由对数均值不等式很容易得到以下三个推论:
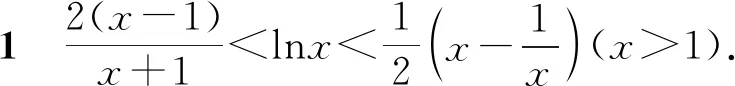
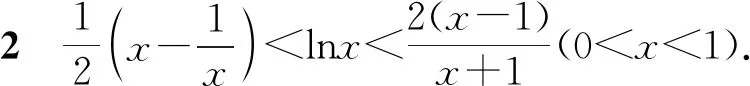
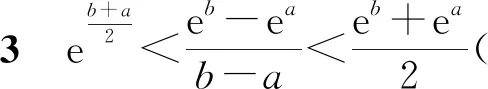
3.对数均值不等式及其推论在高考导数压轴题中的应用
3.1 解决数列不等式的证明问题
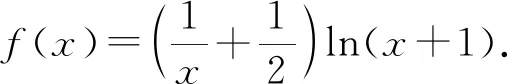
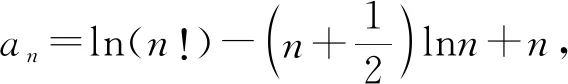
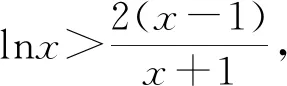
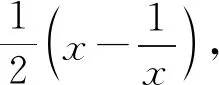
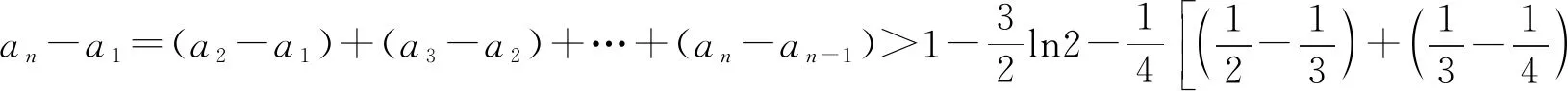
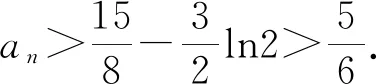
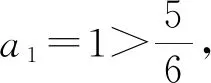
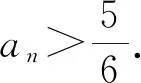

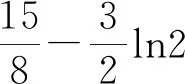
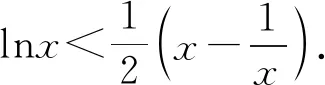

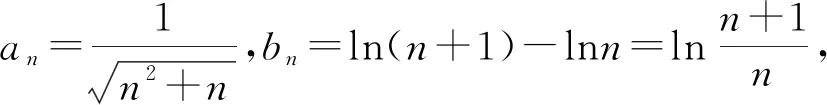


3.2 解决函数不等式的证明问题
【例3】(2020·天津卷·20节选)已知函数f(x)=x3+klnx(k∈R),f′(x)为f(x)的导函数.

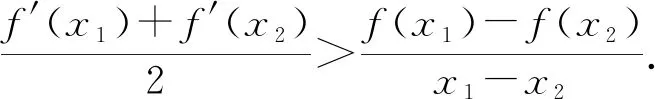
【解析】(Ⅰ)函数g(x)的单调增区间为(1,+∞),单调减区间为(0,1),极小值为g(1)=1,无极大值.(过程略)




【评注】此题通过换元,利用对数均值不等式的推论1将(x1-x2)[f′(x1)+f′(x2)]-2[f(x1)-f(x2)]进行放缩,从而成功把要证的不等式与第(Ⅰ)问中的函数g(x)相联系,再借第(Ⅰ)问的结论进行解决,极大降低了思维难度.
3.3 解决函数的极值或零点问题


当a≤0时,g′(x)>0,g(x)在(0,+∞)上单调递增,则g(x)>g(0)=0,从而g(x)在(0,+∞)内没有零点.

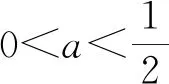
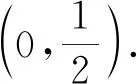

【例5】(2020·浙江卷·22节选)已知1 【解析】因为当x∈(0,+∞)时,f′(x)=ex-1>0,所以f(x)在(0,+∞)上单调递增,且f(x0)=ex0-x0-a=0,其中x0∈(0,+∞). 要证不等式x0f(ex0)≥(e-1)(a-1)a成立,则只需证ax0(ex0-1)>(e-1)(a-1)a,即证x0(ex0-1)>(e-1)(ex0-x0-1).令g(x)=x(ex-1)-(e-1)(ex-x-1)(x>0),则g′(x)=(x+2-e)ex+e-2,设h(x)=g′(x),则h′(x)=(x+3-e)ex>0,所以g′(x)在(0,+∞)上单调递增,可得g′(x)>g′(0)=0,所以g(x)在(0,+∞)上单调递增,得g(x)>g(0)=0,则g(x0)>0,从而x0(ex0-1)>(e-1)(ex0-x0-1),故原不等式成立. (Ⅰ)若f(x)≥0,求a的取值范围; (Ⅱ)证明:若f(x)有两个零点x1,x2,则x1x2<1. 【解析】(Ⅰ)实数a的取值范围是(-∞,e+1].(过程略) 【例7】(2021·新高考Ⅰ卷·22)已知函数f(x)=x(1-lnx). (Ⅰ)讨论f(x)的单调性; 【解析】(Ⅰ)f(x)在(0,1)上单调递增,在(1,+∞)上单调递减.(过程略) 综上所述,2 【评注】对于极值点偏移问题,常规的解决方法是构造对称函数,但上述例6先根据f(x1)=f(x2)建立关于x1,x2的等式,再通过同构、恒等变形等将其转化为对数平均,再利用对数均值不等式解决,思路简单自然,抓住了问题的本质.例7在证明“x1+x2>2”时,借助对数均值不等式的推论把含lnx1,lnx2的超越式放缩为有理式,从而使问题迎刃而解.高考中的极值点偏移问题还有很多,如2016年全国Ⅰ卷理科第21题、2013年湖南卷文科第21题、2010年天津卷理科第21题等等,有兴趣的读者可尝试运用对数均值不等式及其推论进行解决,本文不再赘述. 从历年的高考试题可以看出,以对数均值不等式及其推论为背景的高考题屡见不鲜.虽然对数均值不等式在高中数学教材中没有专门介绍,但是理解和掌握对数均值不等式及其应用,能够帮助学生快速明确解题方向,这对学生突破导数压轴题有着至关重要的作用.对数均值不等式其实是学生所熟知的基本不等式的加强,其几何意义是以罗尔中值定理为背景,属于高等数学知识,因此,在实际解题过程中,凡涉及使用对数均值不等式的,都需先给出证明.近年来,很多高考试题的命制都以高等数学中的部分思想与内容为背景,因此,作为一名高中数学教师,仅仅具备高中数学教材中的知识是远远不够的,在教学中还要注重渗透“高观点”思想,教会学生善于从“高观点”去审视和解决数学问题,这可使学生能够更好地理解和把握命题意图,更有利于提升学生的思想高度,更有利于培育学生的思维创新能力,更有利于发展学生的数学核心素养.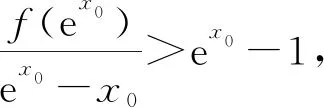
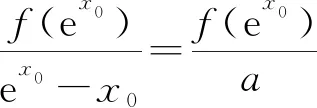

3.4 解决极值点偏移问题

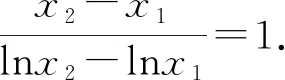
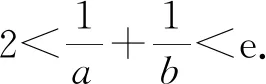
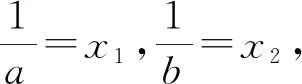

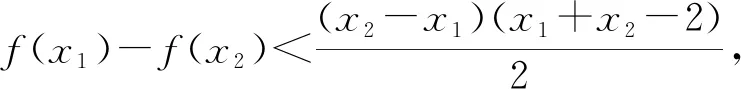
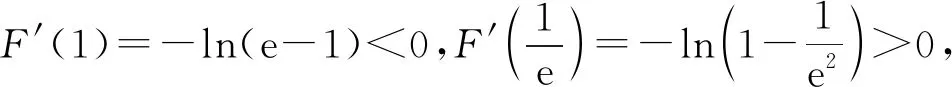

4.结束语

