水平轴风力机气动转矩模型优化研究

张 琳, 刘旭东, 常佳飞, 艾 超, 陈立娟, 陈文婷

(1.燕山大学 河北省重型机械流体动力传输与控制实验室, 河北 秦皇岛 066004;2.南京工程学院 机械工程学院, 江苏 南京 211167)

引言

风能因其储量丰富、绿色环保等特点已成为全球新能源领域的重点发展对象[1-2]。风力机是风电机组捕获风能,实现能量转换的关键部件。不考虑偏航、调桨等人为可调因素对风力机的影响,风力机叶片的材质成为了建立风力机气动转矩模型和对机组并网发电控制性能评估的关键。同时自然风的随机性使风力机叶片的气动载荷复杂且多变,故获取风力机的输出特性规律和气动转矩的精准模型对提升风力机性能和控制机组发电至关重要。

风电机组的控制性能提升受风力机运行特性和模型精度的制约,而风力机的叶片材质、结构参数均会对风力机运行特性造成影响。现阶段对风力机运行特性的研究主要集中在其材质和结构特性等方面。OZDAMAR G等[3]研究了风力机叶片材料对风力机效率的影响。张嘉奇等[4]研究了材质对风力机叶片绕流流场的影响。郑玉巧等[5]揭示了叶片不同铺层材料单层厚度对模态频率的影响规律。冯博琳等[6]分析了不同风速下叶片表面压力、叶片应力分布及形变之间的关系。ROUL R等[7]探究了桨距角对水平轴风力机气动特性和结构特性的影响。TIAN K等[8]对风力机叶片上的气动载荷分布进行了数值模拟,并计算了叶片应力。包道日娜等[9]基于水平轴可变偏心距风力机,分析了不同工况下可变偏心距风力机输出特性的变化规律。刘东等[10]分析了5 kW伞形风力机风轮收缩角对风力机尾流及功率输出特性的影响。郭少真等[11]以NACA0012翼型叶片为例,探究了径长比对最大输出功率的影响。方玉财等[12]分析了叶片非振动与施加弯矩后风轮输出特性变化。上述研究成果对风力机叶片的设计优化和性能评估均有重要意义。而现有研究中对风电机组的风力机气动转矩模型研究较少,常见的水平轴风力机气动转矩模型在研究时存在无法完全考虑各因素影响、依赖叶片效率因子等参数化方法、试验数据具有不确定性以及模型建立与验证仅单一依赖仿真或试验数据等问题[13-15],且其模型准确性和修正过程鲜有研究。

因此,亟需从风电机组控制性能提升出发,研究风力机的材质对输出特性的影响,并通过大量实验数据与模拟仿真相结合,揭示风力机输出特性规律,优化风力机气动转矩模型的构建过程,实现气动转矩模型的精准建模,进而为风电机组的并网发电控制提供精准的控制指令。

1 风力机模型的建立

1.1 风力机三维模型预处理

本研究根据青岛某风电企业所提供的AH-30 kW变桨距风力发电机的叶片三维模型进行研究,其参数如表1所示。

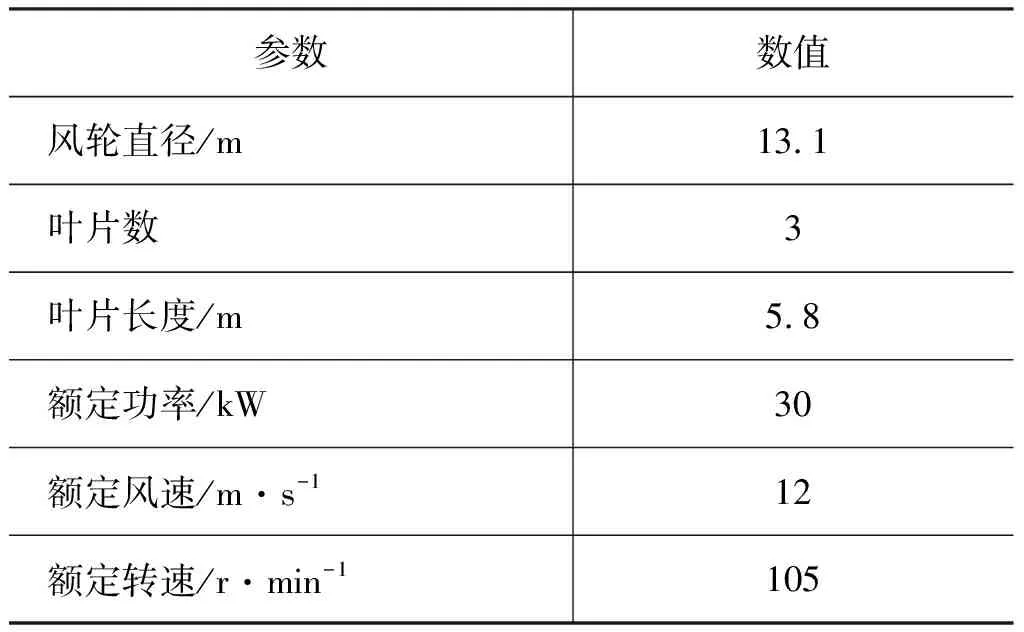
表1 风力机叶片参数Tab.1 Wind turbine blade parameters

为了提高网格划分质量和仿真计算的收敛精度,对叶片边缘较薄的地方进行优化。同时轮毂部分不作为重点分析对象,对其也进行优化处理。优化前后的模型如图1所示。

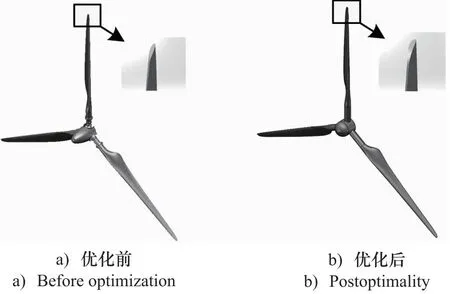
图1 风力机三维模型

1.2 风力机数学模型的建立

本研究选用风力机的简化模型,假设叶片表现为翼型且为刚性叶片,其气动转矩和捕获的风功率数学模型可表示为[16]：

(1)

(2)

式中,Tw—— 风力机输出转矩

ωw—— 风力机转速

Pw—— 捕获的风功率

Cp—— 风能利用系数

ρ—— 空气密度

R—— 叶片半径

β—— 叶片桨距角

λ—— 叶尖速比系数

v—— 有效风速

α—— 风力机修正系数

风能利用系数Cp(λ,β)表示为[17-18]：

(3)

(4)

其中,系数C1=0.5176,C2=116,C3=0.4,C4=5,C5=21,C6=0.0068。

叶尖速比λ可表示为：

(5)

1.3 风力机流场模型的建立

为了更好的研究风力机的叶片材质对机组运行特性及气动转矩输出特性的影响,通过ANSYS有限元分析软件对风力机进行流固耦合分析。由于风轮旋转时周围流场范围无穷大,但在仿真时无法模拟无穷大的流场,因此对其周围的流场范围进行划定。考虑到叶片旋转会对叶片周围的气流产生作用,因此将叶片外的流域划分为两部分,即内流域和外流域。内流域为圆柱形的旋转域,其内部挖掉风力机外形的型腔,在风机旋转过程中随着风机叶片的转动而同轴旋转,与风力机保持相对静止状态。外流域为圆柱形的静止域,其包裹在旋转域外面,在内流域旋转时保持静止。其流域如图2所示。

图2 风场流域划分图

利用ANSYS Workbench中的Mesh模块对流体域网格进行划分,因流体计算对网格的划分要求较高,因此需要对流体域中较为复杂的部分进行局部网格加密,其中流体网格划分如图3所示。划分后网格节点为531009,网格单元为2915626,选取网格度量标准为单元质量,网格单元质量最小值达到了0.2且平均值达到了0.8,满足质量要求,且在后续进行仿真初始化时收敛公差达到了10-6,满足网格品质基本需求。

图3 流体域网格划分图

对风力机流固耦合的边界条件设置如图4所示,设定内流域随风轮一起旋转,旋转速度为实际风轮转速,外流域为风轮所处的外界环境,设置其为静止,入口边界类型为速度边界,其大小设置为实际风速,出口边界为压力边界,相对值设为0,叶片边界设置为壁面,且与内流域同转速旋转。

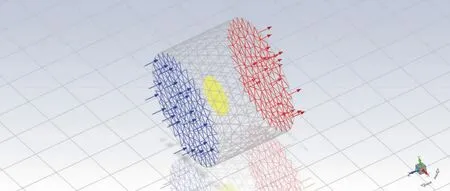
图4 边界条件设置模型图

1.4 网格无关性分析

采用加密边界层和未加密边界层两种网格数量控制方法划分网格,分析加密边界层对计算结果的影响,加密前后的扇叶力矩如图5所示。对比发现,加密边界层控制网格数量的方法对数值模拟结果的精度有着略微的提升,即加密边界层能使数值模拟结果的计算精度提高。

图5 网格加密前后扇叶力矩图

对流体域划分不同数量的网格进行数值模拟,将计算的力矩值与实验数据对比可知,当流体域的网格数量达到291万后,对力矩的计算结果没有太大影响,因此可以认定流体域划分的网格数量达到291万时满足网格无关性要求。

2 风力机叶片材质影响分析

利用Fluent对风力机载荷进行分析,其过程为稳态过程,重力加速度选择Y轴方向-9.8 m/s2,湍流模型选择SST湍流模型,求解器选择SIMPLE算法,残差设定为10-3,迭代步数设置为1500,同时设定入口速度为风力机额定风速12 m/s,设定内流域为参考系运动,风力机额定转速设为105 r/min,设置完成后对其进行求解计算。

为了研究风力机叶片材质对风力机运行特性的影响,考虑所研究对象实际材料为单一材质,因此不对多材料铺层复合材质进行研究。重点关注典型材质风力机叶片在额定工况下应力及变形情况,3种典型材料具体参数如表2所示,求解结果如图6～图8所示,为了使结果更容易观察分析,对风力机形变的效果进行了2倍放大,同时将各材料的相关结果参数汇总于表3。

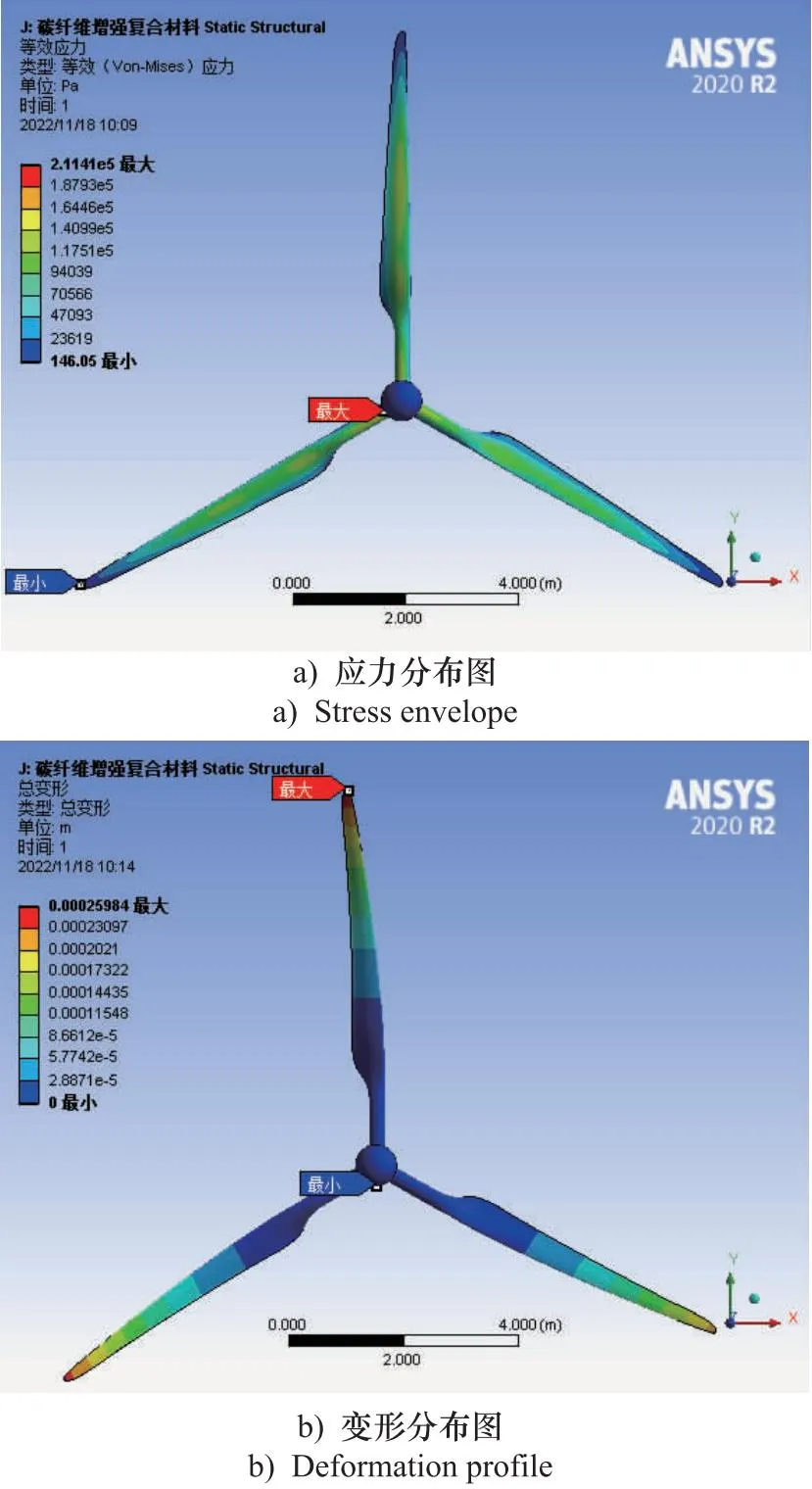
图6 碳纤维增强复合材料结果图

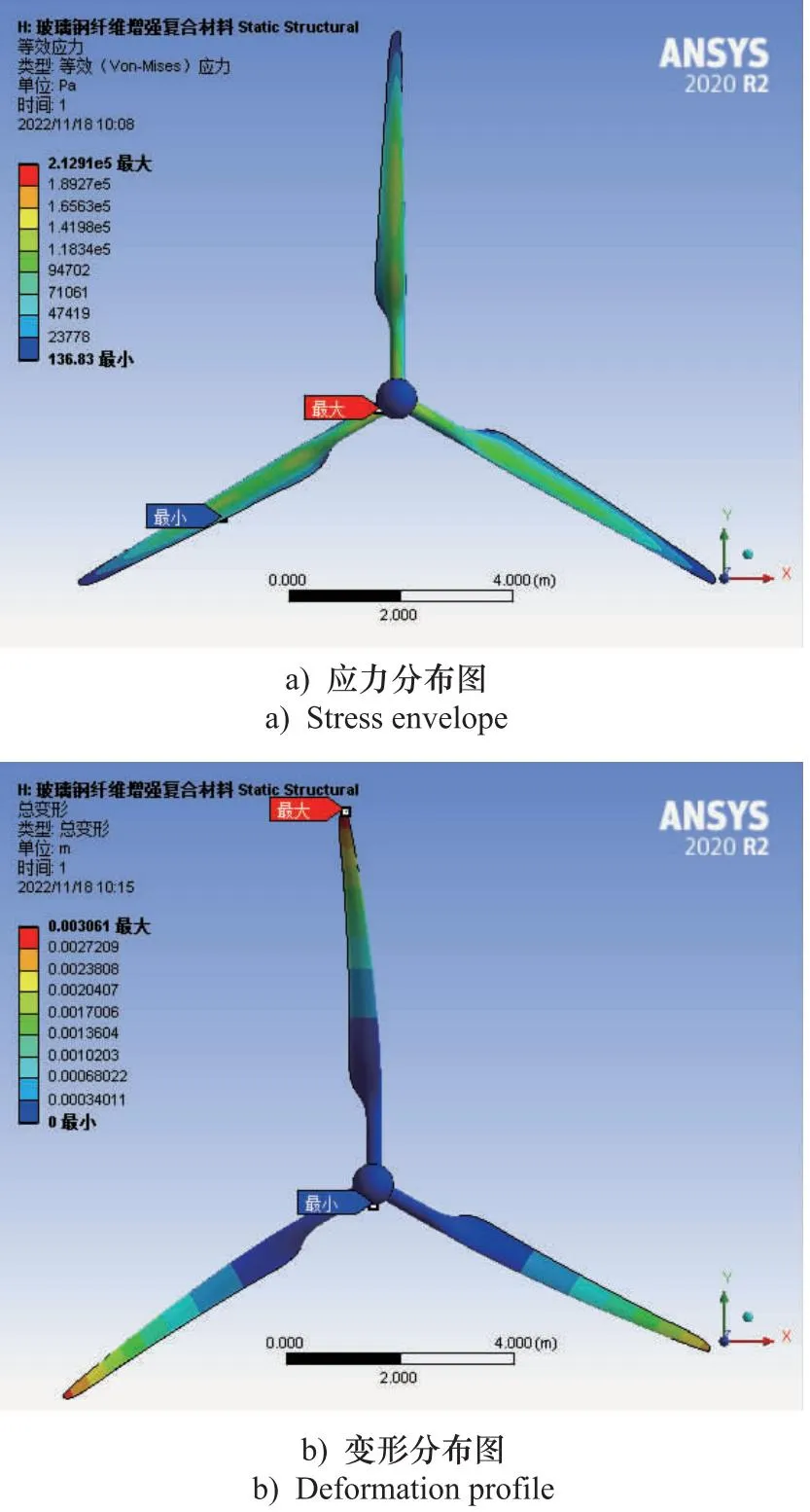
图7 玻璃钢纤维增强复合材料结果图

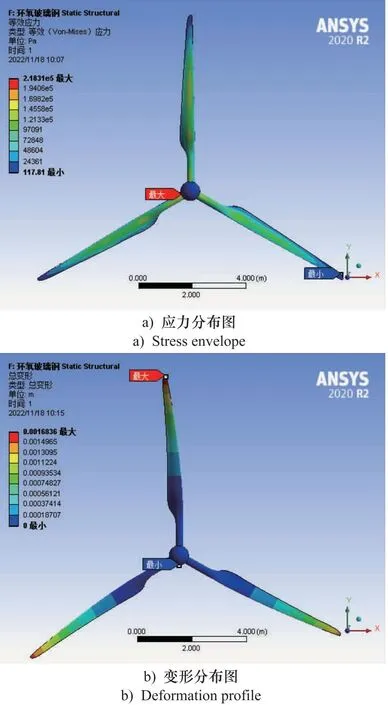
图8 环氧玻璃钢结果图

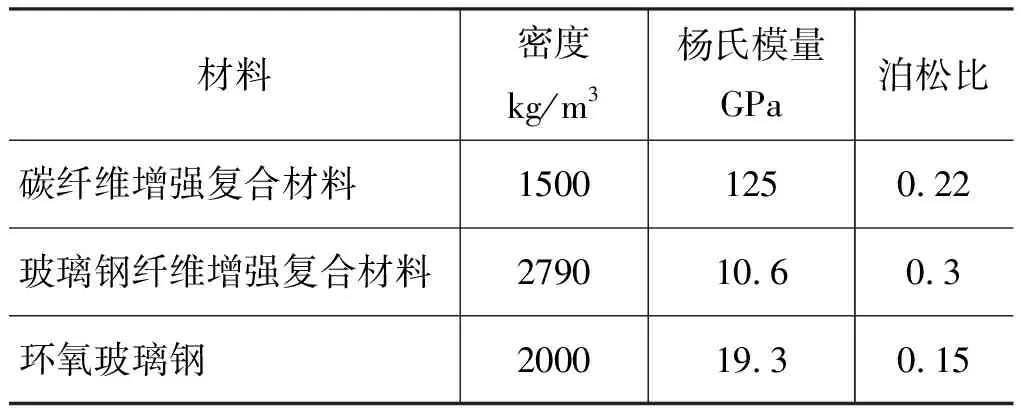
表2 常用叶片材料参数表[19-21]Tab.2 Table of commonly used blade material parameters

表3 常用叶片材料结果表Tab.3 Table of results for commonly used leaf materials

由图6～图8及表3结果可知,3种材料叶片所受应力大致相同,在形变方面,叶片上的变形主要集中在叶片尖端部分,且3种材料在额定工况下的形变程度相差较大,但整体形变量较小,故风机受材质不同而产生的形变,对风力机转矩模型和机组控制影响可忽略不计。

3 风力机气动转矩输出特性分析

利用Fluent对风力机输出转矩进行分析,其过程为瞬态过程,重力加速度选择Y轴方向-9.8 m/s2,湍流模型选择SST湍流模型,求解器选择PISO算法,残差设定为10-3,时间步长选取0.1,时长数量选取1200,最大迭代步数设置为200。

3.1 实测风速下风力机输出转矩分析

为进行风力机输出特性分析,选定材质为环氧玻璃钢的风力机叶片,根据合作厂商提供的现场实测数据对风速和风力机转速进行设定。根据实测数据,选取不同时间段的两组数据,每组数据选取120 s,由于受设备限制,实测数据采样周期为10 s,采样频率较低,因此根据采样数据的特点对其进行多项式拟合,以便于仿真计算求解。

对第1组和第2组数据的风速和风轮转速进行曲线拟合,此处根据数据的分布选取五项式进行拟合,拟合公式如式(6)所示,拟合参数如表4和表5所示。

y=Intercept+B1t+B2t2+B3t3+B4t4+B5t5+B6t6

(6)

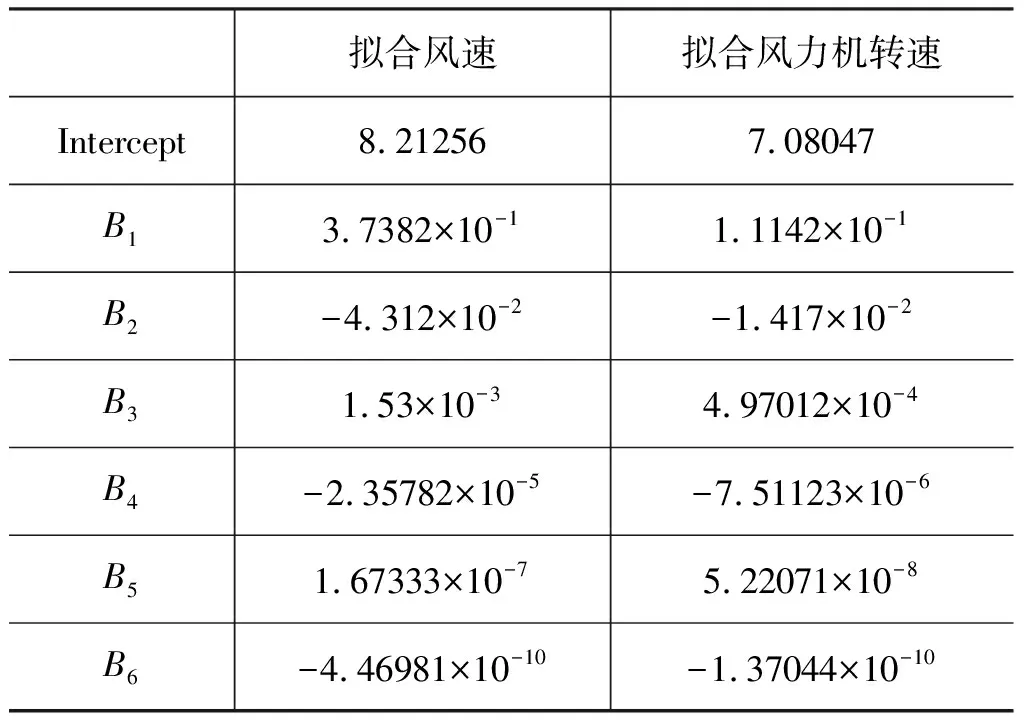
表4 工况1中风速风轮转速拟合参数表Tab.4 Table of fitting parameters of wind speed and wind wheel speed in working condition 1

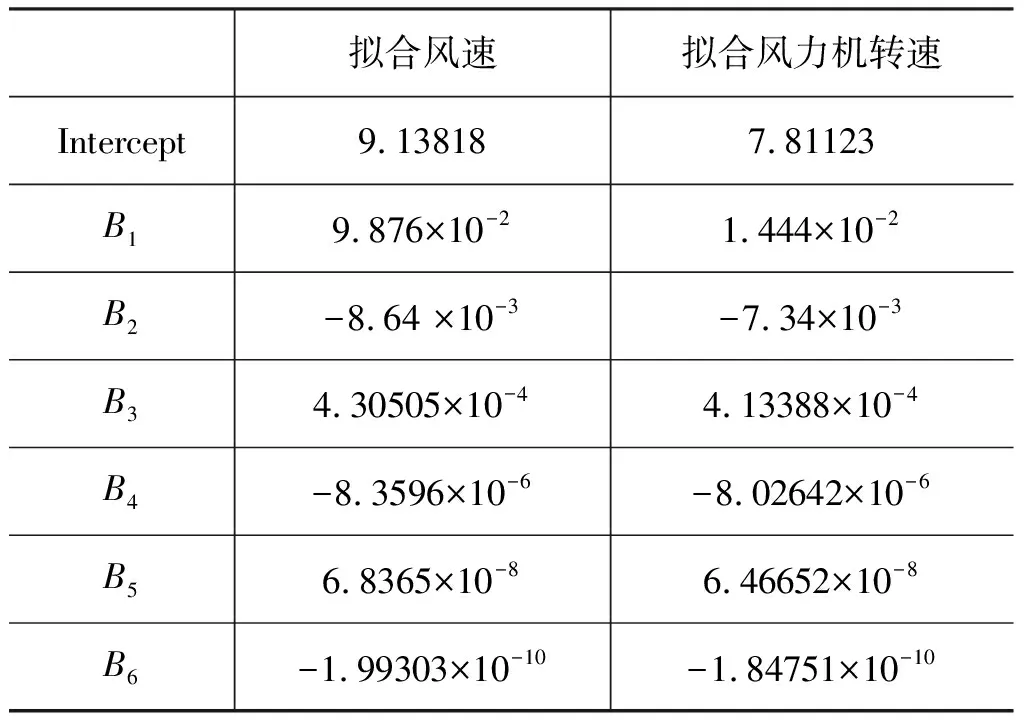
表5 工况2中风速风轮转速拟合参数表Tab.5 Table of fitting parameters of wind speed and wind wheel speed in working condition 2

其拟合后曲线如图9、图10所示。

图9 工况1拟合曲线

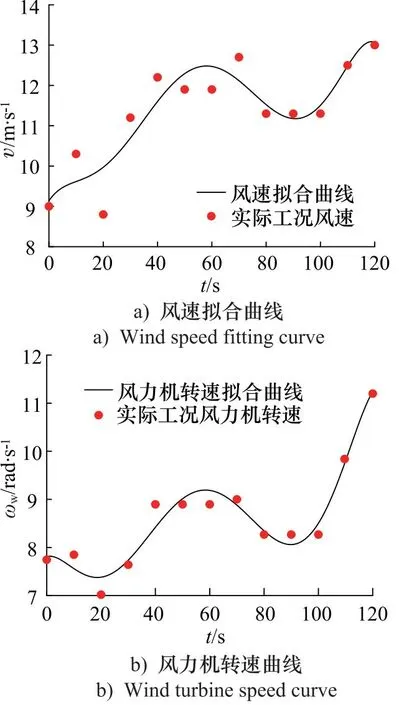
图10 工况2拟合曲线

将上述两组拟合公式分别在Fluent中编写成各自的wind和rotor表达式,并设置风速的边界条件为wind,设置内流域为网格运动,旋转速度为rotor,并进行初始化,基于已完成的求解器设置,对模型进行计算。

同时为了进一步验证仿真计算结果的准确性,考虑到实测数据无法采集风轮的输出转矩和输出功率,因此间接根据风力机发电的功率与风轮转速比值的变化趋势反向验证计算结果的准确性,具体对比如图11、图12所示。

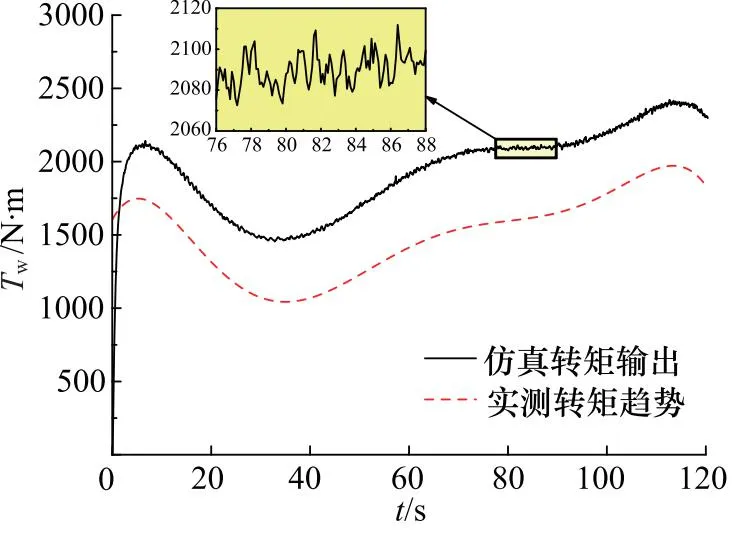
图11 工况1风力机转矩输出曲线

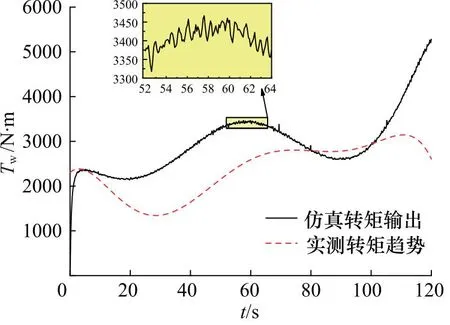
图12 工况2风力机转矩输出曲线

通过两组工况下的输出曲线结果可知,利用Fluent仿真所计算结果和实测风力机发电的功率与风轮转速比值变化趋势基本一致。但是风力机与发电机之间能量传输过程存在传动效率、储能部分能量储放导致的能量损失及反向验证方法计算不够准确等,因此误差在所难免。而工况2中误差较大的原因在于此时间段内储能环节处于工作状态且曲线拟合存在误差较大等。

通过两个工况的转矩输出结果进一步分析可知,风力机输出转矩在受自然风影响发生大幅度波动的同时,其也存在一定的抖颤,这与风力机自身的结构和机组部分参数时变相关,因此,在对风力机输出的能量进行控制利用时,不仅要充分考虑外界扰动的影响,也需要关注机组内部存在的扰动。

3.2 风力机数学模型修正

根据建立的风力机数学模型,式(2)中的风力机修正系数受风电机组的额定功率影响,故需根据实际情况进行修正。本研究根据实际风速、风力机转速下所仿真得到的输出转矩对所建立的风力机数学模型进行修正。

将两组工况下所拟合的风速曲线和风力机转速曲线输入到所建立的式(2)中,并先设置风力机修正系数为1,利用该数学模型计算得到两组工况的风力机输出转矩,将其与Fluent仿真出的风力机输出转矩进行对比如图13、图14所示。

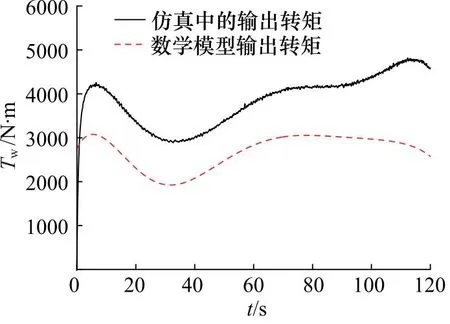
图13 工况1风力机转矩输出对比曲线

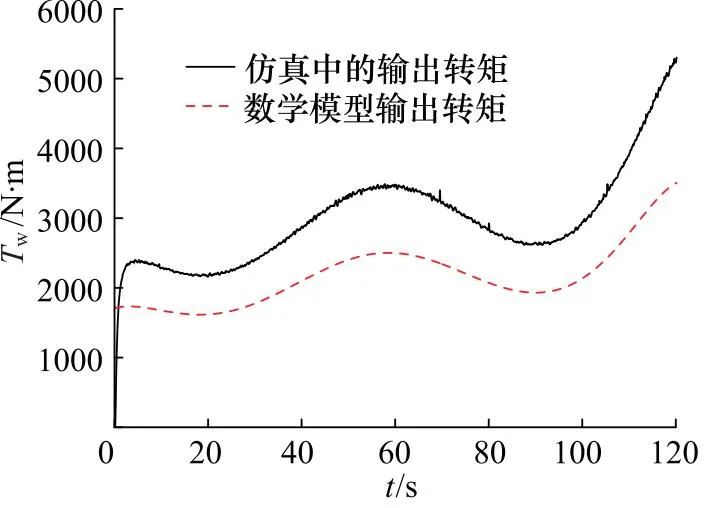
图14 工况2风力机转矩输出对比曲线

通过图13、图14可知,根据风力机数学模型计算的输出转矩与Fluent仿真中的输出转矩变化趋势一致,再次验证利用Fluent仿真计算结果的可靠性。而5 s之前由于Fluent软件仿真时,风速和风力机转速初始化后存在响应过程,因此可以忽略不计。对两组工况去掉前5 s的数据进行分析计算,并取所有数据的平均值可得风力机修正系数α=1.455。

为了进一步验证风力机修正系数的准确度,另选一组风速和风力机转速,并根据数据分布特点选取八项式对其进行拟合,其拟合公式如式(7),拟合参数如表6。

表6 工况3中风速风轮转速拟合参数表Tab.6 Table of fitting parameters of wind speed and wind wheel speed in working condition three

y=Intercept+B1t+B2t2+B3t3+B4t4+B5t5+B6t6+B7t7+B8t8

(7)

其拟合后曲线如图15所示。将风速和风力机转速拟合公式分别设置为边界条件,对其进行计算,同时将两组拟合曲线代入到修正后的风力机数学模型中,得到修正后风力机数学模型的输出转矩曲线,其对比如图16所示。

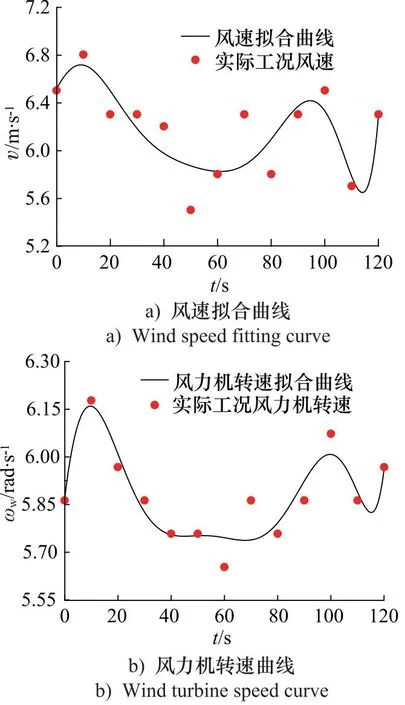
图15 工况3拟合曲线

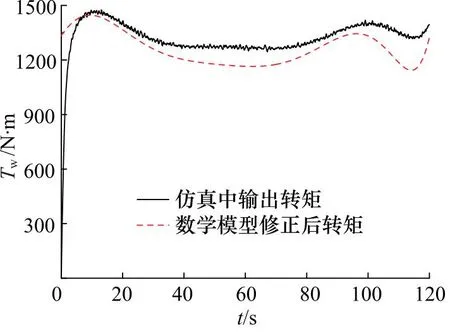
图16 工况3风力机转矩输出对比曲线

根据上述曲线可知,修正后的风力机气动转数学模型与Fluent仿真中的输出转矩较为吻合,通过计算可知其误差为5.60%,修正后的模型在误差允许范围之内,故修正后的风力机数学模型能够较好的反映真实风力机输出特性。且由于利用实测数据与数值模拟相结合的方式对数学模型修订时,改变的仅是风力机计算模型的系数,并未对公式原理进行改变,因此,该方法同样适用于其他型号风力机叶片。修正后模型存在的误差可能来源于风力机三维模型的优化处理、风速和风力机转速曲线拟合时与实测数据之间的误差、风力机网格划分精度、求解器的设置以及风力机叶片微小的变形等。

4 结论

(1) 以AH-30 kW变桨距风力发电机的叶片为研究对象,在额定工况下对碳纤维增强复合材料、玻璃钢纤维增强复合材料和环氧玻璃钢3种典型叶片材质的风力机进行了应力、形变分析,并发现中小型风力机叶片受材质不同而产生的形变均为细微形变,故不同材质叶片产生的形变差异在对风力机气动转矩建模和对机组控制时可以忽略;

(2) 针对环氧玻璃钢材质的风力机叶片,利用实测风速和风力机转速数据设置Fluent仿真的边界条件进行风力机输出转矩仿真分析,仿真计算结果和实测风力机发电的功率与风轮转速比值变化趋势基本一致;此外,风力机输出转矩受风速影响存在较大波动的同时,自身也存在一定的抖颤,故在对风力机输出能量控制利用时,在充分考虑外界扰动时,也需要对机组所存在的内部扰动进行考虑;

(3) 基于实测数据和仿真模拟相结合的方式对风力机气动转矩数学模型进行了修订,修正后的风力机气动转数学模型与Fluent仿真的输出转矩误差为5.60%,故修正后的风力机数学模型能够较好的反映真实风力机输出特性,为风电机组的精准控制提供了精准的指令模型。