SPA-HRDE在机械设备声信号故障诊断中的应用
刘儒林, 汪 进, 谢忠志
(1.浙江工业大学 机械工程学院, 浙江 杭州 310014; 2.重庆开放大学 重庆工商职业学院, 重庆 400052;3.江苏电子信息职业学院 数字装备学院, 江苏 淮安 223003; 4.泰州职业技术学院 智能制造学院, 江苏 泰州 225300)
引言
机械工业的发展是制造业进步的前提,而建立完善和有效的机械设备状态监测系统能够进一步促进制造业良性发展。轴承、齿轮等零部件作为常见的机械设备,在运行中难免出现故障,研究机械的故障监测和诊断具有较大意义[1-2]。
基于声信号的故障诊断由于不用与设备接触使得其不会对设备产生负面影响,具有较好的应用前景[3]。然而由于噪声、摩擦等因素的影响导致声信号具有非线性、非平稳特点,信号的故障信息嵌入和耦合在噪声分量中。因此,需要采用信号分解方法对信号进行预处理。常见的有小波变换(Wavelet Transform,WT)、经验模态分解(Empirical Mode Decomposition,EMD)和变分模态分解(Variational Mode Decomposition,VMD)等。WANG Fei等[4]将WT与神经网络相结合,实现了液压泵的状态检测;但WT受到尺度参数和位移参数的影响,对参数敏感。付大鹏[5]和张婕等[6]分别将EMD和VMD用于滚动轴承的故障诊断,分离了振动信号中的噪声和故障成分;但是EMD和VMD存在分量选择问题,分量过多会产生信息冗余,过少则无法完整描述信号的固有特性[7]。
平滑先验分析(Smooth Prior Analysis,SPA)通过将信号分解为趋势项和去趋势项,避免了EMD和VMD的分量选择问题,而且SPA仅有单个参数,只需设置单个参数[8]。戴洪德等[9]将SPA和排列熵相结合,用于提取滚动轴承的故障特征,证明了SPA方法的有效性。葛红平等[10]利用SPA对轴承振动信号进行分解,并提取趋势项和去趋势项的散布熵,基于GK聚类实现了故障的精确识别。
基于此,使用SPA对机械设备声信号进行分解,分离信号中不同尺度的分量。声信号为非线性非平稳的复杂序列,经典的线性分析方法对此不适用。因此,许多非线性分析方法应运而生,如散布熵(Dispersion Entropy,DE)、样本熵、模糊熵和排列熵等。但上述指标都只是从单个尺度表达信号的故障特性,不能全面和完整地表征信号的复杂特征[11-13]。
学者们提出了多尺度分析方法,利用粗粒化处理将熵相结合,能够从信号中提取出多个熵值,从不同尺度反映信号的固有特性。在多尺度指标中,多尺度熵(Multiscale Sample Entropy,MSE)、多尺度模糊熵(Multiscale Fuzzy Entropy,MFE)和多尺度排列熵(Multiscale Permutation Entropy,MPE)应用最为广泛。但是MSE计算复杂,且计算短信号时易出现未定义值;MFE虽然减小了未定义值出现的概率,但对参数非常敏感。MPE忽视了信号幅值之间的相对关系[14]。
散布熵(Dispersion Entropy,DE)是ROSTAGHI M等[15]于2016年开发的一种复杂度测量熵值方法,通过正态分布函数对时间序列进行处理,引入了幅值信息,不仅具有较高的计算效率而且能够准确的量化频率和幅值的变化。ZHANG Yidong 等[16]将多尺度散布熵(Multiscale Distribution Entropy,MDE)用于滚动轴承的故障表征,准确识别了轴承的故障类型。但是该方法仅提取了信号的低频成分,未考虑高频故障特征。为捕捉信号高频分量中的信息,柯赟等[17]提出了层次散布熵(Hierarchical Dispersion Entropy,HDE),并用于喷油器的故障诊断,相较于MDE,HDE同时提取信号低频和高频分量的信息,能全面反映信号本质;但是该方法未考虑时间序列中更深层的信息。LI Yuxing等[18]为提高DE的特征表达能力,提出了反向散布熵(Reverse Dispersion Entropy,RDE),船舶噪声的识别结果验证了其优越性,但未从多个尺度进行分析,不够全面。
在模式识别方面,故障诊断的特征样本一般为小样本和非线性,支持向量机(Support Vector Machine,SVM)非常适合对其进行分析,然而SVM存在参数优化的问题[19]。
针对上述问题,采用层次反向散布熵(Hierarchical Reverse Dispersion Entropy,HRDE)改进MDE无法提取信号高频信息和HDE特征提取性能不足的缺陷,同时采用最近提出的具有良好全局优化性能的蜜獾算法(Honey Badger Algorithm,HBA)对SVM的参数进行优化,提出了一种基于SPA-HRDE和HBA-SVM的机械设备故障诊断方法。首先,使用SPA对声信号进行分解,实现趋势项和去趋势项的分离;然后,利用HRDE方法捕捉趋势项和去趋势项的特征值,得到故障特征;最后,将特征输入至HBA-SVM分类器中,进行故障的识别。
1 算法描述
1.1 平滑先验分析
SPA算法的理论[20]如下:
(1) 假定分析信号为Z,趋势分量设为Zt,构建趋势分量的线性测量模型:
Zt=Hθ+v
(1)
式中,H—— 测量矩阵
θ—— 回归系数
v—— 测量误差
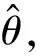
(2)
式中,λ—— 正则化系数
Dd——d阶微分算子的离散表达
(3) 假定Z有N个局部极值点,也就是:
Ze=[Z1,Z2,…,ZN]
(3)
则其一阶和二阶趋势的离散表达分别如下:
Ze1=[Z2-Z1,Z3-Z2,…,ZN-ZN-1]
(4)
Ze2=[Z3-2Z2+Z1,Z4-2Z3+Z2,…,
ZN-2ZN-1+ZN-2]
(5)
(4) 通过理论推导,可得Dd为:
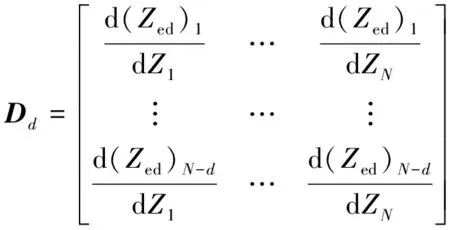
(6)
式中,Zed为Ze的第d阶趋势的离散表达,让微分项Dd(Hθ)趋近0,则式(2)表示如下:
(7)
(8)
(5) 为约简趋势分量的求解,假定H为单位矩阵,Dd设为2阶,如下:
(9)
(10)
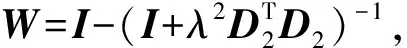
1.2 层次反向散布熵特征提取
1) 反向散布熵
反向散布熵是反映时间序列动态特性的非线性动力学方法,性能优于DE[21]。对于长度为L的信号x={xi|1≤i≤L},首先通过NCDF将x归一化至yi=[y1,y2,…,yL],yi∈(0,1)。随后,将y映射到c个类别:
(11)
式中,r(·) —— 四舍五入函数

对映射序列zc进行相空间重构如下:
(12)
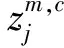
求解πv0v1…vm-1的概率:
(13)
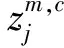
反向散布熵定义为:
(14)
2) 层次反向散布熵
对于信号X={x(1),x(2),…,x(N)},HRDE的计算过程如下。
(1) 定义一个算子Qj:
(15)
式中,j=0或1,Qj的形式取决于信号的长度。对信号给定算子有:
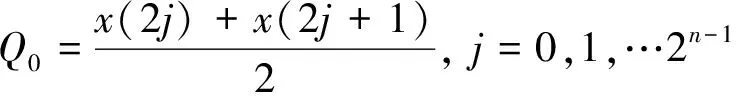
(16)
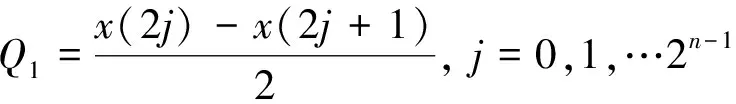
(17)
其中,Q0为信号在第一层分解的低频分量,Q1为信号在第一层分解的高频分量。
(2) 构建m阶向量[v1,v2,…,vm],其中vm=0或1,通过vm来表示整数e:
(18)
可知,e为不小于0的整数,对于给定的e有唯一向量[v1,v2,…,vm]与之对应。
(3) 定义信号X每一层的各个节点组分为:
Xm,e=Qv1·Qv2·…·Qvm(X)
(19)
根据定义可发现,算子Q0和Q1分别代表Haar小波的低通和高通滤波。对各个节点分量进行反向散布熵分析,即实现了信号X的层次反向散布熵计算。层次分析中节点X1,0和X2,0的反向散布熵即相当于多尺度反向散布熵中尺度为2和4时的反向散布熵。本质上,节点Xm,0对应于多尺度计算中2m尺度的反向散布熵,并且层次分析的右边节点计算的是信号的高频分量。因此,HRDE不但分析了信号的低频分量,还提取了信号的高频分量,避免了部分嵌入在高频分量里的故障信息被遗漏[22]。
1.3 蜜獾算法优化支持向量机
1) 蜜獾算法
蜜獾算法是一种模拟蜜獾觅食行为而提出的仿生优化算法[23-24]。蜜獾获取食物的方式分为两种:① 闻香+挖洞;② 跟随蜜鹍鸟。在此基础上,将蜜獾算法分为挖掘阶段和采蜜阶段。
(1) 初始化部分。初始化蜜獾种群(种群数量N)和方位:
xi=lbi+r1×(ubi-lbi)
(20)
式中,xi—— 种群中第i个蜜獾
r1—— [0,1]内的随机量
lb—— 寻优空间的下限
ub—— 寻优空间的上限
(2) 定义强度Q。强度与食物的聚集度和食物之间的距离相关:
(21)
R=(xi-xi+1)2
(22)
di=xfood-xi
(23)
式中,Qi—— 食物的气味强度
R—— 源强度或聚集度
xfood—— 食物的方位
xi—— 第i个蜜獾的方位
di—— 食物与当前蜜獾个体i的距离
(3) 更新密度系数。密度系数a控制时间变化的随机性,保证从探索到开发的稳妥过渡。更新密度系数a随着迭代次数的增加而减小:
(24)
式中,C—— 不小于1的常数,默认C=2
T—— 当前迭代规模
Tmax—— 最大迭代规模
(4) 更新蜜獾的方位。HBA的方位更新xnew分为两个阶段,分别是“挖掘部分”和“采蜜部分”。
在挖掘部分,蜜獾会执行类似心形的行为,心形运动能够基于下式进行模拟:
xnew=xfood+F×β×Q×xfood+
F×r3×a×di×
|cos(2πr4)×[1-cos(2πr5)]|
(25)
(26)
式中,xnew—— 蜜獾更新后的方位
β—— 觅食的能力,默认β=6
r3,r4,r5,r6—— [0,1]内的4个随机量
F—— 改变不同寻优角度的符号
在采蜜部分,蜜獾会尾随蜜鹍鸟达到蜂巢的行为能够基于下式进行模拟
xnew=xfood+F×r7×a×di
(27)
式中,r7为[0,1]的随机量。
2) 优化支持向量机分类器
针对支持向量机分类器的泛化性能和分类性能受到惩罚系数和核函数影响的问题,采用蜜獾算法对SVM的超参数进行寻优,构建HBA-SVM分类器,具体步骤如下:
(1) 获取故障特征,将其进行归一化,并划分为训练样本和测试样本;
(2) 设置HBA的参数,如Tmax,N,β,C,并初始化蜜獾种群的方位。通过HBA对SVM的惩罚系数和核函数(C,g)进行优化搜索,以训练样本的分类准确率最大为适应度函数fi,迭代寻优生成一组SVM的最优超参数,使得SVM分类器的分类性能最佳;
(3) 训练SVM分类器。将迭代得到的最佳超参数赋予SVM模型,输入训练样本对SVM进行训练,通过测试样本测试优化后的SVM模型,得到测试样本的识别结果。
2 机械设备故障诊断模型
为了充分利用机械设备的声信号,提高故障识别的准确率,开发了一种结合SPA和HRDE的机械设备声信号故障诊断方法,具体流程如下:
(1) 声信号获取是利用麦克风设备收集离心泵和滚动轴承在不同故障状态下的声信号,生成原始信号样本;
(2) 信号分解是利用SPA对声信号样本进行分解,得到趋势分量和去趋势分量,突出信号中的故障信息;
(3) 特征提取是通过计算趋势分量和去趋势分量的HRDE熵值,提炼信号的故障特征,得到特征样本;
(4) 故障识别是通过HBA优化SVM分类器,获得最佳超参数,利用归一化的特征样本对分类器进行训练和测试,得到测试样本的分类结果,最后评估模型的泛化性。
3 实验研究分析
本节对离心泵声信号数据集[25]和滚动轴承声信号数据集[26]两个不同的机械设备数据集开展了故障检测实验分析,两个数据集都来自印度Sant Longowal Institute of Engineering and Technology。实验运行的软件配置为Windows 10 64位操作系统,运行内存为16G,平台为MATLAB 2015 a,硬件环境为i5 12500 H,RTX 2050显卡。
实验中,SPA的正则化系数设置为λ=5,HRDE参数设置为嵌入维数m=3,类别个数c=6,延迟t=1,层次k=2。
3.1 离心泵故障诊断
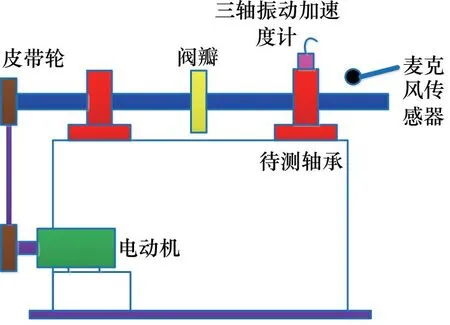
离心泵声信号数据采集自图1所示的实验装置,数据集在43 Hz的转速和70 kHz的采样频率下,利用麦克风设备,型号ECM8000,采集了离心泵的声音信号。离心泵设置了4种故障类型:叶轮缺损、叶轮堵塞、轴承内圈破损和轴承外圈破损,4种故障部件如图2所示。轴承是单列深沟球轴承,型号为6203ZZ。

图1 离心泵实验台

图2 离心泵4种故障部件[25]
对于该数据集,通过无重叠的采样来构建样本,为了获得信号在故障一个周期内的详细信息,每2048个数据点组成一个样本,构造的试验数据如表1所示,共有5种工作状态,分别是1个健康,4种故障。

表1 离心泵试验样本组成Tab.1 Sample composition of centrifugal pump test
离心泵5种状态的声音信号波形如图3所示。
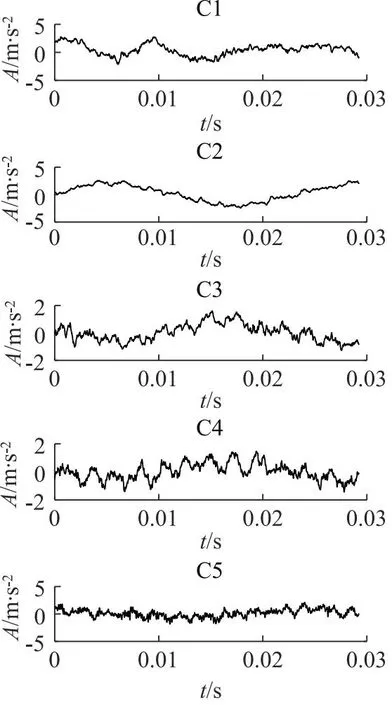
图3 离心泵各状态的时域波形
对5种状态的声信号进行SPA分解,得到对应的趋势分量和去趋势分量,结果如图4所示。
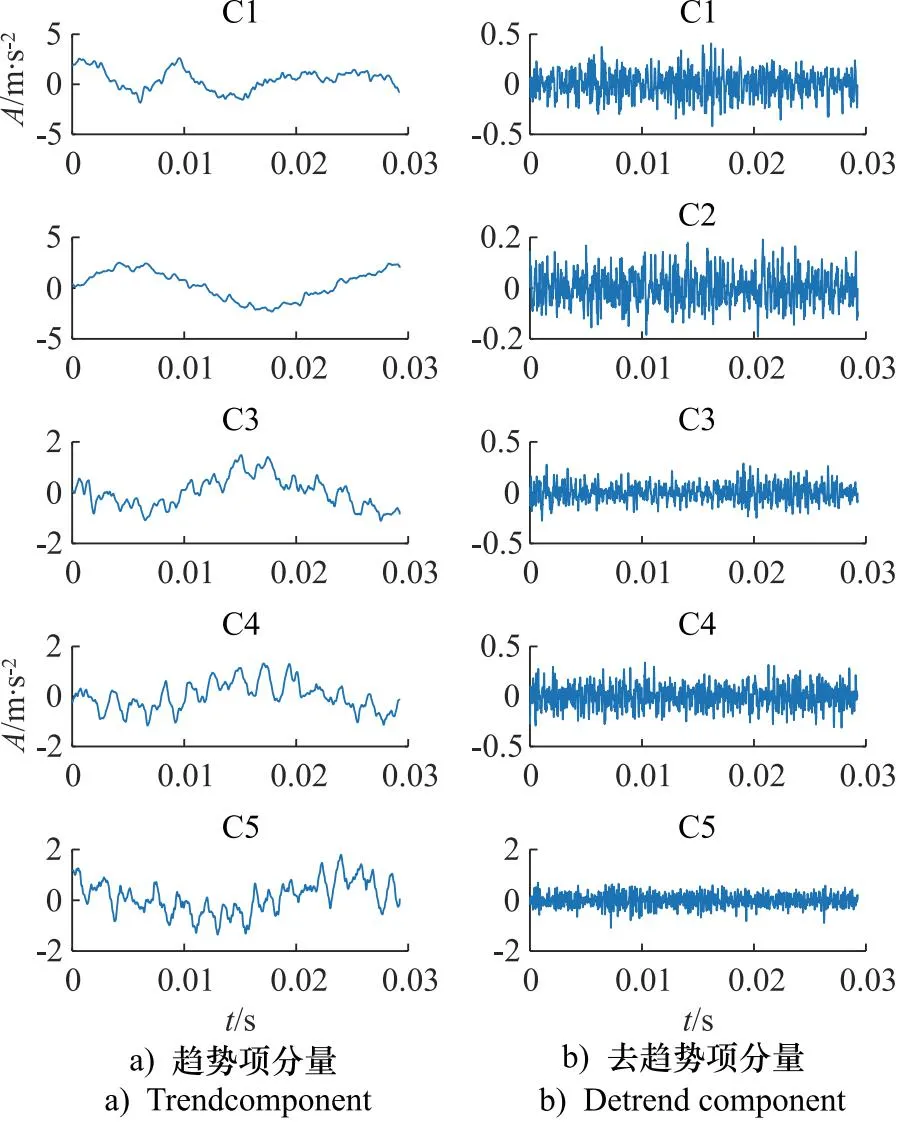
图4 离心泵声信号的趋势项和去趋势项分量
由图4可知,经过SPA分解后,声信号的趋势和去趋势项分量都实现了明显的分离,这证明SPA分解能够比较好的刻画信号不同尺度的特性。
随后,采用HDE提取趋势项和去趋势项分量的故障特征,如图5所示。
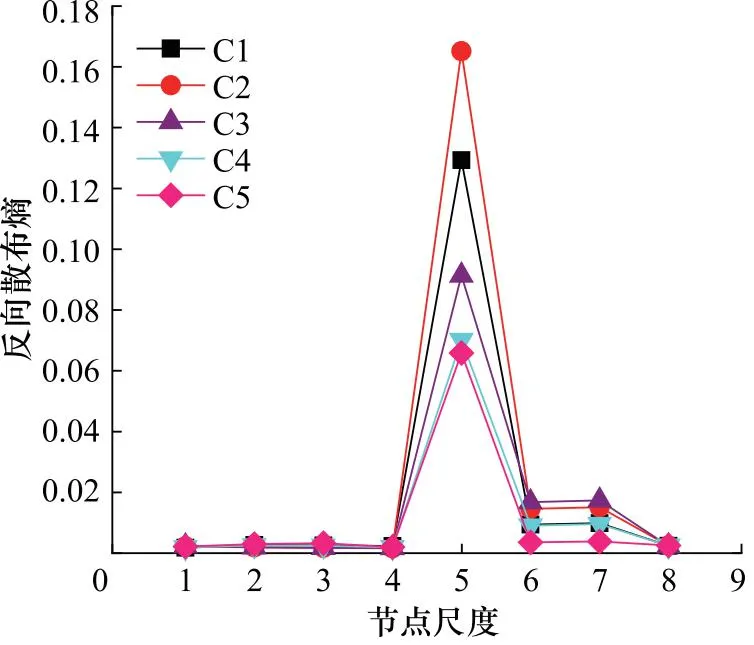
图5 离心泵5种状态的HRDE值
由图5可知,HRDE在部分尺度上能够较好的区分五种状态, 证明该方法能够用于区分不同离心泵故障,具有一定的有效性。
为了量化SPA-HRDE进行故障表征的性能,建立HBA-SVM分类器进行离心泵的故障识别。蜜獾种群规模为20,最大迭代次数为50,惩罚系数C和核函数参数g的搜索范围设置为[0.01,1]。训练样本和测试样本的比例设置为1∶1,即训练样本的数量为50,测试样本的数量也为50,将训练样本输入至HBA-SVM中进行训练,得到的最优C和g为0.935和0.068,则测试集的识别结果如图6所示。
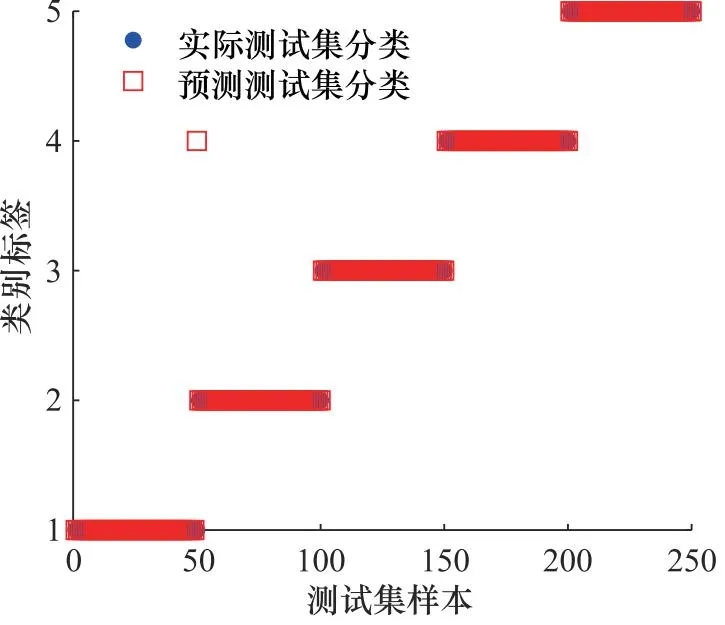
图6 基于SPA-HRDE与HBA-SVM识别结果
由图6可以发现,除了一个C1样本被误识别为C4样本外,其他全部样本的状态都实现了准确的判断,故障识别准确率达到了99.6%,这表明所提方法能够有效的判断离心泵的不同故障类型,具有一定的优越性。
为了验证SPA-HRDE方法进行故障特征提取的优越性,利用HRDE,EMD-HRDE,EMD-MRDE,SPA-HDE,SPA-MRDE和SPA-MPE故障特征提取算法进行对比分析。其中MPE的嵌入维数为6,时间延迟为1。
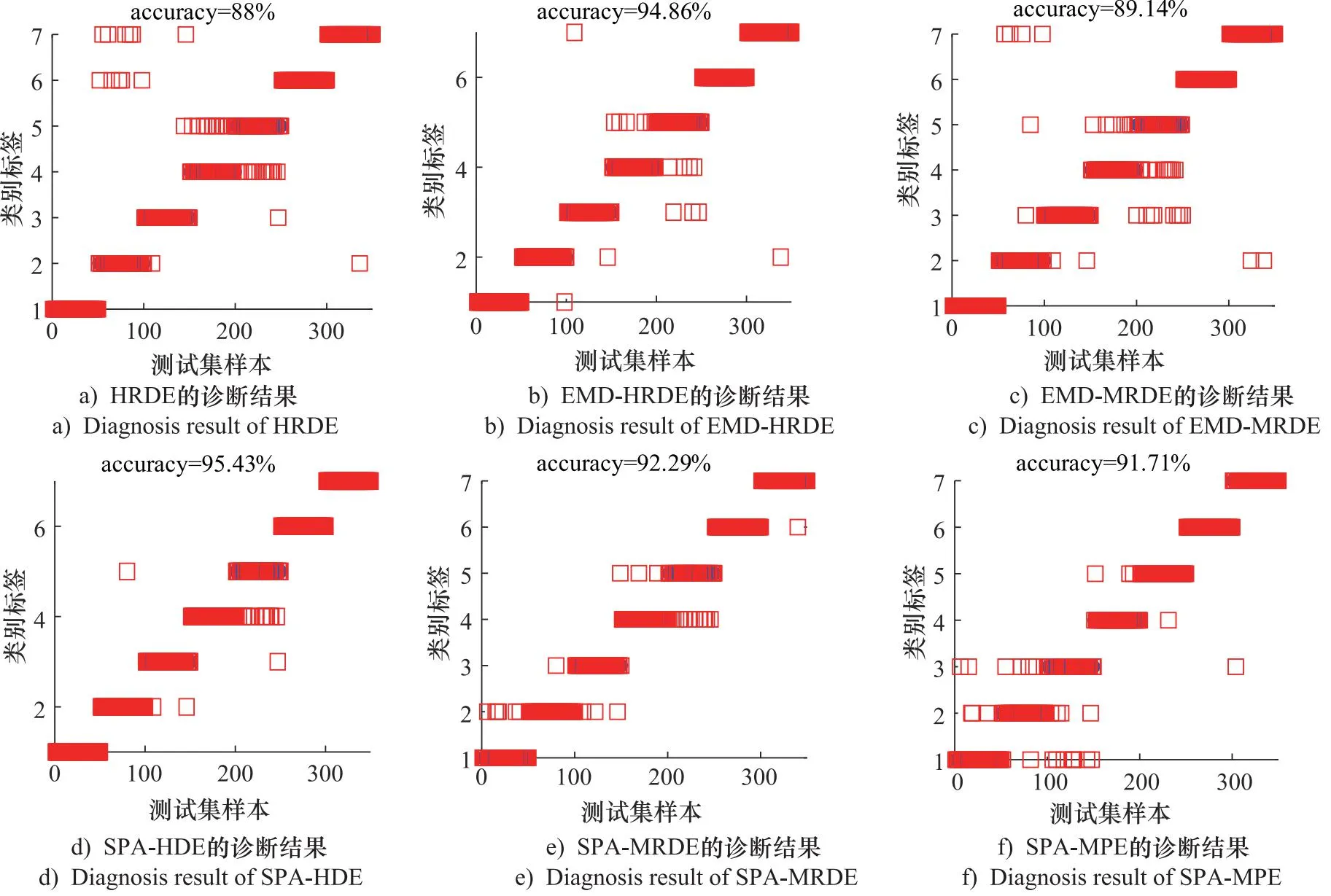
将上述6种故障特征提取方法提取的故障特征输入至HBA-SVM中进行故障识别,结果如图7所示。
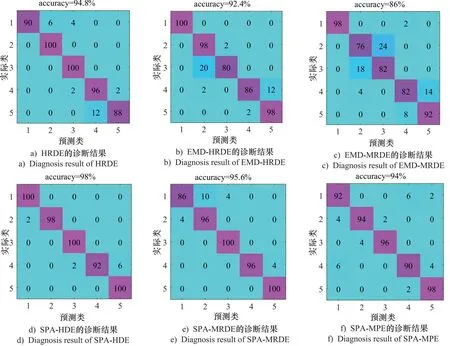
图7 六种方法的HBA-SVM识别结果
由图7可知,6种方法的识别准确率均低于所提方法,这证明所提特征提取方法是有效且优越的。图7a和图7b对比,EMD-HRDE的准确率低于HRDE,这是因为仅选取了前2阶模态分量进行特征提取,忽略了其他模态分量中的故障信息,相比于直接对原始信号进行分析,其造成大量故障信息被遗漏。而所提方法分解只得到了2个分量,不存在分量选择的难题,因而分析效率更高。
对比图7d、图7e和图7f,可知HRDE的性能优于HDE,MRDE和MPE方法,这与之前的分析相一致,即HRDE通过采用层次处理和反向散布熵相结合的分析,能够从信号中提取出更高质量的故障特征,从而优于这3种方法。总之,所提出的SPA-HRDE特征提取方法不仅避免了分量选择的问题,而且能够取得较好的特征提取效果。
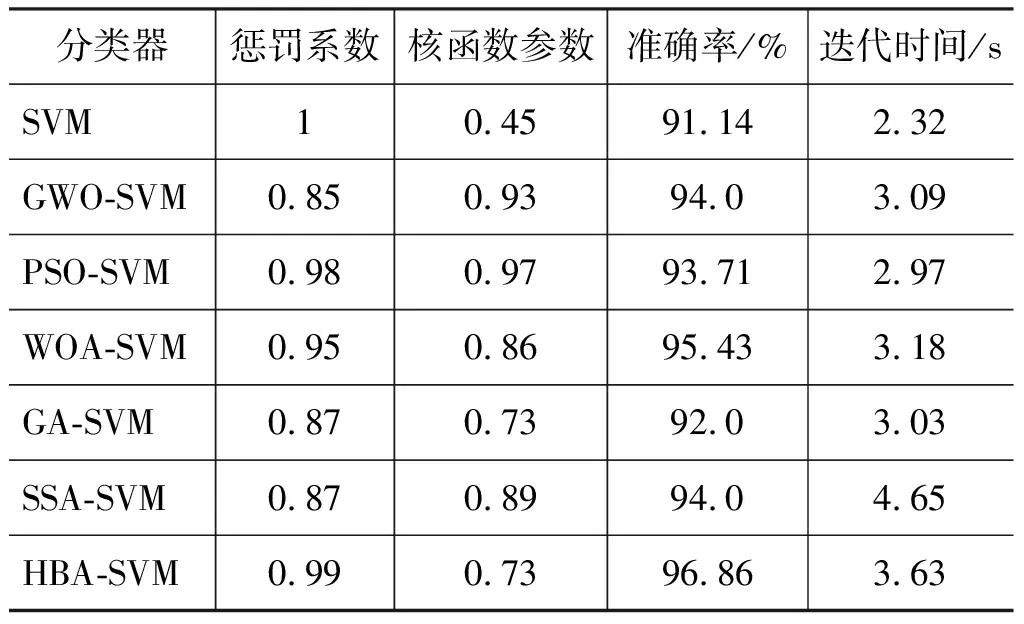
为验证HBA-SVM分类器的优越性和高效率,利用灰狼优化算法(GWO)、粒子群优化算法(PSO)、鲸鱼优化算法(WOA)、遗传优化算法(GA)和麻雀搜索算法(SSA)进行对比,6种优化算法的参数设置如表2所示。
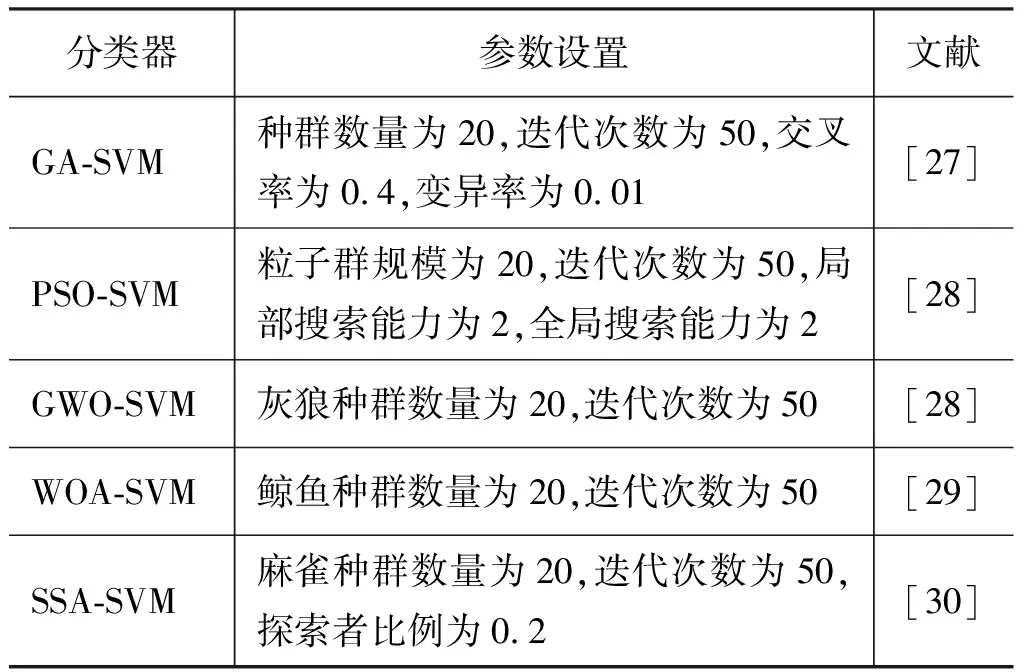
表2 优化算法的参数设置Tab.2 Parameter setting of optimization algorithm
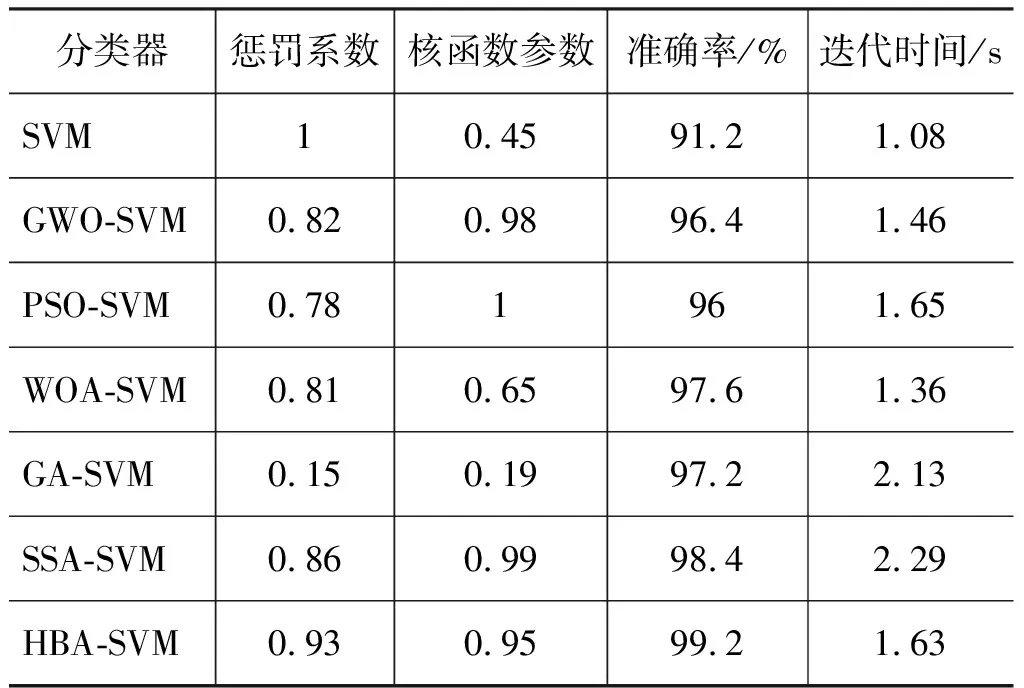
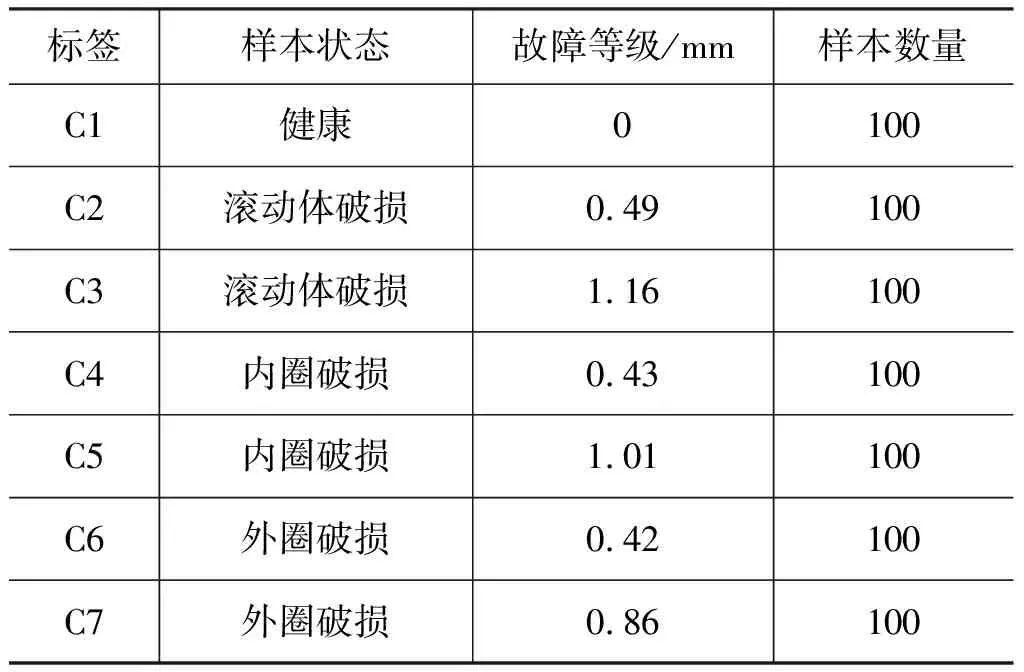
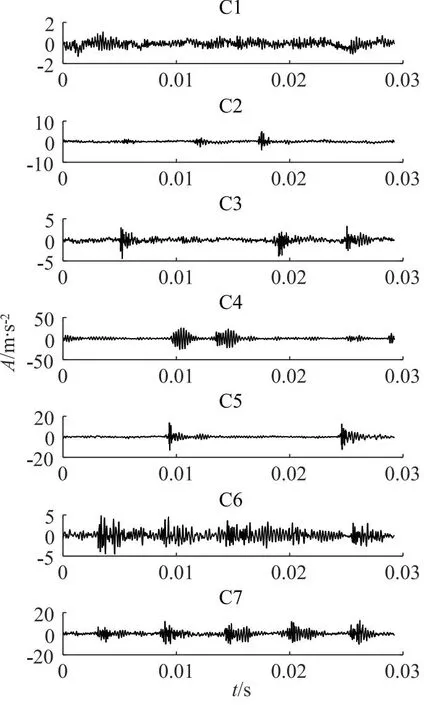
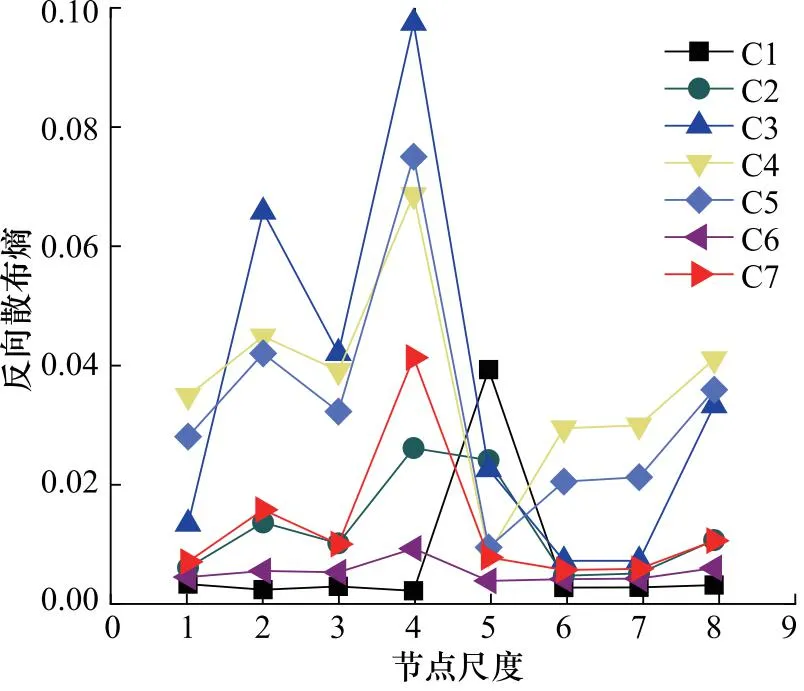
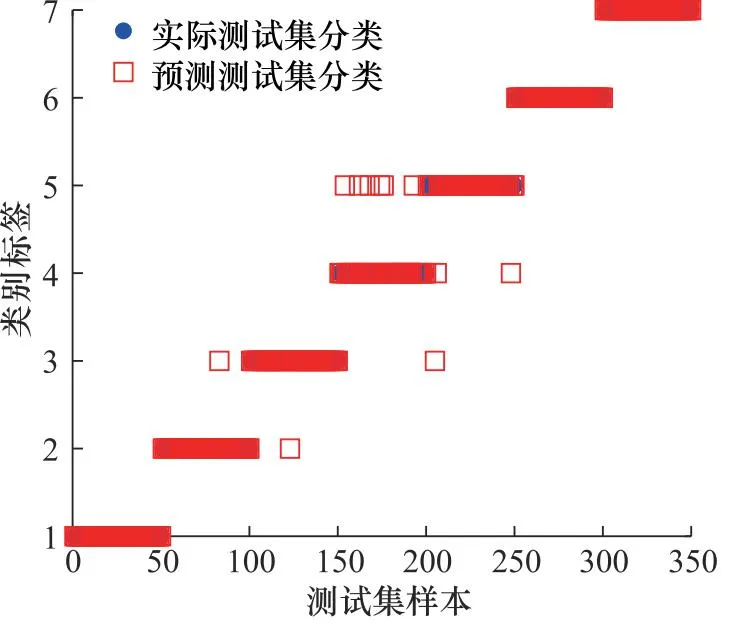
优化过程中的适应度迭代曲线如图8所示。可以发现,HBA-SVM和PSO-SVM均在第2次迭代时得到了各自的最优解,这表明HBA和PSO的收敛速度较快,但是PSO优化得到的结果是局部最优。GA-SVM优化曲线在第38次迭代时才获得最终的结果,GWO-SVM在第29次迭代时获得最终结果,2个算法的收敛速度较慢, 且优化得到的结果不是全局最优。从收敛速度和搜索性能来看,优化算法性能的排序为HBA 图8 优化适应度迭代曲线 经过6种算法优化出适应度最佳对应的C和g代入至SVM参数进行故障识别,C和g的优化取值及6种算法的诊断结果如表3所示。 表3 离心泵的不同分类器故障诊断结果Tab.3 Fault diagnosis results of different classifiers for centrifugal pumps 由表3可知,每种算法优化得到的2个参数不一致,而HBA-SVM的优化结果最佳,测试样本的准确率达到了99.2%。在优化的总时间上,WOA-SVM分类器的迭代时间最少,为1.36 s,而HBA-SVM的优化时长为1.63 s,仅高于WOA-SVM和GWO-SVM,低于另外3种分类器,这证明了HBA-SVM不仅具有较好的优化性能,而且效率也较高。此外,未优化的SVM取得了91.2%的准确率,低于其他优化后的SVM,这证明了优化的必要性。因为固定的参数设置无法适用于不同场景的分类识别问题。 本试验的滚动轴承声信号数据采集自图9所示的滚动轴承故障模拟试验台。 图9 滚动轴承试验装置 该数据集在2050 r/min的转速下以70 kHz的采样频率,通过型号为ECM8000的麦克风传感器,收集滚动轴承辐射的声信号。试验轴承为圆柱滚子轴承,型号为NU205E。设置3种故障状态,内圈破损、外圈破损、滚动体破损,如图10所示。每种故障状态包含2种故障尺寸,因此,总共包含7种工作状态,分别是1种健康,6种故障。 图10 轴承的4种健康状态视图[26] 利用无重叠的方式进行样本的构造,每个样本的长度为2048,构造好的实验样本如表4所示,共有7种工况,分为1个健康和6类故障。 表4 滚动轴承声信号样本Tab.4 Acoustic signal sample of rolling bearing 滚动轴承4种工作状态下的声音信号波形如图11所示。 图11 滚动轴承各状态的声信号波形 通过SPA对声信号进行循环分解,直至全部样本都完成分解,得到对应的趋势分量和去趋势分量。随后,采用HRDE提取趋势和去趋势分量的故障特征,如图12所示。 图12 滚动轴承7种状态的HRDE值 由图12可知,7种状态的熵值曲线出现了部分重叠交叉现象,如C4和C5样本具有相同的趋势,同时熵值非常接近。而其他几种状态的熵值曲线具有比较好的分离效果,能够很好的表征轴承的故障状态。 为了进一步量化SPA-HRDE方法的可行性,将其提取的故障特征输入至HBA-SVM中进行故障识别,随机从样本中抽取50组特征进行训练,将测试特征输入训练好的分类器进行诊断,如图13所示。 图13 基于SPA-HRDE与HBA-SVM识别结果 由图13可知:有4类轴承样本出现了识别错误,其中C2,C3和C5仅出现了一个错误样本,而C4出现错误的样本较多。C1,C6和C7样本的识别准确率为100%,总的识别准确率为96.86%,证明所提方法能够较为准确的识别轴承不同类型和损伤等级的故障,但在识别内圈故障时有效性较差。 随后,采用3.1节中的6种方法进行对比以验证所提的SPA-HRDE方法的优越性,将6种方法提取的故障特征进行HBA-SVM识别,如图14所示。 图14 6种方法的HBA-SVM识别结果 由图14可知,6种方法的识别准确率均低于图13所提方法,证明了所提方法的优越性。可以注意到,6种方法均无法完全识别内圈破损,出现了较多的识别错误样本,表明内圈破损信号的复杂度与其他信号比较接近,难以准确进行区分。此外,HRDE方法的识别准确率仅有88%,低于其他5种方法,这证明了采用EMD和SPA进行信号预处理的有效性。 为了对比不同优化算法的有效性和优越性,利用上节中的6种算法进行对比分析,对由SPA-HRDE提取的故障特征进行故障识别,具体的故障识别结果如表5所示。 表5 离心泵的不同分类器故障诊断结果Tab.5 Fault diagnosis results of different classifiers for centrifugal pumps 由表4可知,HBA-SVM分类器的诊断准确率最高,WOA-SVM次之,GA-SVM最低,这证明了HBA-SVM的优越性,根据迭代的时间来看,HBA-SVM的效率仅高于SSA-SVM,低于另外4种分类器,证明HBA-SVM的泛化性牺牲了效率,但彼此的效率相差不大,总的性能是能接受的。 针对现有机械设备故障诊断方法一般基于振动信号,而振动信号在获取时存在接触式采集,易对设备产生负面影响的问题,提出了一种基于SPA和HRDE的机械设备声信号故障诊断方法。研究结论如下: (1) 在进行SPA-HRDE进行特征提取的基础上,HBA-SVM模型的故障识别准确率达到了99.6%和96.86%,高于其他特征提取方法; (2) HBA-SVM分类器的诊断准确率优于其他分类器,而迭代速度彼此之间差距较小,因此HBA-SVM具有较优异的泛化性; (3) 所提出的基于SPA-HRDE和HBA-SVM故障诊断方法能够准确的识别离心泵和滚动轴承的故障类型,在诊断准确率和诊断效率方面具有一定的工程使用价值。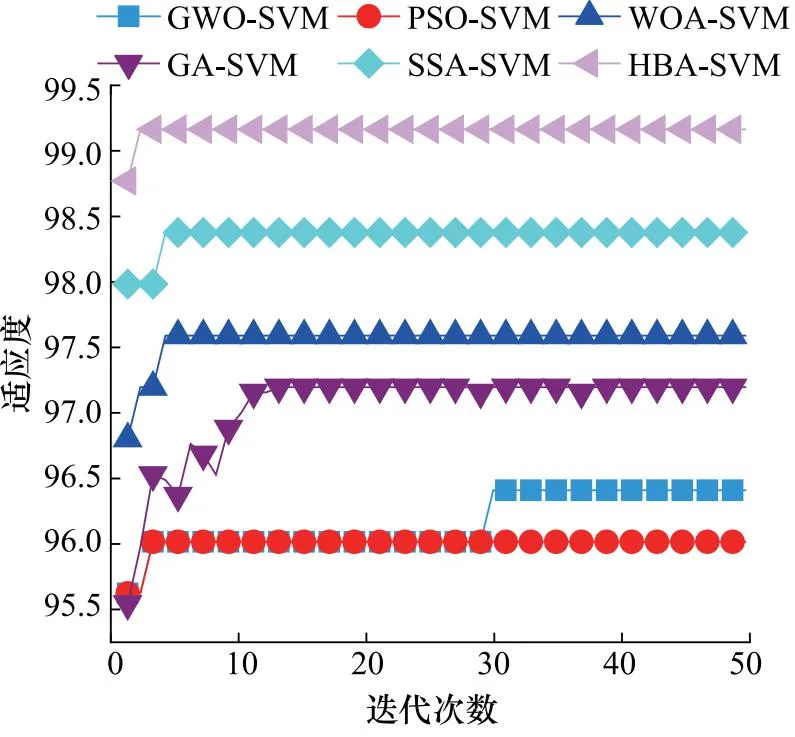
3.2 滚动轴承故障诊断

4 结论

