阀芯间隙固液两相流动特性及卡滞机理

林振浩, 聂家熙, 华霆锋, 金志江, 钱锦远

(浙江大学 化工机械研究所, 浙江 杭州 310027)

引言

阀芯作为阀门控制介质流动方向和流动截面积大小的关键部件,决定着流动介质的流量、压力等参数的调节和控制[1]。然而,当阀芯受到过大的阻力时,阀门的响应时间增加,动作迟缓,甚至导致阀芯出现卡滞。值得注意的是, 当流体中混入外部污染颗粒或自身磨损产生的固体颗粒时[2],容易随着流体进入阀芯配合间隙中,从而导致阀芯发生卡滞甚至卡死,严重威胁整个系统的稳定性和安全性。尤其以液压阀卡滞故障报道最多,例如在液压系统中由液压控制阀卡滞所引起的故障占推土机液压系统总故障的22%左右[3]。值得注意的是,在液压系统中,大约有70%的故障是由油液污染引起的,其中固体颗粒引起的故障占总污染的60%～70%[4]。因此,本研究以液压滑阀为研究对象,着重探讨污染颗粒引起的阀芯卡滞现象。

污染颗粒随流体进入阀芯配合间隙后,部分颗粒随着流体流出间隙,部分存留于配合间隙中。因此,对污染颗粒的流动特征分析是十分重要的。范家辉等[5]分析了综合传动定压滑阀配合间隙内颗粒的流动特性和泄漏量变化规律,建立了泄漏量与颗粒浓度的预测公式。赵春玲等[6]分析了U型槽、矩形槽和三角形槽对液压阀配合间隙内固体颗粒浓度分布的影响,发现带有圆角的三角形槽的流动更加流畅,藏污能力强。薛殿伦等[7]分析了阀芯阀套间隙热变形后含污染颗粒的油液在间隙中的流动和卡滞情况。徐瑞等[8]基于欧拉模型研究了颗粒直径对配合间隙内颗粒分布的影响规律。范帅等[9]使用NAS计数法计算污染油液中颗粒分布规律,尺寸为5～15 μm的颗粒占总数的97.3%。TERRELL等[10]提出了一种预测材料磨损颗粒的运动学轨迹模型,并将计算预测结果与其他研究者进行的实验数据进行了比较,验证了预测模型的正确性。

配合间隙内污染颗粒的存在,使得阀芯产生较大的卡滞力,进而影响阀芯的运动性能。周正[11]对大量实验数据进行分析,确定了阀芯卡滞力达到最大值的“敏感颗粒”直径。褚渊博等[12]分析了污染颗粒特征参数对偏导射流式压力阀卡滞摩擦力的影响规律。陈大为等[13]研究了滑阀密封间隙内颗粒特征参数对阀芯摩擦力的影响。刘志强等[14]研究了滑阀配合间隙的敏感间隙范围,在该敏感间隙范围内阀芯的卡滞力最大。以上研究大多是液压阀卡滞的理论、定性研究,较少关于阀芯卡滞力定量化的分析。

本研究以典型的液压滑阀为例,基于欧拉-欧拉固液两相流模型,分析阀芯阀体配合间隙内污染颗粒固液两相流动特性及阀芯卡滞规律。建立阀内跨尺度流域并获得配合间隙的边界条件,计算获得跨尺度流域内的流动特性。建立带有均压槽的配合间隙流域模型,分析颗粒特征参数(颗粒浓度、颗粒直径)对配合间隙内颗粒分布及阀芯卡滞力的影响规律,为减小阀芯卡滞措施的研究提供参考。

1 数值模型

1.1 欧拉模型

本研究以含污染颗粒的油液为介质,采用欧拉-欧拉模型求解阀内及配合间隙内固液两相流动。在计算流体动力学中,欧拉-欧拉模型常用于求解多相流动及相间的相互作用,其计算精度相比于混合模型更高[12]。

欧拉模型中第k相的连续性方程为：

(1)

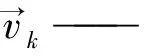
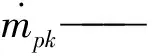
欧拉模型中第k相的动量方程为：

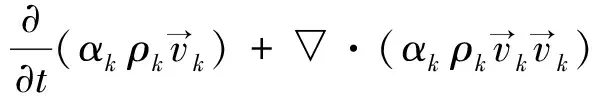
(2)

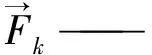
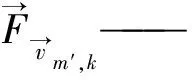
p—— 各相共享的相同压力

(3)

式中,μk,λk—— 第k相的剪切黏性系数和体积黏性系数

由连续性方程可得到每一相的体积分数方程：

(4)

式中,ρk为相参考密度,即流域第k相的体积平均密度。

1.2 计算域和网格

在液压阀中,以滑阀最为常见,如图1所示,本研究的滑阀主要由阀芯和阀体组成,阀芯上开设多个均压槽,阀芯沿轴向运动实现启闭。由于流域的对称性,在不考虑阀芯配合时的偏心、倾斜及倒锥等情况的影响,将滑阀模型简化成跨尺度的二维流域模型,包括阀腔内的流域和配合间隙的流域。在跨尺度流域模型中省略了间隙内的均压槽,如图2a所示。同时,为了引入配合间隙内的椭圆型均压槽,单独建立了带均压槽的配合间隙流域模型,如图2b所示。

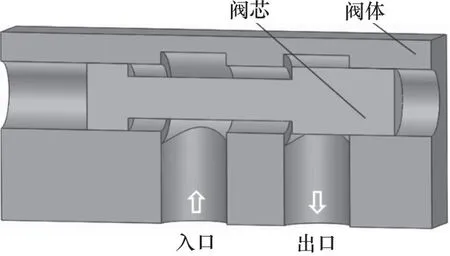
图1 液压滑阀几何模型

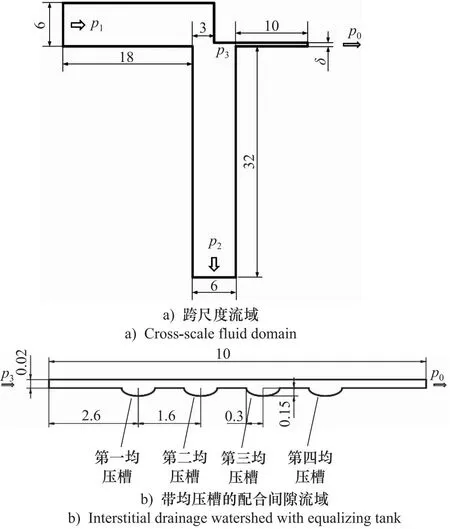
图2 计算模型

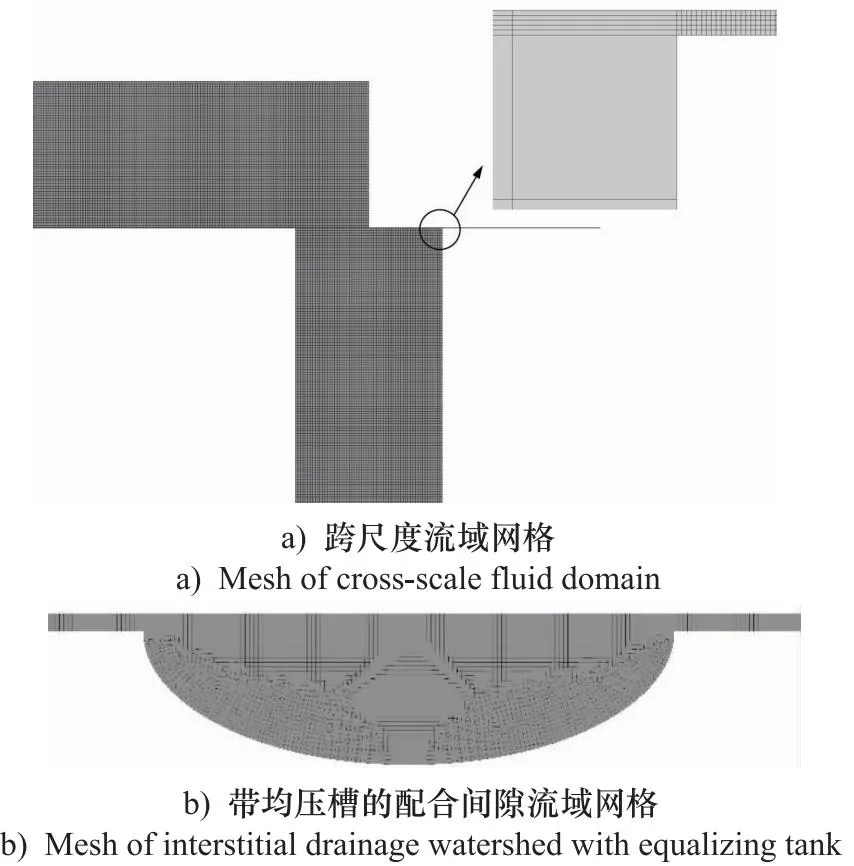
图3 流域网格划分

对流域进行离散化时, 单元格为四边形结构化网格。跨尺度流域的间隙网格进行细化和过渡,总体网格数量为41000。带有均压槽的配合间隙流域间隙为20 μm,因此网格尺度给定5 μm,间隙网格层数为4层,网格数量为19576。

1.3 边界条件及计算设置

流体介质为含污染颗粒的油液,阀内流动为固-液两相流。假设流体为不可压缩、恒定流动牛顿流体。第一相为油液,密度ρ为900 kg/m3,动力黏度μ为0.0405 Pa·s;第二相为理想球体的固体颗粒,密度为ρ为7500 kg/m3,动力黏度μ为10-5Pa·s。在欧拉模型中可设置不同的颗粒直径,本研究中选取3～18 μm 的颗粒间隙。对于跨尺度流域的边界设置,入口采用压力进口p1为10 MPa,同时进口设置为不同的颗粒浓度(即颗粒体积分数),本研究选取颗粒体积分数1%,3%,5%,7%。阀腔流域的出口采用压力出口p2为9 MPa,配合间隙流域的出口采用压力出口p0为0。壁面采用无滑移条件。欧拉模型中,固-液两相之间曳力函数选择Syamlal-o’brien。Phase interaction中的Drag选Schiller-naumnn,Lift选择none即不分离相。采用标准k-ε湍流模型。

在带有均压槽的间隙流道计算中,根据雷诺数的计算,其远小于同心环状缝隙的临界雷诺数,故流体在间隙流动为层流,黏性模型采用Laminar模型,进口压力采用跨尺度流域计算得到的压力p3,出口压力为p0。颗粒直径和颗粒体积分数设置与跨尺度流域边界设置相同。

2 结果与讨论

2.1 颗粒跨尺度流动分析

图4显示了颗粒直径为3 μm、进口颗粒浓度3%的流场云图。可以看出,油液流经节流口时,流速急剧增加,在此处形成高速射流,最高速度大于50 m/s,同时压力减小。这是由于在节流口处流域截面突然变小,节流面积减小。油液经过节流口后,在射流与壁面之间形成旋涡,如图4b所示。由配合间隙流场放大图可以发现,间隙入口处的压强为8.56 MPa,通过配合间隙逐渐减小至0。

图4 跨尺度流域流场云图

在间隙中油液以缓慢的速度向外流动,间隙进口速度小于5 m/s,然而在节流口处最大速度大于50 m/s。因此,在跨尺度流域中压力和速度产生剧烈变化。在油液黏性作用下间隙尺寸较小导致流体质点之间以及流体质点与壁面之间产生摩擦,增加了沿程损失。同时由于流经节流口后进入配合间隙,其流域尺度发生急剧变化,导致流体质点间以及流体质点与壁面之间的撞击加剧,引发较大的压力损失,增加了局部损失。

提取间隙中心线上的颗粒体积分数,图5是进口颗粒浓度3%时污染颗粒直径与配合间隙内颗粒体积分数φ的关系图。从图中的放大云图可知,配合间隙内的颗粒分布不均匀,中心区域的颗粒体积分数比壁面附近的高。这是因为黏性作用使得壁面存在摩擦力,导致中间区域的速度比壁面附近的速度大。从曲线可以看出,配合间隙内的颗粒体积分数均高于0.03,存在颗粒聚集现象,特别是间隙入口处。沿着流体流动方向,颗粒体积分数呈下降的趋势。随着颗粒直径的增大,配合间隙内颗粒体积分数逐渐增大。这是因为随着颗粒直径的增大,同样颗粒数量和密度下所占用的空间体积也越大,其颗粒质量和惯性越大,在涡流和压差作用下更加容易进入间隙。

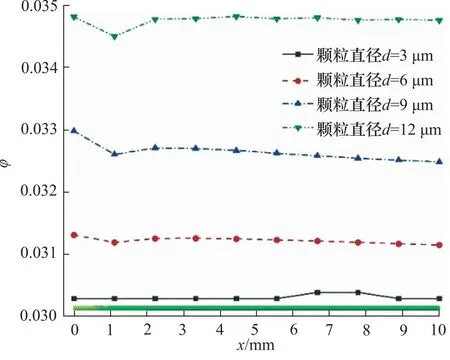
图5 不同颗粒直径下间隙颗粒体积分数分布

2.2 颗粒直径对间隙流动的影响

为了更加深入的研究颗粒进入间隙后的分布情况,选取了带有均压槽的间隙模型进行仿真计算。以间隙进口的中心为原点建立坐标系,提取间隙中心线上的颗粒体积分数,如图6所示。图6显示了进口颗粒浓度为3%时不同颗粒直径下配合间隙内的颗粒体积分数的变化曲线。以颗粒直径3 μm为例,油液进入第一均压槽前的间隙内颗粒体积分数为进口设定值0.03,而后面相邻均压槽之间的间隙内颗粒体积分数约为0.0302。这是因为进口压力较高,第一段间隙的进出口压差较大,如图7所示,颗粒在压差的作用下随着油液进入第一均压槽,沿着流动方向,压降降低,部分颗粒在间隙内发生滞留。从图6中可知,均压槽内的颗粒体积分数最高,且随着颗粒直径的增大峰值也增大,这是由于油液进入均压槽时,流道变宽,流速减小,在均压槽处颗粒滞留。沿流动方向,不同的均压槽内的峰值也不同,从第一均压槽到第四均压槽,其峰值是增加的。

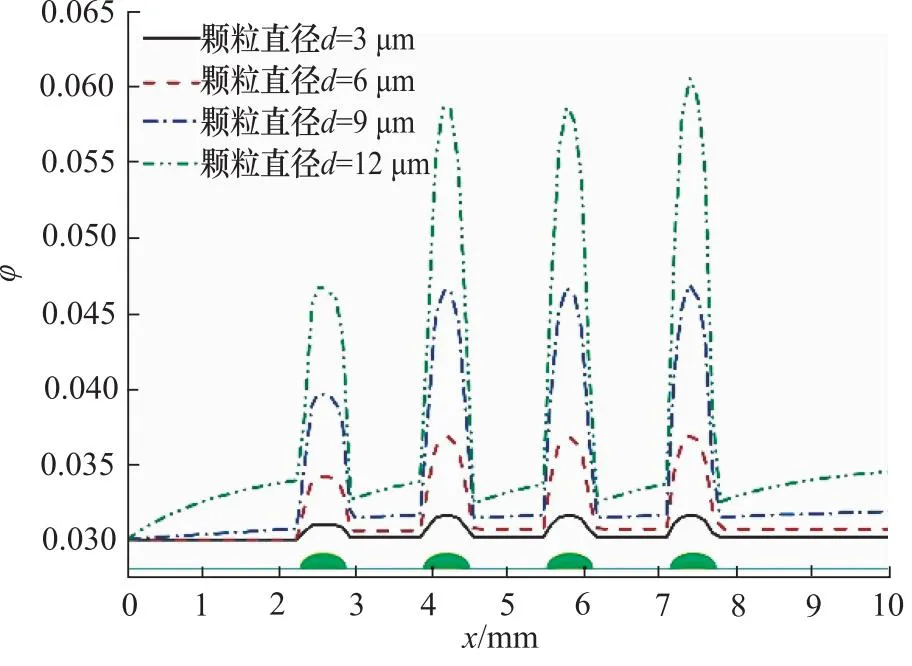
图6 不同颗粒直径下带均压槽间隙的颗粒体积分数

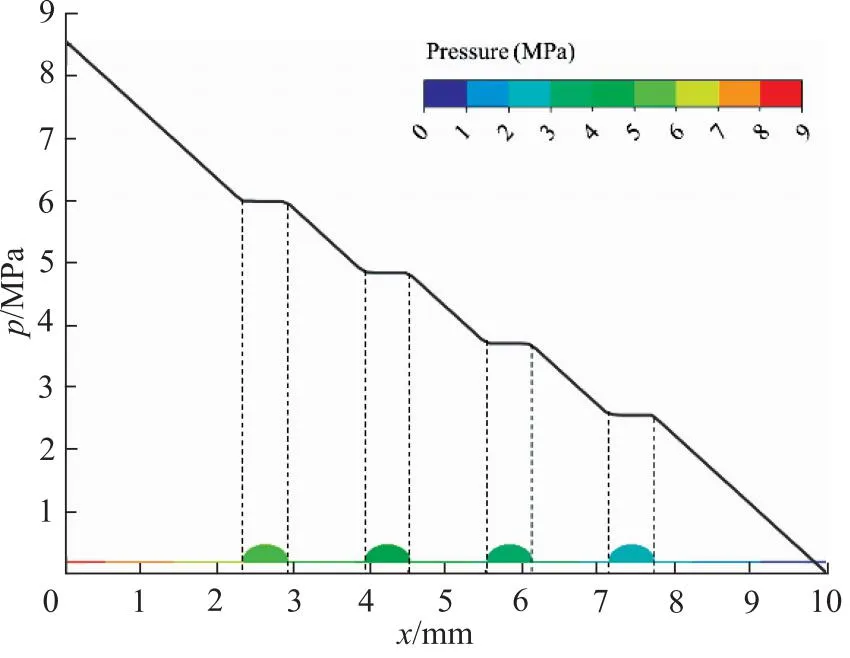
图7 颗粒直径3 μm、颗粒浓度3%时的间隙压力分布

2.3 颗粒特征参数对阀芯卡滞力的影响

含不同颗粒直径的油液在配合间隙流场过滤下,污染颗粒体现出不同的聚集效应,从而影响阀芯卡滞力f(即阀芯表面摩擦力)。通过Fluent中的后处理提取并计算了不同颗粒体积分数和颗粒直径下的阀芯卡滞力。图8是不同颗粒浓度下阀芯卡滞力随颗粒直径的变化图。从图中可知,随着颗粒直径的增加,阀芯卡滞力呈现先增大后减小的趋势。当颗粒直径在12 μm时,阀芯卡滞力达到了最大值,颗粒在9～15 μm时,颗粒阀芯卡滞力较大。因此,当配合间隙为20 μm时,定义颗粒直径12 μm为“敏感颗粒直径”,此时产生的阀芯卡滞力最大。随着颗粒浓度的增加,阀芯卡滞力也在增大,尤其在颗粒浓度为7%时,“敏感颗粒直径”为9 μm。颗粒直径为12 μm时,1%颗粒浓度时阀芯卡滞力为4.792 N,而颗粒浓度增加至7%时,阀芯卡滞力增加至4.798 N。阀芯卡滞力过大容易造成滑阀的卡紧甚至卡死。

图8 阀芯卡滞力随颗粒直径的变化曲线

3 结论

本研究以典型的液压滑阀为例,基于欧拉-欧拉固液两相流模型,分析阀芯阀体配合间隙内污染颗粒固液两相流动特性及阀芯卡滞规律。分析了跨尺度流域内含污染颗粒的油液流动特性。油液流经节流口时,由于节流面积变小,流速增大,在节流口处出现射流现象。油液从阀腔流域到间隙流域过程中,压力和速度产生剧烈变化。配合间隙内的颗粒体积分数均高于0.03,存在颗粒聚集现象,特别是间隙入口处。随着颗粒直径的增大,配合间隙内颗粒体积分数逐渐增大。同时,研究了颗粒特征参数(颗粒浓度、颗粒直径)对配合间隙内颗粒分布及阀芯卡滞力的影响规律。均压槽内的颗粒体积分数最高,且随着颗粒直径的增大峰值也增大。从第一均压槽到第四均压槽,均压槽底部的颗粒体积分数逐渐降低。随着颗粒直径的增加,阀芯卡滞力呈现先增大后减小的趋势。当配合间隙为20 μm时,颗粒直径为12 μm时的阀芯卡滞力最大,为敏感颗粒直径。阀芯卡滞力随随着颗粒浓度的增加而增加。