液力变矩器轴向力三维流动计算及验证
金 宸, 刘 城,2, 闫清东,3, 魏 巍,4
(1.北京理工大学 机械与车辆学院, 北京 100081; 2.北京理工大学 车辆传动重点实验室, 北京 100081;3.北京理工大学 前沿技术研究院, 山东 济南 250300; 4.北京理工大学 重庆创新中心, 重庆 401135)
引言
液力变矩器是一种常用的液力元件,由于具有无级变速变矩、自动适应等优良传动特性,被广泛的使用在工程机械、特种车辆中。液力变矩器内部流场流动规律非常复杂,其工作部件形状复杂,在运转时会出现数值很高的轴向力,这种轴向力的产生是由于工作液体在3个叶轮之间循环流动,而叶轮的表面积在轴向上不平衡,从而使叶轮整体呈现一个沿轴向向左或向右的轴向力[1]。这种轴向力作用在液力变矩器内部的轴承和连接件上,会大大缩减轴上部件的使用寿命,对传动的可靠性和寿命影响很大。
目前国内学者针对液力变矩器的轴向力计算,朱建华等[2]采用一维束流理论进行分析,简化液力变矩器的内部流场,对各个工作轮的轴向力进行计算并给出了理论计算公式和变化规律。闫清东等[3-5]采用CFD数值模拟的方法对液力变矩器流场进行计算,并且探讨了卸荷孔对轴向力的影响规律以及油液温度对变矩器性能的影响;ZHU等[6]研究了叶片角度对液力变矩器性能的影响;WANG等[7]构建了抑制模型限定了液力变矩器循环圆直径并且考虑了传动系统的综合效率问题。HEMPY[8]和DE JESUS RIVERA等[9]在变矩器内部安装了29个压力传感器,研究了液力变矩器的内部流场中压力分布与转矩的关系;E.EJIRI等[10-11]同样采用CFD方法计算变矩器的流场,发现能量损失主要出现在泵轮区域,因此泵轮入口处出现流速较低的区域,且液力变矩器效率的变化与此处能量的损耗相关。试验的方法同样被广泛的使用,才委等[12]采用PIV技术针对不同工况的泵轮内部流场进行采集,并制成二维图像;柴博森等[13-14]利用高速相机揭示了液力变矩器内部的真实流动,实现了对流场瞬态变化的观测。另外,在液力变矩器研究的前沿方向中,油液空化对液力变矩器的影响也不容忽视,郭猛等[15-16]发现空化效应主要出现在液力变矩器的导轮区域,且受油液温度影响,温度越低,空化越剧烈。
在以往的研究中可以发现,单纯的使用数值计算方法对液力变矩器的外特性预测是准确合理的,但是对于液力变矩器内部所产生的轴向力预测而言,其内部充满着复杂流道,这些流道对液力变矩器的外特性影响不大,很多只是起到润滑作用,但这些流道由于高压所产生的轴向力不能忽略。相比于只考虑3个叶轮的三维流场模型,轴向力计算模型更加复杂,需要考虑的流道更加多样。
但目前的研究仅对三维流场分析和理论计算结果进行对比,没有轴向力测试数据对比,且对各叶轮所受轴向力构成理解不足。泵轮与液力变矩器很多部件通过螺栓固连在一起,形成的流道复杂且没有规律,这些流道产生的轴向力是总轴向力中的重要一部分;导轮叶片两侧结构较为简单且对称,但导轮所有壁面完全浸泡在工作液体中,轴向力相对于流场变化更加敏感。因此,为探究准确的液力变矩器轴向力和组成,本研究建立了液力变矩器轴向力三维流场预测模型,并开展轴向力测试,在此基础上研究不同运行工况对轴向力的影响。
1 预测模型
液力变矩器内部流道分为4部分:泵轮流道、涡轮流道、导轮流道、泄漏区流道。从理论上讲,液力变矩器的CFD计算模型包括所有复杂流道与实际液力变矩器中的流道完全相同得到的结果是最为准确的结果,但是在实际建模中,过于复杂的流场结构会导致计算时间大大增加得不偿失,因此对于泄漏区流场只需要考虑主要流道如图1所示ch段、ai段、fj段等。

图1 泄漏区示意图
以某有效直径为420 mm的液力变矩器为研究对象,设置轴向力方向向左为正、向右为负,即使泵轮靠近涡轮的力为正,如图2所示。此液力变矩器中,泵轮叶轮、涡轮叶轮、导轮叶轮在中心处共同组成内泄漏区;闭锁离合器与涡轮毂、闭锁离合器与涡轮叶轮、涡轮毂与导轮、泵轮毂与导轮之间形成的流道区统称为外泄漏区,其中闭锁离合器中摩擦片之间包含许多微小流道,这些微小流道产生的轴向力全部在闭锁离合器总成中相互抵消不作用在泵轮或涡轮上,所以在建立流场模型的时候忽略这一部分的影响。
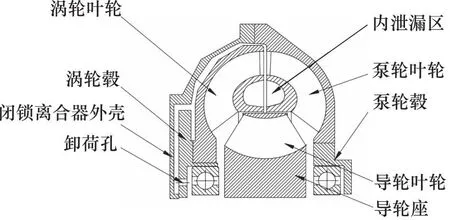
图2 液力变矩器结构简图
此流场模型由泵轮叶栅、涡轮叶栅、导轮叶栅与内外泄漏区4部分构成,如图3所示。油液在泵轮-涡轮-导轮之间循环构成液力变矩器主循环,外泄漏区的油液从涡轮毂卸荷孔中流向叶栅汇入主循环从而构成泄漏区副循环,副循环的流量少但旋转速度高,因此产生较高的离心油压。

图3 流场模型
在数值计算之前,首先进行网格独立性分析及液力性能预测精度验证,如图4所示。结果表明,随着网格尺寸降低,同一工况下涡轮仿真力矩呈现上升趋势,当网格尺寸达到1 mm后趋于稳定,且其计算结果与网格尺寸为0.5, 0.75 mm时相近,但网格尺寸低于1 mm 时计算成本过高,综合考虑下选1 mm作为网格尺寸。基于网格独立性分析选取的网格尺寸,在不同工况下对比变矩比K的计算结果与试验结果,如图4b所示。可见,在传动比i为0~0.8时,仿真结果与试验数据吻合较好,相对误差均在3%以内,证明了基于网格独立性验证的数值计算模型具有良好的可信度。
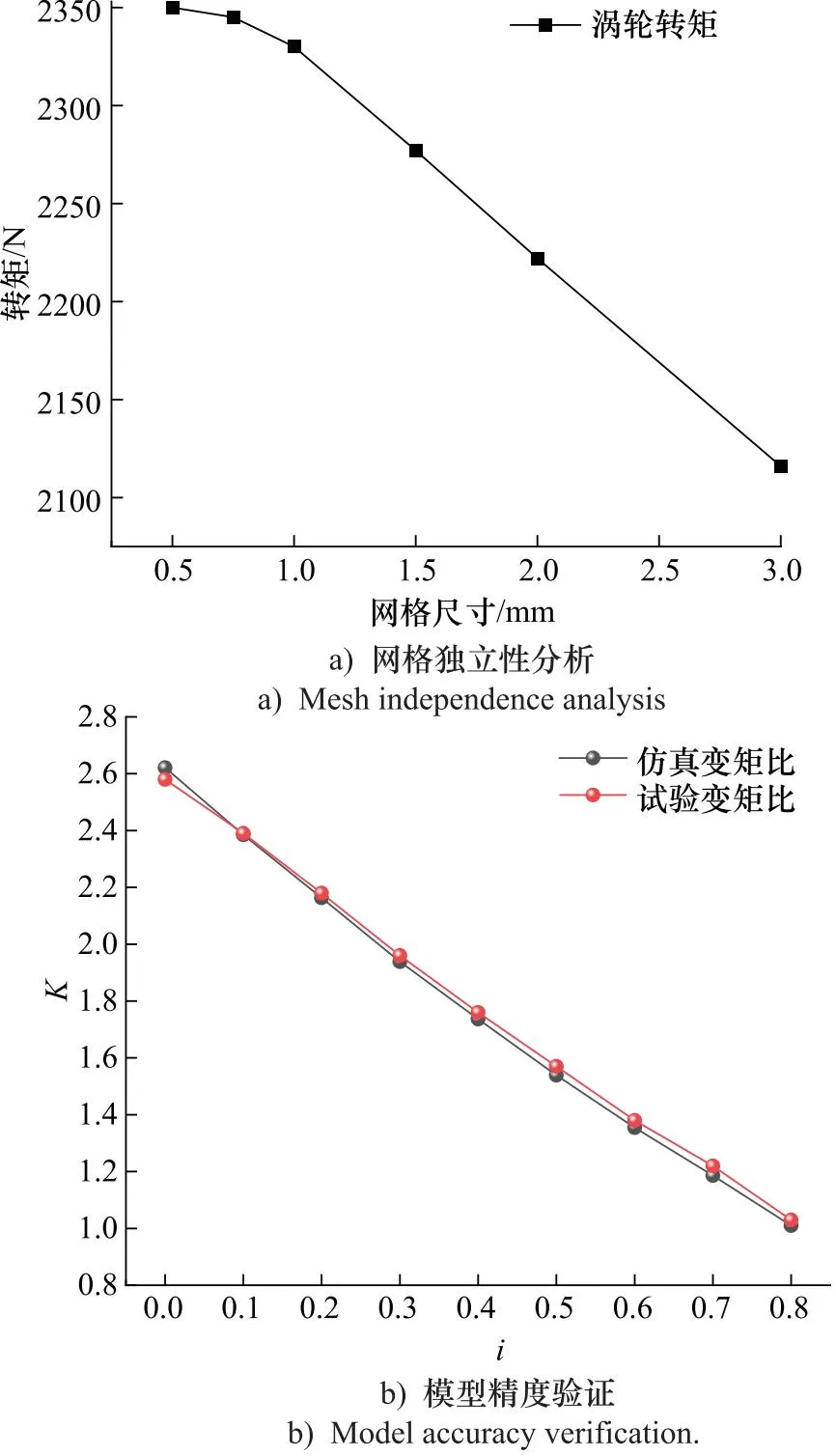
图4 数值模型可信度分析图
2 流场分析
以泵轮转速1800 r/min,传动比在0~0.8范围内以0.1间隔变动。湍流模型选择SST模型,各个工作腔壁面与叶轮表面视为刚体表面无变形,设置为无滑移壁面,泄漏区整体随泵轮转动,其中与涡轮或导轮接触的壁面需要设置相对速度以保证与实际运转情况的良好拟合。在传动比i为0~0.8工况下,泵轮轴向力的平均值为10567.74 N,涡轮轴向力的平均值为-1639.64 N,导轮轴向力的平均值为-8899.34 N,涡轮轴向力远小于泵轮与导轮的轴向力,因此本研究重点对泵轮、导轮轴向力进行分析。
变矩器正常工作状态是有进油口和出油口的,且进油口出油口有较为明显的压差,压力值的大小对轴向力的模拟十分重要,因此在进行仿真时需要考虑进出口,在模型中设置进出口,以进出口的压力值为条件,在试验中进油口的压力值在0.6 MPa左右变化不大,而出油口的压力值随着传动比增加而降低,因此以试验测得的压力值设置模型的进出口条件,如图5所示。

图5 进出口压力图
图6为传动比i=0, 0.5, 0.8时变矩器内流场与泄漏区的压力分布图,当i=0时此时涡轮和导轮静止不动,只有泵轮和泄漏区在高速旋转,所以变矩器的能量大部分消耗在内部流动中的碰撞当中,在内流场中最大压力出现在泵轮出口处,随后压力沿涡轮-导轮逐步下降,在泵轮入口处达到压力最低;在泄漏区压力分布图中可以看到泄漏区相对于工作轮流道处于整体高压的状态而且液体流动性差,传动油被挤压在泄漏区的各个缝隙当中,左侧的高压外泄漏区压力梯度明显,以泄漏区最上方的压力为基准,压力在左侧泄漏区逐渐下降;在导轮两侧泄漏区中可以看出明显的导轮左侧压力整体大于右侧压力。
青春期是学生生长发育的第二高峰期,身体正处于快速生长、发育完善阶段,身体各部分的机能、比例由稚嫩逐渐趋向成熟。加上中学生生理和心理上的急剧变化,给他们带来了更多的新问题和困扰。在平时的教育教学工作中,我们注重加强对学生进行心理健康辅导和思想教育工作,注重了心,忽略了身,并没有实现真正的身心结合教育。
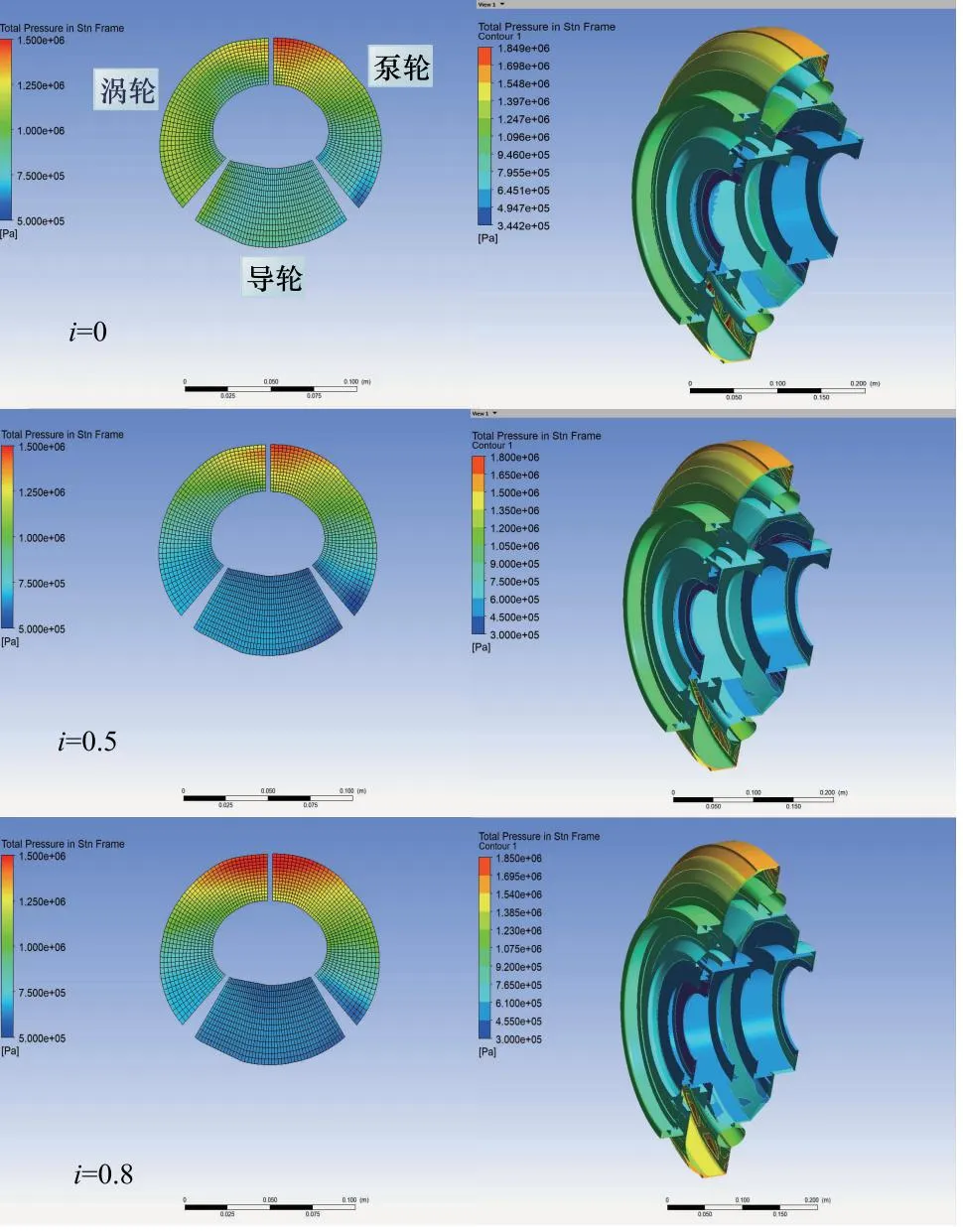
图6 内流场与泄漏区压力分布图
当i=0.5时,由于泵轮转速恒定,所以与i=0时的内流场压力分布图对比可以看到两者的泵轮流道压强分布大致相同,但是随着涡轮转速的增大,在涡轮入口处的压力增加明显,压力沿涡轮-导轮下降的更快,导轮叶片的整体压强显著低于i=0时;在泄漏区压力分布图中,导轮两侧泄漏区左侧压力依旧大于右侧压力;与泵轮相关的左侧外泄漏区,压力变化规律与i=0大致相同,此时压力下降更快,压力梯度更加明显。
当i=0.8时,内流场中涡轮入口压力进一步上升,泵轮出口的高压区进一步扩大,导轮整体压力更加低;泄漏区中,导轮两侧泄漏区左侧压力趋于一致;左侧外泄漏区中,压力下降的趋势更加明显。
3 轴向力构成及计算结果分析
3.1 轴向力随速比分布
轴向力计算结果如图7所示,泵轮轴向力的大小随传动比的增加先增大后降低,在传动比i=0.3时达到最大值,泵轮受到轴向力的方向始终为正值,代表着方向始终朝向涡轮,在低传动比0~0.5时泵轮的轴向力变化不大,较为稳定;导轮轴向力的大小随传动比的增加而降低,在传动比较低时整体数值下降幅度不大,在传动比i=0时达到最大值,在传动比大于0.4后轴向力大小迅速降低,在i=0.8达到力最小值,导轮受到的轴向力方向始终为负,即朝向泵轮方向。
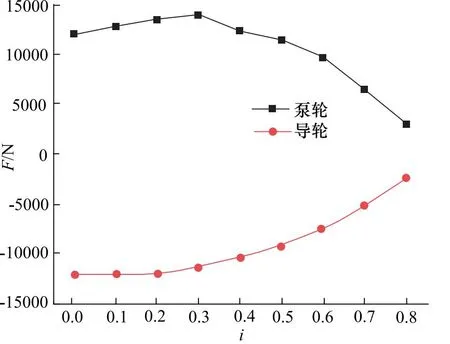
图7 泵轮、导轮轴向力仿真结果图
3.2 泵轮轴向力构成分析
对于泵轮所受轴向力,其包括泵轮叶轮、泵轮毂以及闭锁离合器产生的轴向力,泵轮叶轮包括泵轮叶片与泵轮内外环的壁面。因此用FBy表示液体作用在泵轮叶片上的轴向力、FBh表示液体作用在泵轮内外环壁面的轴向力、FBs表示液体作用在闭锁离合器壁面上的轴向力、FBg表示液体作用在泵轮毂壁面上的轴向力,这些力之和即为泵轮受到的总轴向力。
泵轮各部分流场截面图如图8所示。泵轮叶片产生的轴向力并不是泵轮轴向力的主要组成部分,泵轮毂由于与工作液体接触的表面积小, 所以产生的轴向力数值上与泵轮叶片量级相似,方向上同样与泵轮轴向力相反;泵轮内外环表面由于与工作液体接触面积大,因此其产生的轴向力高,内环的内外表面均在工作液体中,内外表面轴向力抵消大部分,外环内表面积远大于内环表面积,所以外环产生轴向力是泵轮内外环轴向力的主要部分,方向始终为Z轴负方向,数值较大;闭锁离合器总成壁面产生的轴向力方向始终为Z轴正方向,且数值最大,这主要是因为闭锁离合器总成的壁面面积和不平衡面积最大,不平衡面积大多位于泄漏区,这部分区域高压区较多,所以产生的轴向力也最大。
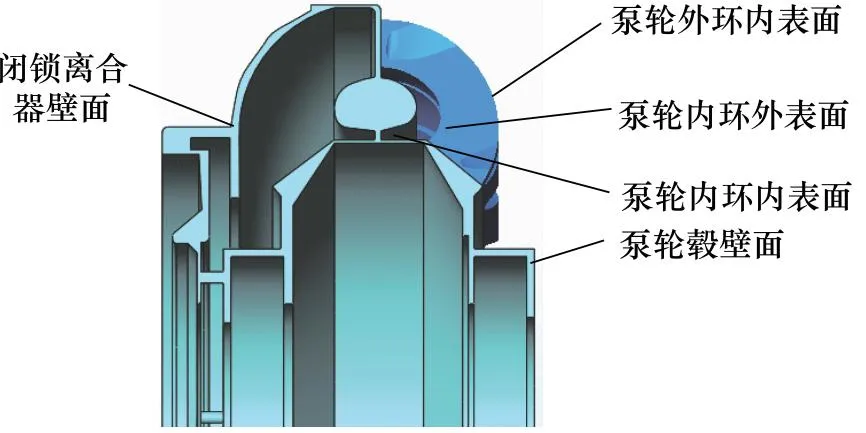
图8 泵轮各部分流场截面图
泵轮各部分轴向力变化如图9所示。由于泵轮始终保持恒定的转速,供油压力变化很小,所以FBy,FBg随传动比的变化不显著;FBs随着传动比增加逐步降低,闭锁离合器总成壁面处流体不属于变矩器循环圆流动部分,这部分工作液体速度大小和压强随传动比变化明显,所以FBs受速比影响显著在i=0.6之后趋于稳定;FBg随传动比增加而先减小后增大,从上图中的压力分布可以得知其外环的平均压力随传动比的增加有先减小后增大的趋势,由于外环的面积大整体压力高,是FBg变化的主要原因。
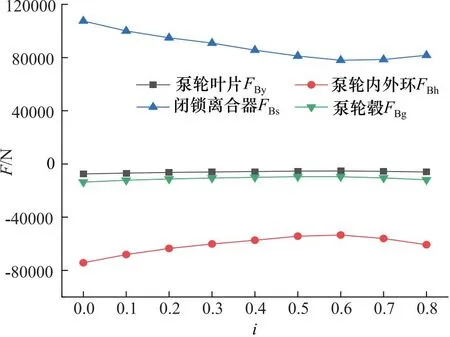
图9 泵轮各部分轴向力变化图
3.3 导轮轴向力构成分析
对于导轮所受轴向力,其包括导轮叶轮、导轮座产生的轴向力,导轮叶轮同样包括导轮叶片与导轮内外环的壁面。因此用FSy表示液体作用在导轮叶片上的轴向力、FSh表示液体作用在导轮内外环壁面的轴向力、FSz1表示液体作用导轮座左侧壁面的轴向力、FSz2表示液体作用在导轮座右侧壁面上的轴向力,以上力总和即为导轮所受轴向力。
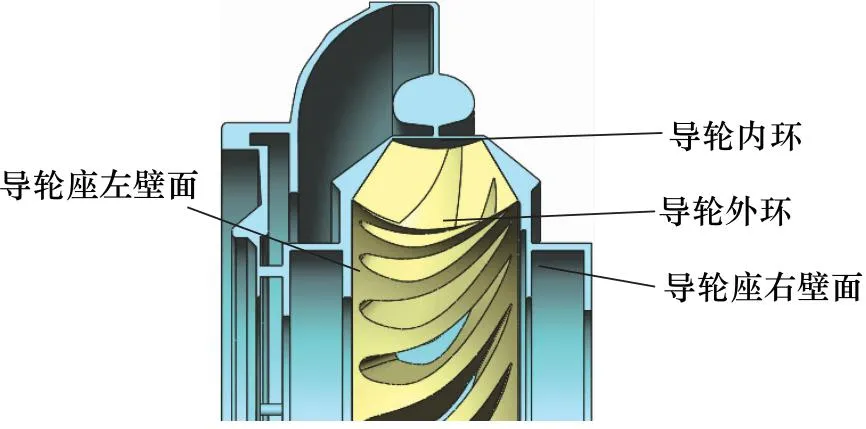
图10 导轮各部分流场截面图
导轮各部分轴向力变化如图11所示,FSy随传动比增加而减小,在i=0处达到最大值,是导轮轴向力变化的主要贡献部分;FSh数值非常小,对导轮轴向力影响不大;FSz1是随着传动比增加而降低的,左壁面受涡轮出口影响较大,传动比越高涡轮出口的压力越小,且由于出油口的压力也降低共同造成了FSz1的变化;FSz2是随着传动比增加先降低后增加,右壁面靠近导轮叶片的上部受导轮出口和泵轮入口影响大,随传动比增加有先降低后增加的趋势。
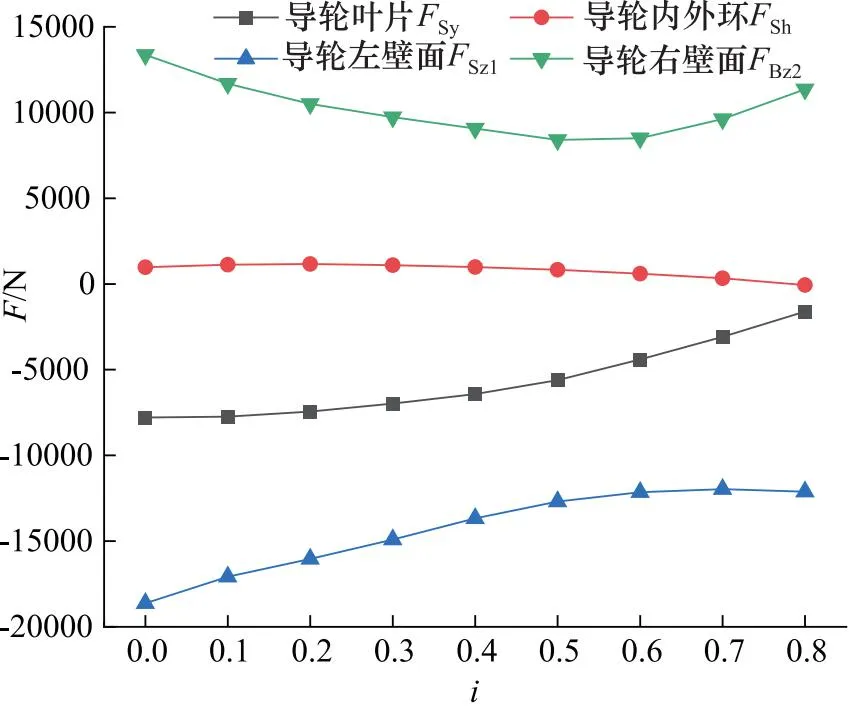
图11 导轮各部分轴向力变化图
4 轴向力测试试验验证
为验证仿真结果,设计了轴向力测试试验台,如图12所示,将轴向力传感器安装在泵轮与导轮之间、涡轮与导轮之间,用于测量泵轮与导轮的轴向力且保证安装方式没有大幅度破坏变矩器的原有流场结构,最大限度保证了变矩器内部结构件的尺寸不发生改变,因此测试时的流场工况可以认为是变矩器正常工作时的工况,轴向力传感器实物图如图13所示。

图12 试验台架图

图13 轴向力传感器实物图
图14是泵轮和导轮轴向力的试验与仿真对比图,可以发现流场仿真能够反应出实际轴向力随工况变化趋势,且最大轴向力预测误差在5%以内。泵轮轴向力随速比先增大后减小;导轮轴向力随速比增大呈下降趋势,在低传动比、大轴向力时仿真与试验测试精度较高。
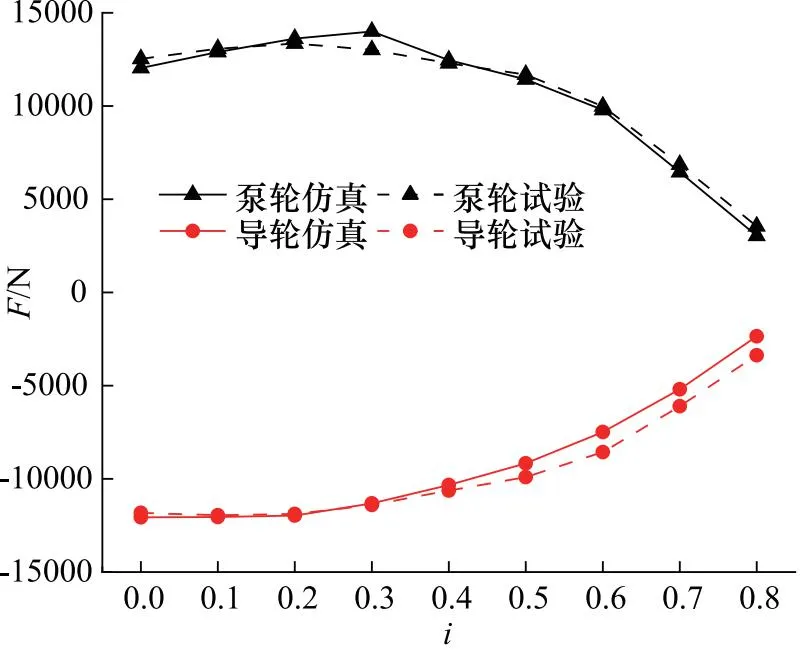
图14 轴向力仿真试验对比图
5 结论
本研究以CFD方法计算出某循环圆直径420 mm的液力变矩器中泵轮和导轮受到的轴向力,分析了其轴向力各自的组成部分, 从不同结构件的角度对轴向力进行了分类,以泵轮转速1800 r/min为例,分析了不同传动比下泵轮、导轮轴向力的变化以及不同结构的不同壁面受力情况,结论如下:
(1) 随着传动比增大,泵轮轴向力是先稳定上升后迅速下降的趋势,在i=0.3工况时泵轮轴向力数值达到最大值,泵轮轴向力最大值为13990 N;随着传动比增大,导轮轴向力逐步降低,在i=0处达到最大值,导轮轴向力最大值为12059.2 N;
(2) 泵轮轴向力中,闭锁离合器所受不平衡压力及泵轮内外环所受轴向力为其最主要的组成部分,叶片和泵轮毂轴向力占比较低。导轮轴向力中,导轮座左、右壁面及导轮叶片所受轴向力占比高,且导轮叶片所受轴向力随速比变化最明显,使得导轮总轴向力随着速比升高呈现降低的趋势;
(3) 泵轮轴向力在低传动比工况下,误差偏大,导轮轴向力在高传动比工况下,仿真数据偏小。数值计算得到的结果中,总的轴向力由各个面的压力分布计算得到,压力分布计算得到的力数值与实际有细微的误差,因此各个面上的计算误差累积形成总的轴向力误差;另一方面,轴向力传感器受温度影响,变矩器试验中,变矩器升温快,测试数据存在误差。最终,测试结果与三维流场计算结果相对比,最大轴向力预测误差低于5%,验证了三维计算结果的准确性。

