考虑参数不确定性的海上风电结构模型修正方法

柳振海，李 刚，刘 博，徐明强，吕 晴，蒋 上

1.(中国电力工程顾问集团有限公司，北京 100120；2.中国海洋大学，山东 青岛 266100 )

0 引言

海上风电作为一种清洁能源，越来越受到世界各国的重视，大力发展海上风电，可优化能源结构，促进经济、社会、环境协调发展。然而，海上风电设施长期服役于复杂的海洋环境中，一旦发生故障或损伤，不仅影响风电运行，也会造成巨大的经济损失，开展结构健康监测势在必行。获取准确的有限元模型是结构健康监测的重要内容，但由于建模误差、参数不确定性等问题，有限元模型不一定能准确反映结构的真实情况，需要对有限元模型进行修正，使得修正后的模型能准确反映真实结构的动力响应特征。

有限元模型修正方法可以分为确定性模型修正和不确定性模型修正。前者将结构参数及响应假设为恒定不变的，修正结果为唯一确定解。但在实际工程设计建设中，结构部件的实际加工组装可能与设计值存在一定误差，导致结构参数的不确定性。因此确定性模型修正得到的最优解只是不确定性模型修正解中的一个特例。随机模型修正是对传统模型修正方法的创新，并考虑到了不确定性因素的影响，利用统计概率分析量化不确定性因素，将不确定模型修正问题转化为均值和标准差的修正问题，从而得到与实际结构动力响应特征一致的有限元模型[1-3]。

由于能够代替复杂的有限元模型分析，代理模型被广泛用于模型修正。许泽伟[4]等提出一种基于多项式混沌展开和KL 散度的随机有限元模型修正方法，以三维桁架为例，对弹性模量和密度的均值和标准差进行修正。冷建成[5]等以某海洋平台结构为研究对象，提出了Kriging模型与多目标遗传算法优化相结合的动力学模型修正方法，实验显示能够显著改善Kriging 模型精度。孙永朋[6]等针对随机模型修正精度和效率低的问题，提出一种基于Kriging 模型和小波包能量谱的随机有限元模型修正方法。丁雅杰[7]等提出一种基于贝叶斯推理的非线性结构模型修正方法，同时考虑激励的随机性，建立了复合随机振动系统的动力可靠度分析方法。

本文针对小样本数据的模型修正提出了一种基于KL 散度的分步型随机模型修正方法，通过数值模拟验证了此方法的有效性。首先采用灵敏度分析法选择待修正参数，通过正交试验生成训练样本，利用有限元模型计算样本响应，从而构造以待修正参数为输入，以频率响应为输出的Kriging 代理模型；利用蒙特卡洛模拟得到初始样本点并计算其响应值，以样本点响应与实测数据的KL 散度构造目标函数，通过多目标优化算法对海上风电结构进行随机模型修正。

1 随机模型修正方法

1.1 Kriging模型

相较于其他响应面模型(如多项式回归、神经网络等)，Kriging 模型在构造过程中只需要较少的样本点，计算成本较低，并且处理非线性数据效果优异[8]，能实现对有限元模型响应较准确预测，更适合处理小样本实测数据的模型修正。

Kriging 模型是一种通过已知样本点信息估计未知试验点信息的无偏估计模型，采用Kriging 代理模型的前提是假设所有数据之间都服从n维正态分布[9]。

已知样本点x= [x1,x2, ...,xm]，xi是n维向量，对应响应为y(x) = [y(x1),y(x2), ...,y(xm)]，由于x服从正态分布，因此y服从均值为μ、协方差C的多维高斯分布。y(x)可以用式(1)表示：

式中：P代表基函数的个数；f(x)=[f1(x)，f2(x)，…，fl(x)，…，fp(x)]∈Rp×p为基函数矩阵；β=[β1,β2…,βl,…,βP]为基函数权重；fT(x)β为线性回归模型，z(x)为服从高斯分布的随机过程；不同变量之间的协方差矩阵C为：

式中：R为数据点之间的协方差矩阵；σ2为方差。

样本点的似然概率为：

式中：n为样本数。

对式(3)取对数：

使得似然概率最大的超参数β，σ2的估计值和为：

对于建立的代理模型，还需要对其进行进一步的验证。本文采用决定系数R2和相对均方误差RMSE评价Kriging 代理模型精度，R2的取值范围为0 ～1，R2值越大，表示预测效果越好，RMSE越趋近于0 表示预测效果越好，其表达式为

1.2 KL散度

KL 散度可以用来度量两个概率分布之间的差异[10]，需要注意的是，KL 散度并不满足对称性，即DKL(P||Q) ≠DKL(Q||P)。假设实测频率与样本频率分别为二维正态分布P和Q，此时DKL(P||Q)为前向KL 散度，主要表现为在任何P(x) ＞ 0 的位置使得Q(x) ＞ 0，即使得Q能够最大程度上覆盖P；DKL(Q||P)为反向KL散度，主要表现为在P(x)趋近于0 时，Q(x)也尽可能趋近于0。

在优化问题中，需要通过迭代优化样本频率Q使得两个分布之间的KL 散度能够尽可能小，从而实现用样本频率Q拟合实测频率P，且实测频率分布往往是多峰分布，前向KL 散度求解得到多个极小值对应的待修正参数的平均值，不能满足优化要求，而采用反向KL 散度则可以确保至少达到一个局部最优解，因此本文采用KL 散度计算实测频率与样本频率分布之间的差异程度。

假设P、Q服从均值为μ0，μ1，协方差矩阵为Σ0，Σ1的高斯分布，则两分布之间的KL散度为：

式中：tr表示矩阵迹；det 表示某矩阵的行列式；k为Σ0的维度。

1.3 目标函数

在优化算法中，目标函数提供了对不同解进行评估和比较的指标，决定了算法的搜索目标，因此选择适当的目标函数对解决实际问题至关重要。本文以待修正参数的均值和方差为修正目标，以实测频率与样本点频率的KL 散度为目标函数，同时对参数的均值和方差进行修正。由于两个分布没有重叠时，KL 散度没有意义，无法进行迭代操作，因此将目标函数分为两个部分：首先通过样本点频率及实测频率的均值、方差构造多目标函数进行优化计算，当两个分布出现重叠时，改用KL 散度为目标函数，具体目标函数构造如下：

式中：nsim为样本响应数量；nobs为实测值数量。

1.4 优化算法

在确定好目标函数后，需要选择合适的优化算法求待修正参数的最优解。NSGA-Ⅱ[11]是目前最常见的多目标优化算法之一，在原始算法的基础上，引入了快速非支配排序、拥挤度等概念，减少了计算的复杂度，并提高了算法效率，其基本思想为：

1)随机生成规模为N 的初始种群Pt，通过非支配排序、选择、交叉、变异，生成子代种群Qt；

2)将初始种群Pt与子代种群Qt合并得到新的种群Rt；

3)进行快速非支配排序，并对每个非支配层的个体进行拥挤度计算，根据非支配关系及个体的拥挤度选择合适的个体组成新的父代种群Pt+1；

4)采用遗传算法生成新的子代种群Qt+1，并将Pt+1与Qt+1合并生成新的种群Rt；

5)依此类推，直到满足程序结束的条件。

2 海上风电结构数值模型

选取一个5 MW 海上风机作为研究对象，风机采用导管架基础，基础深入海底，底部高程为-50.001 m，顶部高程为10.262 m，上部塔筒高度100 m，采用变截面，塔筒底部直径6 m，壁厚0.035 1 m，顶部直径3.87 m，壁厚0.024 7 m，顶部机箱和叶片简化为偏心质量点，共31.452 t。利用ANSYS 建立有限元模型，模型共166 个节点，221 个单元。对其进行模态分析，得到前6 阶频率为：0.490 16 Hz、0.490 28 Hz、1.661 4 Hz、1.661 8 Hz、3.774 2 Hz、3.774 3 Hz，前三阶模态振型如图1 所示。

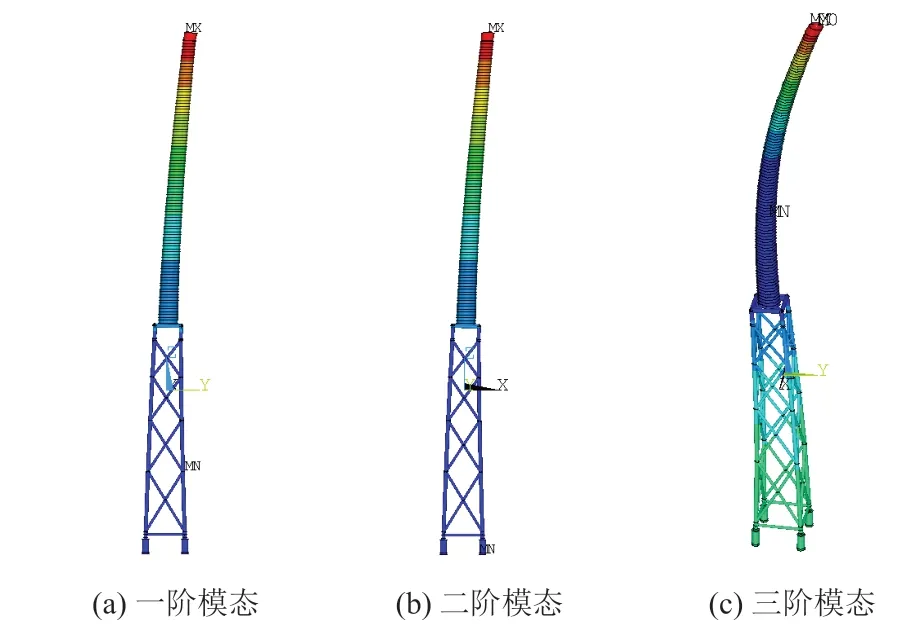
图1 海上风机前三阶模态振型

3 海上风电结构随机有限元模型修正

3.1 修正参数的选择

考虑到海上风机长期受腐蚀、冲刷、温度、湿度等因素影响，其中材料参数选择弹性模量、密度为待选参数，几何参数选择基础腿柱外径、斜撑外径、腿柱壁厚、斜撑壁厚为待选参数。对待选参数进行灵敏度分析，选择高灵敏度修正参数：将各初选参数值增加2%，得到修改后的频率值，计算各阶频率变化率，除以参数变化率即为各参数前两阶频率的灵敏度S，如式(11)所示。

式中：f i为第i阶初始频率，Hz；为参数值增加后的第i阶初始频率，Hz；Pm为初始参数值；Pmc为增加后的参数值。

表1 为修正参数各阶频率灵敏度，由表1可知，在材料参数中，弹性模量与密度灵敏度相差不大，在几何参数中，腿柱外径灵敏度较高。由于采用材料参数可以有效地提高方差修正效果，因此最终弹性模量(E)、密度(Des)及腿柱外径(OL)为待修正参数。假设待修正参数服从高斯分布，根据施工图纸及工程经验确定其初始均值、方差见表2 所列。

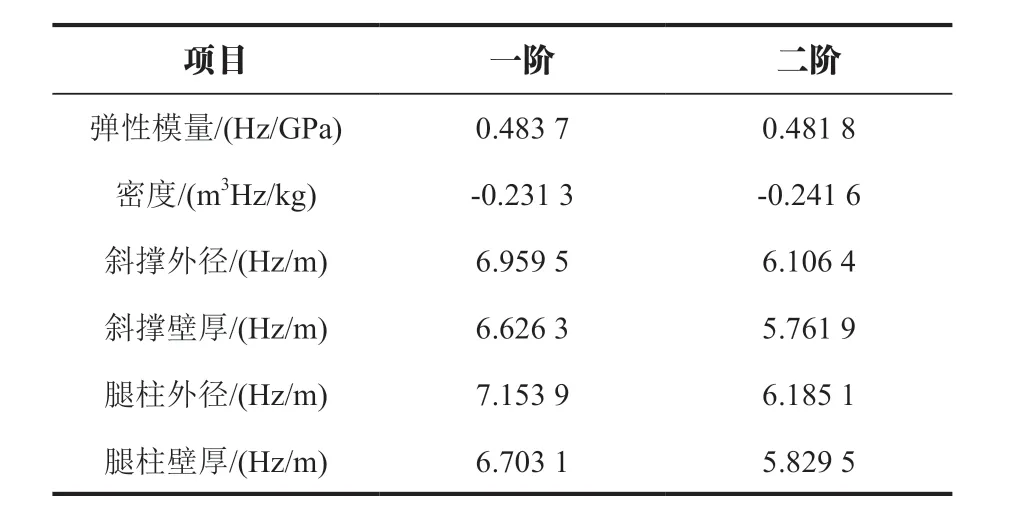
表1 修正参数各阶频率灵敏度

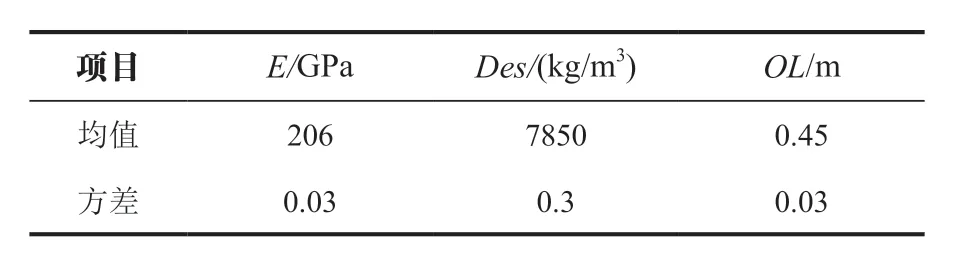
表2 修正参数初始均值与方差

3.2 建立代理模型

根据各参数的初始均值和方差选择95%置信区间为修正参数取值范围，即：弹性模量取值范围为[205.941，206.059]，密度取值范围为[7 849.4，7 850.6]，腿柱外径取值区间为[1.191，1.309]。通过正交试验设计选择，取三因素五水平共25 组设计样本参数，见表3 所列，将样本参数代入有限元模型中计算得到前两阶频率，由此构建Kriging 模型。

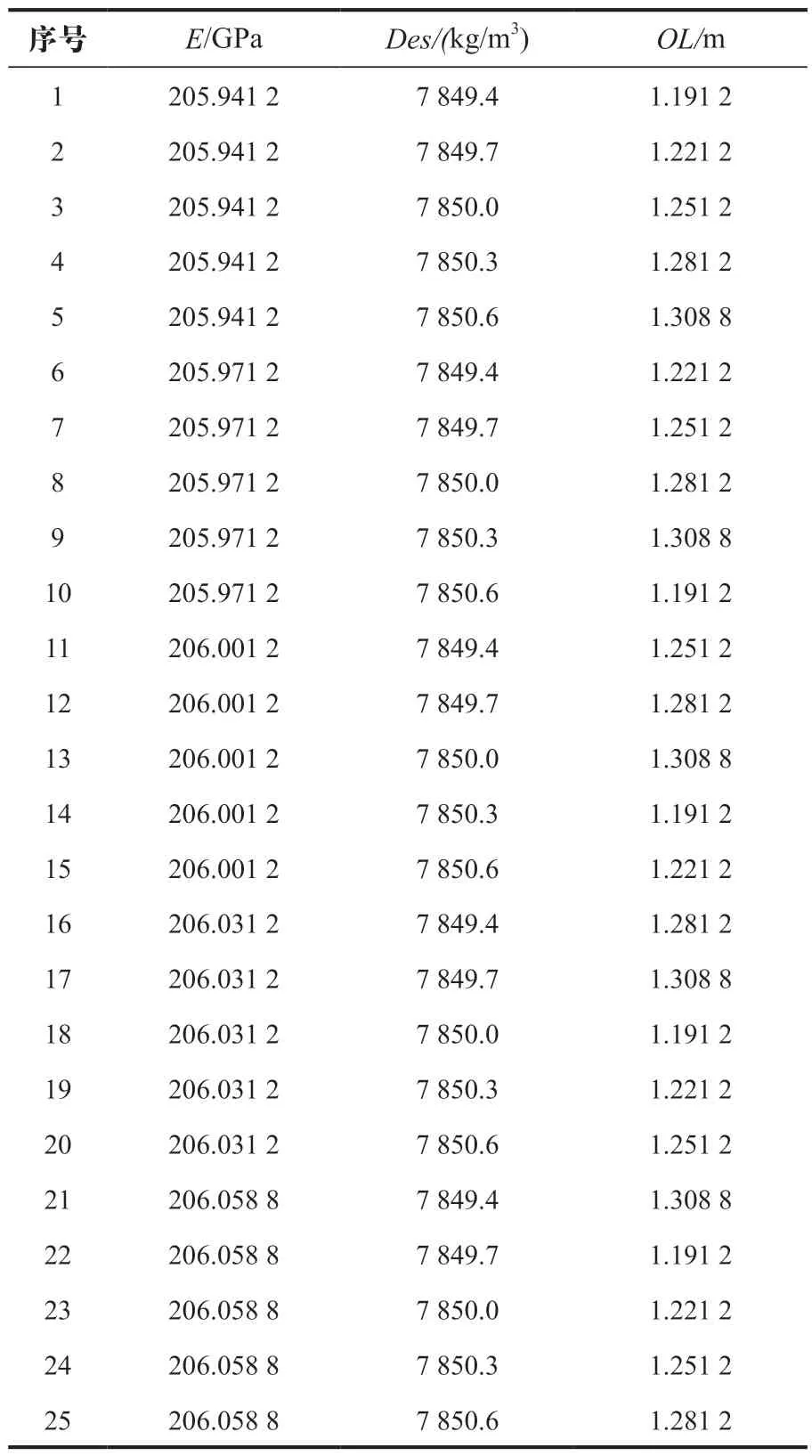
表3 正交试验设计样本

采用相对均方误差RMSE与决定系数R2对建立的Kriging 代理模型进行有效性评价，计算结果见表4 所列，证明构造的Kriging 代理模型精度较高，可以代替有限元模型。

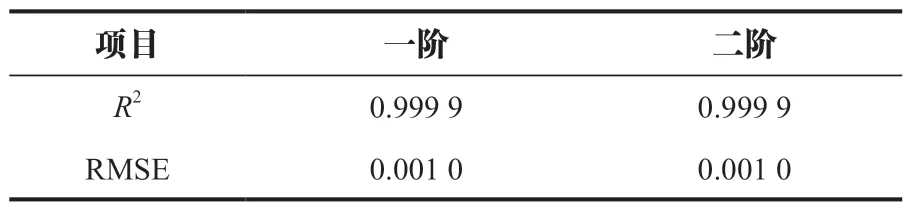
表4 Kriging代理模型有效性评价

3.3 数值模拟

假设有限元模型待修正参数试验值与初始值见表5 所列，对试验值进行蒙特卡洛抽样1 000 次得到样本点，通过Kriging 模型计算得到样本点前两阶频率响应作为实测数据。首先采用实测数据与每次迭代生成的随机样本频率的均值和方差构造多目标函数，随后利用NSGA-Ⅱ多目标优化算法进行求解，得到结构待修正参数的修正值，见表5 所列。

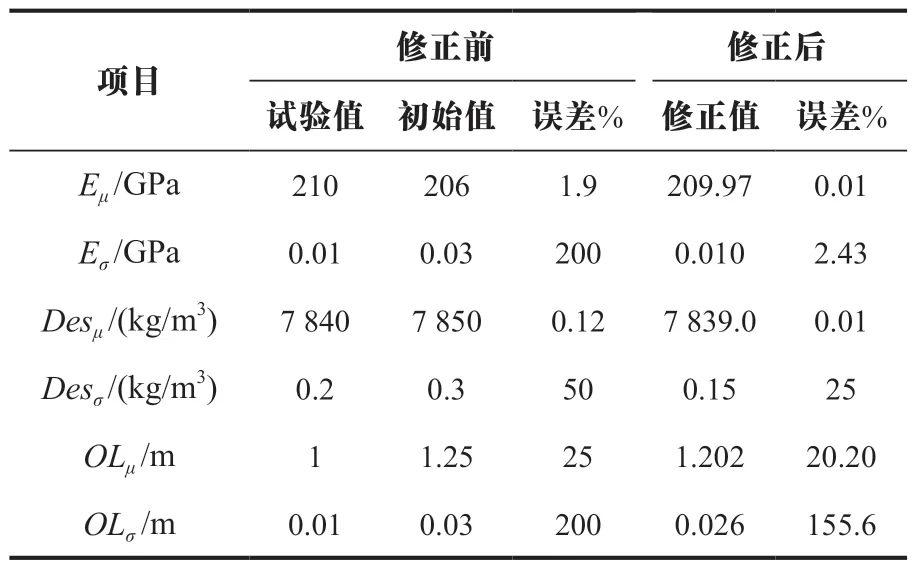
表5 参数修正前后误差

表5 中标准差是实测数据与其平均数离差平方的算术平均数的平方根，反映实测数据的离散程度，误差是试验值与初始值之间的差异。根据修正参数最优解，通过构造的Kriging 模型进行计算，得到修正后有限元模型前五阶频率的均值和标准差，与初始值和试验值进行比较，见表6、表7 所列，修正前后频率均值的最大误差由68.59%降低为0.1%，标准差的最大误差由212.82%降低为17.29%，且前三阶频率标准差最大误差为0.48%，修正结果表明本文方法有效。

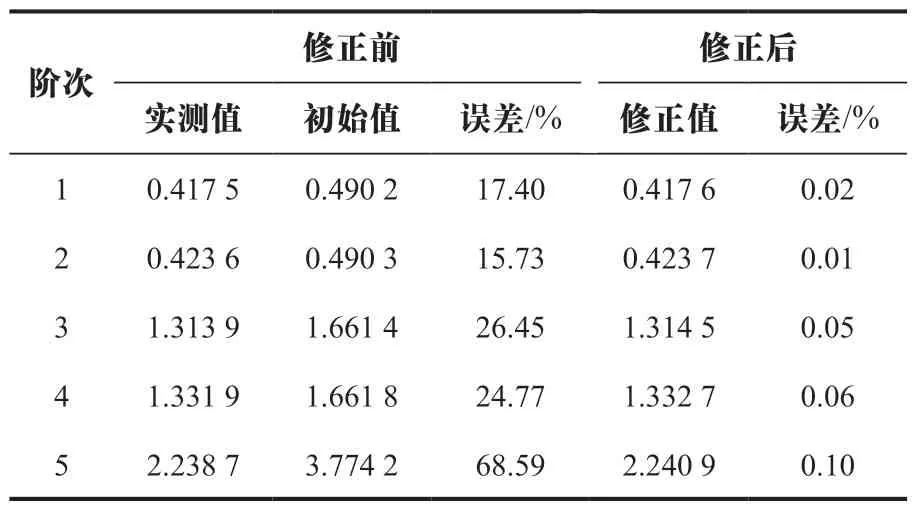
表6 修正前后频率均值

绘制修正前后模型与试验模型频率置信椭圆如图2 所示，可以看出，修正前实测值与初始值频率置信椭圆大小与中心点位置有明显差异，修正后实测值与修正值的频率置信椭圆的大小、中心点、倾斜方向几乎完全相同。图3给出了结构前两阶频率修正前后的概率密度曲线，对比可知，修正前实测值曲线与初始值曲线的峰值有明显差异，两条曲线重合程度较低。修正后的实测值与修正值概率密度曲线形状相似且几乎完全吻合。进一步验证了本文所提修正方法的有效性。

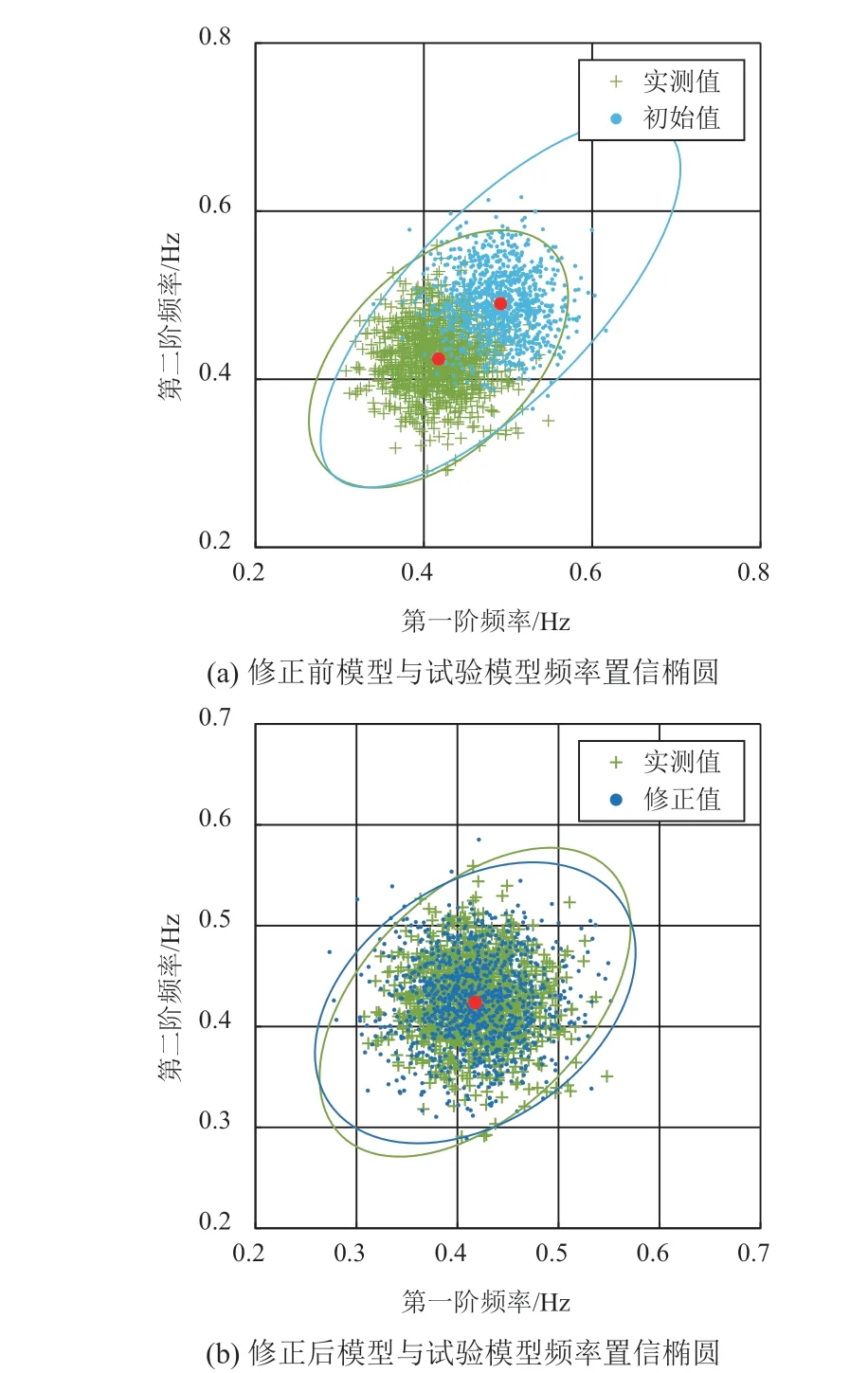
图2 修正前后模型与试验模型频率置信椭圆

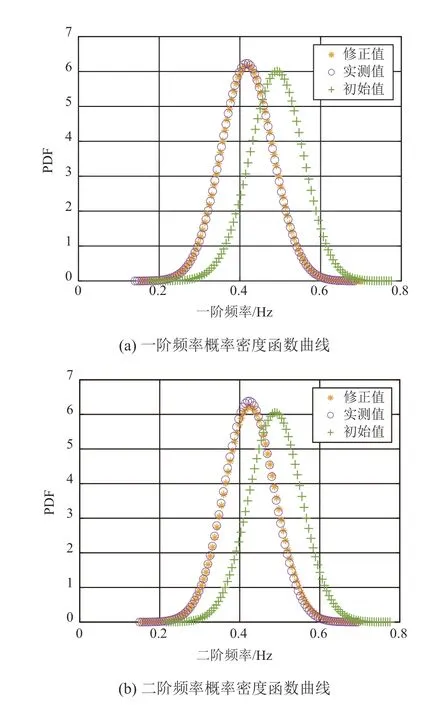
图3 修正前后频率概率密度曲线

4 结语

考虑到参数随机不确定对结构响应分布的影响以及KL 散度在不确定性度量的优势，本文采用Kriging 模型代替有限元模型进行计算，并通过灵敏度分析法选择合适的待修正参数，提高了代理模型的精度和修正效率。同时，选择能够度量两个分布之间差距的KL 散度构造目标函数，以海上风机频率均值和标准差为修正目标进行随机模型修正，修正后的有限元模型响应与实际结构响应高度吻合。结果表明，基于Kriging 模型和KL 散度的随机模型修正方法可以用于小样本实测数据的海上风电结构随机模型修正，且修正效果显著。开展风电实验模型修正将是未来进行的工作。