修正共轭梯度算法求解四元数Sylvester张量方程

胡晶晶 ,柯艺芬 ,马昌凤

(1.福建师范大学数学与统计学院,福建 福州 350117;2.福建师范大学分析数学及应用教育部重点实验室,福建 福州 350117;3.福建省应用数学中心,福建 福州 350117)

1.引言

四元数经常出现在许多领域,如量子物理、信号处理、彩色图像处理和计算机科学等[1-4].由于四元数域比复数域提供了更多的自由度,因此在处理多维问题时,四元数比实数和复数具有更多的通用性和灵活性.因此,越来越多的学者对四元数的理论性质和计算问题感兴趣,并取得了许多有价值的成果.例如,文[5-6]通过复表示方法获得了四元数矩阵方程AXB+CY D=E和AHXA+BHY B=C的极小范数η-(反)-Hermitian最小二乘解的显示形式.文[7]通过实表示方法推导出了四元数矩阵方程AXB+CY D=E的η-Hermitian和η-反-Hermitian解.文[8]建立了一种有效的迭代方法去获得四元数矩阵方程AXB+CY D=E的极小范数η-Hermitian和η-反-Hermitian最小二乘解.文[9]考虑了四元数Sylvester张量方程的最小二乘问题,通过求解其等价形式从而得到了四元数Sylvester张量方程的最小二乘解.

本文采用以下符号: R表示实数集,Rn表示n维实向量空间,Rn×n表示n×n阶实矩阵集合,表示N阶I1×I2×···×IN维实张量的集合,Q表示四元数体,Qn×n表示n×n阶四元数矩阵集合,表示N阶I1×I2×···×IN维四元数张量集合;AT表示矩阵A的转置,R(A)表示矩阵A的列空间.

2.预备知识

定义2.1四元数a可以表示为

其中as ∈R,s=1,2,3,4,且i,j,k满足

对于两个四元数a=a1+a2i+a3j+a4k∈Q和b=b1+b2i+b3j+b4k∈Q,它们的乘积定义为

定义2.2四元数张量A可以表示为

其中As ∈,s=1,2,3,4.四元数张量A的共轭可被定义为

类似地,对于四元数矩阵A,有着相似的表示.

例2.1[10]张量A ∈R3×4×2的两个正面切片分别为

张量A沿模-1展开成矩阵A(1),其中

定义2.4[11]对于张量A ∈,算子‘vec’将张量的列叠加成一个向量,定义vec(A)=vec(A(1)),其中A(1)是张量A沿模-1的展开矩阵.

例2.2若张量A ∈R3×4×2如例2.1所示,则vec(A)=[1,2,···,24]T.

证四元数Sylvester张量方程(2.2)可写作

将式(2.7)和式(2.8)代入式(2.6),根据定义2.7,四元数张量相等意味着实部和虚部分别对应相等,从而可得方程组(2.3).

进一步,根据Kronecker积和向量化算子,从而可得线性方程组(2.4).

注2.1值得注意的是当线性方程组(2.4)的系数矩阵规模非常大时,寻找其数值解将面临很大的计算挑战.文[12]表明,基于张量格式的算法总体上比经典形式的算法效率更高.下面我们将构造一类基于张量形式的高效迭代算法求解方程组(2.3),并建立迭代算法的收敛结果.

注2.2记

3.全局收敛性

本节主要考虑四元数张量方程(2.2)的求解.利用定理2.1,可以将四元数张量方程转化为实张量方程组(2.3),考虑用张量形式的修正共轭梯度(Modify Conjugate Gradient,MCG)算法求解(2.3),从而得到方程(2.2)的解.

为了方便起见,我们引入下列线性算子:

从而四元数Sylvester张量方程(2.2)可写成

步4 置k:=k+1,返回步2.

定理3.1假设序列{Rs(k)}和{Qt(k)}(s=1,2,3,4,t=1,2,3,4)由算法3.1生成,则下列等式成立

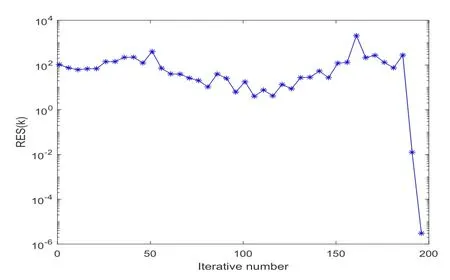
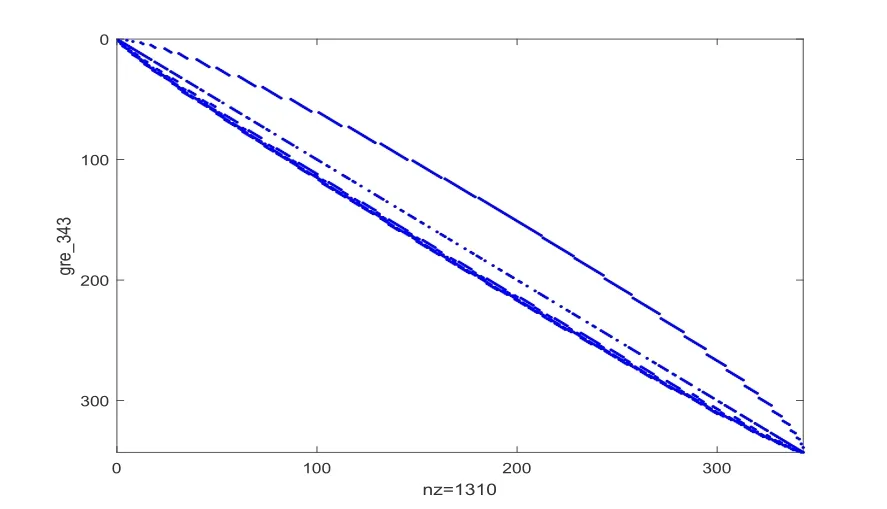
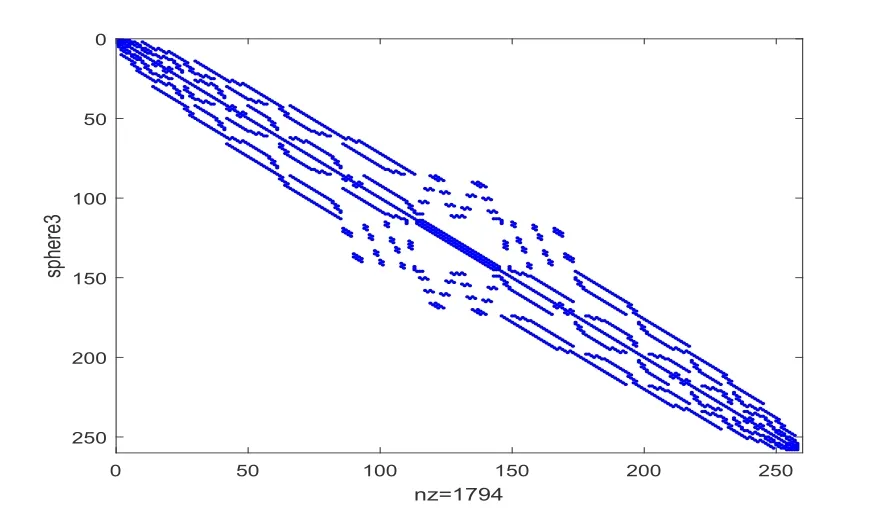
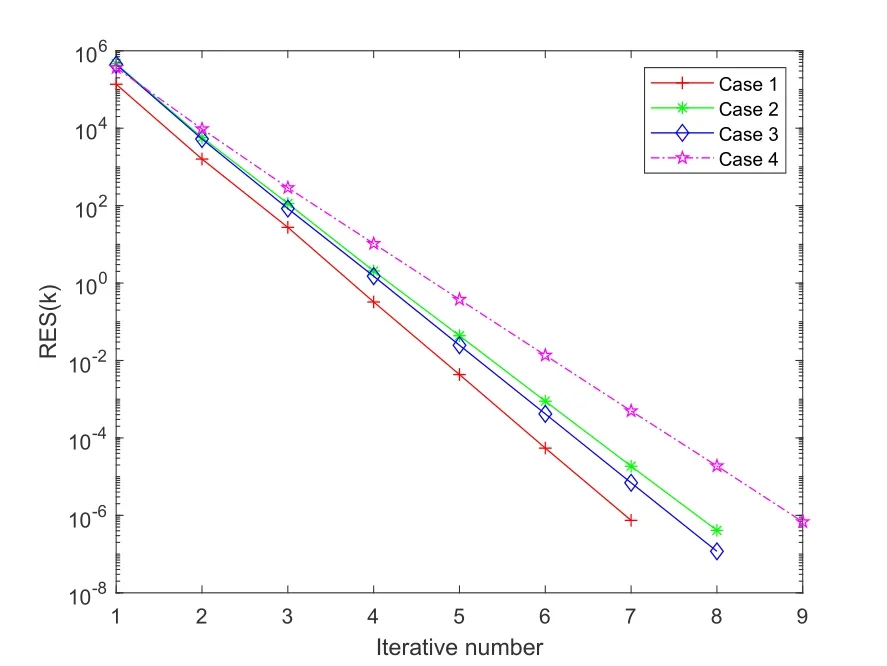
证首先,我们证明式(3.3)和式(3.4)对于0≤u

从而,当k=1时,式(3.3)和式(3.4)成立.

现假设式(3.3)和式(3.4)对于k=l成立.对于k=l+1,根据算法3.1和式(3.2),我们有

最后,我们证明当u

从而,当k=l+1时,式(3.3)和式(3.4)也成立,则对所有的0≤uv时,式(3.3)和式(3.4)也成立.这样对所有的uv,结论得证.

定理3.2记(t=1,2,3,4)为张量方程组(3.1)的解,则对于任给的初始张量Xt(0)(t=1,2,3,4),由算法3.1生成的序列{Rs(k)}和{Qt(k)}(s=1,2,3,4,t=1,2,3,4)满足

证用数学归纳法.当k=0时,有

假设当k=l(l ≥1)时,式(3.5)成立.对于k=l+1,我们可得

从而当k=l+1时,式(3.5)成立.由数学归纳法可得,式(3.5)对所有的k=0,1,2,···都成立.□

定理3.3若实张量方程组(3.1)是相容的,对任意的初始张量[X1(0),X2(0),X3(0),X4(0)],在不计舍入误差的情况下,其精确解可通过算法3.1在有限迭代步内获得.

通过算法3.1可得到Xt(4I)和Rs(4I),令R(k)=diag{R1(k)(1),R2(k)(1),R3(k)(1),R4(k)(1)},k=0,1,2,···,4I-1,其中Rs(k)(1)表示张量Rs(k)(s=1,2,3,4)沿模-1的展开矩阵,根据定理3.1,有

则R(0),R(1),···,R(4I-1)可构成如下线性空间的一组正交基,

根据定理3.1,有

故Rs(4I)=O.则[X1(4I),X2(4I),X3(4I),X4(4I)]是实张量方程组(3.1)的解.

4.极小范数解

引理4.1[13]若A ∈Rm×n,b ∈Rm,线性方程组Ax=b有解x∗且x∗∈R(AT),则x∗是Ax=b的唯一极小范数解.

定理4.1若实张量方程组(3.1)是相容的,如果选择初始张量为

由于线性方程组(2.4)和实张量方程组(3.1)等价,根据引理4.1可得x∗为(2.4)的唯一极小范数解,从而由算法3.1生成的解(t=1,2,3,4)是实张量方程组(3.1)的唯一极小Frobenius范数解.

5.数值实验

为了验证本文算法的可行性,本节通过三个例子来说明所提出算法的效果.所有的程序都是基于Bader和Kolda[14]开发的MATLAB张量工具箱,实验中,选取N=3,当满足

迭代终止.所有算法均在带有MATLAB R2018a的个人PC机上运行.此外,定义残差范数

考虑初始张量Xt(0)=O(t=1,2,3,4),当满足式(5.1)时迭代终止.根据算法3.1,我们可获得式(5.2)的极小Frobenius范数解,数值结果如图1所示.

图1 例5.1的数值结果

例5.2考虑四元数Sylvester张量方程(5.2),设

令精确解

从而可得式(5.2)的右端项张量C.在这个例子中,张量方程(5.2)是相容的,通过选择初始张量Xt(0)=O(t=1,2,3,4),对于n=10时,执行算法3.1得到的收敛曲线如图2所示.

图2 例5.2的数值结果

下面的例子通过求解稀疏四元数Sylvester张量方程来检测算法3.1的有效性.

例5.3考虑四元数Sylvester张量方程

其中系数矩阵满足

与Ahmadi-Asl和Beik[8]工作稍有不同,我们考虑以下四种情况:

情况1A11=S1,A12=pivtol,A21=S2,A13=S3,A14=S4;

情况2A11=S1,A12=gre-343,A21=S2,A13=S3,A14=S4;

情况3A11=S1,A12=mesh3em5,A21=S2,A13=S3,A14=S4;

情况4A11=S1,A12=sphere3,A21=S2,A13=S3,A14=S4.

测试矩阵来自于Davis收集的矩阵[15].数据来源于HB(Harwell-Boeing) group.在这个例子中出现的这四种测试矩阵(pivtol,gre-343,mesh3em5和sphere3)经常出现在统计、有向加权图和结构问题中.这些矩阵的稀疏结构如图5.1-5.4所示,测试矩阵的性质见表5.1,其中‘nz’表示非零项的个数.需要注意的是,这里的稀疏矩阵的阶数较大,因此四元数Sylvester张量方程(5.3)的解的维数非常大.令

表5.1 例5.3测试矩阵的性质

图5.1 第一个测试矩阵的稀疏结构

图5.2 第二个测试矩阵的稀疏结构

图5.3 第三个测试矩阵的稀疏结构

图5.4 第四个测试矩阵的稀疏结构

其中对于情况1-4,n分别取为102,343,289和258作为其精确解.

通过选择初始张量Xt(0)=O,应用算法3.1去求解张量方程(5.3),当满足式(5.1)时迭代终止,相应的收敛结果如图5.5所示,结果证实了算法3.1的收敛性,可以看出残差范数是显著下降的.因此,算法3.1对于求解稀疏张量方程是有效的.

图5.5 例5.3的收敛结果

6.结论

本文通过将四元数Sylvester张量方程等价地转化为实数域上的张量方程组并引入线性算子,构造了基于张量形式的修正共轭梯度算法求其等价形式.理论分析表明对任给的初始张量,由算法3.1生成的迭代序列在不计舍入误差的情况下,可在有限迭代步内收敛到方程组的精确解.进一步,通过选择特殊类型的初始张量,可获得唯一极小Frobenius范数解.最后,数值例子证明了该算法的有效性.