带有负顾客和启动时间的排队系统最优策略分析

何柳青,田瑞玲

(燕山大学理学院,河北 秦皇岛 066004)

1.引言

现实中存在许多系统被干扰的情况,如操作失误致使生产系统中生产进度受到制约,木马入侵使得计算机系统崩溃,外部撞击使得车辆系统故障等.以上举例中的干扰信息被称之为负顾客,它的到达不仅可以使得系统故障,还可以在系统忙期时产生抵消的作用.自20世纪90年代Gelenbe[1]首次提出关于负顾客的排队模型起,关于负顾客的研究不断涌现.尤其近些年从经济学角度分析负顾客排队模型逐渐成为了热点.在经济学和博弈论的背景下,顾客有决策权,可根据自身掌握的有关系统的信息做出进队还是止步的决定,考虑顾客的行为使得研究更有实用性.Lee[2]研究了带有负顾客的排队系统在几乎不可视和完全不可视两种情形下的顾客止步和最优定价策略.WANG等[3]研究了带有负顾客的重试排队系统,讨论了完全可视和几乎不可视两种情形下的纳什均衡策略和社会最优问题.Panda和Goswami[4]考虑了带有负顾客和工作休假的M/M/1排队系统,并且讨论了四种信息水平下的均衡策略行为.ZHANG和WANG[5]分析了带有负顾客和N策略的M/M/1排队系统,并讨论了纳什均衡策略.

在实际中,许多系统由闲期转入忙期需要一段准备时间,即启动时间.比如设备开机过程中要经历供电和初始化等一系列操作,又比如发动机接受到发动指令时需经过转动曲轴并使其达到一定的转速等操作才能完成发动,这些例子中的准备时间都可以抽象为启动时间.Burnetas和Economou[6]分析了带有启动时间的M/M/1排队系统在完全可视,几乎可视,几乎不可视和完全不可视四种信息水平下的均衡止步策略.SUN,GUO和TIAN[7]则进一步考虑了带有启动期和关闭期的排队系统,并分析了顾客的进队阈值策略.CHEN和ZHOU[8]考虑了带有启动时间和故障的排队系统中顾客的均衡止步策略.在此基础上,CHANG和WANG[9]将其推广到重试排队系统中,分析了具有启动时间和故障的重试队列.YUE等[10]研究了具有启动时间和单重休假的M/M/1排队系统,分析了完全可视和完全不可视两种情形下的顾客止步策略.ZHOU等[11]研究了带有启动时间和N 策略的重试排队系统的顾客的均衡止步行为.关于排队经济策略的分析还可以参阅文[12-14].

参阅已有的文献,发现负顾客和启动时间受到了人们的普遍关注,因此本文展开了对结合负顾客和启动时间的排队模型的相关研究.负顾客到达时,会使得服务台故障,并且抵消正在接受服务的顾客.而启动时间的引入,使得空闲服务台及时去休假,不仅能在某种程度上降低服务台故障的风险,还能起到节能的作用.此模型在计算机系统、通信系统、车辆工程等领域有着普遍的应用.比如在计算机领域中,当按下电源开关时,计算机会经历供电、BIOS自检、系统引导等一系列的流程才能完成启动进行工作.在工作过程中,可能会遭遇木马入侵,使得系统文件受到损害,正在进行的操作被迫终止.当受损的系统文件完成备份以后,计算机将恢复工作状态.鉴于其实用性,本文对其做出研究分析.在本文中,我们考虑具有启动时间和负顾客的排队系统中的顾客策略行为,更贴近实际问题,也丰富了现有的排队内容.利用概率母函数法计算系统的重要性能指标,然后基于收益-成本结构讨论顾客的均衡策略和社会最优策略.最后通过数值分析考察社会最优进入策略和最优社会福利关于一些参数的敏感性.

2.模型描述

考虑一个带有负顾客和启动时间的M/M/1排队系统.到达系统的顾客有两种,正顾客和负顾客,分别服从参数为λ和α的泊松流.正顾客的到达是为了寻求服务,而当负顾客到达时,不仅会抵消正在接受服务的正顾客,还会使得服务台故障.发生故障的服务台即刻被送去维修,维修时间服从参数为β的指数分布.故障时顾客不会进入系统.当系统为空时,服务台会立即关闭.若有新顾客到达,服务台会立即启动.启动时间服从参数为θ的指数分布.服务时间服从参数为µ的指数分布,服务顺序是先到先服务.假设顾客到达的间隔时间,负顾客到达的间隔时间,服务时间,维修时间,启动时间是相互独立的.

定义(N(t),I(t))为时刻t系统的状态,其中N(t)表示系统中顾客的数量,I(t)表示服务台状态(0:故障;1:繁忙;2: 启动).过程{(N(t),I(t)),t ≥0}是状态空间Ω={(n,i),n ≥0,i=0,1,2}的连续时间马尔科夫链.

本文感兴趣的是顾客到达系统时的策略行为,为了量化此过程,引入线性“收益-成本”结构,每个顾客在服务完成后,会获得回报R,同时也要支付成本,每单位时间的逗留成本是C.假设顾客是风险中立的,期望最大化自己的收益,并且一旦做出决定不得后悔.

顾客到达系统时,会根据其了解的有关系统状态的信息来决定进队的策略.本文考虑了不可视的两种情形: 1)几乎不可视: 到达顾客被告知服务台的状态信息;2)完全不可视: 到达顾客对系统的状态一无所知.

3.几乎不可视情形

本节研究几乎不可视情形下顾客的均衡进入概率.在几乎不可视情形下,到达的顾客掌握了服务台的状态信息,因此假设顾客遵循混合进队策略(q1,q2),q1和q2分别代表服务台状态为1和2的顾客进入概率,实际到达率为λqi.状态转移图如图3.1所示.

定义pn,i为系统的稳态概率,相应的母函数定义如下

其中|z|≤1.

定理3.1在带有负顾客和启动时间的几乎不可视M/M/1排队系统中,假设<1,服务台状态i=0,1,2的稳态概率分别如下

证系统的平衡方程如下

将式(3.15)和(3.8)代入(3.16)可得

将式(3.14)代入(3.17)可得

将式(3.18)代入(3.15)可得

观察式(3.1),(3.2),(3.3)和(3.7),容易得出此排队系统的稳态条件为<1.

接下来,计算顾客在不同状态下进入系统的平均逗留时间.当标记顾客进入系统发现自己位于系统中第j个位置,且服务台状态为i时,其平均逗留时间为T(j,i),可以得到如下定理.

定理3.2对于带有负顾客和启动时间的几乎不可视M/M/1排队系统,标记顾客到达时发现自己处于系统中第j个位置,且服务台状态为i(i=1,2)的平均逗留时间分别如下

证通过分析,可以得到如下等式

将式(3.25)代入式(3.23),可得

由式(3.22),可得

利用式(3.24),可得式(3.21).

定理3.3对于带有负顾客和启动时间的几乎不可视M/M/1排队系统,一名标记顾客到达时发现服务台状态为i(i=1,2)并选择进入系统的平均逗留时间分别如下

定理3.4对于带有负顾客和启动时间的几乎不可视M/M/1排队系统,服务台处在启动期和忙期(i=1,2)时,顾客均衡进入概率有以下三种情况

证根据线性“收益-成本”结构,可得服务台处于启动期时的平均剩余效用

求式(3.31)对q2的一阶导,可得

容易看出U′2(q2)<0,U2(q2)是关于q2∈[0,1]的减函数.分以下三种情形讨论

服务台处于忙期时的平均剩余效用为U1(q1,q2),其函数表达式如下

U1(q1,q2)是关于q2和q1的函数,上面已经给出了的结果,因此它现在只与q1有关,求U1(q1)关于q1的一阶导,可得

容易看出U′1(q1)<0,因此U1(q1)是关于q1∈[0,1]的减函数,分以下几种情形讨论

前面讨论了顾客的均衡进队策略,每个客户都希望获得最大的平均剩余效用.但从整体来看,这些行为决策不一定是最优的.因此,进一步考虑社会福利,把所有顾客视为一个整体来讨论.Sau(q1,q2)表示几乎不可视情形下的社会福利,表达式如下

其中,P1(1)和P2(1)由定理3.1可得,W1(q1,q2)和W2(q2)由定理3.2可得.

从图3.2中可以看出, Sau(q1,q2)随着q1和q2的增大呈现先增大后减小的趋势. 这是因为当q1和q2较小时, 系统中的顾客也较少, 此时顾客需要支付的等待成本就小, 社会福利增大. 随着q1和q2的增大, 进入系统的顾客越来越多, 系统变得拥挤, 需要支付的等待成本增大, 社会福利减小. 从图中还可以得知, 使Sau(q1,q2)取得最大值的解为然而根据定理3.4可以得到此时的均衡解为很明显最优解和均衡解是不一致的, 这印证了个体均衡和社会最优的差异性. 个体均衡的决策背离了社会最优的决策, 这是由于每个个体为了追求自身效用的最大化导致系统拥挤或否, 使得整体的社会福利减少. 社会管理者可以通过征收入场费或者给予补贴来消除二者之间的差距.

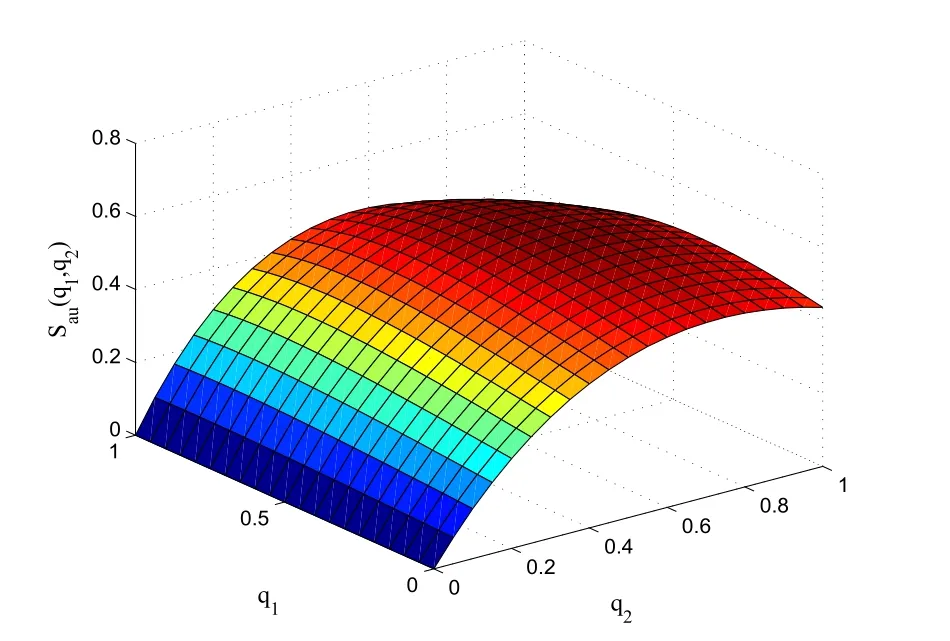
图3.2 Sau(q1,q2)关于q1和q2的变化(λ=1,µ=2.5,θ=2,α=0.2,β=1,R=5,C=4)

本文接下来将讨论社会福利, 引入遗传算法求得最优解并给出一些数值结果. 借助遗传算法去求最优的社会福利Sau(,)以及最优进队概率和. 下面介绍遗传算法的步骤.

步1 首先通过随机方式产生若干由确定长度编码的初始群体;

步2 借助适应度函数对每个个体进行评价,通过轮盘法选择优秀个体参与遗传操作,淘汰劣质个体;

步3 经遗传操作(复制,交叉,变异)的个体集合形成新一代种群,重复步骤2,直到满足停止准则;

步4 将后代中表现最好的个体作为遗传算法的结果.

在遗传算法中,需要明确种群中个体数目(pop),编码方式,交叉概率(pc),变异概率(pm),选择个体的方法,终止运行的条件.在本文中,我们设置pop=200,pc=0.9,pm=0.1,采用十进制编码方式,轮盘法选择个体,通过每个个体与总体的适应度占比来衡量其优劣,比值越大越不容易被淘汰.当满足迭代次数时停止运行,即iter≥500.

借助遗传算法寻得最优解后,将在文章第5部分进一步做最优解关于参数的敏感性分析.

4.完全不可视情形

本节研究完全不可视情形下顾客的均衡进入概率.在完全不可视情形下,到达顾客既不知道服务台的状态信息,也不知道系统的队长信息,假设他们都以概率q进入,那么实际到达率为λq.状态转移图如图4.1所示.

完全不可视情形相当于几乎不可视情形的一种特殊情形,上一节已经给出了几乎不可视情形下的一些结果,对完全不可视排队系统有着重要的参照意义.令式(3.1)-(3.7)中的q1=q2=q,可以得到以下的结果.

定理4.1对于带有负顾客和启动时间的完全不可视M/M/1排队系统,假设<1,服务台状态i(i=0,1,2)的稳态概率分别如下

定理4.2对于带有负顾客和启动时间的完全不可视M/M/1排队系统,一名标记顾客到达并选择进入系统的平均逗留时间为

证根据PASTA性质,系统中顾客的有效到达率为

系统中的平均顾客数为

由Little公式得到顾客的平均逗留时间

定理4.3对于带有负顾客和启动时间的完全不可视M/M/1排队系统,均衡进入概率qe如下

证根据线性“收益-成本”结构,可得顾客的平均剩余效用U(q),表达式如下

求式(4.12)关于q的一阶导,可得

基于函数的单调性,分以下三种情形来讨论

U(q)是关于q的减函数,这表明当q越大时,即其他顾客的进入概率越大时,被标记顾客进入系统并接受服务后获得的平均剩余效用越少,那么被标记顾客进入系统的意愿越低,这种行为被称为拥挤厌恶,由Hassin和Haviv[15]首先提出并命名.此外,还可得知均衡进入概率是稳定的.因为T(q)随着q的增加而增加,平均逗留时间的增加会使得进入系统的顾客减少,因此q的增加会得到遏制,最终趋于平稳.

Sfu(q)表示完全不可视情形下的社会福利,表达式如下

其中,λeff和E(N)由定理4.2可得.

从图4.2中可以看出,随着进入概率的增大,单位时间内系统中的顾客数增大导致社会福利增大,然而过多的顾客逗留在系统中,导致顾客支付的等待成本增大,社会福利减小.同时可以知道,此时使得社会福利最大的解为q∗=0.65.然而根据定理4.1可以得到此时的均衡解为qe=1,最优解和均衡解是存在差异的,个体最优并不能达到社会整体最优,因此社会管理者可以通过征收入场费来遏制顾客的个体决策行为,使二者达成一致.

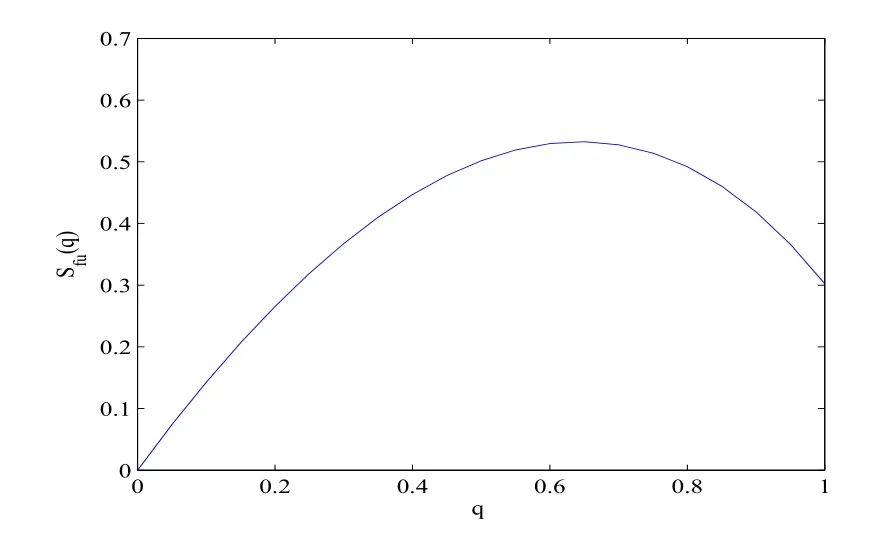
图4.2 Sfu(q)关于q的变化(λ=1,µ=2.5,θ=2,α=0.2,β=1,R=5,C=4)

下文将借助遗传算法去寻找最优的社会福利Sfu(q∗)和最优的进队概率q∗,并进行数值分析.

5.数值分析

本节给出了一些数值例子.数值分析能够直观地展示一些现象,形象地刻画排队模型的实用性.首先,在几乎不可视和完全不可视的情形下,本节分析了系统参数对社会最优进入概率的影响.然后进一步比较两种情形下的最优社会福利,并讨论披露更多的系统信息是否能带来更多的社会福利.

本节给出了一些数值例子. 数值分析能够直观地展示一些现象, 形象地刻画排队模型的实用性. 首先, 在几乎不可视和完全不可视的情形下, 本节分析了系统参数对社会最优进入概率的影响. 然后进一步比较两种情形下的最优社会福利, 并讨论披露更多的系统信息是否能带来更多的社会福利.

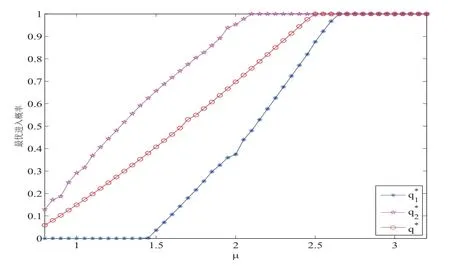
图5.1 最优进入概率(,)和q∗关于µ的变化(λ=1,θ=2,α=0.2,β=1,R=5,C=3)

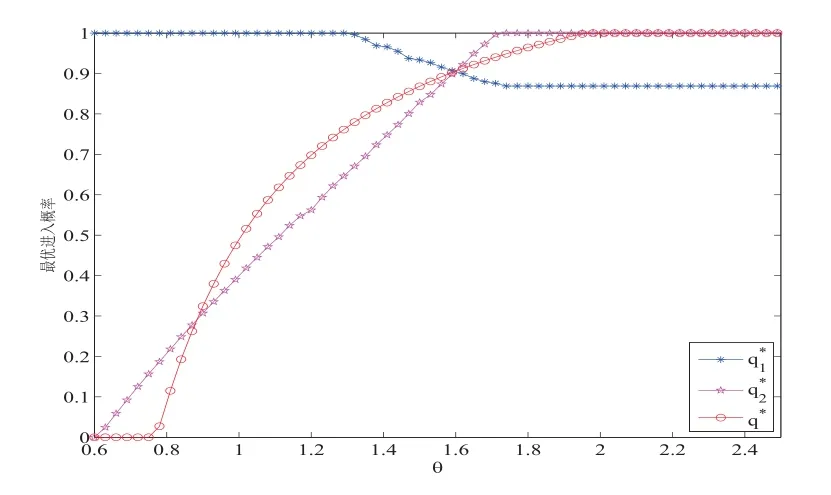
图5.2 最优进入概率(,)和q∗关于θ的变化(λ=1,µ=2.5,α=0.2,β=1,R=5,C=3)

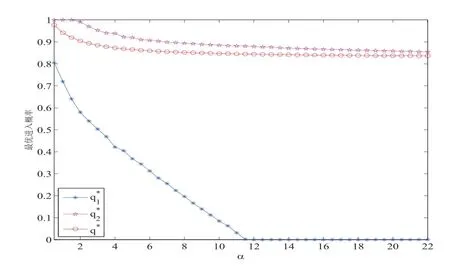
图5.3 最优进入概率(,)和q∗关于α的变化(λ=1,µ=2.5,θ=2,β=1,R=5,C=3)

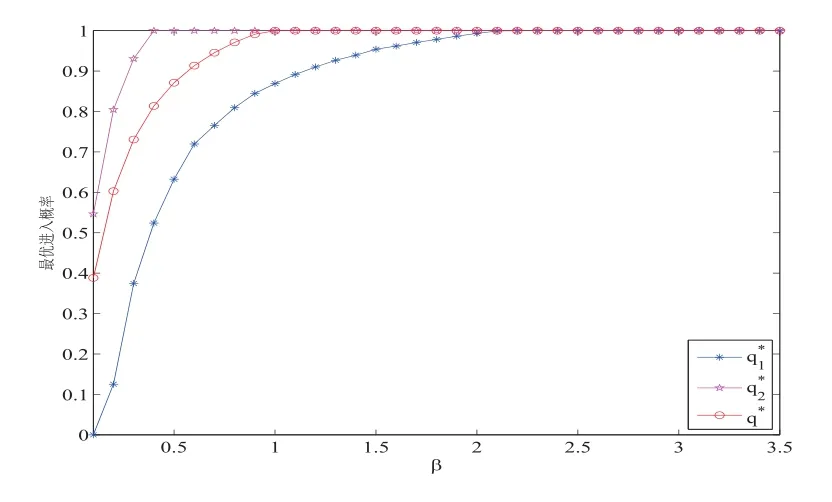
图5.4 最优进入概率(,)和q∗关于β的变化(λ=1,µ=2.5,θ=2,α=0.2,R=5,C=3)

观察图5.1-5.4, 从整体上来看, 不论最优进入概率关于参数的变化是何种走势, q∗大致总是夹在和之间. 也就是说, 在完全不可视的排队系统中, 到达顾客进入系统的概率介于几乎不可视排队系统的两个进入概率之间.

观察图5.1-5.4,从整体上来看,不论最优进入概率关于参数的变化是何种走势,q∗大致总是夹在和之间.也就是说,在完全不可视的排队系统中,到达顾客进入系统的概率介于几乎不可视排队系统的两个进入概率之间.

图5.5-5.8展示了两种信息水平下的最优社会福利. 其中, 从图5.5, 图5.6和图5.8中可以看出,和Sfu(q∗)分别随着参数µ,θ,β 的增加而增加, 这是因为随着服务时间, 启动时间和维修时间的减少, 顾客被服务完成后获得的回报会相应增加, 因此顾客更愿意进入系统, 社会福利随之增加. 从图5.7中可以看出,和Sfu(q∗)随着参数α的增加而减少, 这是因为随着负顾客越来越多的到达, 服务台故障的频率增加, 顾客在系统中等待的成本增加, 因此顾客进入系统的意愿降低, 社会福利减少.

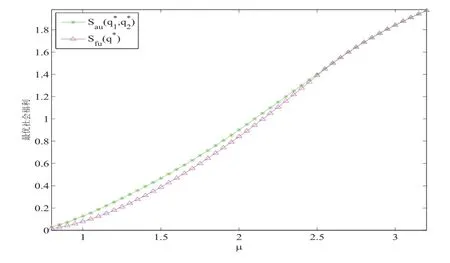
图5.5 最优社会福利Sau(,)和Sfu(q∗)关于µ的变化(λ=1,θ=2,α=0.2,β=1,R=5,C=3)

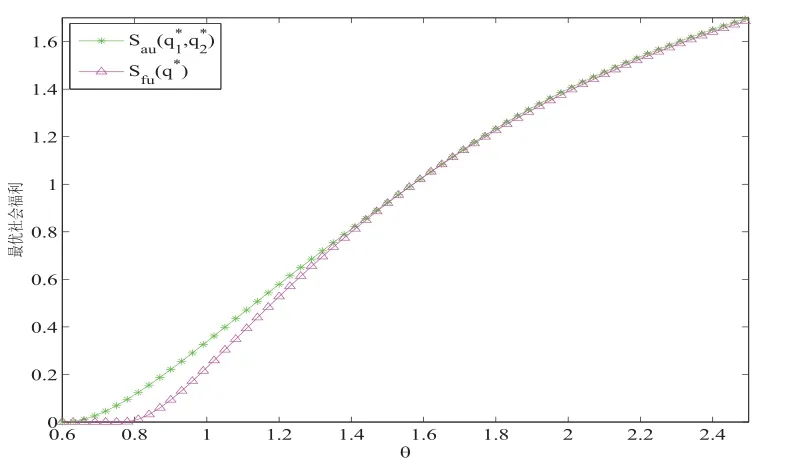
图5.6 最优社会福利Sau(,)和Sfu(q∗)关于θ的变化(λ=1,µ=2.5,α=0.2,β=1,R=5,C=3)

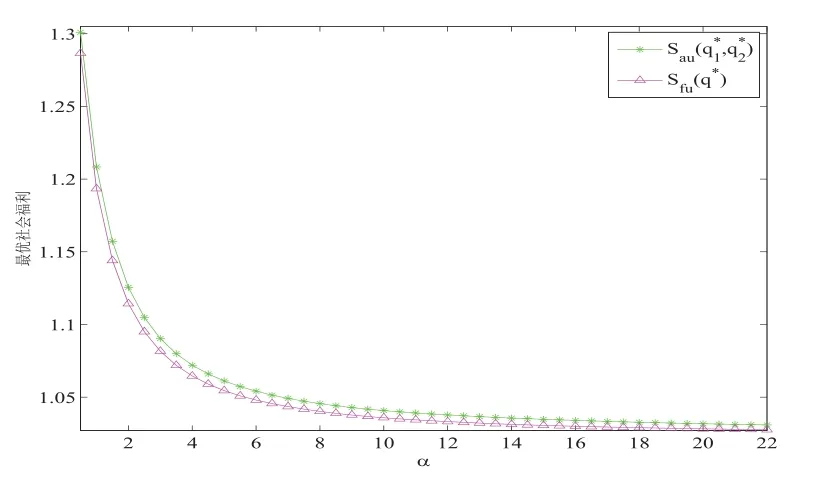
图5.7 最优社会福利Sau(,)和Sfu(q∗)关于α的变化(λ=1,µ=2.5,θ=2,β=1,R=5,C=3)

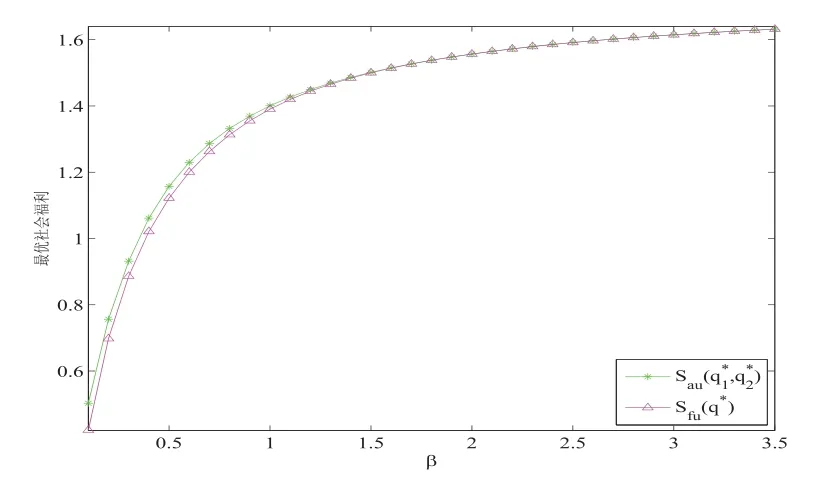
图5.8 最优社会福利Sau(,)和Sfu(q∗)关于β的变化(λ=1,µ=2.5,θ=2,α=0.2,R=5,C=3)

从图5.5-5.8的整体上来看, 不管最优社会福利随着参数如何变化,总是高于Sfu(q∗), 这说明披露服务台状态的信息对社会管理者而言是有益的, 可以获得更高的社会福利. 但是随着参数的增加,和Sfu(q∗)之间的差距越来越小, 逐渐趋于一致.