Finite Integral Transform Solution of the Bending of Moderately Thick Orthotropic Rectangular Plate with Four Sides Free on Winkler Foundation

Ningjin(宁进),Eburilitu(额布日力吐)

(School of Mathematical Sciences, Inner Mongolia University, Hohhot 010021, China)

Abstract: The bending problem of a moderately thick orthotropic rectangular plate(ORP) with four sides free on Winkler foundation is studied by the finite integral transform(FIT) method.Based on the boundary conditions and basic equations of the bending of moderately thick ORP,the analytical bending solution of this plate is obtained by the FIT method and its corresponding inverse transform method.This analytical solution is uniformly applicable to the calculation of bending problems of thin,moderately thick and thick isotropic and orthotropic rectangular plates.Then by specific examples the correctness of the obtained analytical solution is verified.

Key words: Moderately thick orthotropic rectangular plate;Bending;Analytical solution;Finite integral transform method

1.Introduction

In many engineering fields,such as civil engineering,aerospace engineering and mechanical engineering,elastic rectangular plates are common structural form.Therefore,exploring the solutions of bending,buckling and vibration problems of elastic rectangular plates have always been the focus of scholars.At present,many scholars have applied numerical methods to study elastic rectangular plates,such as finite element method[1],finite difference method[2],discrete singular convolution method[3]and spline element method[4].In addition to numerical methods,there are also a few analytical methods for studying the elastic rectangular plates.The representative analytical methods include the inverse or the semi-inverse method[5],the Fourier series method[6],the superposition method[7]and the FIT method[8].Among the above analytic methods,the FIT method is one of the best methods for solving partial differential equations.Compared with the classical inverse method or semi-inverse method,this method is not required to select any trail function in advance and has the advantages of good universality.The FIT method has been applied to solve some practical problems in engineering fields[9-14].Especially,regarding the problems of plates and cylindrical shells,Li’s group has done some very meaningful work by using the FIT method,for example,the bending problem of cylindrical shell panels has been solved in [10],the buckling problems of thin plates have been solved in [11],and the bending problems of rectangular plates have been solved in [12-14].Since the basic equations of moderately thick ORP are more complex than these of moderately thick isotropic rectangular plate,it becomes more difficult to solve the specific boundary condition problems analytically.As far as we know,moderately thick ORP with four sides free on Winkler foundation has not been studied by any analytical methods so far.Therefore,based on the boundary conditions and basic equations of the bending of moderately thick ORP on Winkler foundation,the analytical bending solution of this plate is studied by using the FIT method and its corresponding inverse transform method.Finally,a number of deflection values of isotropic and orthotropic rectangular plates with different thicknesses are calculated by using the obtained analytical solution and some of the calculated results are compared with those in [12,15].And the comparison results show that the obtained FIT solution is correct.

2.Basic Equations and the Boundary Conditions

The basic equations of moderately thick ORP on Winkler foundation[16]are

The bending momentsMxandMy,the twisting momentMxyand the shear forcesQxandQycan be expressed as

The boundary conditions of moderately thick ORP with four sides free can be expressed as

3.Solving Basic Equations by FIT

By the double FIT,W(x,y),ψx(x,y) andψy(x,y) can be expressed as

The integral transforms shown in Eqs.(3.1)-(3.3)are applied to the basic equations(2.1),and we obtain

The double FIT of the loadq(x,y) is

Then Eqs.(3.10)-(3.12) can be written as:

The coefficientsPij(i=1,2,3;j=1,2,···,5) are given in Appendix A.

Substituting Eqs.(3.18)-(3.19) into Eqs.(3.5)-(3.6),and combining the boundary conditionsMx|x=0,a=My|y=0,b=0 and the Stokes transformation[17],we obtain

Eqs.(3.20)-(3.23) are four infinite equations about the undetermined constantsKn,Ln,ImandJm(n,m=0,1,2,···).Use Mathematica software to calculateKn,Ln,ImandJm,and then substitute them into Eq.(3.17) to get ˜W(m,n).By substituting the obtained ˜W(m,n)into Eq.(3.4),the analytical bending solution of moderately thick ORP with four sides free on Winkler foundation can be obtained.It is worth noting that there are infinite numbers of undetermined constantsKn,Ln,ImandJm(n,m=0,1,2,···).However,when solving practical problems,we can obtain series expansion solutions with required accuracy by taking sufficiently largenandm.

4.Examples

Here we apply the FIT solution obtained in this paper to calculate the deflection values of isotropic and orthotropic square plates with different thicknesses on Winkler foundation.In order to achieve sufficient calculation accuracy,we takenandmto 1500 in the following two examples.

Example 4.1Here we calculate some deflection values of the four sides free thin,moderately thick and thick isotropic square plates on Winkler foundation subjected to a concentrated loadPat the center of the plates.The corresponding parameters are taken asK=100D/a4,D11=D22=D,D12=νD,D66=(1-ν)D/2,C11=C22=Candν=0.3.The calculated results are compared with those in [15],as shown in Tab.4.1(the numerical results retain five significant digits).

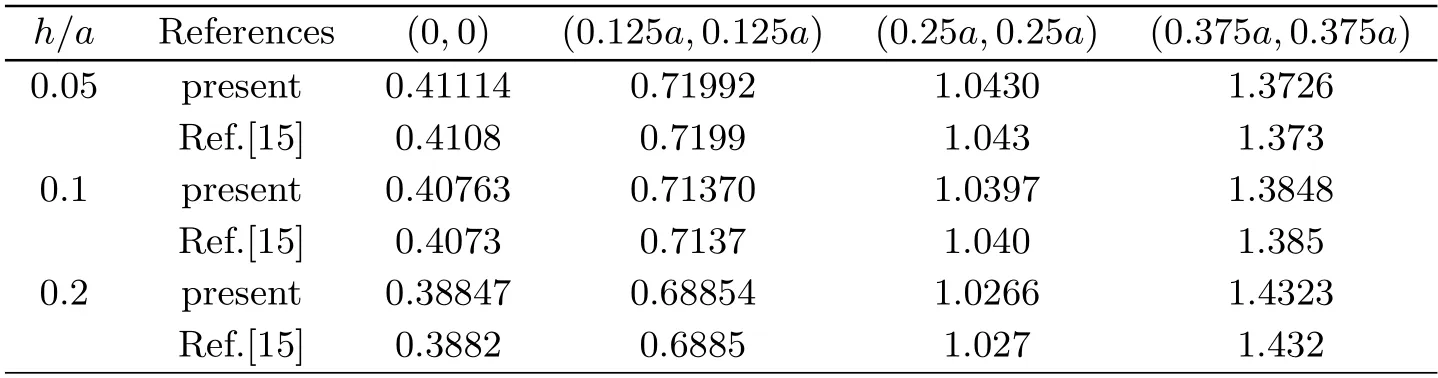
Tab.4.1 Deflections W (Pa2/100D)of isotropic square plates with four free edges

Example 4.2Here we calculate some deflection values of the four sides free thin,moderately thick and thick orthotropic square plates on Winkler foundation subjected to a concentrated loadPat the center of the plates.When calculating thin plates,we take the corresponding parameters asK=100D11/a4,ν1=0.1,ν2=0.4,D12=0.4D11,D22=4D11,D66=0.3D11,C11=12D11/h2,C22=48D11/h2andk=5/6 ;When calculating moderately thick plates(h/a=0.1)and thick plates(h/a=0.2),the corresponding parameters are taken asK=100D11/a4,E1/E2=10,ν1=0.25,G12=0.5E2andk=5/6.The numerical results obtained from the calculation of the thin plate are compared with the results in[12],as shown in Tab.4.2(the numerical results retain five significant digits).

Tab.4.2 Deflections of orthotropic square plates with four free edges

RemarkFrom the calculation process of the FIT solution,we can know that the FIT solution obtained in this paper can calculate not only the concentrated load,but also the uniform load,linear load,continuous load and local load and other common loads.

5.Conclusion

The analytical bending solution of moderately thick ORP with four sides free on Winkler foundation is derived by the FIT method.Compared with the classical inverse or semi-inverse method,the FIT method is not required to select any pre-determined trail function,and the solution process has good generality.It can be seen from specific examples that the FIT solution obtained in this paper can uniformly calculate isotropic and orthotropic rectangular plates with different thicknesses.Furthermore,this FIT method can also be put to use in studying the bending,vibration and buckling of isotropic and orthotropic rectangular plates with different thicknesses under more boundary conditions and different types of loads.

Appendix A

The elementsPij(i=1,2,3;j=1,2,3,4,5) in Eqs.(3.17)-(3.19) are: