具有两阶段故障的流模型近似解分析

刘煜飞,叶晴晴

(南京信息工程大学数学与统计学院,江苏 南京 210044)

1.引言

流模型研究了一类输入输出系统,此类系统在许多领域具有广泛的应用,例如制造系统[1]、计算机通信系统[2]、视频流量[3]等领域,作为具有离散单元的标准排队系统的近似,流模型可为系统优化提供参考.关于流模型的具体介绍和经典参考文献的综述,可参阅文[4].

完全可靠的排队系统在现实生产生活中几乎不存在,因此,具有故障或工作故障策略的排队系统在过去几十年里受到了相当多的关注,对于具有故障策略的排队系统研究可以追溯到文[5],对于具有部分故障策略的排队系统研究可以追溯到Kalidass等文[6]及其参考文献.随后,众多学者考虑了具有各种特征的不可靠排队系统.Sherman等[7]研究了具有无限容量的不可靠M/M/1重试排队系统,并给出了该系统的平稳条件与系统性能指标的显示解.YE等[8]研究了具有工作故障的MAP/M/1排队系统,利用矩阵几何解法得出了系统在稳态下的客户数,并对系统性能指标进行了分析.GAO等[9]研究了具有灾难与故障策略的离散时间排队系统,利用嵌入式马尔可夫链和补充变量法,确定了顾客到达前时刻与任意时刻的系统队长分布,并得到了顾客在系统中的逗留时间.YANG等[10]研究了一个具有异构服务器的M/M/2排队系统,利用拟生灭过程与矩阵几何解法得到了系统的平稳分布,并利用粒子群优化算法对系统的近似最优服务率进行数值求解.

很少有学者研究具有故障或工作故障策略的流模型.Vijayalakshmi和Thangaraj[11]研究了由生灭过程驱动的流模型,利用Laplace变换与连分数,得到了该模型性能指标的稳态概率分布.Vijayashree等[12]研究了一个由具有灾难与后续修复的M/M/1/N排队系统驱动的流模型,该驱动系统在进行维修时将以较低的速率为到达系统的流体提供服务,通过构建该模型所满足的微分差分方程组,利用第一类Bessel 函数得到了该流模型库存量稳态概率分布的显式表达式.Vijayashree等[13]在文[12]的基础上将驱动系统拓展为具有灾难与后续修复的M/M/1排队系统,利用该模型所满足的微分差分方程组与Laplcae变换,得到了该排队系统库存量的稳态概率的精确表达式.Seenivasan等[14]研究了一个包含工作休假和故障的多服务器流模型,利用矩阵几何解法得到了该流模型库存量的稳态分布.Felicia等[15]研究了带有反馈顾客和故障的M/M/1排队系统驱动的流模型,并通过Laplace变换得到了库存量的平稳分布.Nabli[16]在研究有限状态不可约马尔可夫链驱动的流模型中,提出了一种基于递推关系的用于逼近流模型库存量尾分布的算法,并给出了计算截断步长(Truncation step)的算法.

随着现代计算机技术的发展,社会中对于大数据产品业务的需求不断增长,为了提供此类产品,供应商增加了服务器的数量,与此同时维护此类服务器的压力也随之增大.各种软、硬件故障而造成的业务中断成为影响大数据服务稳定性的重要因素之一.为了减少因故障而产生的服务中断,大数据服务供应商不约而同的开始了硬件自愈的研究.在阿里云对于硬件自愈[17]的研究中提及当系统发现故障发生时,系统将启动一阶段维修,在降低服务速率的同时开始维修,当维修完成时再以正常服务速率提供服务;若在一阶段维修时再次出现故障,系统将停止服务进行彻底的维修.本文受这类硬件自愈研究与流模型的启发,考虑了一个具有两阶段故障策略的流模型,即当系统处于正规忙期时若故障发生,系统将进入部分故障期并立刻开始维修,且在维修期间缓冲器将以较低的服务速率为到达系统的流体提供服务,直到维修完成系统重新进入正规忙期;若当系统处于部分故障期时再次发生故障,系统将完全停止服务并继续维修,直到维修完成后进入正规忙期.不失一般性,本文使用流体到达速率作为流模型的输入率,使用缓冲器的输出速率作为流模型的输出率.

本文将两阶段故障策略与流模型相结合,利用归一化技术,通过递推得到了该流模型库存量尾分布函数的近似解,并给出了给定误差限下截断步长的计算方式,为该模型性能指标的求解提供了一种新的方法.其理论成果存在潜在的应用,可将该模型应用于云计算服务中具有硬件自愈的系统分析中.

2.流模型描述

考虑具有两阶段故障的流模型,假设如下: 流体以参数为λ的泊松流到达缓冲器,即流体的输入速率为λ.当系统处于正规忙期时,流体的输出速率为µ.在正规忙期内,每次故障发生的间隔时间服从参数为α的指数分布,即故障的发生服从参数为α的泊松过程,一旦遭遇故障,系统将进入部分故障期,其长度服从参数为β的指数分布.在部分故障期内,流体的输出速率降低为η(η<µ).在部分故障期内,缓冲器可能再次遭遇故障,不失一般性,假设在部分故障期内故障的发生也服从参数为α的泊松过程.一旦处于部分故障期内的缓冲器遭遇故障,系统将进入完全故障期,其长度服从参数为β的指数分布.当完全故障期结束时,系统将进入正规忙期.假设顾客到达的时间间隔,缓冲器在正规忙期的输出速率,缓冲器在部分故障期的输出速率,故障发生时间与维修时间相互独立.此外,假设服务顺序为先进先出(FIFO).

该流模型的状态可以用马尔可夫过程X=(X(t),t ≥0)来表示,其中:X(t)为时刻t流模型所处的状态,且

状态空间为S=(0,1,2),对应的无穷小生成元为

令Q(t)表示时刻t的库存量,且为非负随机变量.设流模型库存量的净输入速率(输入速率-输出速率)为二维随机程{(Q(t),X(t)),t ≥0}的函数,满足

其中,d0>0,d2<0,d1符号待定.具体来说,当流模型处于完全故障期时,库存量将以速率|d0|线性增加;当流模型处于正规忙期时,库存量将以速率|d2|线性减少;当流模型处于部分故障期时,库存量将以速率|d1|线性变化(d1>0时增加,d1<0时减小,d1=0时不变).当库存量为空时,流模型所处的状态不会发生改变,且只有故障发生或修复完成时流模型的状态才会改变.此外,定义依赖于净输入速率的状态空间

定义π=(π0,π1,π2)为X=(X(t))的稳态概率.行向量π满足

其中,0与1分别是由0和1构成的三维行向量,T为转置算子.该流模型的稳态条件为

因此,过程{(Q(t),X(t)),t ≥0}是一个二维马尔可夫过程,定义该马尔可夫过程在时刻t的尾分布函数为

当稳态条件(2.5)成立时,记过程{(Q(t),X(t)),t ≥0}的极限分布为{Q∞,X∞}.令

为了便于表示,引入矩阵

由文[18],行向量F(x)满足下列微分方程

其中,F′(x)为F(x)在x处的导数.为了求解尾分布函数Fi(x),需要求解微分方程(2.10),并确定初始条件F(0).当Fi(x)确定时,流模型库存量在稳态条件下的尾分布函数可由全概率公式计算得到

同时,该流模型的平衡方程(输出速率=输入速率)可表示为

3.模型分析

在本部分中,本文将使用归一化技术求解具有两阶段故障的流模型尾分布函数的近似解,并给出计算截断步长的算法,详细的理论可参阅文[16].令a=max(-aii),其中:aii为矩阵A的第i个对角线元素,事实上a=α+β.同时,令d=min{di|di>0}.随后定义

其中:I是一个三维单位矩阵.显然,矩阵P是随机的,即矩阵P的所有元素都是非负的且每一行和为1.此外,矩阵P满足

由式(2.2)与稳态条件(2.5),可以确定d0>0且d2<0,但d1的符号是不确定的,故本部分将根据d1的符号进行分类讨论,用递推表达式给出库存量Q(t)的尾分布函数的近似解.

情形一d1>0

由于d1>0且d0>0,d2<0,故矩阵D是可逆的,由式(2.10),可得

随后,需要确定初始条件F(0).由式(2.3),d1>0时依赖于净输入速率的状态空间为S+={0,1}与S-={2}.显然,当X(t)=0,1时,库存量Q(t)以概率1满足Q(t)>0,故当i=0,1时,Fi(0)=πi.此外,由平衡方程(2.12)与S-={2},得F2(0)=-(d0π0+d1π1)/d2.在下面的定理中,将给出一个数值稳定的算法来计算向量F(x).

定理3.1当稳态条件(2.5)成立时,对于任意实数x ≥0,尾分布函数Fi(x)满足

其中系数bi(k)≥0且满足: 当k=0时,

证矩阵AD-1可以写成分块矩阵的形式

注意到,d/d2<0而1-αd/ad2>1,在进行计算时可能会发生正负抵消而使得算法不稳定.为了避免这一问题,给出另一个与i=2有关的递推式,在这个式子中将只出现正数.

定义行向量d=(d0,d1,d2),可得

对于所有整数k,可得

考虑到b(0)=F(0),可得

由此,得到d0b0(k)+d1b1(k)+d2b2(k)=0,这就是定理中提到的与i=2相关的表达式.

由参数d与α的定义,可知α/a,β/a与d/di,i=0,1都是以1为界的正数,此外1-dβ/d0α与1-d/d1是非负的.由于bi(0)=Fi(0)且Fi(0),i=0,1,2是非负的,使用归纳法可证明对于所有k ≥0,有

证毕.

由式(2.11),可得

下一个定理将证明数列(bi(k))k∈N的单调性和收敛性.

定理3.2当i=0,1,2时,(bi(k))k∈N是一个以πi为上界的递减数列,且满足

证首先,通过归纳法证明数列(bi(k))k∈N的单调性.当i=1时,

由于b(0)=F(0),可得

考虑到πP=π,即π1[1-(α+β)/a]+π2α/a=π1,得到

由π0(1-β/a)+π2α/a=π0,得到

后,对b0(2)与b0(1)作差,得到

由于b0(1)-b0(0)=0,b1(1)≤b1(0),得到

由b2(0)=F2(0)=π2-P {Q=0}且d/d2<0,得到

由参数的定义,可知d/d0∈(0,1],d/d1∈(0,1],d2<0,同时α/a ∈(0,1],β/a ∈(0,1],(α+β)/a=1.由此,可以通过归纳法证明当i=0,1,2时,数列(bi(k))k∈N是单调递减的.其次,证明数列(bi(k))k∈N的收敛性.由于数列(bi(k))k∈N是非负且递减的,其极限一定存在.令li为数列(bi(k))k∈N的极限.由式(3.4),当x趋向无穷时,可得

由于当x趋向无穷时,尾分布函数Fi(x)=P {Q(t)>x,X(t)=i}趋向于0,故极限li必须为0.证毕.

为了计算定理3.1中给出的无穷级数,下面给出了一个算法,该算法可以保证结果误差不超过给定的误差限ε.对于一个给定的正实数x,首先定义泊松级数的截断步长为R(x),满足

具体的计算方式,可参阅文[19].由于数列(bi(k))k∈N的单调性与收敛性,定义另一个截断步长

由定理3.1和式(2.11),可得

同时,误差项e(n0)满足

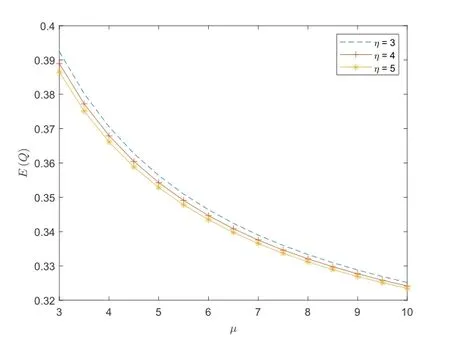
且,当R(ax/d)

当R(ax/d)≥nε时,由k>nε时b(k)1T≤ε,得

从数值计算的角度来看,若想要计算库存量的尾分布,并使得计算误差在给定的误差限ε内,只需要对式(3.4)从0到n0求和即可.

情形二d1≤0

由于d1≤0,无法确定矩阵D是否可逆.此时,有S+={0}且S-={1,2}.求解式(2.10)在初始条件下的解这一问题可以转化为下列有解问题

引理3.1[17]当i=0,1,2,n ∈N+且k=0,···,n-1时,可得

引理3.2[17]当n ∈N+且k=0,···,n-1时,可得

定理3.3式(3.31)存在一个解为Gi(x),且Gi(x)满足

证与文[17]中定理3.4的证明类似.

由初始条件b0(n,0)=π0,b1(n,n)=b2(n,n)=0与式(3.2),可得d/d0=1,d/(d-di)∈[0,1],i=1,2,故当i=0,1,2时,数列bi(n,k)满足

由于数列(bi(n,k))n≥k是以πi为上界的单调递减数列,由引理3.1,其极限bi(k)存在.

为证明当稳态条件(2.5)成立时行向量G(x)=(G0(x),G1(x),G2(x))是式(3.31)的一个解.根据定理3.3中给出的递推式,可得

定理3.4当稳态条件(2.5)成立时,式(3.31)存在唯一解.

证与文[17]中定理3.5的证明类似,证明将分为2部分,即d1<0与d1=0.

当d1<0时,矩阵D是可逆的,此时式(2.10)可改写为

与定理3.1类似,当向量F(0)确定时,库存量尾联合分布函数F(x)便可以唯一确定.由稳态条件(2.5)可知F(0)是唯一的.同时注意到当i=0,1,2时Fi(x)=0,且F0(0)=π0.由文[17]中定理3.4,此时式(3.31)的解是唯一的.

当d1=0时,定义状态空间S0={1}与={0,2}.矩阵A与对角矩阵D可以改写为以下形式

利用文[17]中定理3.5的证明方式,即可证明此时式(3.31)的解是唯一的.综上,当d1≤0时式(3.31)的解是唯一的.证毕.

由定理3.3与定理3.4,流模型库存量的尾联合分布函数可以表示为

从数值计算的角度来看，当(b(n,k))0≤k≤n=(b0(n,k),b1(n,k),b2(n,k))0≤k≤n确定后，便可得到库存量尾联合分布函数F(x).

为了计算定理3.3中给出的无穷级数,与d1>0的情况类似,下面给出一个算法,该算法可以保证库存量尾分布函数误差不超过给定的误差限ε的2倍.在计算库存量尾分布前需要确定系数bi(k),即(n,k).故,首先定义截断步长n∞为bi(n,k)的迭代次数.由推论3.1,可以寻找到一个n∞使得b(n∞,n∞)1T≤ε.同时,注意到,存在一个n∞,满足

故,截断步长n∞最终可定义为

由数列(bi(n,k))0≤k≤n的定义,可得

故,对于k=0,1,···,n∞-1有

由此,对于任意的k ∈N,数列b(n,k)1T

n的极限将在n∞取得,即对于任意的k ∈N

为了提高计算库存量尾分布函数的效率,定义另一个截断步长n0,满足

由于n∞的存在,保证了b(n∞,n∞)1T≤ε,故截断步长n0一定小于n∞.由式(3.33)与式(2.11),流模型库存量尾分布的近似解可由下列表达式给出

通过对部分工作状态下流模型净输入率d1的分类讨论,本文最终得到了库存量的尾分布函数的近似解,并通过确定截断步长,使得该近似解的误差不超过给定误差限ε的2倍.

4.库存量的矩

5.数值例子

假设顾客流以参数为λ的泊松流到达某云计算服务系统缓冲器.该云计算服务系统允许发生两次故障,且故障发生的间隔时间服从参数为α的指数分布,修理时间服从参数为β的指数分布.在正规忙期内缓冲器的输出速率为µ,故障发生时,系统将进入部分故障期,输出速率降低为η(η<µ).系统处于部分故障期时,若再次发生故障,系统将完全停止工作,直到修复完成后,系统进入正规忙期.基于以上假设,本部分将云计算服务中顾客到达视为输入系统的流体,将服务器视为流模型中输出流体的缓冲器,构建了一个具有双阶段故障的云计算服务流模型.

情形一d1>0

当d1>0时,顾客流体的到达速率λ大于流模型在部分故障期内缓冲器输出速率η.

当λ=2.5,α=1,β=1.25时,图5.1给出了部分故障期内缓冲器输出速率η分别为1.6,1.8,2.0的情况下平均库存量E(Q)随正规忙期内缓冲器输出速率µ的变化趋势图.可以看出,随着参数µ的增大,平均库存量E(Q)不断减小,并趋于一个接近于0的常数.

当α=1,β=1.25,η=2时,图5.2给出了正规忙期内缓冲器输出速率µ分别为10,11,12的情况下平均库存量E(Q)随顾客流体到达速率λ的变化趋势图.可以发现,随着到达率λ的增加,平均库存量也会增加.在到达率λ相同的情况下,正规忙期内缓冲器输出速率µ越大,平均库存量越小.

图5.2 d1 >0时E(Q)随µ和λ的变化曲线

当α=1,β=1.25,λ=5,µ=15时,图5.3给出了部分故障期内缓冲器输出速率η分别为4.0,4.2,4.4的情况下库存量尾分布函数P {Q∞>x}的变化趋势图.显然,当x增大时,尾分布函数P {Q∞>x}趋向于0.同时,部分故障期内缓冲器输出速率η越大,尾分布函数P {Q∞>x}将越快的趋向于0.

当α=1,β=1.25,λ=2.5,µ=4.4,η=1时,表5.1中展示了对于给定误差限ε=1×10-9与不同x的取值下获得的截断步长nε与R(ax/d).不难发现,当系统参数固定时,截断步长R(ax/d)随着x的增加而增加,但是截断步长nε是固定的.因此,当x较小时,可以选择R(ax/d)作为计算尾分布函数截断步长,但随着的x的增大,应该选择nε作为截断步长.

表5.1 不同x取值下的截断步长

情形二d1=0

当d1=0时,顾客流体到达速率λ与流模型在部分故障期内缓冲器输出速率η相同.

当α=1,β=1.25时,图5.4给出了顾客流体到达率λ与部分故障期内缓冲器输出速率η相同时平均库存量E(Q)随到正规忙期内缓冲器输出速率µ的变化趋势图.可以发现,随着输出速率µ的增加,平均库存量随之减小.且与d1>0情况下的图5.1相比,平均库存量E(Q)的值有显著的下降.

图5.4 d1=0时E(Q)随µ的变化曲线

当α=1,β=1.25,µ=15时,图5.5给出了库存量尾分布函数P {Q∞>x}的变化趋势图.与图5.3进行对比,可以发现,P {Q∞>x}在x=0处的值明显更小,这说明流模型库存量Q(t)有更大的概率处于Q(t)=0,即系统库存量将更容易清空.

图5.5 d1=0时P {Q∞>x}随x的变化曲线

情形三d1<0

当d1<0时,顾客流体到达速率λ小于流模型在部分故障期内缓冲器输出速率η.

当α=1,β=1.25,λ=2.5时,图5.6给出了部分故障期内缓冲器输出速率η分别为3,4,5的情况下平均库存量E(Q)随正规忙期内缓冲器输出速率µ的变化趋势图.可以发现,随着输出速率µ的增加,平均库存量随之减小.且与图5.1,图5.4相比,平均库存量E(Q)的值更小.

图5.6 d1 <0时E(Q)随µ和η的变化曲线

表5.2给出了当α=1,β=1.25,λ=2.5,µ=15时库存量尾分布函数P {Q∞>x}的变化趋势.仍然可以发现,随着x的增大,P {Q∞>x}的值随之减小.同时,在相同的x取值下,η越大,P {Q∞>x}的值越小.

表5.2 d1 <0时P {Q∞>x}随η与x的变化

由图5.1-5.6与表5.1-5.2可知,在存在硬件故障的云计算服务系统中,若想减少系统中顾客的排队现象,降低顾客的平均等待时间,有以下解决方案: 1)提高正规忙期、部分故障期内的服务速率;2) 降低服务器发生故障的频率,提高服务器无故障工作时间;3) 提高维修效率,降低服务器维修所需要的时间.

6.总结与展望

本文研究了具有两阶段故障的流模型,利用归一化技术,得到了具有两阶段故障的流模型库存量尾分布函数的递推表达式,同时给出了给定误差限条件下截断步长的计算方式,并给出了流模型各阶矩的表达式.最后将该流模型应用于云计算服务中,利用数值例子分析系统参数对整体系统性能指标的影响.

本文只研究了允许发生两次故障的流模型,然而考虑到只允许发生两次故障的系统在现实生产生活中占比较少,在未来的研究中可以考虑具有更多工作状态的流模型.也可将N-策略、负顾客等其他策略加入流模型中,并考虑如何优化系统才能给社会带来更多的经济效益.另一方面,在故障流模型中加入带宽共享网络中用户的延迟因素是未来可行的研究方向.最后,还可以在包级模型和流级模型间严格连接方面进行研究.