相协样本下概率密度函数的调整经验似然推断

王宁宁,秦永松

(广西师范大学数学与统计学院,广西 桂林 541006)

1.引言

经验似然是Owen[1-2]在独立样本下提出的一种非参数统计推断方法,与经典方法(如正态逼近理论)以及当前比较流行的统计方法(如Bootstrap)相比,经验似然方法具有诸如: 置信域的形状由数据决定、置信域具有Bartlett可修正性、无需构造枢轴量、具有保值域性和函数变换不变性等优点.正因为如此,许多统计学家将这一方法应用到各种统计模型及各种领域.如线性回归模型的统计推断[3-4],分位数统计推断[5]、广义线性统计推断[6]等,此外CHEN[7]将经验似然方法与核方法结合构造精度更高的概率密度函数的置信区间等.然而,上述文献所提到的经验似然方法都针对于独立样本情形,而现实中相协样本情形经常出现,针对于相协样本,现有的研究较多采用分块经验似然方法进行推导.Kitamural[8]在α-混合样本下首次运用分块经验似然方法构建参数的置信区间.此后,ZHANG[9]将分块经验似然用于构造负相协样本下非参数整体均值的置信区间、LEI和QIN[10]将分块经验似然用于构造负相协样本下总体分位数的置信区间、QIN等[11]将分块经验似然用于构造负相协样本下概率密度函数的置信区间等.

为了保证经验似然统计量的存在,需要假定0在数据的凸包内,针对0向量可能不在数据的凸包内的问题,CHEN等[12]提出了调整经验似然.此后CHEN和HUANG[13]使用调整经验似然构造总体均值的置信区间并研究了其有限样本下的性质,ZHOU和JING[14]使用调整经验似然构造分位数的置信区间等.本文受到文[12,15]的启发,研究相协样本[16]下概率密度函数的调整经验似然推断问题,采用不分块的调整经验似然方法进行推导避免了分块技术的复杂性,并构造了相协样本下概率密度函数的调整经验似然置信区间.通过模拟得到,调整经验似然(AEL)的表现略优于经验似然(EL) 和正态逼近(NA).

本文结构如下: 第2节将给出本文的主要结论,第3节将给出有限样本下的模拟结果,第4节将给出相关的引理及其证明,第5节将给出主要结论的证明.

2.主要结论

设X1,X2,···,Xn是来自总体X的一组严平稳相协样本,f(x)为X的概率密度函数,给定x ∈R,f(x)的核密度估计为

通过拉格朗日乘数法可以得到pi=1/[(n+1)(1+λgn,i(θ))],其中λ=λ(θ)满足

则对数调整经验似然比统计量为

下面我们列出一些正则条件,这些正则条件将会用在后面的定理中.通常设C为正常数,在不同情况下可能取到不同的数值.

正则条件:(A1)(i)X1,···,Xn为严平稳相协序列(正相协或者负相协);

(A3) 设pn,qn为正整数且满足:pn+qn ≤n,kn=[n/(pn+qn)],其中[t]表示t的整数部分.设hn>0为窗宽,且pn,qn和hn分别满足

注2.1本文中条件(A1)-(A3)与文[16]中条件(A1)-(A3)完全相同.条件(A1)(v),(A2)(iii),(A3)(iv)与文[16]推论2.1中条件(b)相同.若f在x的邻域内有连续的一阶导函数,可用文[16]中的条件(a)代替(A1)(v),(A2)(iii),(A3)(iv).

本文主要结论为以下内容.

定理2.1设条件(A1)-(A3)成立且an=o(n),则当n →∞时有

注2.4定理2.1用于构造f(x)的调整经验似然置信区间.令Zα满足P(≥Zα)=α,其中0<α<1,则f(x)基于(1-α)的调整经验似然的置信区间为

为了进一步研究当θf(x)时,对数调整经验似然比统计量W∗(θ)和对数经验似然比统计量W(θ)的功效,我们引入定理2.2.

定理2.2假设定理2.1的条件(A1)-(A3)成立且an=o(n2/3),对于θf(x),当n →∞时,依概率趋于1有-2(nh)-1/3W∗(θ)→∞且-2(nh)-1/3W(θ)→∞成立.

注2.5定理2.2表明,当θf(x)时,对数调整经验似然比统计量W∗(θ)和对数经验似然比统计量W(θ)以至少(nh)1/3的速率趋于无穷大.

3.模拟结果

本节通过模拟来研究式(2.2)所示的AEL置信区间在有限样本下的表现.用AELCI表示式(2.2)所示的AEL置信区间,ELCI表示文[15]中式(2.7)所示的EL置信区间,NACI表示式(3.1)中所示的NA置信区间,即

Ⅰ 负相协样本

i) 多元正态分布随机样本

在本节模拟中,(X1,···,Xn)是多元正态随机向量,且满足E(X1,···,Xn)=(1,···,1),Cov(Xi,Xj)=-4-(j-i)-1(1≤i ≤n,j>i)和V ar(Xi)=0.52(1≤i ≤n),取an=1,由此生成的{Xi;1≤i ≤n}是负相协序列(见文[17]),该情形下的模拟结果见表1.

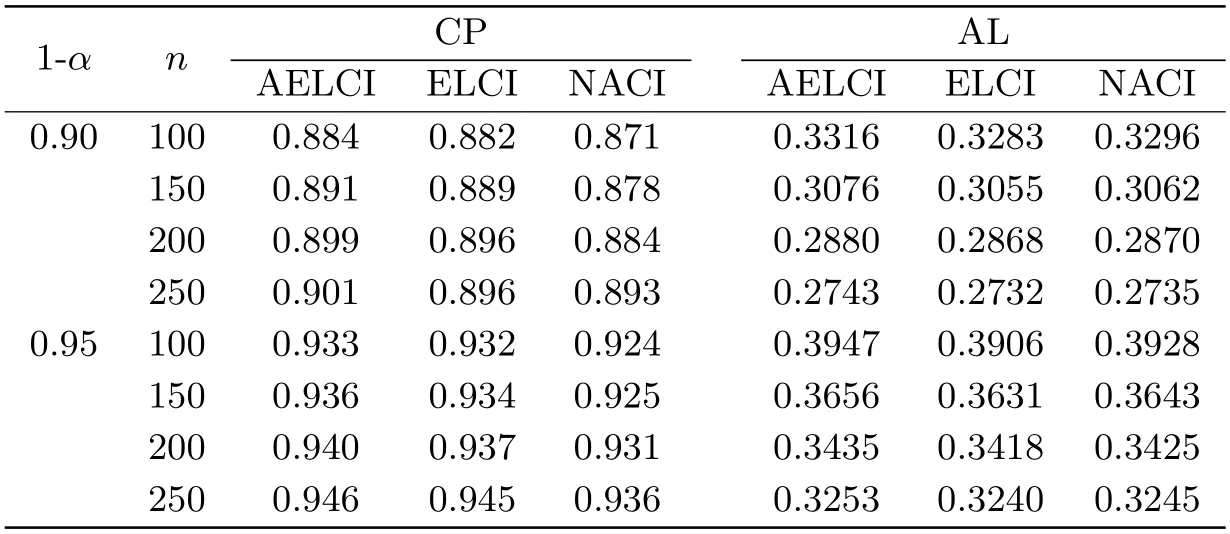
表1 多元正态分布随机样本下置信度为0.90和0.95时f(1)的置信区间的CP和AL

由表1得,在多元正态随机样本下,随着样本量的不断增大,置信区间的覆盖率逐渐增大且越来越接近于置信度,置信区间的平均长度逐渐减小.当n相同时,AEL方法的置信区间的覆盖率高于EL和NA两种方法的置信区间的覆盖率,虽然AEL方法置信区间的平均长度略大于EL和NA两种方法的置信区间的平均长度,但是相差非常小.因此综合分析可得,多元正态随机样本下,AEL的表现略优于EL和NA的表现.

ii) 多元t分布随机样本

在本节模拟中,(X1,···,Xn)是多元t分布随机向量,且满足E(X1,···,Xn)=(1,···,1),Cov(Xi,Xj)=-3-(j-i)-1(1≤i ≤n,j>i) 和Var(Xi)=5/3(1≤i ≤n),取an=0.5,由此生成的{Xi;1≤i ≤n}是负相协序列(见文[17]),该情形下的模拟结果见表2.

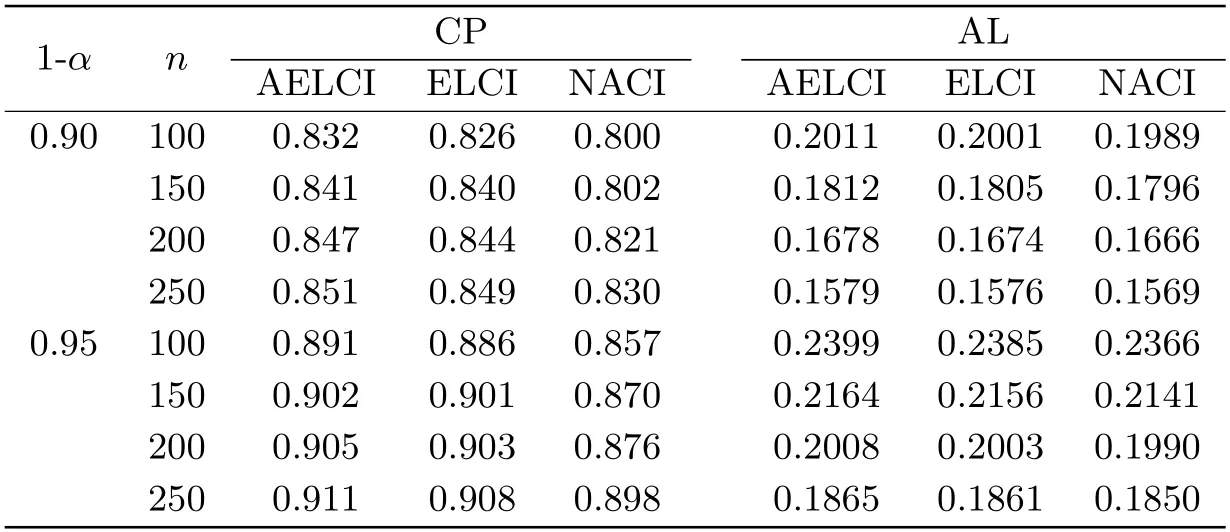
表2 多元t分布随机样本下置信度为0.90和0.95时f(1)的置信区间的CP和AL

由表2得,在多元t分布随机样本下,随着样本量的不断增大,三种方法的置信区间的覆盖率均逐渐增大且越来越接近置信度,置信区间的平均长度均不断减小.当n相同时,AEL方法的置信区间的覆盖率高于EL和NA两种方法的置信区间的覆盖率,尽管其置信区间的平均长度也稍有增加,但与EL和NA的置信区间的平均长度相比相差甚微.综合分析可得在多元t分布随机样本下,AEL表现略好于EL和NA的表现.

因此一般来说,在正相协随机样本下,AEL表现略好于EL和NA的表现.此外,通过对比两种不同分布随机样本下的模拟结果可得,当n取同一值时,多元正态分布样本下三种方法的置信区间的覆盖率都更高且更接近于置信度,因此可得三种方法在多元正态分布随机样本下的表现均优于在多元t分布随机样本下的表现.

Ⅱ 正相协样本

由表3、表4得,从置信区间覆盖率来看,随着样本量的不断增大,两种随机分布样本下置信区间的覆盖率均不断增加且越来越接近置信度,当n相同时,AEL的置信区间的覆盖率高于EL和NA的置信区间的覆盖率.从置信区间的平均长度来看,两种随机分布样本下置信区间的平均长度均随着样本量的增加不断减小.尽管AEL方法在置信区间的覆盖率增大的同时其平均长度也稍有增加,但其与EL和NA的置信区间的平均长度相比相差甚微.

表3 ∼N(1,1)情形下置信度为0.90和0.95时f(1)的置信区间的CP和AL

表3 ∼N(1,1)情形下置信度为0.90和0.95时f(1)的置信区间的CP和AL

表4 ∼情形下置信度为0.90和0.95时f(1)的置信区间的CP和AL

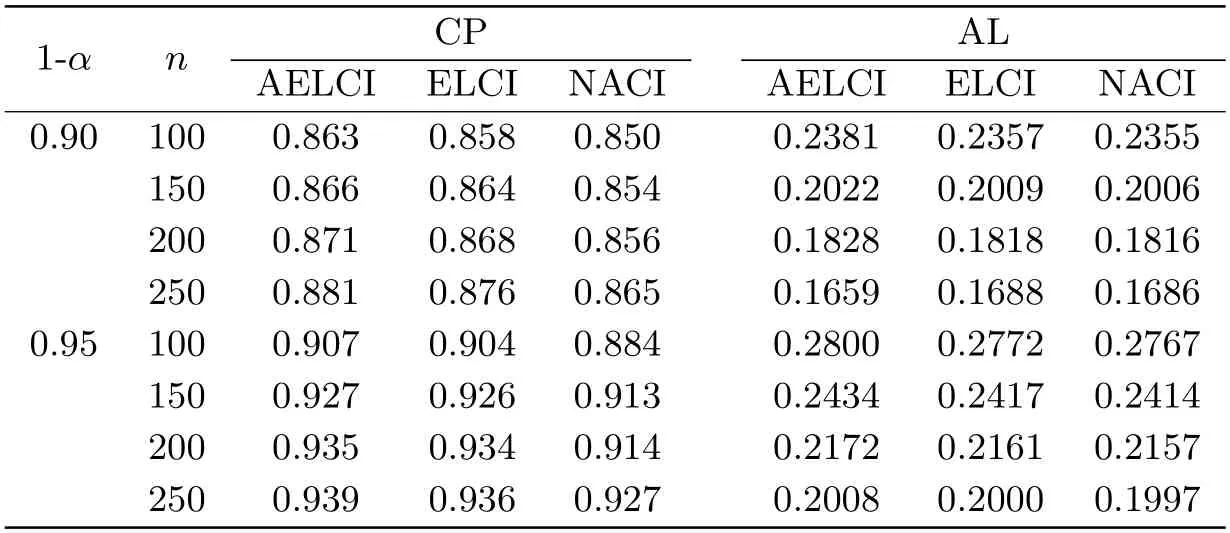
表4 ∼情形下置信度为0.90和0.95时f(1)的置信区间的CP和AL

综合分析可得,正相协样本下,AEL的表现略好于EL和NA.此外,通过两表对比可得,当n取相同值时,正态分布样本下三种方法对的置信区间的覆盖率更高且更接近于置信度,且置信区间的平均长度也更短,由此可得三种方法在正态分布随机样本下的表现优于在卡方分布随机样本下的表现.

综上可得,相协样本下(正相协或负相协),对于概率密度函数置信区间的估计,AEL方法的表现略好于EL和NA两种方法的表现,且三种方法均在正态分布随机样本下表现得更好.

此外,通过模拟结果发现,在相协样本下文中提到的三种方法得到的置信区间的覆盖率一致低于名义覆盖水平1-α,尝试增大样本量进行模拟发现(模拟结果不再列出),置信区间的覆盖率有所改善且偶尔出现高于置信度1-α的情形,但是与样本量较小时模拟结果相比,样本量增大时AEL方法的表现优于EL和NA的表现的程度有所下降.因此,AEL方法更适合在样本量较小时使用,在样本容量较大时,EL和AEL的表现相差不大.在独立样本情形下,Tsao[18]讨论了EL置信区间的覆盖率常常低于名义覆盖水平的情况,并且从理论上分析了出现这一现象的原因,相协样本情况下EL置信区间出现低覆盖的原因尚需进一步研究.

4.引理

以下引理将用于后面定理的证明,其中引理4.1-4.3的证明见文[15]的引理4.1-4.3的证明.

引理4.11)设条件(A1)(i)-(iv),(A2)(i)(ii),(A3)(i)-(iii)成立,则对于f的连续点x有

2)设条件(A1)-(A3)成立,则

引理4.2设条件(A1)(i)(v)和(A2)(i)成立.则对于任意的l ∈n有

引理4.3设条件(A1)-(A3)成立,则

引理4.4设条件(A1)-(A3)成立,则

5.定理证明

定理2.1的证明1) 首先证明

利用最大化问题的对偶性可得

因为M可任意大,则对于θf(x),当n →∞时,依概率趋于1有-2(nh)-1/3W∗(θ)→∞成立.对于-2(nh)-1/3W(θ)→∞的证明与-2(nh)-1/3W∗(θ)→∞的证明相似.

定理2.2证毕.