基于扰动观测器的PMSM系统自适应反步滑模控制*

黄 刚,万雨龙

(湖南工业大学轨道交通学院,株洲 412007)

0 引言

永磁同步电机(permanent magnet synchronous motor,PMSM)由于其结构简单、功率密度高、性能高和损耗低,被广泛应用于机器人、运输、电梯和机床等工业领域中[1]。作为一个非线性系统,永磁同步电机控制系统在各种条件下运行时,往往会因非线性、参数不确定性和外部扰动而失真,从而导致系统出现不理想的动态响应[2]。在这种情况下,使用传统的线性反馈控制可能无法保证电机系统的整体性能。因此,需要一种替代方法来保持电动机驱动器的高动态性能。目前已有多种非线性控制方法来提高电机系统的控制性能,包括反步控制[3]、自适应控制[4]、模糊逻辑控制[5]、滑模控制[6]和模型预测控制[7]等。在这些方法中,反步控制是一种基于Lyapunov稳定性理论的非线性系统的系统迭代和递归方法,它确保了全局渐近稳定性[8]。这种方法可以将复杂的非线性控制系统转化为简单的降阶子系统[9]。通过递归设计和虚拟控制变量,可以导出用于电机位置跟踪或速度调节的控制方法。然而,反步控制方法是基于模型的,不能确保PMSM系统在存在不确定性和外部扰动的情况下的鲁棒性[10]。滑模控制(sliding mode control,SMC)因其对干扰的鲁棒性、快速响应时间和易于实现而日益受到关注[11]。该控制方法主要通过其非连续切换项获得强鲁棒性能,然而不适当的切换增益将会引起系统抖振[12]。将SMC与扰动观测器相结合是提高基于SMC方法鲁棒性的一种有效方法。扰动观测器可以估计未知扰动(包括参数变化和外部扰动),并将其前馈给SMC,从而减少抖振[13]。非线性扰动观测器(nonlinear disturbance observer,NDO)因其易于实现并产生可靠的扰动估计,成为目前的主流扰动观测器技术[4]。然而,此类研究使用的NDO大都采用固定观测器增益,这可能导致观测器在某些关键场景下提供较慢的收敛速度,例如外部负载扭矩的突然变化[13]。

本文的主要目标是采用反步控制(Backstepping)和SMC结合的方法来设计一种反步滑模控制器(BSMC)用于位置跟踪控制。然而,由于反步方法的固定收敛增益,BSMC可能会在位置步长分布中引起大的过冲。为了解决这个问题,本文提出了一种包含自适应收敛增益的自适应反步滑模控制方法(ABSMC)。该方法,既可以将实际位置加速到目标位置,又可以减少过冲。此外,通过改进NDO的非线性观测器增益函数,可以估计参数不确定性和外部负载转矩扰动,并为ABSMC提供前馈补偿,保持ABSMC的鲁棒性,减少稳态误差。

1 PMSM数学模型

假定三相PMSM为理想电机,且满足:忽略电机铁心饱和;不计电机中的涡流与磁滞损耗;电机中的电流为对称的三相正弦电流。则PMSM系统在转子d-q参考系中的数学模型可以表示为[2]:

(1)

(2)

(3)

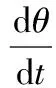
(4)

式中:id、iq分别为d-q坐标系下的定子电流,vd、vq分别为d-q坐标系下的定子电压,Ld、Lq分别为d-q坐标系下的定子电感,ω为转子机械角速度,θ为转子机械角度,P为磁极对数,Φ为电机永磁磁通,J为转动惯量,R为定子相电阻,B为粘滞摩擦系数,TL为负载转矩。

假设TL为未知,但在较小的采样间隔内变化缓慢。在实际操作条件下,电机经常会受到内部参数变化和外部扰动的影响。根据式(3),力学方程可以改写为:

(5)

式中:Jn和Bn分别是J和B额定值,并且J=Jn+ΔJ,B=Bn+ΔB。

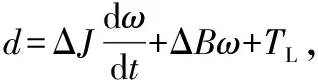
2 自适应反步滑模控制器设计

2.1 反步滑模控制器设计

为了便于控制器的设计,把PMSM系统式(1)～式(4)改写为式(6)～式(9)。

(6)

(7)

(8)

(9)

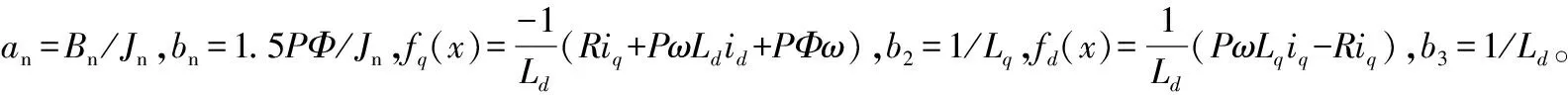
式(6)～式(8)用于构建q轴电流控制器(图1中的步骤1～步骤3),式(9)用于构建d轴电流控制器(图1中的步骤4)。

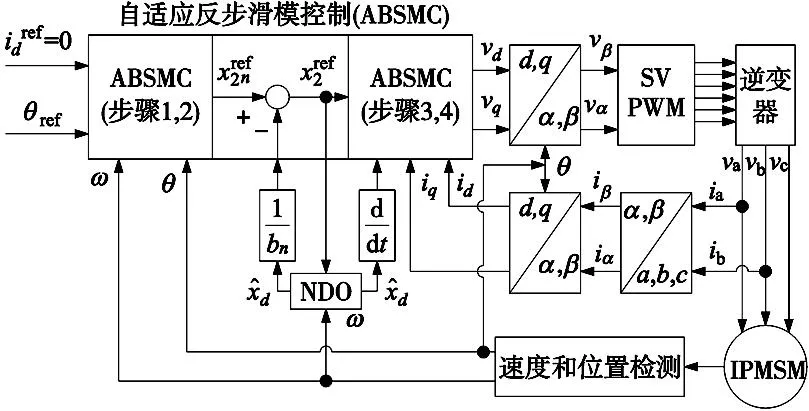
图1 基于ABSMC+NDO的PMSM控制原理图

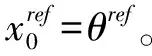
(10)

根据式(10),式(7)的虚拟控制输入被设计为:

(11)

式中:c0>0是渐近收敛速度的正常数。

(12)

(13)

然后可以将式(8)的虚拟控制输入确定为:

(14)

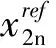
(15)

式(11)和式(15)中的正增益c0和c1表示反步控制器的收敛增益。如果这些增益较大,系统将具有更快的响应和优越的鲁棒性,但在阶跃信号中将发生较大的过冲。如果这些增益的值很小,系统将响应缓慢,过冲将减少。因此,在稳定时间和过冲之间存在权衡。这个问题将在2.3节中通过设计一个自适应算法来解决。

(16)

结合式(14)和式(15),式(16)可改写为:

(17)

滑动模块的恒定比例速率趋近律[13]设计如下:

(18)

由此得到的控制系统是渐近稳定的:

对e2求导可得:

(19)

式中:

(20)

结合式(7)和式(13),式(20)可改写为:

(21)

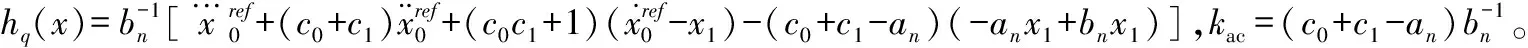
基于上述方程,vq可表示为:

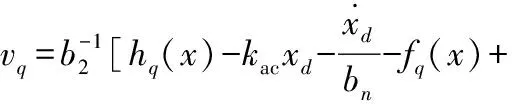
(22)

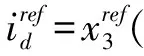
(23)

式中:α1>0,并且使用趋近律[13]得到:

(24)

并对式(23)求导得:

(25)

结合式(24)和式(25)可得:

(26)

2.2 非线性扰动观测器设计

非线扰动观测器(NDO)设计为:

(27)

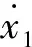
(28)

内部状态量z被定义为:

(29)

(30)

本文设计了一个非线性设计函数p(x1)为:

(31)

式中:L1和L2>0是常参数。该NDO采用了结合一阶和二阶状态变量的非线性设计函数p(x1)。将非线性函数p(x1)对x1进行微分得到:

l(x1)=L1+2L2x1sgn(x1)≥L1

(32)

观测器增益l(x1)被构造为满足观测器误差的全局指数稳定性的条件[13]。很明显,与文献[15]中使用的恒定增益L1相比,本文的l(x1)具有更大的幅度。非线性增益l(x1)可以提供更快的收敛速度,同时也减少了观测器误差[13]。

2.3 自适应反步滑模控制器设计

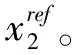
式中:f(e0)=λe-η|e0|0.5,η>0是实验确定的阈值。

3 仿真与结果分析

利用MATLAB/Simulink仿真软件对PMSM系统进行数值实验,仿真模型如图1所示,电机参数选取如表1所示。

表1 PMSM的参数值

控制器参数包括BSMC的参数c0、c1、k1、k2、k3、k4、α1;以及自适应算法的参数δ、λ、η。其中c0=c1,k1=k3,k2=k4。在恒定比例速率趋近律[13]下,参数(k1、k2)和(k3、k4)与vq和vd有关。首先,我们通过运行具有梯形速度运动阶跃信号但没有NDO组合的电机来配置BSMC参数。初始值c0和c1被选择为大于0.5an。根据实验结果确定了恒定比例速率趋近律[13]的因子k1、k2、k3、k4和α1,以便有效地减少系统抖振;然后,我们逐渐增加c0、c1,以将瞬态位置误差减小到可接受的值。在预先调整BSMC的参数后,将NDO与BSMC相结合,以减少电机系统中的扰动和不确定性的影响。添加NDO后,瞬态位置误差应减小。观测器增益L2=0,L1首先选择较小的值,然后L1逐渐增加以获得可接受的位置误差。类似地,在保持合适的L1的情况下,我们将L2配置为较小的值,并逐渐增加L2,以进一步减少稳态位置误差。在选择了BSMC和NDO的参数后,调整自适应增益(λ和η),从而调整收敛增益c0和c1。通过进行实验,我们得到λ的值在1～4范围内,η在0.1～2范围内时将得到更好的结果。阈值δ被配置为从一个小值开始,并逐渐增加,直到过冲减少。

(a) 位置跟踪 (b) 自适应收敛增益

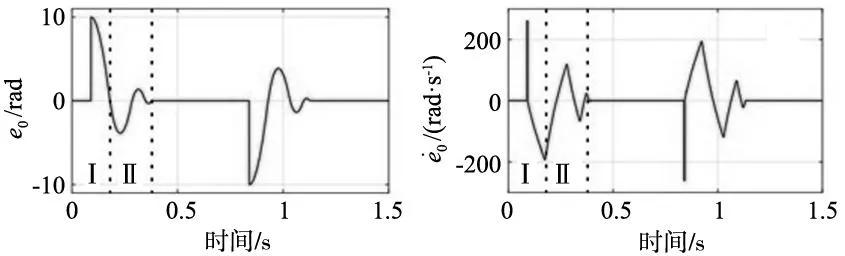
(a) e0 (b) e1

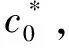
(a) e0 (b) e1

4 结论

本研究提出了一种基于ABSMC和NDO的提高PMSM系统位置响应的有效方法。ABSMC位置控制器包括BSMC和自适应收敛增益算法,BSMC是反步和滑模控制的结合,简化了控制结构,提高了位置跟踪的动态响应,当电机在当电机在梯形阶跃信号下运行时,使用自适应收敛增益算法来减少大的过冲位置响应;并用具有非线性观测器增益函数的NDO来估计参数和外部负载转矩的不确定性,将其用作ABSMC的前馈补偿。仿真对比结果证实了所提方法的有效性,表明该方法可以提高PMSM控制系统的整体性能,包括快速瞬态响应、小的稳态位置误差、减少过冲量和对未知扰动的鲁棒性。