基于熵增强混沌遗传算法的柔性作业车间调度*

李永湘,姚锡凡

(1.贵州工程应用技术学院机械工程学院,毕节 551700;2.华南理工大学机械与汽车工程学院,广州 510640)

0 引言

优质的作业车间调度是提高制造企业生产效率和竞争力的重要途径。现代制造企业的多目标柔性作业车间调度问题(multi-objective flexible job-shop scheduling problem,MFJSP)突破了传统作业车间调度问题(job-shop scheduling problem,JSP)中工序对应制造资源的唯一性约束[1]。在MFJSP加工任务中工件拥有多个备选加工路线,每道工序可有多个备选加工设备,且每道工序在不同加工设备上的加工时间可以是不相同的[2]。为了实现最优化作业车间调度,需要根据市场变化需求和企业生产实际情况,动态调整工件各道工序由哪台机器处理,达成多目标综合调度质量最优[3]。MFJSP问题模型更符合现代制造企业生产实践,但也扩大了可行解空间,已被证明是一个NP难题[4]。柔性制造生产实践过程复杂,给加工车间制定最优调度方案并有效组织生产提出了更高要求。为了在当前逆全球化复杂环境下存活并发展下去,如何以最低成本、最少时间和最低生产组织复杂度完成工件加工任务成为众多制造企业追求的目标。

国内外学者先后应用遗传算法、粒子群优化算法等智能算法求解JSP问题,取得了许多成果。其中,遗传算法求解复杂车间调度问题时潜力巨大,各种改进遗传算法为柔性作业车间调度优化提供了新思路。谢志强等[5]应用基于分枝定界和遗传算法相结合的混合优化策略实现多车间动态重调度。胡瑞淇等[6]研究了二进制编码遗传算法求解顺序柔性车间调度最优解。王佳怡、李博宇等[7-9]研究了不同的交叉变异算法。MARJAN等[10]设计了新的选择准则和基于机器的新交叉算子以解决算法早熟问题。XU等[11]提出了一种基于个体相似度的自适应交叉和变异操作。ATTIA、DANIAL等[12-14]研究了基于柯西变异、频率分析等基因种群改进法以提高遗传算法搜索能力。

上述研究从不同角度改进了遗传算法的交叉算子和变异算子等,但文献所提出的交叉算子产生的子代个体与父代个体之间相似程度高,全局搜索能力受限,对多峰函数易陷入早熟现象;优化过程中缺少对车间物流和调度复杂度的考虑等。本文将调度熵引入MFJSP模型计算调度复杂度,提高车间调度方案的综合调度质量,并提出熵增强混沌遗传算法求解MFJSP模型,用伯努利混沌映射和高斯云模型改进遗传算法邻域搜索功能,提高算法执行效率,最后通过应用案例和仿真实验验证所提出模型和算法的有效性。

1 多目标柔性作业车间调度问题建模

1.1 约束条件

MFJSP调度问题描述如下:N个工件(J1,J2,J3,…,JN)需在Q台机器(M1,M2,M3,…,MQ)上加工,每个工件的制造过程包含1道及其以上数量的工序;各工件的每道工序都有1台及其以上数量的可选加工机器;每道工序一旦开始加工就不可被中断;每道工序在不同机器上的加工时间可不同;每个工件的所有工序之间加工顺序是固定的;不同的工件之间加工无耦合关系,相互独立,加工优先级相同。因此,MFJSP中主要需考虑工序使用的机器和不同工件在同一机器上的加工顺序。MFJSP约束关系数学模型表示为:

(1)

PETjh+PWTj(h,h+1)≤PSTj(h+1)

(2)

(3)

(4)

(5)

(6)

式中:i表示机器编号,i=1,2,3,…,Q;Q表示总机器数目,Qjh表示第j个工件的第h道工序的候选机器总数,且Qjh≥1;j表示工件编号,j=1,2,3,…,N;N表示总工件数目,Pjh表示第j个工件的第h道工序,h表示工序编号,h=1,2,3,…,H;H表示总工序数目,Hj表示第j个工件的总工序数目,PSTjh表示第j个工件的第h道工序开始加工的时间,PETjh表示第j个工件的第h道工序加工结束时间,PETthreshold表示最大完工时间阈值,PWTj(h,h+1)为第j个工件的第h道工序与第h+1道工序之间的等待时间,MPTijh表示第j个工件的第h道工序在第i台机器上的加工时间,σijh为开关变量。

式(1)和式(2)表示同一工件的工序约束关系,只能在上一道工序完成后才能开始下一道工序。式(3)表示工件的完工时间约束关系,所有工件的最大完工时间不能超过调度方案的最大完工时间阈值。式(4)表示机器约束关系,同一个工件的同一道工序只能被一台机器加工。式(5)表示每个工件的制造过程包含1道及其以上数量的工序。

1.2 目标函数

为获得综合调度质量最优的调度方案,本文设定了4个目标函数为:

目标函数1:求最大完工时间的最小值。

(7)

各个工件最后一道工序的结束时间称为该工件的完工时间。调度方案中各个工件完工时间的最大值称为该调度方案的最大完工时间。最大完工时间越小可确保工件交货期,提高企业响应市场需求的敏捷度。

目标函数2:求最大机器负荷差的最小值。

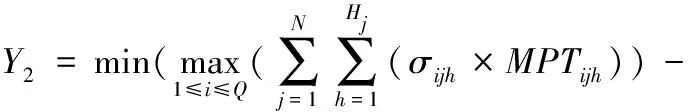
(8)

不同调度方案中各个机器的加工负荷各不相同。机器之间负荷差越小,则各机器负荷越均衡。机器负荷均衡有利于充分发挥所有机器的效能,并方便机器的统一维护管理。

目标函数3:求机器总负荷的最小值。

(9)

不同的调度方案中工序选择不同机器加工工件所用时间不同,导致机器总负荷不同。加工成本往往与总加工时间成正比关系,尽量减小调度方案的机器总负荷,有利于节省成本,降低能耗。

目标函数4:求调度复杂度的最小值。

调度复杂度通过调度熵来衡量。调度方案中单个工件的调度熵计算如下:

(10)

式中:SEj是第j个工件生产过程的调度熵,JSTjk是第j个工件在第k个状态下的持续时间,工件的状态主要包括从第一道工序开始至最后一道工序结束期间该工件的所有工序加工状态和相邻两个工序之间的等待状态;JMTj是第j个工件从第一道工序开始至最后一道工序结束所用的总时间,SNj是第j个工件从第一道工序开始至最后一道工序结束期间所经历的总状态数目。柔性作业车间调度复杂度等于调度方案中所有工件的调度熵之和,即总调度熵。总调度熵越小,则调度复杂度越小,工件制造可靠性越高,成功完成工件制造任务的概率越大。调度复杂度最小值计算公式为:

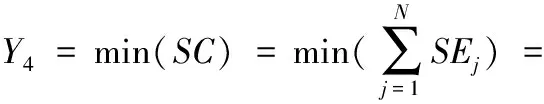
(11)

式中:SC表示调度复杂度,N表示调度方案中的总工件数目。

2 熵增强混沌遗传算法

为提高MFJSP调度问题寻优质量,克服传统遗传算法易过早陷入局部极值的问题,本文提出一种熵增强混沌遗传算法(entropy-enhanced chaotic genetic algorithm,ECGA)求解MFJSP模型。将伯努利混沌映射引入遗传算法,利用混沌运算的随机性、遍历性、非线性特点,改进选择算子,优化算法邻域搜索功能,应用高斯云模型改进交叉算子和变异算子,避免寻优过程陷入局部极值,提高算法执行效率。

2.1 基因编码

ECGA算法采用二进制编码方法建立遗传基因与调度方案的映射关系。在MFJSP调度问题中,一个工件Jj的加工过程由Hj个工序组成,每个工序Pjh可分配到Qjh个可选加工机器中的某台机器上完成。一个调度方案可以表示为具有N个染色体的染色体链,为基因种群中的一个个体。每个染色体对应一个工件。每个染色体具有Hj个基因片段。每个基因片段对应一个工序。基因片段中的每个基因表示可以完成该工序的候选加工机器。第j个染色体的第h个基因片段对应于第j个工件的第h个工序Pjh。每个基因片段本质是一个候选加工机器集M,它包含对应工序的多个候选加工机器。基因值为1时表示选择由该基因映射的加工机器来完成与其基因片段相对应的工序;基因值为0时表示未选择该加工机器。图1展示了一个MFJSP调度方案的ECGA基因编码,其中每个工件的加工被分解为若干个工序,每个工序对应一个候选加工机器集。

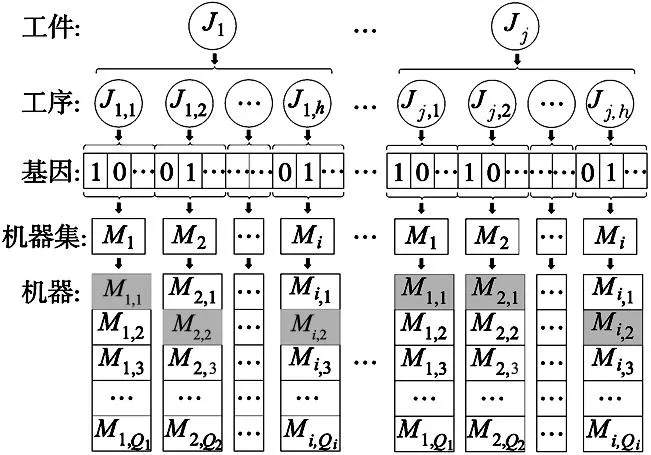
图1 基因编码示意图

2.2 选择操作

为了获得比传统遗传算法更好的优化效果,在选择操作中引入伯努利混沌映射公式,如式(12)所示。

(12)

C(t)=int(PS×B(t))+1

(13)

式中:λ为控制参数,PS为种群中的个体总数,B(t)表示第t次迭代后生成的伯努利混沌映射随机数,C(t)表示选择操作种群个体序号,int()为取整函数。伯努利混沌映射初始值设置为(0,1)区间内的均匀随机数。

ECGA采用二元随机锦标赛模式进行选择操作,步骤为:

步骤1:根据伯努利混沌映射公式生成2个随机数,从种群中选择对应序号的2个个体,比较其适应度,并将适应度最高的个体遗传给下一代种群;

步骤2:重复步骤1PS次,获得下一代种群的PS个个体。

2.3 交叉操作

ECGA引入高斯云模型改进交叉算子和变异算子,避免寻优过程陷入局部极值,提高算法执行效率。高斯云模型促使ECGA早期阶段有较大的交叉概率和变异概率来提高精英个体的出现概率,而在ECGA后期阶段有较小的交叉概率和变异概率,尽可能保持种群中的精英个体以加快全局收敛速度。交叉概率计算公式为:

(14)

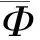
根据式(14)计算交叉概率Pc并执行交叉操作。如图2所示,ECGA使用切牌式交叉操作,扩展搜索空间,提高种群基因的多样性。切牌式交叉操作时,两个父代个体沿着位于相同位置的任意相邻两个基因片段之间的间隙被分成两个部分。第1个父代个体的前半部分与第2个父代个体的后半部分依序组合在一起形成新的子代个体;同时第2个父代个体的前半部分与第1个父代个体的后半部分依序组合在一起构成另一个新的子代个体。

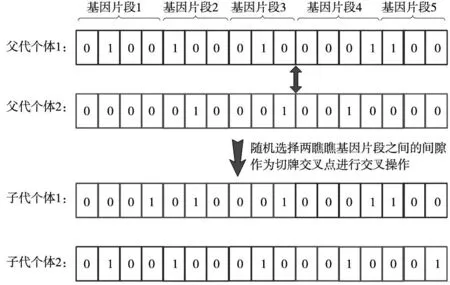
图2 切牌式交叉操作

2.4 变异操作

变异概率计算公式为:

(15)

式中:Pm是变异个体的变异概率,Pmmax是种群的最大变异概率,Pmmin是最小变异概率,Φ′是变异个体的适应度值,η3和η4是区间[0,1]中的常数,取η3=0.4,η4=0.8。

根据式(15)计算变异概率Pm并执行变异操作。如图3所示,ECGA使用两基因片段式变异操作方法,随机选择父代个体中的两个基因片段,将所选基因片段中的一个基因编码置1,其它基因编码置0,从而产生一个新的子代个体。

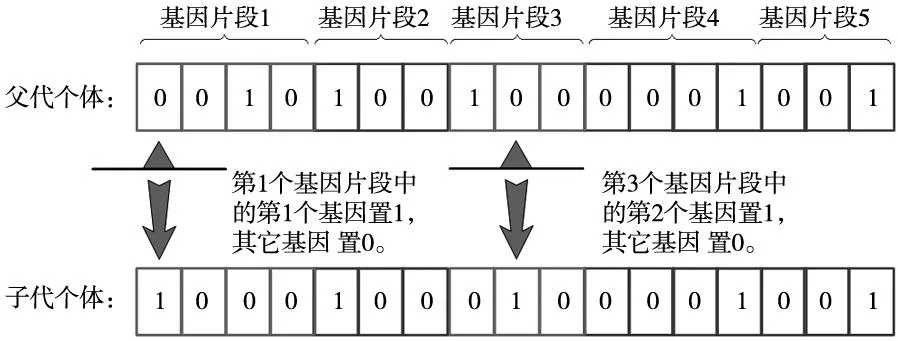
图3 两基因片段式变异操作

2.5 适应度函数构建

ECGA采用加权相对偏差来评估调度方案综合性能,并构建适应度函数。加权相对偏差是所有目标函数相对偏差的加权和,其计算公式为:

(16)

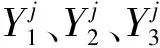
加权相对偏差越小,调度方案综合调度质量越好。根据式(16)设计ECGA适应度函数如下:

(17)

式中:f(j)是种群中第j个个体的适应度函数,Γ是足够大的正数。适应度函数越大,调度方案综合性能越好。

2.6 ECGA算法步骤

ECGA算法流程如图4所示,具体步骤为:

图4 ECGA算法流程图

步骤2:计算种群个体对应调度方案的4个目标函数值:最大完工时间、最大机器负荷差、机器总负荷和调度复杂度;

步骤3:计算种群中所有个体的加权相对偏差、适应度值,并计算最大适应度值、最小适应度值和平均适应度值。判断每个个体是否满足约束条件式(1)～式(5),如果满足约束条件,返回是,否则返回否;

步骤4:将种群中满足约束条件的每个个体适应度值f(j)与全局最优适应度值f(GOS)进行比较。如果f(j)>f(GOS),则用f(j)替换f(GOS),并用第j个个体替换全局最优个体GOS,从而得到新的全局最优个体和全局最优适应度值;

步骤5:计算伯努利混沌映射随机数,应用二元随机锦标赛模式进行选择操作;计算高斯云模型的期望值、云熵、超熵和标准差,求出不同个体的交叉概率和变异概率,并执行切牌式交叉操作和两基因片段式变异操作;

步骤6:检查算法是否达到终止条件。如果进化代数达到所设定的最大值或满足算法的其它结束条件,则停止算法迭代操作并输出结果;否则,转到算法步骤2。

上述算法中,步骤1功能是初始化种群,步骤2计算种群个体对应调度方案的4个目标函数值,其时间复杂度为T1=O(n);步骤2～步骤6实现算法循环迭代,当作业车间调度规模足够大时,忽略其它低次幂项式,可得总的算法时间复杂度为T2=O(n2)。

3 应用案例

以12个工件、3道工序、8台机器所构成的柔性作业车间调度问题M8J12P3[10]为例说明MFJSP模型和ECGA算法应用过程。用户选择在8台机器上加工12个零件,每个工件有3道工序,且需遵循工序先后顺序加工。8台机器分别表示为M1、M2、M3、…、M8,12个工件加工任务分别表示为J1、J2、J3、…、J12,Pj,h其表示第j个工件的第h道工序,各工序在机器上的加工时间(单位:h)如表1所示。

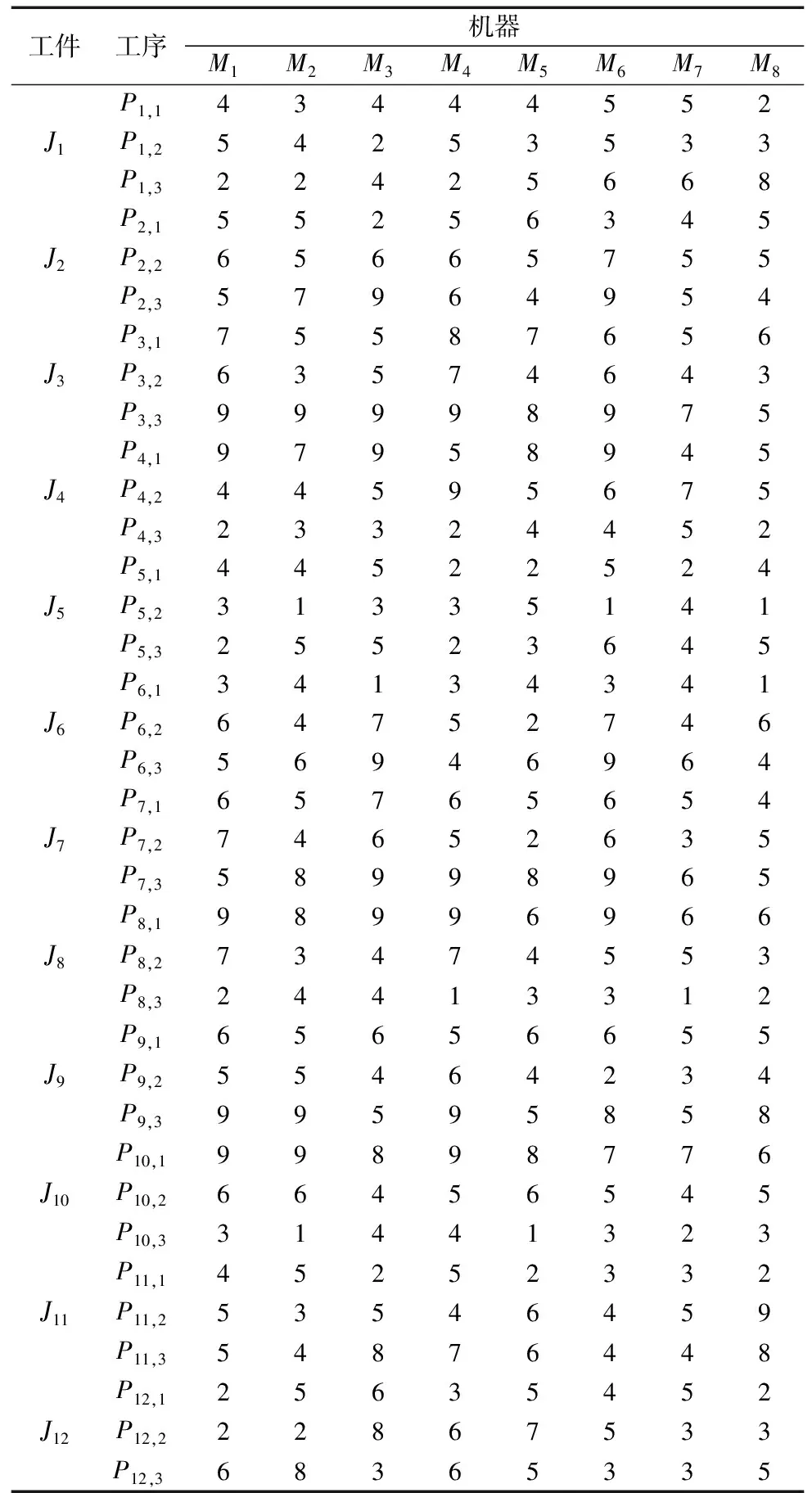
表1 M8J12P3加工参数表

选用MATLAB R2019a编写并运行ECGA算法程序。设定最大完工时间阈值PETthreshold为72 h,种群规模PS为80,最大进化代数MG为300,Г=99。4个目标函数的权重系数分别设置为δ1=δ3=0.3,δ2=δ4=0.2。运行ECGA算法程序10次,取其中最优调度方案如图5所示,其最大完工时间为15 h,最大机器负荷差为1 h,机器总负荷为113 h,调度复杂度为15.928。机器M1上的加工顺序为:P12,1、P12,2、P4,2、P4,3、P7,3;机器M2上的加工顺序为:P3,1、P11,2、P8,2、P1,3、P10,3;机器M3上的加工顺序为:P2,1、P6,1、P11,1、P12,3、P1,2、P10,2;机器M4上的加工顺序为:P9,1、P5,1、P5,3、P6,3、P8,3;机器M5上的加工顺序为:P8,1、P6,2、P7,2、P2,3;机器M6上的加工顺序为:P10,1、P5,2、P9,2、P11,3;机器M7上的加工顺序为:P4,1、P2,2、P9,3;机器M8上的加工顺序为:P7,1、P1,1、P3,2、P3,3。

4 算法比较分析

在相同最大进化代数的情况下,将ECGA算法、粒子群优化算法(PSO)[15]、人工蜂群算法(ABC)[16]和标准遗传算法(SGA)[17]用于解决相同的柔性作业车间调度问题M8J12P3。SGA算法的参数设置与ECGA算法相同:种群规模为80,最大进化代数为300。PSO算法的参数设置如下:粒子群个数为80个,迭代次数为300,个体学习因子和群体学习因子各取值为2,惯性因子取值为0.2。ABC算法的参数设置如下:种群规模为80,迭代次数为300。上述4种算法各运行10次取最优值,得到的结果如表2所示。调度方案矩阵中第1行～第8行依次表示第1台～第8台机器的加工顺序。4种算法所求调度方案的机器总负荷值接近相等。但与SGA、PSO、ABC所求调度方案相比,ECGA求得的调度方案具有更小的最大完工时间、最大机器负荷差和更好的适应度值。与其它3者比较,ECGA所求调度方案的调度复杂度较大,说明在降低调度方案的最大完工时间和最大机器负荷差时,会增大调度复杂度。追求最优综合调度质量不可兼得各个单目标函数的最优值。实验结果表明,对于解决柔性作业车间调度问题,ECGA比SGA、PSO和ABC具有更快的收敛速度和更好的全局搜索能力,如图6所示。ECGA优化结果具有最佳的综合调度质量,有助于企业提高生产效率和降低成本。

表2 几种算法的M8J12P3调度问题寻优结果比较

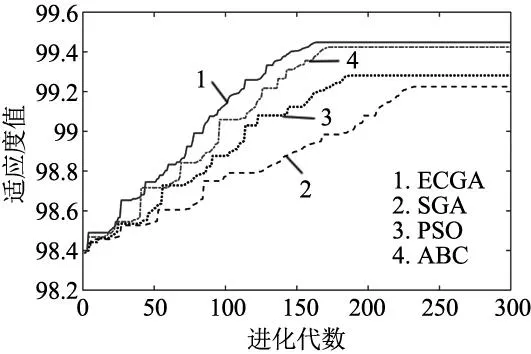
图6 几种算法的M8J12P3调度问题寻优迭代曲线

5 结论

研究了多目标柔性作业车间调度数学模型及其求解算法。首先建立了考虑最大完工时间、最大机器负荷差、机器总负荷和调度复杂度的 MFJSP优化模型。然后提出一种改进的熵增强混沌遗产算法求解MFJSP模型。应用伯努利混沌映射改进选择操作,用高斯云模型改进变异算子和交叉算子,提高了算法全局寻优能力和搜索效率,使用切牌式交叉操作和两基因片段式变异操作来扩展搜索空间,提高种群基因的多样性,避免了传统遗传算法易早熟缺陷。最后以M8J12P3调度问题为例验证了ECGA算法的有效性。与SGA、PSO和ABC相比,ECGA具有更快的收敛速度和更好的全局搜索能力,有助于企业获得综合调度质量最优的车间调度方案,提高生产效率和降低成本。案例研究结果显示在降低调度方案的最大完工时间和最大机器负荷差时,会增大调度复杂度,追求最优综合调度质量不可兼得所有单目标函数的最优值,说明MFJSP优化模型具有重要的应用价值。