翘曲板材三维重构及智能化压平的建模研究

马 宝，马晓宝，兰 媛，任玉成，刘云飞，马彦芝，王荣军，江连运

1) 太原理工大学机械与运载工程学院，太原 030024 2) 太原理工大学先进金属复合材料成形技术与装备教育部工程研究中心，太原030024 3) 中国重型机械研究所股份有限公司，西安 710018 4) 太原科技大学机械工程学院，太原 030024

中厚板广泛应用于军工装甲、石油化工、船舶桥梁、核电装备等领域[1]. 随着控轧控冷等轧制工艺的创新发展以及板材厚度和宽度的不断增加，中厚板轧制过程变形不均匀、内应力严重的问题变得突出[2]，在热处理过程容易发生弯曲、瓢曲等变形，造成平直度指标下降，下游产业对厚板平直度要求严苛，通常都需要进行矫直[3]. 热辊式矫直钢板厚度一般限制在100 mm以下，冷辊式矫直钢板厚度不超过40 mm，对于厚度超过100 mm的特厚钢板以及翘曲严重的厚板通常需要进行压平矫直[4]. 传统压平主要基于人工经验进行作业, 压平过程一般分为上料、翘曲程度检查、送料、放置垫铁、压平和出料6个阶段，如此反复多次，直至将整块钢板矫平为止[5]，整个过程主要依赖手工控制或者通过压力和位移传感器进行半自动控制.

为提高压平矫直的精度和质量，江连运等[6]建立了宽厚板压力矫平模型进行了有限元仿真对比，在假定初始曲率情况下，得到了压平力和压头行程等参数. 赵军等[7]建立了大口径直缝焊管的纯弯曲过弯矫直等价模型，进行了实验验证. 余忠华等[8]基于平面弯曲变形和应力–应变模型建立了导轨矫直曲率和压下行程计算模型，有限元验证结果表明模型精度较高. 针对人工设定压下不准确、需要多次反复压平的问题，孙登月等[9-10]提出了多点反弯曲工艺、多点柔性压力矫直工艺，实现了反弯压平矫直工艺参数的计算. 汝文弟等[11-12]]提出柔性支撑交错布置的四点压平工艺，建立了四点矫直模型，修正了反弯量计算模型，结果显示四点弯曲具有更加优良的压平效果. 压平工艺中垫铁放置是影响压平效率的另一个关键难题，韩兴等[13]设计了一种液压驱动的垫铁布置方案，通过在底座预布置矩形分布、液压驱动斜楔配合块来实现垫铁的自动化布置. 板坯的初始翘曲程度是决定板坯反弯曲率、压下量、压下间距计算精度和效率的重要前提，是影响中厚板压平质量和效率的关键. 上述研究集中在已知初始曲率条件下提高压下工艺参数计算精度和控制效果，缺乏翘曲板材特征识别及相关后续工艺建模的探究.因此，研究翘曲板材的三维重构和初始翘曲曲率识别对提高精整压平质量和效率意义重大.

机器视觉技术随着人工智能技术的进步得到快速发展，为板材智能化压平控制提供了技术方案. 在冶金行业，机器视觉已经用于工件的尺寸测量和缺陷识别分类等，例如热轧精整物料跟踪[14]、精整过程尺寸自动化测量[15]、热轧跑偏测量[16]、热轧板坯镰刀弯识别和测量[17]、钢板表缺陷识别[18]等.杨恒等[19]基于双目多组线阵相机，使用多种滤噪算法以及粒子群优化算法建立多目标优化模型，研发了中厚板智能剪切系统并成功应用于莱芜4300 mm产线，提高了剪切质量和生产效率. 于浩等[20]搭建激光扫描系统对无缝钢管生产线上的工件进行扫描，获取其表面轮廓的点云数据，训练点云深度网络pointnet建立了无缝钢管表面缺陷识别模型.

在工业应用中，二维视觉算法主要是工艺参数确定以及通过数字图像处理完成目标缺陷检测，三维机器视觉通常是三维重建算法的应用基础[21-22]. 按照光学与视觉理论，机器视觉技术可以分为主动视觉和被动视觉两大类[23-24]，其中被动式方法的主要核心在于分析获取目标图像序列中的各种信息，这类方法成本较低，适用的场景较多，例如赵畅等[25]使用运动恢复结构(Structure from motion，SFM)算法重建钢板表面的点云数据，基于区域增长的点云信息算法从钢板表面中分割缺陷点云数据并进行分类，实现了板材表面缺陷检测. 但被动视觉技术进行物体的三维重建时，物体中的细节微小特征重建困难，需要物体具有明显的特征点. 而主动式三维重建技术是直接对场景或对象进行光学扫描[26]，完成重建，该类方法能得到物体表面的详细信息，重建精度较高且速度较快. 闫杰琼等[27]利用三维激光扫描设备获取航空发动机外形实测点云，提出的一种基于深度学习的点云保特征去噪方法，为后续重建曲面提供了高质量的点云模型. 曾凯等[28]使用基于线结构光点云三维重建的方法对内外形状不规则的弯曲管工件进行测量，检测精度高、用时短，有良好的工业应用场景. 不同于具有较多特征点的复杂结构，翘曲板材主要特征为光滑曲面，特征点相对较少，基于被动视觉技术一般难以准确实现重构.

为实现板材压平过程的智能化控制，本文将采用结构光相机获取翘曲板材表面点云，研究点云处理方法，以点云数据拟合重构翘曲板材的三维曲面. 在获取的三维曲面的基础上，建立三维曲面翘曲曲率计算模型，优化确定压下点和垫铁支点的位置，计算压下力和压下位移，最后采用有限元模型和实验对理论计算结果进行验证.

1 液压压平工艺改进方案

宽厚板液压压平机由主机本体、托辊等辅机设备、液压系统、润滑系统和电气系统组成，主要针对厚度30 mm以上的厚板进行压平矫直. 压头系统由横移小车带动进行横移动作，主液压缸推动压头通过垫板对板材施加压力，按照三点弯曲的原理对板材进行矫平作业[29]. 因而板材初始翘曲分布、压下位置点、垫铁位置与压下位移是影响压平质量的关键工艺参数，压下力是优化压下工艺、保障设备安全的重要参考. 传统作业过程一般需要设备操作者和台下操作工密切配合，操作工根据经验进行垫铁布置，指导压下位置及压下行程控制，因而压平质量在很大程度上取决于工人的熟练度和专业程度，存在很大的调整误差和效率波动.

为避免人工造成的压平质量和效率不高问题，提高压平的智能化水平，本研究采用结构光相机获取翘曲板材的点云数据. 如图1所示，板材在运输辊道上的托辊和移送推头作用下断续进入压头工作范围，通过在压平机入口竖直放置的相机，扫描获取翘曲板材轮廓点云信息，从而实现以机器视觉代替人工. 然后对点云数据进行处理，拟合得到翘曲板材三维轮廓函数. 由于压平机坐标系和相机坐标系的相对位置关系固定，已知翘曲板材轮廓在相机坐标系的分布，就可以得到平移后的翘曲板材特征相对压平机坐标系的分布，进而为压平作业提供板材初始翘曲轮廓信息. 传统压平模型普遍基于二维平面理论，在已知翘曲线曲率的基础上，给定垫铁间距下计算压下位移和压下力，现场操作普遍基于经验给定相关参数. 结构光视觉相机可以实现板材翘曲分布的精准识别，但翘曲板材本质是一个典型的三维曲面，如何基于重构的三维轮廓求解过压下点的翘曲曲率是不同于传统二维平面压平理论所面临的新挑战. 基于精确的三维轮廓可优化得到合理的压下位置点、垫铁位置，进而可以提高压下位移和压下力计算的精度，避免传统人工经验造成的误差，实现压平过程的智能化控制，提高压平质量的一致性和压平的效率. 为实现上述目标，本研究以实验样板进行了智能化压平过程的建模以验证方法的可行性，技术路线如图2所示.

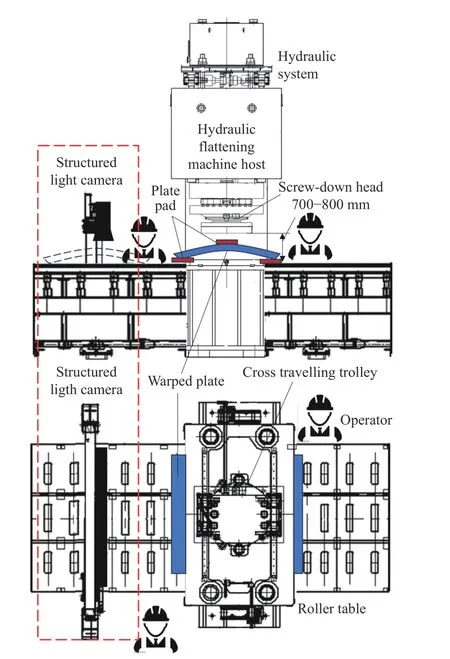
图1 压平工艺改进方案Fig.1 Improved plan for flattening process

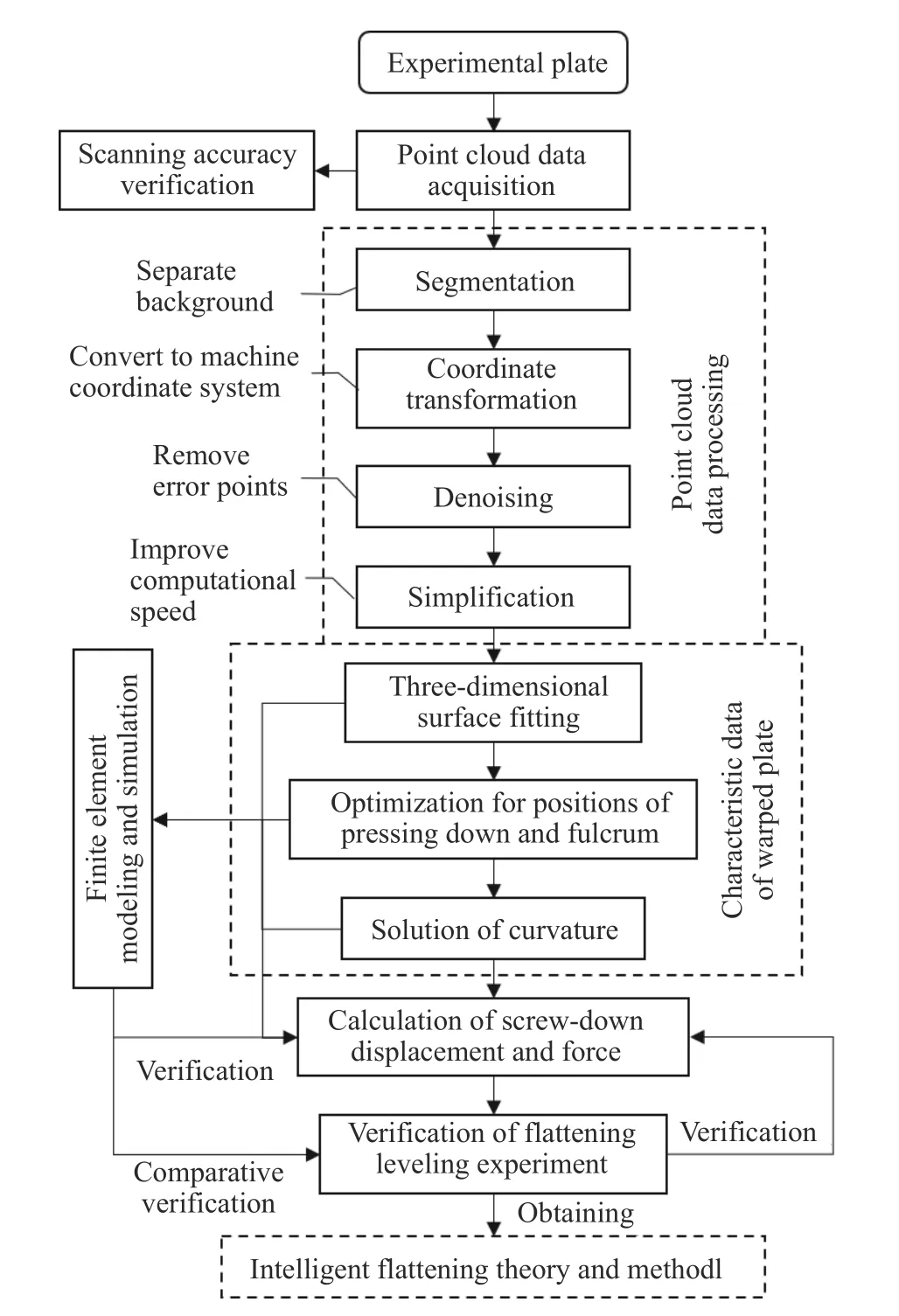
图2 智能化压平建模研究技术路线Fig.2 Technical route for intelligent flattening modeling

2 基于结构光技术的翘曲金属板点云获取和处理

为实现压平矫直全流程的建模和实验研究，选取铝板材为研究对象. 板带宽和长均为b=500 mm，厚度δ=5 mm，初始翘曲形态见图3(a)和(b)所示，宽度范围内板材上表面初始翘曲高度大约16.5 mm，利用结构光相机获取的初始点云扫描结果见图3(c).

图3 翘曲铝板材. (a)视图1; (b)视图2; (c)扫描点云Fig.3 Warped aluminum plate: (a) view 1; (b) view 2; (c) scanned point cloud

为评价扫描数据的准确性，采用置信图法进行精度评估. 置信图的像素值是相机和被测翘曲板材表面的实际距离与结构光解码后点云z坐标的差值，每个像素的测量误差被映射成颜色：误差为零的点是黑色，误差超过1 mm的点是白色，误差在0～1之间的点将有一些灰色的阴影. 如图4所示，扫描识别区域的平均像素值为0.51 mm，即平均识别偏差不超0.6 mm. 相比板材翘曲程度和板面尺寸而言，扫描误差完全在板材压平控制的精度范围以内.

图4 翘曲板材扫描置信图Fig.4 Confidence map of the scanned warped plate

2.1 点云分割

为便于进行后续的曲面拟合，需要对基于结构光相机获得的点云数据进行预处理. 点云分割是点云处理技术中的一项关键技术，由于在扫描中背景对象的存在不利于对目标点云的后续处理，因此需要将目标点云与其他点云对象分割. 点云分割方法主要分为基于边缘、区域增长、基于深度学习、基于聚类、基于模型等分割方法.

基于模型的分割方法是通过分析点云数据的几何形状、拓扑结构获取点云数据的特征，将点云数据分割成多个特征子集. 本文使用的M估计样本一致(M-estimate sample consensus，MSAC)算法从离散点云中检测和拟合平面、球体、圆柱体、圆锥体、圆环面等几何特征，该算法具有较强的鲁棒性. 由于地面点云对象点云数目较多，且噪点比例少，适合作为拟合平面算法的内点，所以使用拟合平面的模型算法进行点云分割. 该方法设置的关键参数为点到平面的最大距离，考虑到铝板材厚度为5 mm，本文中设置距离阈值参数为4 mm，这样可以保证翘曲板材点云对象作为地面点云拟合平面模型算法的外点，从而将原始点云分割为地面点云和板材点云对象，分割结果见图5.

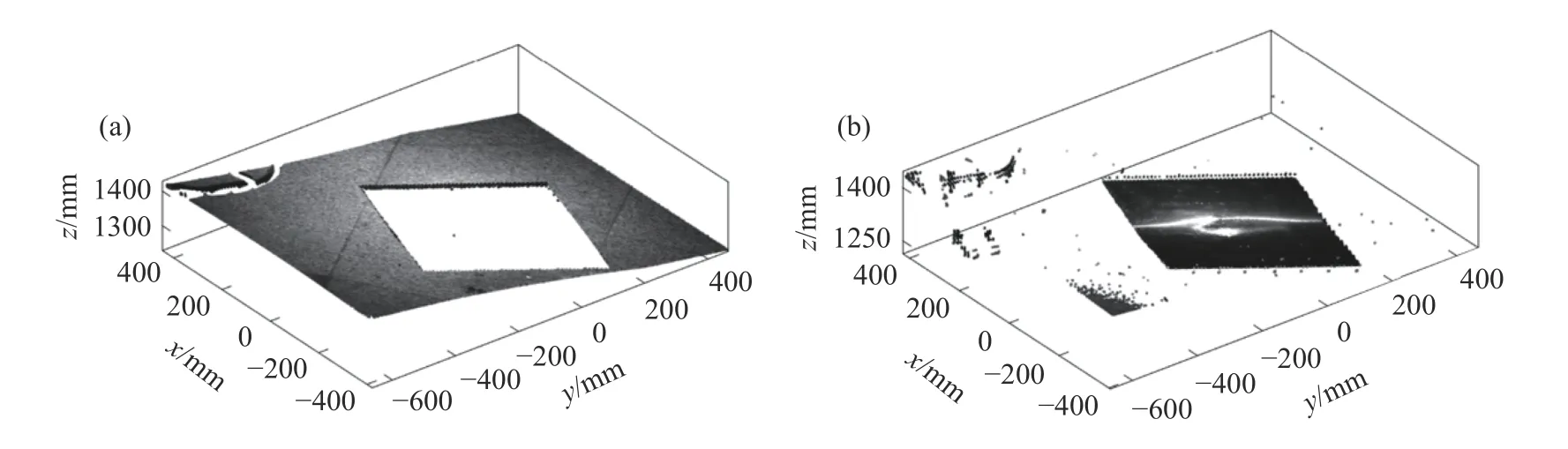
图5 翘曲板材分割后的点云. (a)地面点云; (b)板材点云Fig.5 Point cloud after segmentation of the warped plate: (a) point cloud of the ground; (b) point cloud of the plate

2.2 点云坐标系转换

水平放置结构光相机进行扫描时，由于结构光相机中的传感器以相对于传感器本身的特定角度安装，机器坐标系的x–y平面与翘曲板材的相对位置任意，扫描得到的板材表面点云数据处于机器坐标系的任意空间位置，不利于后续的去噪处理和曲面拟合，进行点云三维空间坐标系转换便于三维翘曲曲面的极值点优化，同时为准确得到压平机坐标系下板材三维翘曲轮廓的分布奠定基础. 坐标系位姿转换关系为：

为获得坐标转换矩阵的平移向量，将目标点云边界轮廓的中心P0=(x0,y0,z0)变换成为新坐标系原点，则可得变换矩阵中的平移列向量为Tr=[-x0-y0-z0]T. 为此，需要通过提取边界轮廓点进而得到几何中心P0=(x0,y0,z0). 目标点云轮廓即为图6(a)所示的地面点云模型的轮廓边界，采用点云库中的alpha-shapes平面点云边界特征法提取边界轮廓. 该方法的原理是通过假定一个半径为ra的圆绕待提取点云滚动，当该圆的半径足够小时，则点云边上的每一点均为边界轮廓点；当半径设定为合适的值时，就能够获得较为平滑完整的边界轮廓. 在本模型中设定半径ra= 5 mm，提取结果如图6(b)所示，结合目标点云原始坐标系XOY内的坐标范围限定，可确定内边界轮廓点云.

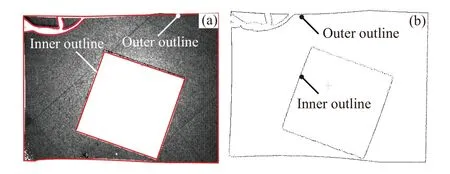
图6 地面点云. (a) 边界轮廓示意图; (b) 提取的边界轮廓点云Fig.6 Ground point cloud: (a) schematic of the boundary outline;(b) extracted point cloud of the boundary outline

在获取内轮廓边界后，通过式(2)计算点云模型的几何中心P0=(x0,y0,z0)为目标坐标系的原点：

式中，m为内边界轮廓点云的点数；xi、yi、zi为内轮廓点云坐标. 由于目标板材近似为矩形，为使变换后的x轴平行于板材边缘，该x轴上点Px=(xxx,yxy,zxz)的取值满足内边界轮廓点云模型中的点与原点P0距离最小，如图7所示.

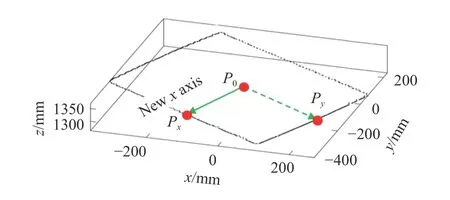
图7 目标坐标系原点和新x轴分布示意图Fig.7 Schematic of the target coordinate system origin and new x axis

按照式(3)和(4)，将Px与原点P0组成的新x轴上的向量单位化，获得新x坐标轴的单位向量rx：

则

将分割后的地面点云对象拟合平面方程，获得平面法向量ng=[nxnynz]T，按照式(5)和(6)单位化后得到平面z轴在机器坐标系的方向向量rz：

设目标坐标系y轴上的一点为Py=(xyx,yyy,zyz)，与原点P0组成y轴上的方向向量，该向量ry=[ryx,ryy,ryz]T满足：

得到坐标转换矩阵：

点云坐标系转换结果见图8.

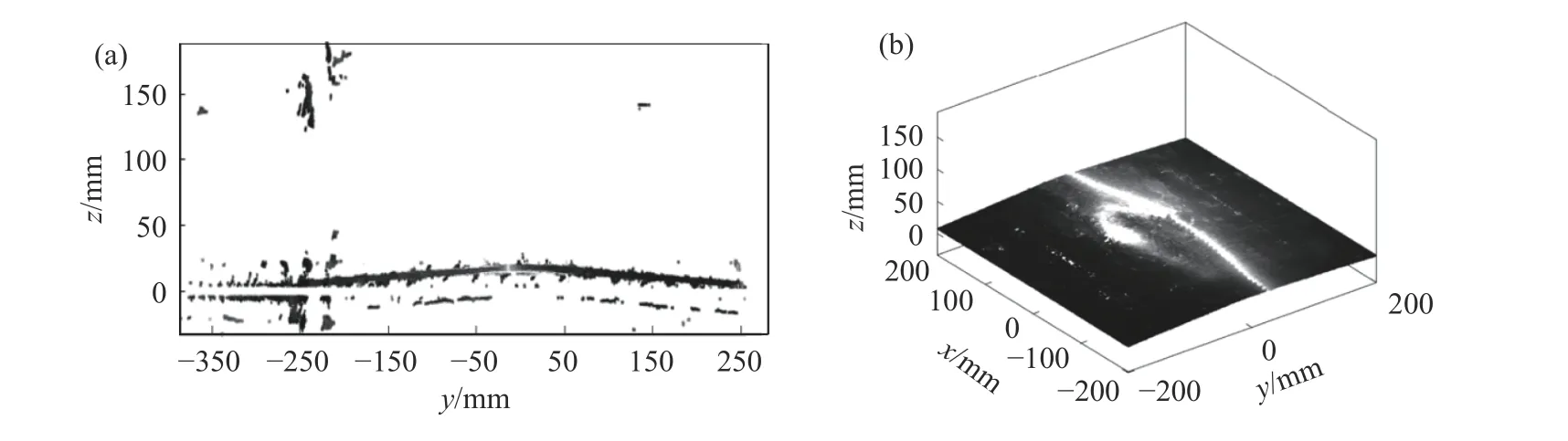
图8 翘曲板材坐标转换结果. (a)正视图; (b)轴侧图Fig.8 Warped plate coordinate transformation: (a) front view; (b) axonometric view

2.3 点云去噪

环境光照条件、扫描对象表面材质以及采集精度和采集方式等因素，会影响结构光的解码准确性，进而产生较多的噪点. 为了便于后续的点云处理和压平参数的精确计算，需对点云进行滤波处理. 由于翘曲板材特征简单，板面光洁，图幅空间较大，反光对解码的影响最大，噪点呈现区域高度和宽度偏离特征，部分噪点表现出局部孤立小区域离群点特征，适用于采用条件滤波器和基于距离的去噪方法进行去噪处理.

翘曲板材点云坐标系进行空间变换后，几何中心位于坐标原点，且轴向与板边平行，采用条件滤波器时，长度和宽度方向点云的x和y坐标值不在集合则认为是噪点；在高度方向，当点云的z坐标值不在集合z∈[0，Zmax]则认为是噪点，其中Zmax为基于上游激光检测或者人工检测板材翘曲最大值.

基于距离的去噪方法去除空间偏离噪点，约束条件如式(9)：

式中，kz为近邻点数；dz为设定去噪距离；P为点云任意点；Pi为P点的周围点. 任意点P到周围点Pi的距离平均值Distmean大于设定距离条件dz则认为噪点，约束条件和去除效果见表1.

表1 基于距离的翘曲点云去噪Table 1 Point cloud denoising of the warped plate based on distance

2.4 点云精简

去噪后翘曲板材点云对象较为完整，但点云数量较多，影响后续分析计算效率，需进行点云精简. 点云精简的方法主要分为均匀下采样、随机下采样、空间下采样、非均匀体素下采样等方法. 由于翘曲板材点云分布呈现空间为保证点云形貌分布规律大致不变，使用不同尺度的空间下采样方法对点云进行精简. 采样点稀疏原理如式(10)所示：

式中，dJ为给定的空间尺度. 当目标点P与周围任意点Pi的距离小于设定距离dJ，则舍去目标点. 当空间尺度dJ分别取0.7、1和1.5 mm时，点云精简效果如图9所示. 可见随着尺度增大，点云密度明显下降，按照空间尺度dJ=1.5 mm精简点云，数据量从初始未降采样的727308个减少到87644个，点云精简率达到87.9%.

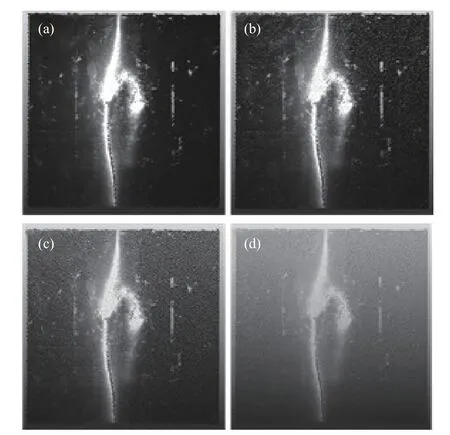
图9 翘曲板材空间下采样前后的点云. (a)未降采样; (b) dJ=0.7 mm;(c) dJ=1 mm; (d) dJ=1.5 mmFig.9 Point cloud of the warped plate before and after spatial subsampling:(a) no subsampling; (b) dJ=0.7 mm; (c) dJ=1 mm; (d) dJ=1.5 mm

3 翘曲板材三维曲面重构和曲率求解

3.1 曲面拟合

常规板材翘曲面呈现平缓的光滑分布，但曲面的曲率是变化的，为此需要采用高次型方程进行曲面拟合. 使用非线性最小二乘法对点云进行多项式函数拟合，双k次多项式函数表达式如(11)所示，曲面拟合结果见表2.

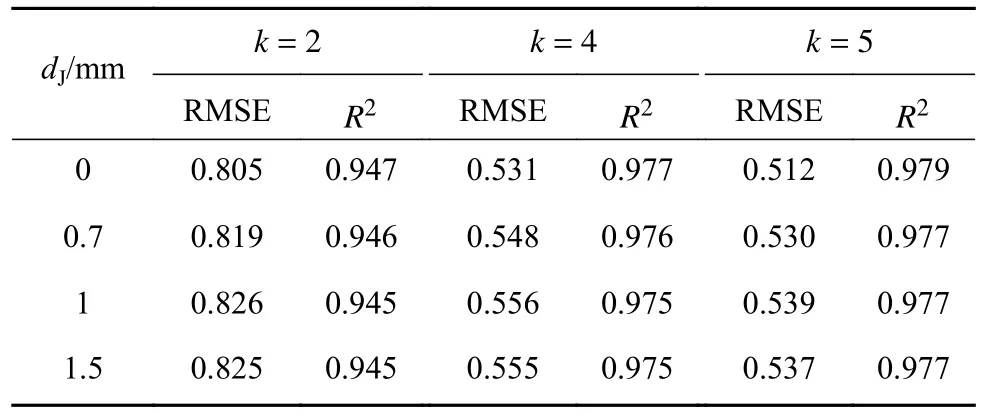
表2 不同方法拟合曲面指标Table 2 Fitted surface indexes under different methods

式中，k是拟合多项式最高次数；Ci，j–i是多项式系数；x、y和z是被拟合点云数据空间三维坐标值.以原始点云为数据源以及按照空间尺度dJ分别取0.7、1和1.5 mm的空间下采样方法精简后的点云为数据源进行曲面拟合，得到的双k次多项式曲面的均方根误差RMSE和调整决定系数R2. 由表2拟合结果可知，随着空间采样距离的增加，拟合的效果有降低的趋势，但相差不大，综合点云精简率，选择1.5 mm空间下采样精简点云作为最终数据，以双5次曲面方程进行曲面重构，最终绘制的翘曲板材点云以及拟合曲面如图10所示，拟合精度较高.

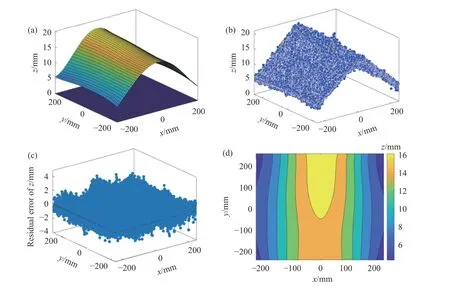
图10 基于翘曲板材点云数据拟合的曲面. (a) 拟合曲面图; (b) 点云图; (c) 残差图; (d) 等高线图Fig.10 Fitted surface based on the point cloud data of the warped plate: (a) graph of fitting surface; (b) point cloud; (c) residual plot; (d) contour map

3.2 压下位置点与垫铁支点位置的确定

常规压平建模研究一般是已知二维平面翘曲曲线的曲率进行工艺参数计算，而基于结构光视觉的翘曲板面重构后得到一个三维曲面方程，如何基于三维曲面方程获得初始翘曲曲率、曲面极值点和垫铁位置点等是确定工艺参数的难点.

实际压平机压头较大，压平过程的实质是以翘曲板材最高点为压下作用点，以局部低点为支点进行压平作业，因而优化求解三维曲面方程最高点为压下位置点，以局部低点为垫铁1的位置点. 建立极大值点优化求解条件，则曲面方程的最大值点(x0,y0)对应曲面方程的局部最大值hmax，满足式(12)：

令两个垫铁位置大致关于压下位置点对称分布，以局部最小值点(x1,y1)作为垫铁1(x1,y1)的位置点，该位置点与最高点间距要满足压平所能修正的最大初始平直度（Fs）以及大于垫铁宽度Bs同时小于压平机工作台最大长度Lws，具体约束条件如下：

压下过程要求两垫铁和压下位置点共面，且该面为一个竖直平面π. 因此，根据垫铁1位置点和压下位置点可以确定竖直π平面所在位置. 设竖直π平面的法向量为np=(npx，npy)，cp为π平面的另一系数，则π平面方程如式(15)所示：

令垫铁2的位置点(x2,y2)与垫铁1的位置点关于压下点对称且在曲面上，同时该点既位于π平面上，则可建立式(16)所示约束条件进而确定垫铁2位置点(x2,y2)：

3个目标函数中变量取值需要同时属于Ψ为点云的数据集，满足式(17)约束：

可以得到压下位置点间距：

按照上述优化原则，最终确定的压下位置点和垫铁位置点结果见表3.

表3 翘曲板材支点与压下点位置Table 3 Positions of fulcrums and screw-down

3.3 翘曲三维曲面曲率求解

传统二维压平建模研究，普遍是基于明确的曲率进行压平工艺参数的计算，然而三维曲面有无数条曲线组成，如何确定三维曲面的曲率成为基于视觉重构翘曲曲面压平建模的关键. 根据微分几何理论中的曲面论知识，曲面的法曲率为曲面第二基本型与曲面第一基本型的比值. 对曲面S:z=f(x,y)，令曲面内的向量rS={x,y,f(x,y)}，则三维曲面上任意点切向量为υ=rSxdx+rSydy，单位法向量为，其中rSx={1,0,zx}、rSy={0,1,zy}为一阶偏导数，则υ=(dx,dy,dx·zx+dy·zy)，nS=，曲面的第一基本量：

曲面的第一基本型：

曲面方程的二阶偏导数为rSxx=(0,0,zxx)，rSxy=(0,0,zxy)，rSyy=(0,0,zyy)，则曲面的第二基本量为：

曲面的第二基本型：

如图11所示，根据微分几何理论，过三维曲面最高点(x0,y0)，且切向量υ=(dx,dy,dx·zx+dy·zy)位于π平面内翘曲线的原始曲率(法曲率)如式(23)所示：

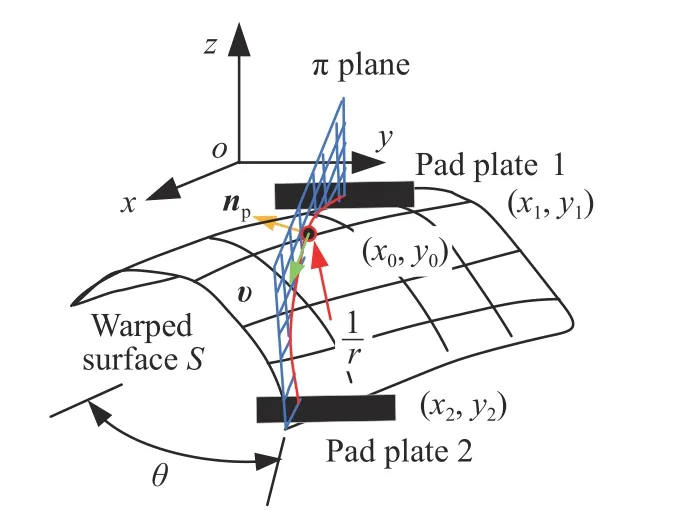
图11 法曲率与π平面和翘曲曲面关系示意图Fig.11 Schematic of the relationship between normal curvature and π plane and warped surface

式中，θ为π与xoz平面的夹角；tanθ=. 由于切向量υ位于竖直π平面内，因而竖直π平面的法向量np和切向量υ互相垂直，则υ·np=npxdx+npydy=0，因而可得：

将式(24)代入式(23)可得过压下点和两垫铁位置曲线的翘曲曲率，为后续压下位移和压下反力计算提供板面初始翘曲曲率参数.

3.4 压平工艺参数的计算

实验对象材质是1060铝板，厚度δ=5 mm，弹性模量E0=70 GPa，铝板材压平过程发生塑性变形，变形对强化影响较大，强化模量取E1=20 MPa，屈服极限σs≈40 MPa. 根据三点弯曲矫直理论[30]，采用上述优化确定的垫铁支点距、支点距间的翘曲高度、翘曲曲率等，分别计算考虑材料强化和不考虑材料强化两种状态下的平均压下力与压下位移如表4所示. 考虑到变形程度对实验用1060铝板的加工硬化影响较大，实际采用考虑材料强化的模型进行模拟和实验.

表4 理论计算压平工艺参数Table 4 Theoretical calculation parameters of the flattening process

4 有限元模拟

以板材翘曲高度方向为z轴，以板材宽度方向为y轴，以板材轧制方向为x轴，建立有限元仿真模型. 简化模型由上压头、两个垫铁以及翘曲板材所构成，翘曲板材为弹塑性体，上压头和垫铁部件均设置为刚体，为与实验对照，翘曲板材的材料属性与实验用1060铝合金板一致. 翘曲板材使用六面体单元，类型C3D8R划分网格，共70000个单元. 矫直过程，限制板材宽度边缘节点在板宽度方向位移，上压头刚体在水平面x和y方向进行约束，不能旋转，只保留高度方向的位移自由度；垫铁刚体完全固定；将上压头、两个垫铁与翘曲板材的三对接触均设置为“硬”接触. 载荷是通过给定上压头在z方向的位移载荷来实现，其中压头作用在翘曲最高点位置，压头位移载荷（13.62 mm）、垫铁位置 (–152.5, 0, 10.97)、(152.5, 0, 10.8)）均按照表3和4理论计算的结果来进行设置，翘曲板材初始不平度大约为17.5 mm·m–1.

图12为上压头压下翘曲板材的矫直过程，图12(a)为压头将要与板材接触，图12(b)为压头下压到最低点的状态，铝板在压头位置受力最大，达到了55 MPa左右，图12(c)为压头上移到与板材分离的卸载过程，板材同时发生弹性回复，但反弯变形程度不均匀，在板材内部形成残余应力，局部位置点达到了25 MPa左右.

图12 压平矫直的有限元模型. (a)压平前; (b)压下最低点; (c)压平后Fig.12 Finite element model of flattening: (a) before flattening;(b) lowest position; (c) after flattening

在不同压下位移时，翘曲板材的残余挠度曲线如图13所示，横坐标为两个支点间的距离，3条曲线分别对应于与图12的板材横截面翘曲曲线分布，其中蓝色三角形的曲线形状为“M”型，表明在压头离开变形体，压头与板材接触部分发生了一定程度的局部变形，原因主要是由于实验用板材较薄，抗弯截面模量小，相同弯矩下弯曲应力更大，容易达到局部塑性状态. 仿真结果表明，以平均高度作为残余挠度，计算得最终变形体的残余挠度为1.21 mm·m–1、高度小于1 mm，这与现有仿真计算结果[6, 12]大小相当. 图14为压平过程压头受到的支反力大小，其在压下最低点支反力最大，达到了5863 N，在板材反弯段的压力平均值大约在4850 N，与考虑材料强化的理论计算结果偏差大约5.4%，表明理论模型具有可信性.

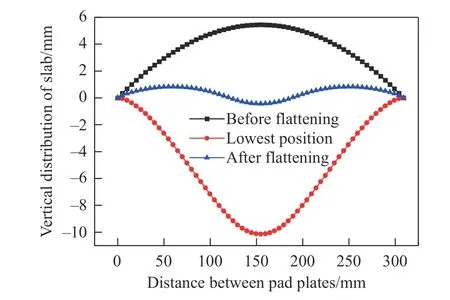
图13 压平过程有限元模型挠度曲线图Fig.13 Deflection curve of the finite element model in the flattening process

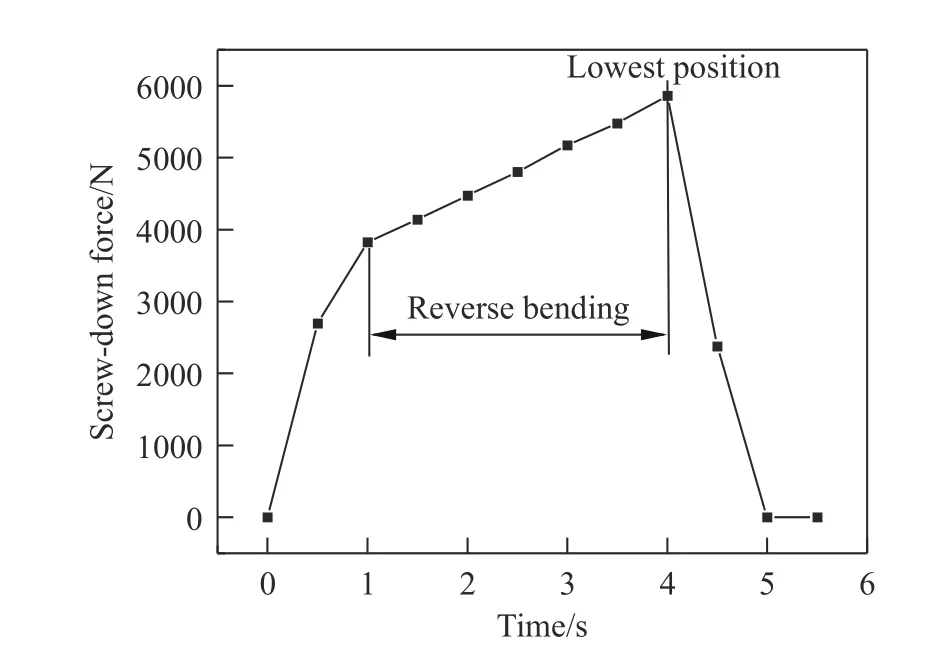
图14 模拟压下力Fig.14 Simulated screw-down force

为进一步验证基于点云数据计算的翘曲面压平工艺参数的合理性和准确性，利用液压机来进行三点弯曲压平实验，主要实验设备见图15. 将翘曲板材放置到承载平台上，按照表3计算的支点位置放置下垫铁块，在翘曲最高位置处放置上垫铁块，在液压压头与上垫铁块中间位置处加装压力传感器，进行压力测量.

图15 压平实验设备Fig.15 Experimental equipment of flattening

实验前两垫铁布置大致平行，支点距为305 mm，按照强化模型计算的压下位移载荷为13.62 mm，反弯挠度8.29 mm，实验时通过控制压机下压位移，并使用记号笔在立柱侧进行了标记，最终实际压下位移大约13.5 mm，实际反弯挠度大约8.25 mm.压平前后的金属板如图16所示. 压平前垫铁支点1和2位置对应的板材上表面高度h1和h2大约分别为10.8和10.9 mm, 最高点3对应的板材上表面高度h3大约16.5 mm, 进而可得两支点中间对应的初始挠度为5.25 mm，初始不平度大约17.2 mm·m–1，与基于机器视觉重构的三维曲面优化计算的参数差异不大. 卸载后，翘曲板材完成弹性恢复，最终铝板近似平直，高低点偏差大约1 mm，平直度从初始的大约17.2 mm·m–1减小到3.28 mm·m–1，满足GB/T—3880.3—2012要求的5 mm厚的一般冷轧板材不平度小于等于6 mm·m–1的要求，同时与现有报道的残余挠度1 mm结果相当[12]. 压平过程测量压下力如图17所示，从压平开始到压下最低点历时大约1.5 s，平均压下力大约5000 N左右，理论计算值(5110.5 N)与实测值的偏差大约为2.21%，有限元模拟结果(4850 N)与实测值偏差大约3%.通过对比可知，基于重构的翘曲板材三维曲面优化得到的两支点、压下位置点以及计算的翘曲曲率等数据进一步理论计算的压下位移、压下力与仿真和实验结果吻合度良好，压平矫直后板材平直，说明基于结构光视觉重构板材翘曲面的方法是可行的，相关模型是合理的.

图16 压平前后的翘曲板材Fig.16 Warped plate profile before and after flattening

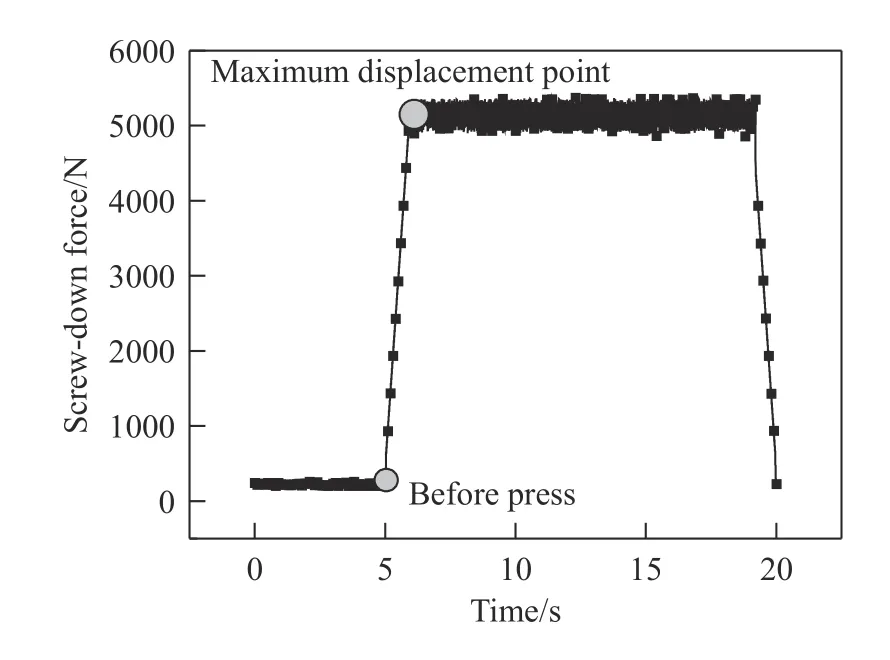
图17 实测压下力Fig.17 Measured screw-down force

5 结论

针对中厚板压平过程人工干预多、作业效率低、压平质量差的问题，采用了结构光相机实现了对翘曲板坯曲面的识别和三维重构，并建立了基于三维模型的压平参数计算模型，为精整压平智能化控制奠定了理论基础.

(1) 采用结构光相机对翘曲的铝板进行扫描可获得精度较高的表面点云，建立了结果准确、可靠的翘曲板面点云处理方法为翘曲板材曲面重构提供了技术路径.

(2) 基于最小二乘法建立了翘曲板材三维曲面拟合方法，拟合精度较高，可以应于板材翘曲面三维重构.

(3) 在重构的三维曲面方程的基础上，采用微分几何学的曲面论和三点弯曲矫平理论建立了翘曲板材压平工艺计算模型，并采用有限元方法进行了验证. 压平实验显示，理论计算压下力与实测偏差2.21%，按照理论计算方法工艺参数进行压平，压平后的板材平直度为3.28 mm·m–1，模型具有可靠性，可以为中厚板智能化控制提供基础支撑.