底吹氩钢包内废钢熔化行为的数值模拟

张利超，方 庆，周文浩，王家辉，余 刚，张 华，倪红卫

1) 武汉科技大学钢铁冶金及资源利用省部共建教育部重点实验室，武汉 430081 2) 湖南华菱湘潭钢铁有限公司，湘潭 411101

炼钢过程中，铁矿石和废钢是生产程序的主要原料，其中废钢相比较于铁矿石有减小能耗，可再生资源、节能环保等特点，较多的使用废钢还可以有效的减小矿产资源的消耗，因此如何提高废钢在炼钢中的占比成为了国内外学者广泛关注的重点[1-3]. 目前，关于废钢在冶炼熔池内熔化机理已有较多的研究[4-12]. Gao等[4-5]分析了自然对流条件下废钢的二维换热过程，实现了废钢温度分布的可视化. Xi等[6-7]使用多棒材钢样在钢液中熔化特征基础上，建立了废钢熔化数学模型，由此预测废钢在电弧炉中的熔化时间. Deng等[8-9]为了进一步提高铁水包中的废钢配比，通过Fluent软件对废钢熔化进行研究，得到不同废钢比下的熔化时间. 但上述研究多限定在实验室内特定环境下，即使给定对流条件，与实际生产炉内流动氛围不相符，研究结果对生产指导意义有限. 同时，关于废钢熔化的数值模拟研究多为二维模型，只针对实验条件进行对比验证，未考虑废钢在实际生产环境下的熔化行为.

“双碳”背景下，众多生铁产量受限，转炉吃废钢能力有限，为提升废钢利用率，开发多点加废钢技术应运而生. 多点加废钢指的是在转炉炼钢生产的各个阶段加入适量和合适的废钢，最大限度地节能减排，降低生产成本，在钢铁企业中，往往钢包加废钢技术也是其重要一环，并逐渐受到国内外冶金专家的重视. 钢包加废钢熔化的特点是氩气改变钢包内的流场对废钢熔化行为产生影响且降低废钢加入对钢液洁净度和成分的影响，一般而言，钢包内加入废钢成分应与钢水成分差别不大. 祁政伟和雷佳奋[13]总结出钢包内废钢的加入方式多通过破碎皮带运至料仓并采用溜管入包，废钢在溜管给予的初速度与重力的双重作用下浸入钢液中，大部分会沉到钢包底部. 王飞宇等[14]结合现场对废钢熔点和成分进行计算分析，得到LF精炼炉内应使用洁净的钢筋头作为入炉废钢，为钢包内加废钢的实现提供可能，并通过效益核算发现，当LF精炼使用的废钢价格与实际钢坯销售价格差值在280元·t–1以上时，可产生明显经济效益. 故对钢包加废钢熔化行为的研究无论是从可行性还是环境和成本方面考量均有重要意义.然而，目前鲜有关于底吹氩钢包内废钢熔化行为规律的三维数值模拟研究报道.

某厂70 t钢包采用专门的提升装置向每炉中加入20～30 kg·t–1的废钢，为探明废钢料在底吹氩钢包内的熔化行为规律，促进废钢的熔化和混合，本文建立三维耦合数学模型，研究不同形状（同体积）废钢、吹氩量及废钢预热温度对钢包内流场、温度场及废钢熔化行为的机制，为实际生产应用提供理论指导.

1 模型与方程

1.1 基本假设

钢包内部废钢的熔化本身是一个复杂的化学过程，不仅有钢液和废钢间的传热，还包括氩气对于钢液和废钢的影响. 为了方便研究废钢在钢包内的熔化过程，对模型做下列假设[15-17]：

（1）钢包壁面没有热量损失与环境没有热量交换，钢包上表面与钢包壁面相同处理；

（2）每个相之间不包含复杂的化学反应，钢液与废钢原始成分相同；

（3）钢包内的氩气入口速度恒定，温度与钢包内部相同；

（4）氩气泡直径固定为2 mm，忽略气泡间的相互作用力；

（5）忽略顶部渣层对于钢包流场和废钢熔化的影响.

1.2 控制方程

1.2.1 连续性方程

根据质量守恒原理，可得三维连续性方程如下[18]：

式中，ρ为钢水的密度，单位为kg·m–3；vi为不同方向上的速度，单位为m·s–1.

1.2.2 动量方程

通过动量守恒定律，得到下列动量方程[19]：

式中，µ为流体黏度，单位为kg·m–1·s–1；P是压力，单位为Pa；S为源项，用于将糊状区的速度逐渐减小为零；β为液相分数，ε是一个小的数字为0.001；Amush是糊状区参数，Hietanen等[20]研究了糊状区参数在103～107区间时对于钢液凝固的影响，得到107更符合实际情况，本文最终确定糊状区参数为107.

1.2.3 湍流方程

流动行为使用湍流方程进行表示，选用Realizablek–ε双方程模型，其中k和ε方程可由（4）和（5）来表示[21-22]：

式中，k和ε分别是湍动能和湍流耗散率；Gk为速度梯度所产生的湍流动能；Gb是由浮力所引起的湍流动能；σk和σε分别为k和ε的湍流普朗特数，µt为湍流黏度可由下式（6）表示：

式中，cµ为局部流动的涡流黏度系数；C1ε=1.44，C2=1.9，σk=1.0和σε=1.2为Realizablek–ε模型常数.

1.2.4 能量方程

由能量守恒原理得能量方程表达式如下[23-24]：

式中，H和h分别比焓和潜热焓，单位都为J·kg–1，下标ref表示为参考状态下；k和cp分别为导热率和比热容，单位为W·m–1·K–1和J·kg–1·K–1；L代表相变潜热，单位为J·kg–1.

1.2.5 凝固熔化模型

使用凝固熔化模型对废钢在钢包中的熔化过程进行模拟，其特点为引入“糊状区”参数对废钢在钢包内的凝固层进行定义，具体液相分数可由方程式（9）来表示[25-26]：

式中，Tsolidus和Tliquidus分别为固相线温度和液相线温度，T为某一时刻的温度，温度单位均为K.

1.2.6 Discrete Phase Model模型

采用DPM模型对钢包底吹氩过程进行模拟，将气泡视为离散相来实现气泡在钢包内的运动状态. 通过对气泡上所存在的力进行解析，得到钢包底吹氩气过程氩气泡的运动轨迹，作用力方程（10）[27-28]：

式中，µ为流体分子的黏度，单位为Pa·s；dp是氩气泡直径，单位为m，气泡形状固定为球形；CD为摇曳系数；Re为相对雷诺数；是单位气泡在所受的其他力，其中包括虚拟质量力和压力梯度力可由式（12）和（13）表示[29]：

式中，CVM为虚拟质量因子，其值为0.5；∇→u为对→u的算符矢量，即对分量的偏导.

1.3 网格及参数

本文以某厂70 t钢包为研究对象，图1为钢包底吹氩模型图，为确保计算精度同时提高计算速度，将废钢以及周围网格进行加密. 表1为该厂钢包炉的尺寸及主要工艺参数，其中透气砖位置中的R表示为钢包底部半径，0.5R为距钢包底部中心的距离为R的一半，本文使用ANSYS FLUENT软件对钢包内底吹氩气时的钢液流动和废钢熔化过程进行数值模拟.

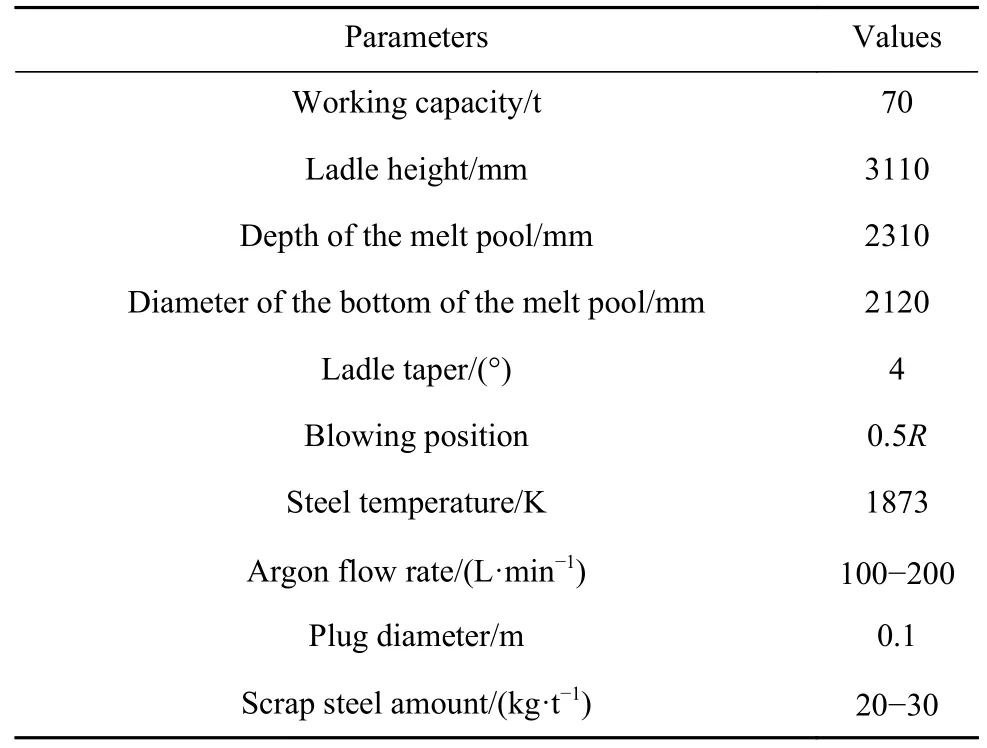
表1 钢包炉基本尺寸及主要工艺参数Table 1 Basic dimensions of the ladle and its main industrial parameters

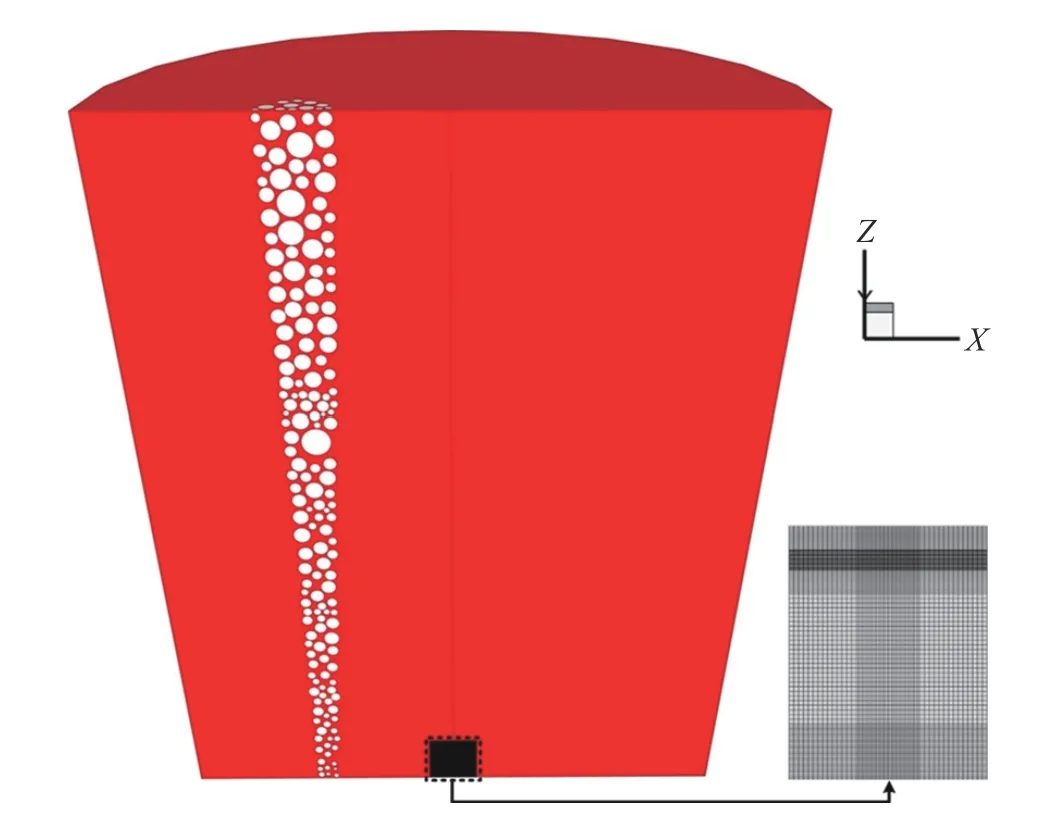
图1 钢包中废钢及周围网格示意图Fig.1 Scrap steel in the ladle and its diagram of the surrounding grid

表2为钢包内钢液与废钢的物理性质，依据溶池钢水和所用废钢化学成分，其中，密度、导热率、比热容和黏度的值为随温度变化的函数（图2）.

表2 模拟过程使用的物理性质Table 2 Physical properties used in the simulation process

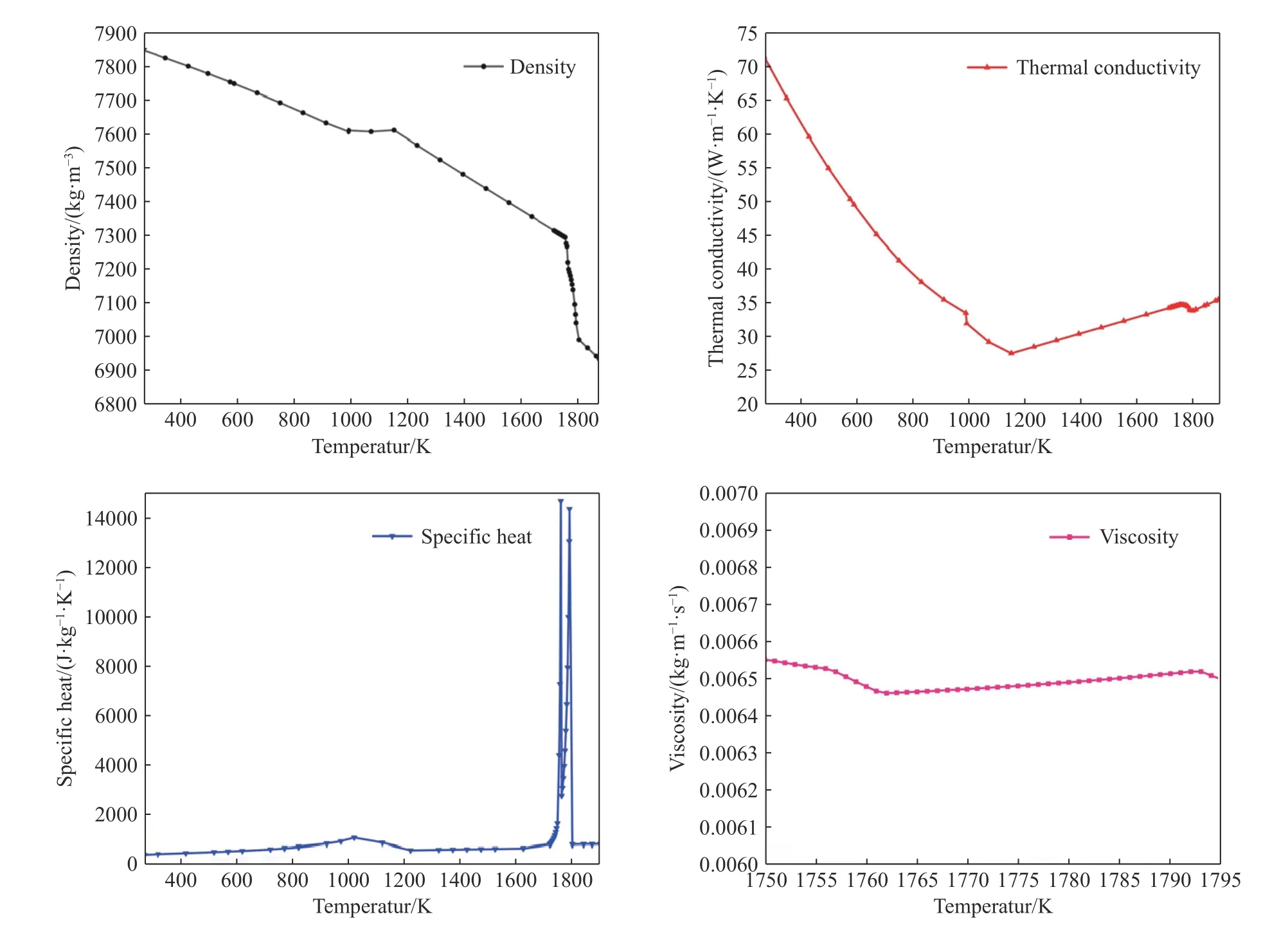
图2 钢液热物性参数与温度的关系. （a）密度；（b）导热率；（c）比热容；（d）黏度Fig.2 Variations of thermophysical parameters of steel with temperature: (a) density; (b) thermal conductivity; (c) specific heat; (d) viscosity

1.4 研究方案

钢包内底部吹气元件（0.5R）和废钢（中心）位置，探究废钢在预热温度为800 K时钢包内不同形状的废钢熔化，得到相同体积下不同比表面积的圆柱形、方形、板形废钢熔化规律，再对板形废钢的四种（300、500、800和1000 K）不同预热温度进行研究，最后对钢包内三种不同底吹氩气流量（100、150和200 L·min–1）下的废钢周围流场进行比较分析，得到废钢熔化规律性研究. 表3为三种废钢的尺寸、比表面积大小.

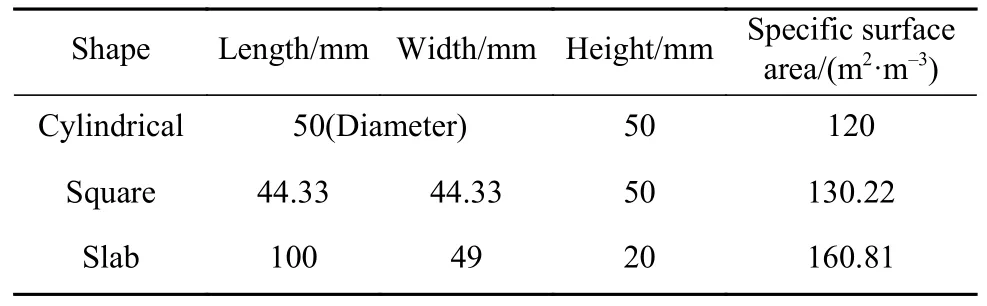
表3 不同比表面积废钢尺寸分布Table 3 Scrap size distribution with different specific surface areas

1.5 钢包的边界条件及求解方法

钢包整体分为上表面，钢包壁面，下表面和入口处，使用DPM模型模拟底吹氩气，整个空间处于密闭状态，壁面使用无滑移边界条件，采取标准壁面函数处理，钢包内底吹氩气在入口和出口处的边界条件为escape.

氩气进入钢液的速度大小是由单位时间内通过底部透气砖的氩气体积所决定的，钢包内底吹氩气入口处的湍动能Kin及湍流耗散率ε由式（14）表示[30-31]：

式中，Vm为氩气流入钢液的速度大小；Dping为底部透气砖面积大小.

钢包内废钢的整个熔化过程与时间息息相关，所以采用基于压力求解器的非稳态求解方法，即压力修正法，其求解算法有SIMPLE、SIMPLEC和PISO!本文选用PISO!算法，压力离散方式为PRESTO!.动量、湍动能、湍流耗散率和能量的离散方式均选用二阶迎风格式，除能量方程的收敛标准为10–6，其余各求解方程的收敛标准均为10–3.

2 模型验证

Xi等[17]使用圆棒形状的GCr15轴承钢，在同种钢液类型下，采用中频感应炉进行了钢筋熔化热态模拟实验. 为验证本模型的准确性，本文建立与文献[17]中图2的熔化实验参数一致的数学模型计算直径15 mm、长200 mm和浸没深度为180 mm的废钢在钢液内熔化行为，数值模拟得到的废钢形貌随时间变化如图3所示. 结合文献[17]中图2和本文相同条件下的数值模拟结果可知，圆形废钢棒在浸入到钢液时会产生凝钢层，在10 s左右时凝钢层达到最大，之后凝钢层逐渐消失，废钢开始熔化，直到废钢在70 s左右断裂. 数值模拟得到的废钢熔化行为和形貌与同等条件下的废钢熔化实验结果基本吻合.

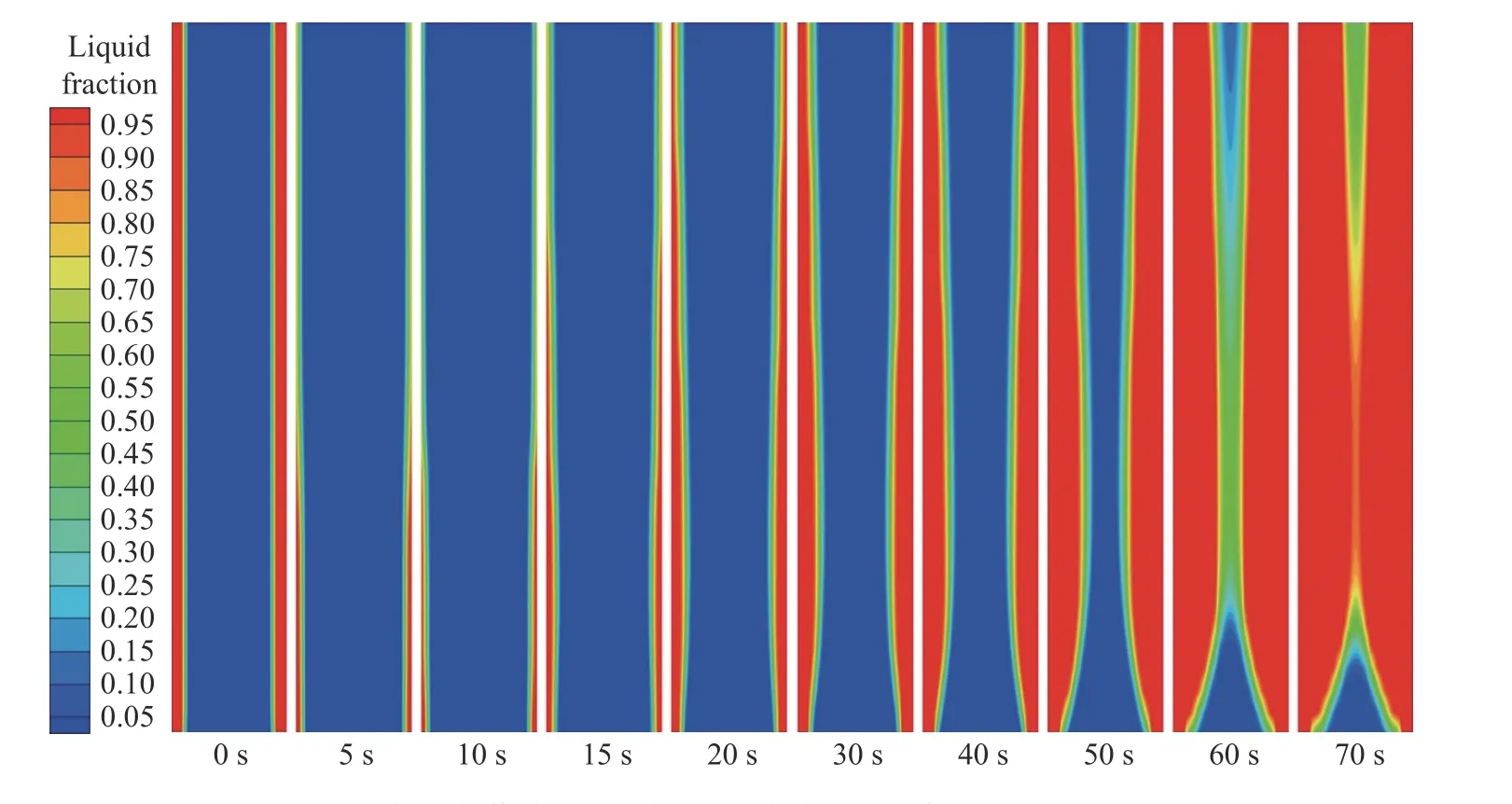
图3 数值模拟下钢棒在钢液内熔化时形貌随时间变化Fig.3 Numerical results of steel bar morphologies during the melting process at different time

3 结果分析与讨论

3.1 钢包内不同形状废钢的熔化行为

废钢形状（比表面积）是影响熔化速度的关键因素，针对钢包加废钢熔化过程，对比分析预热温度为800 K时同体积（质量），形状分别为圆柱形、方形和板形的废钢在有无底吹氩钢包内的熔化行为，探讨底吹工艺和比表面积对废钢熔化速度的影响机制.

3.1.1 有无底吹氩对废钢温度的影响

图4为有无底吹氩气下Z=10 mm截面内板形废钢温度场随时间的变化. 由图4可知，10 s左右时废钢大部分区域温度仍在1700 K以下，20 s后大部分区域温度已经达到1740 K以上，只有无底吹条件下的废钢中心小部分区域温度在1730 K以下，直到30 s时底吹氩气流量为200 L·min–1的废钢区域温度已经达到1770 K以上，而无底吹的废钢仍有部分区域在1760 K以下，这主要是由于氩气的增加，促使钢液熔池内存在强烈的搅拌形成强制对流，加速了废钢与钢液间温度的传递. 即钢包有底吹氩气时废钢区域的温度明显比无底吹氩气温度变化更快.

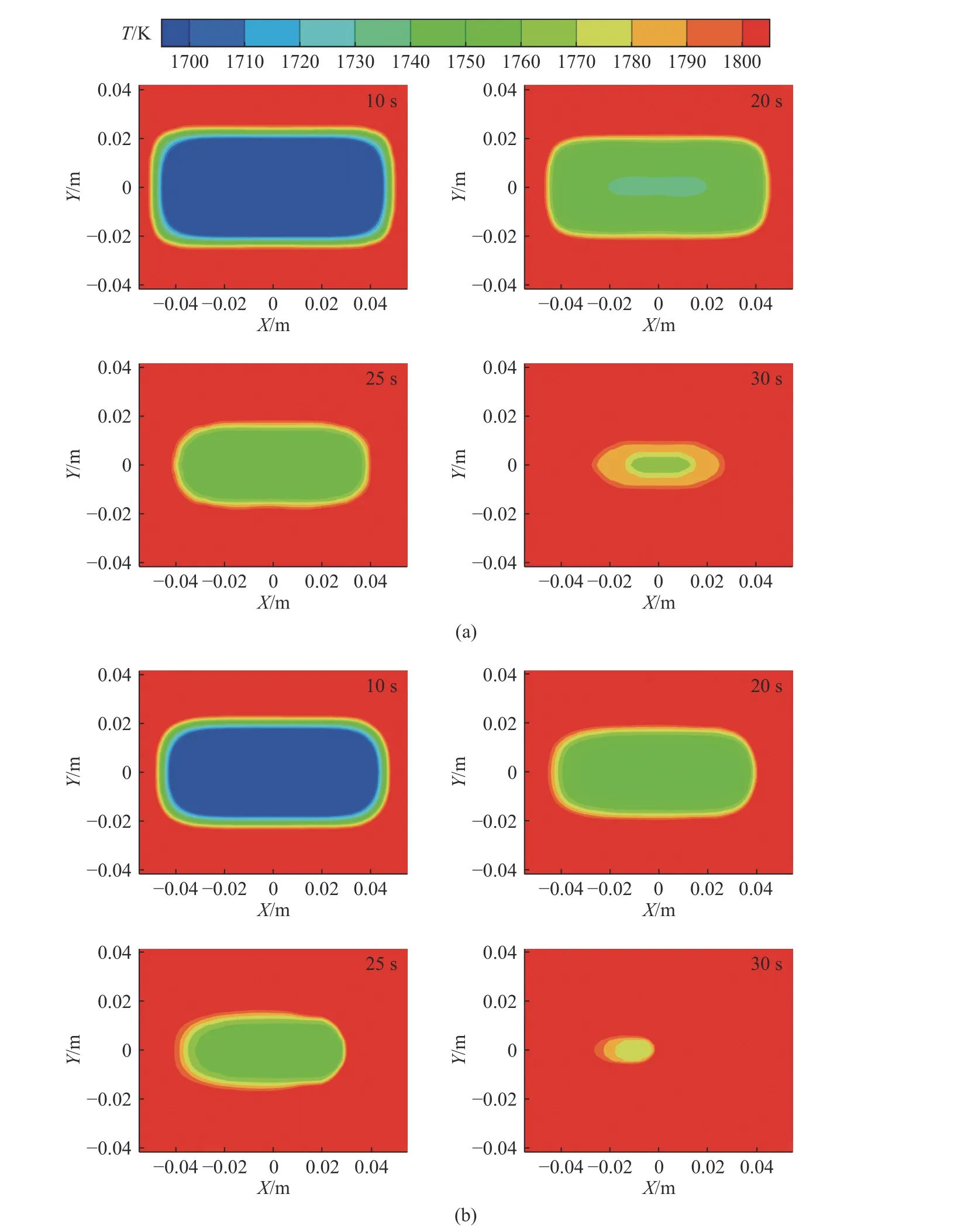
图4 有无底吹氩气钢包中板形废钢温度随时间变化. （a）无底吹；（b）200 L·min–1Fig.4 Temperature variations of slab scrap in the ladle with and without argon blowing at different time: (a) without bottom blowing; (b) 200 L·min–1

图5为有无底吹氩钢包内不同形状废钢中心温度随时间变化关系，其中TL和TS分别为液相线温度和固相线温度. 从图5可以看出，废钢中心温度与熔化时间成线性关系，这与前人的热模拟实验结果较为吻合[17]. 无底吹氩气时，圆柱形、方形和板形废钢的中心温度到达固相线温度的所需时间分别为42、41和26 s，中心温度的升温速率分别为22.61、23.17和36.53 K·s–1；有底吹氩气时，圆柱形、方形和板形废钢的中心温度到达固相线温度的升温速率分别为29.67、29.67和41.3 K·s–1. 有底吹氩条件下圆柱形废钢相比较无底吹条件下废钢熔化时间缩短了10 s，中心温度的上升速率提高了7.06 K·s–1，当废钢为方形和板形时，中心温度上升速率分别提高了6.51和3.73 K·s–1.

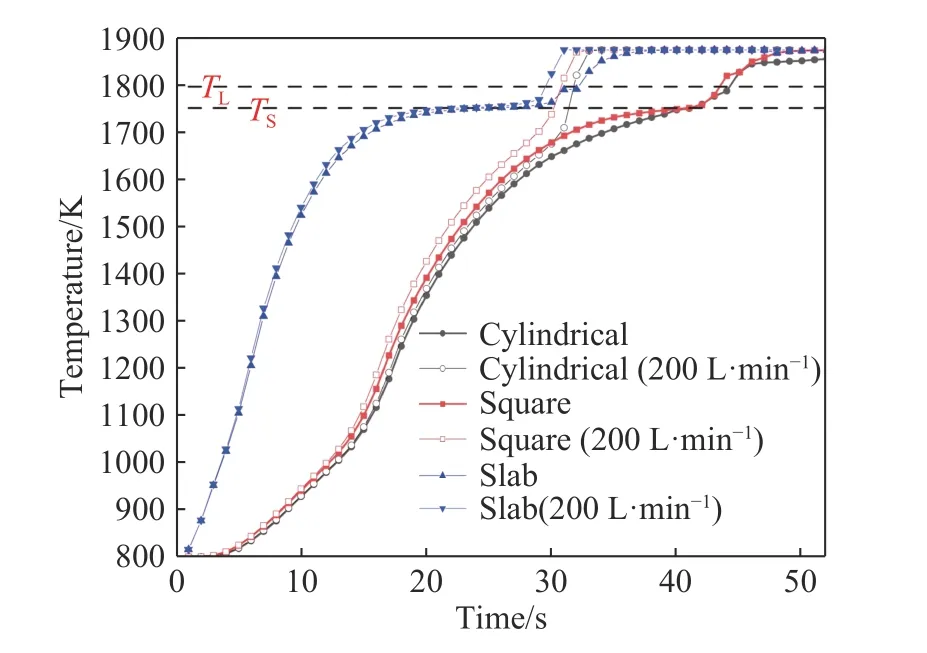
图5 有无底吹氩钢包内不同形状废钢中心温度随时间变化关系Fig.5 Variations of central temperature with different shapes of scrap during the melting process in the ladle with and without argon blowing as a function of time

3.1.2 有无底吹氩对废钢熔化行为的影响

图6为有无底吹氩钢包内板形废钢的熔化过程. 由图6可知，在废钢开始熔化的初始阶段（10 s之前）有无底吹氩气钢包内废钢形貌变化无明显区别，10 s时，两种情况板形废钢的角部位置均已完全熔化. 20 s时，有底吹氩气下的板形废钢形貌要明显小于无底吹氩气下的废钢形貌，熔化时间为30 s时，有底吹氩的废钢剩余体积仅为3.26 cm3，而无底吹氩的废钢剩余体积为15.68 cm3要明显更大一些. 这主要是因为当透气砖内有氩气进入钢液时，让钢液产生一定的流动，进而加速废钢的熔化，使得有底吹氩气比无底吹氩气的废钢熔化更快.

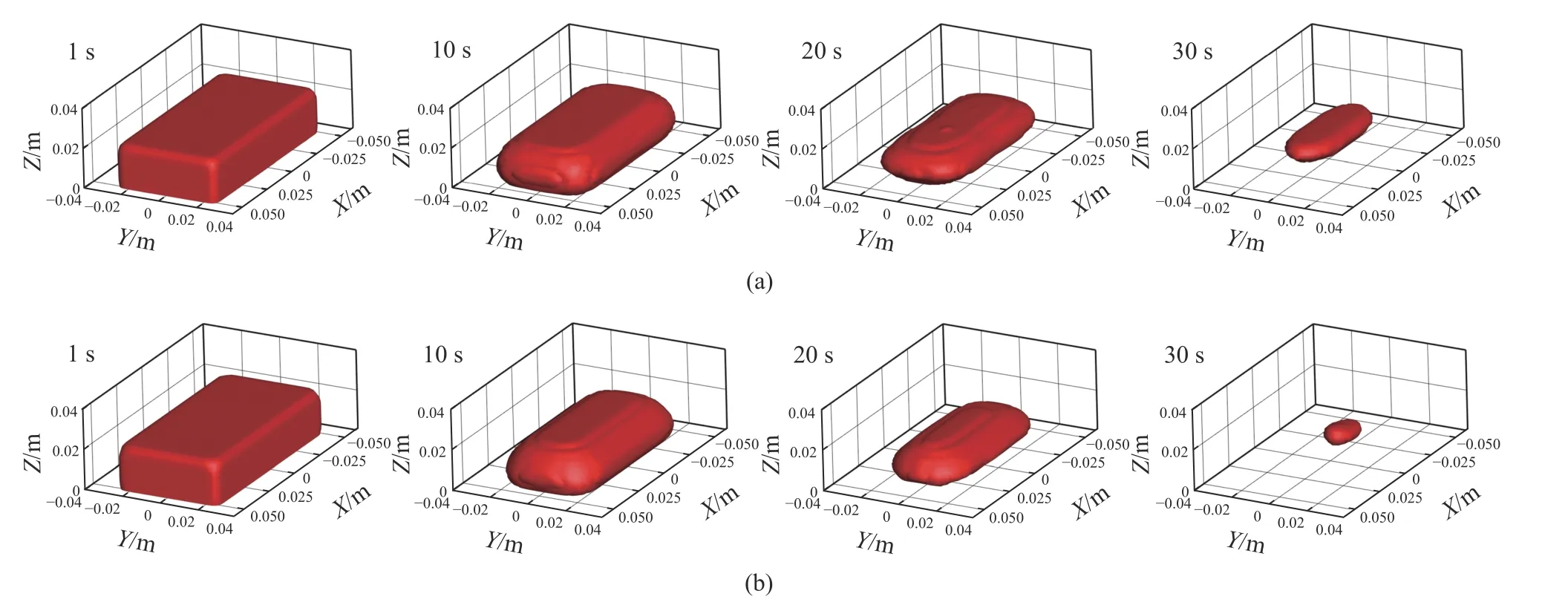
图6 有无底吹氩气钢包内板形废钢熔化现象. （a）无底吹；（b）200 L·min–1Fig.6 Melting of slab scrap in the ladle with and without bottom argon blowing: (a) without bottom blowing; (b) 200 L·min–1

图7为有无底吹氩钢包内不同形状废钢的剩余体积随时间变化关系. 其中无底吹氩钢包内圆柱形、方形和板形废钢完全熔化时间分别为52、49和34 s，熔化速率分别为1.88、2和2.88 cm3·s–1，底吹氩气流量为200 L·min–1下圆柱形、方形和板形废钢完全熔化时间分别为35、34和31 s，熔化速率分别为2.8、2.88和3.16 cm3·s–1，相比较无底吹氩气而言，有底吹氩气时圆柱形、方形和板形废钢的完全熔化时间分别减小了17、15和3 s，熔化速率分别提高了0.92、0.88和0.28 cm3·s–1. 当底吹氩流量由0增至200 L·min–1时，比表面积较小的圆柱形废钢熔化速率提高了0.92 cm3·s–1，而比表面积较大的板形废钢熔化速率只提高了0.28 cm3·s–1，由此可得，钢包内随着废钢比表面积的增大，底吹氩气对废钢熔化速度的影响效果在逐渐减缓. 底吹氩气对钢包内废钢熔化行为有明显的促进效果，同时当废钢比表面积较小时，底吹氩气对其熔化影响较大，但随着废钢比表面积的增大，底吹氩气对废钢熔化的影响在逐渐减缓.

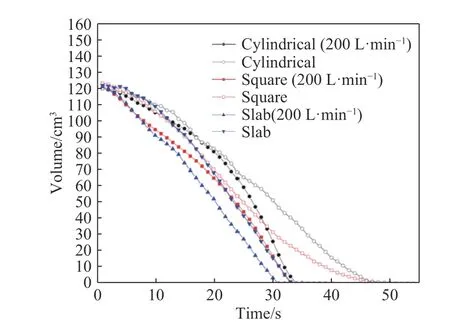
图7 有无底吹氩钢包内不同形状废钢体积随时间变化关系Fig.7 Volume of scrap with different shapes in the ladle with and without argon blowing a function of time

3.2 钢包内预热温度对废钢熔化的影响

废钢的预热温度是影响熔化速度的关键因素，针对钢包加废钢熔化过程，对比分析底吹氩流量200 L·min–1时，预热温度分别为500、800和1000 K下底吹氩钢包内废钢的熔化行为，探讨预热温度对废钢熔化速度的影响机制.

3.2.1 不同预热温度对废钢温度的影响

图8 为底吹氩钢包内不同预热温度下Z=10 mm截面内板形废钢温度云图随时间变化关系. 由图8可知，10 s左右时，不同预热温度下废钢大部分区域的温度在1700 K以下，20 s后废钢大部分区域的温度达到1740 K以上，中心区域的温度在1720 K左右，当预热温度为1000 K时，废钢区域的温度在30 s已全部达到1800 K以上，而预热温度为300、500和800 K时仍有部分区域温度在1780 K以下.同时，在相同时刻下预热温度越高废钢整体温度变化越快. 图8为钢包内不同预热温度下板形废钢中心温度随时间变化曲线. 由图9可知，当废钢预热温度为1000 K时，中心温度到达固相线温度所需时间为22 s，相较于预热温度分别为300、500和800 K时，所需时间分别仅减少了3、2和1 s，这主要是由于预热温度的提高，导致钢液与废钢之间的温度梯度降低，即钢液与废钢的热量交换时间有所缩短，也就是预热温度越高废钢中心温度上升到固相线温度所需时间越短.

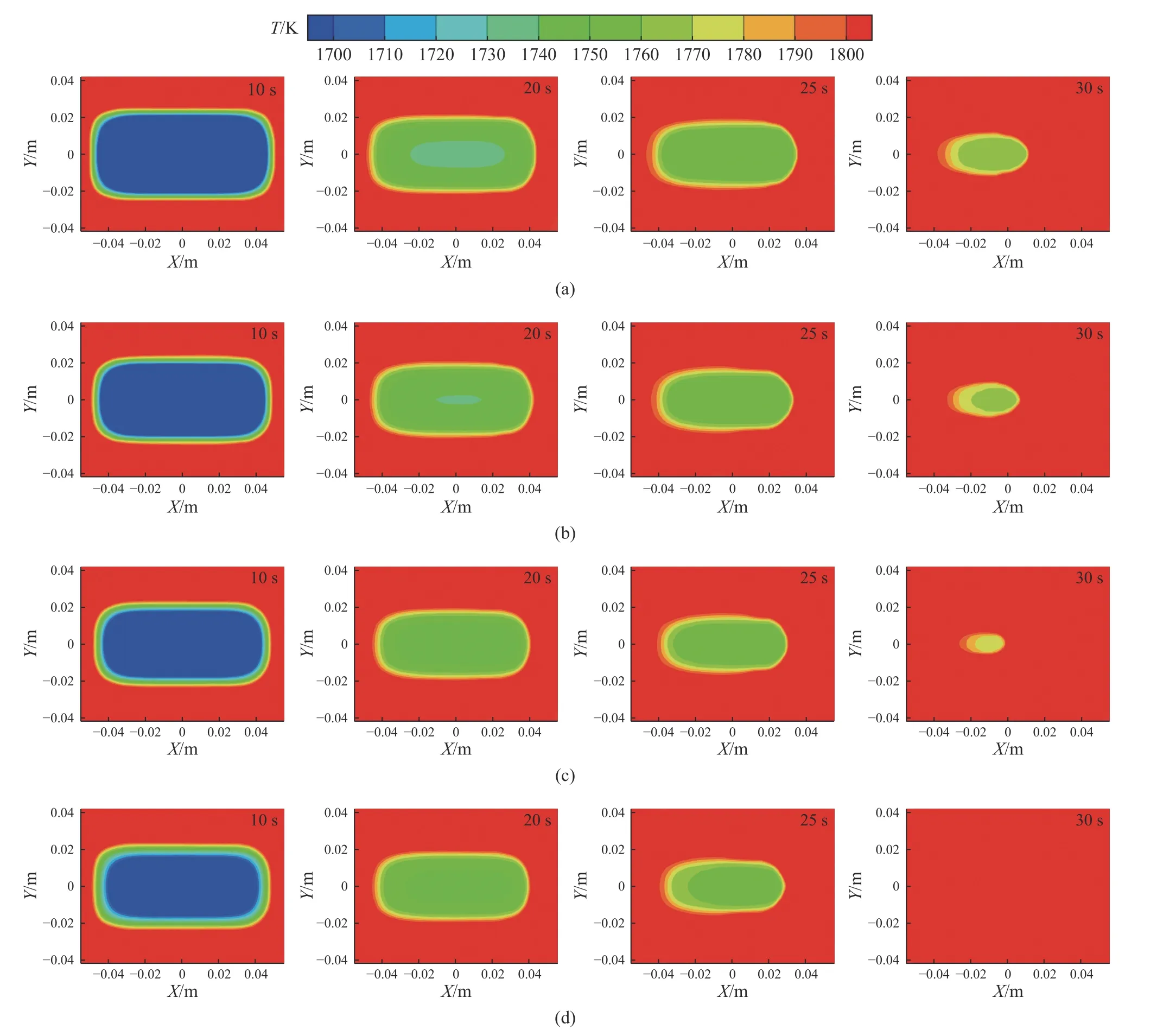
图8 钢包内不同预热温度下板形废钢温度随时间变化. （a）300 K;（b）500 K;（c）800 K；（d）1000 KFig.8 Temperature variation of slab scrap with time at different preheating temperatures in the ladle: (a) 300 K; (b) 500 K; (c) 800 K; (d)1000 K

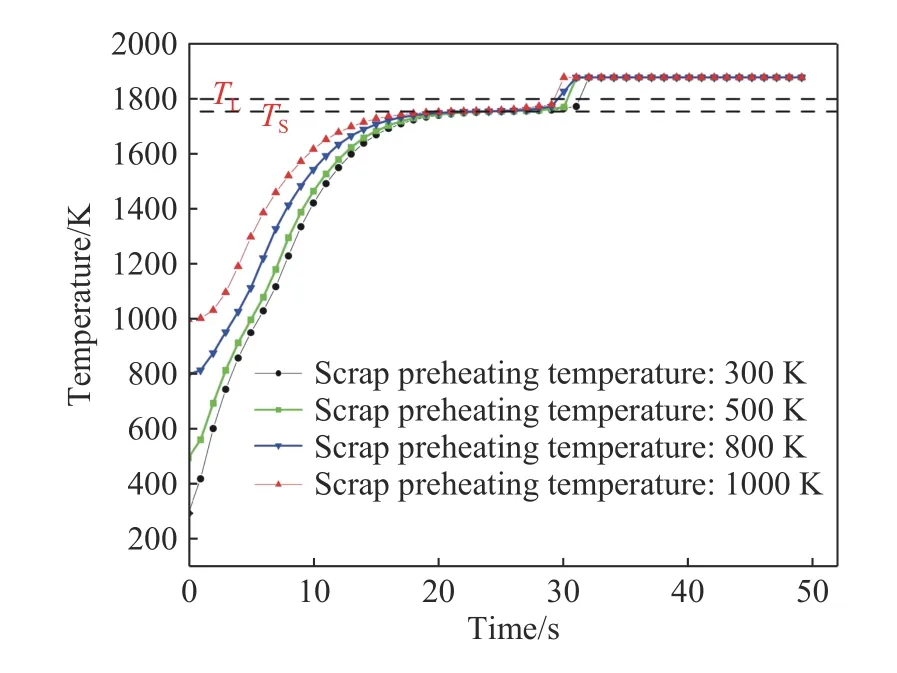
图9 钢包内不同预热温度下板形废钢的中心温度随时间变化关系Fig.9 Change in center temperature of slab scrap with time under different preheating temperatures in the ladle

3.2.2 不同预热温度对废钢熔化行为的影响

图10为钢包内不同预热温度下板形废钢的熔化现象. 由图10可知，在废钢开始熔化的初始阶段（10 s之前）底吹氩钢包内不同预热温度废钢的形貌变化无明显区别，10 s时，两种情况下板形废钢的角部位置均已完全熔化. 20 s时，预热温度为800 K的板形废钢体积要明显小于预热温度为300 K的废钢体积，30 s时，预热温度为800 K的废钢剩余体积仅为3.26 cm3，而预热温度为300 K的废钢剩余体积为11.47 cm3. 说明提高预热温度对板形废钢熔化前期（20 s之前）形貌变化影响不大，在20 s之后不同预热温度下的板形废钢形貌的大小才明显有所区别.

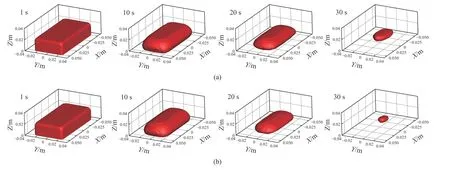
图10 钢包内不同预热温度下板形废钢的熔化现象. （a）300 K；（b）800 KFig.10 Melting phenomenon of sheet scrap at different preheating temperatures in the ladle: （a）300 K；（b）800 K

图11为钢包内不同预热温度下板形废钢的体积随时间变化曲线. 在图中相同时刻下预热温度越高，废钢的剩余体积越小，其中预热温度分别为300、500、800和1000 K的板形废钢完全熔化时间分别为33、32、31和30 s，熔化速率分别为2.97、3.06、3.16和3.26 cm3·s–1，即废钢初始温度每上升100 K，其熔化速度约提高0.058 cm3·s–1. 说明提高预热温度在20 s之前对废钢的熔化过程形貌变化影响虽然不大，但对其熔化速率确实存在一定程度的影响.

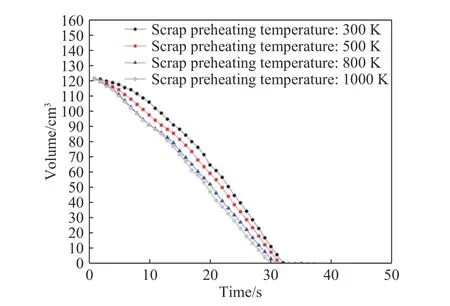
图11 钢包内不同预热温度下板形废钢的体积随时间变化Fig.11 Volume of sheet scrap in the ladle varies with time at different preheating temperatures

3.3 钢包内底吹氩气流量对废钢熔化的影响

不同底吹氩气流量是研究钢包内流场的前提，也是影响钢包内废钢熔化过程的重要条件，本节对比分析废钢预热温度为800 K时，底吹氩气流量分别为100、150和200 L·min–1下的废钢熔化规律.

3.3.1 不同底吹氩气流量对废钢周围流场的影响

图12 为不同底吹氩气流量下Y=0 mm截面内板形废钢周围的速度云图. 由图可知，无底吹氩气时，钢包内钢液的流速是在0.01 m·s–1以下，只有废钢周围的大部分钢液流速在0.01 m·s–1左右，少部分区域速度达到0.02 m·s–1. 流量为100 L·min–1时，板形废钢周围钢液大部分区域的流速在0.015 m·s–1以上，且废钢远离透气砖侧的钢液产生了一处环流，之后随着流量的增大，环流消失，流量为150 L·min–1时，板形废钢周围钢液大部分区域流速在0.035 m·s–1以上，流量为200 L·min–1时，废钢周围大部分区域流速在0.05 m·s–1以上. 结合图中废钢周围钢液的速度大小和迹线分布，可以看出，钢包内废钢熔化速度的提升，主要是由于随着底吹氩气流量的增大，气流对熔池搅拌强度增强，加速了钢液与废钢表面的对流换热，从而促使废钢快速熔化. 图中迹线的箭头方向代表了钢包内部钢液流动的方向，可以看出远离透气砖侧的废钢受到钢液的冲刷较为严重，所以远离透气砖侧的废钢熔化较为明显.

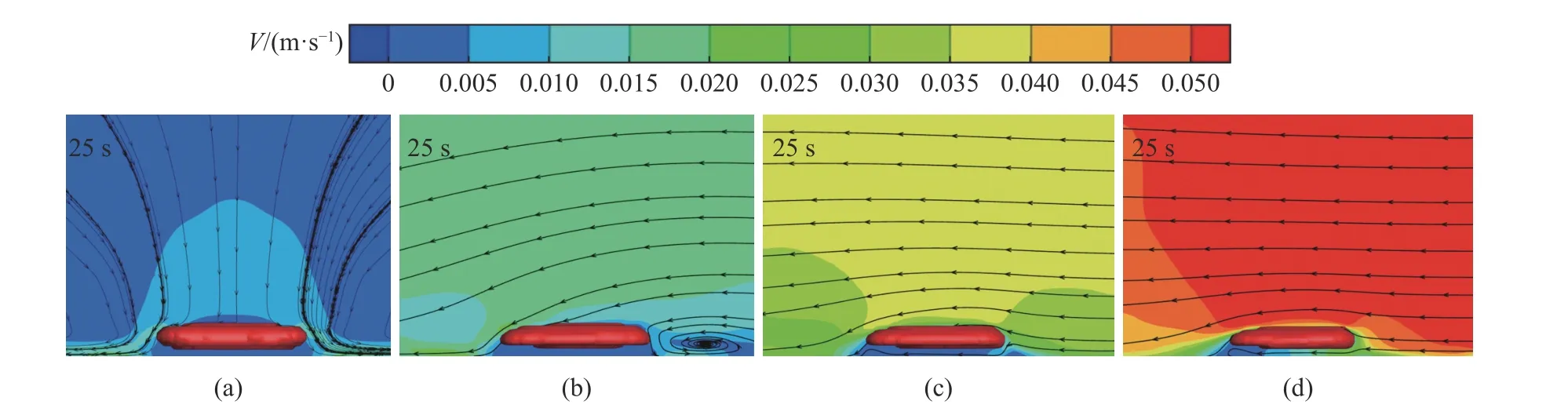
图12 不同底吹氩气流量下钢包内板形废钢周围速度云图. （a）无底吹；（b）100 L·min–1；（c）150 L·min–1；（d）200 L·min–1Fig.12 Velocity cloud diagrams around the slab scrap in the ladle with and without argon blowing: (a) without bottom blowing; (b) 100 L·min–1;(c) 150 L·min–1; (d) 200 L·min–1

3.3.2 不同底吹氩气流量对废钢温度的影响

图13为不同底吹氩气流量下Z=10 mm截面内板形废钢温度场随时间变化关系. 从图中可以看出，20 s之前，不同底吹流量下废钢的温度变化相差不大，20 s时废钢整体温度在1740 K以上. 30 s时，底吹流量为200 L·min–1的废钢区域大部分温度达到1800 K以上，仅有中心少部分区域的温度在1770～1780 K，此时、废钢低于1780 K区域的面积要明显小于100 L·min–1和200 L·min–1流量下的废钢面积. 图14为不同底吹氩气流量下钢包内板形废钢中心温度随时间变化关系. 由图可知，在底吹氩气流量为100、150和200 L·min–1时，废钢中心温度到达固相线温度所需时间分别为24、23和22 s，中心温度上升速率分别为44.7，46.65和48.77 K·s–1. 从3.3.1节可知，造成中心温度上升速率改变的原因主要是废钢周围速度的加快，促使钢液流动，加快废钢与钢液间的温度传递，所以同一时刻下流量越大，废钢中心温度上升越快.

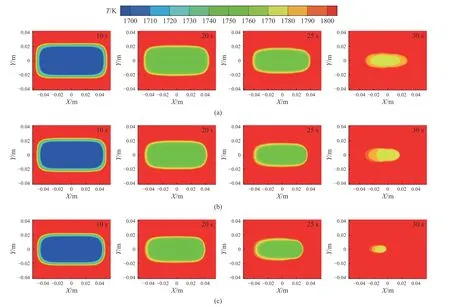
图13 不同底吹氩气流量下钢包内板形废钢熔化过程温度变化. （a）100 L·min–1；（b）150 L·min–1；（c）200 L·min–1Fig.13 Temperature variation of slab scrap in the bottom argon ladle during the melting process at different flow rates: (a) 100 L·min–1; (b) 150 L·min–1;(c) 200 L·min–1

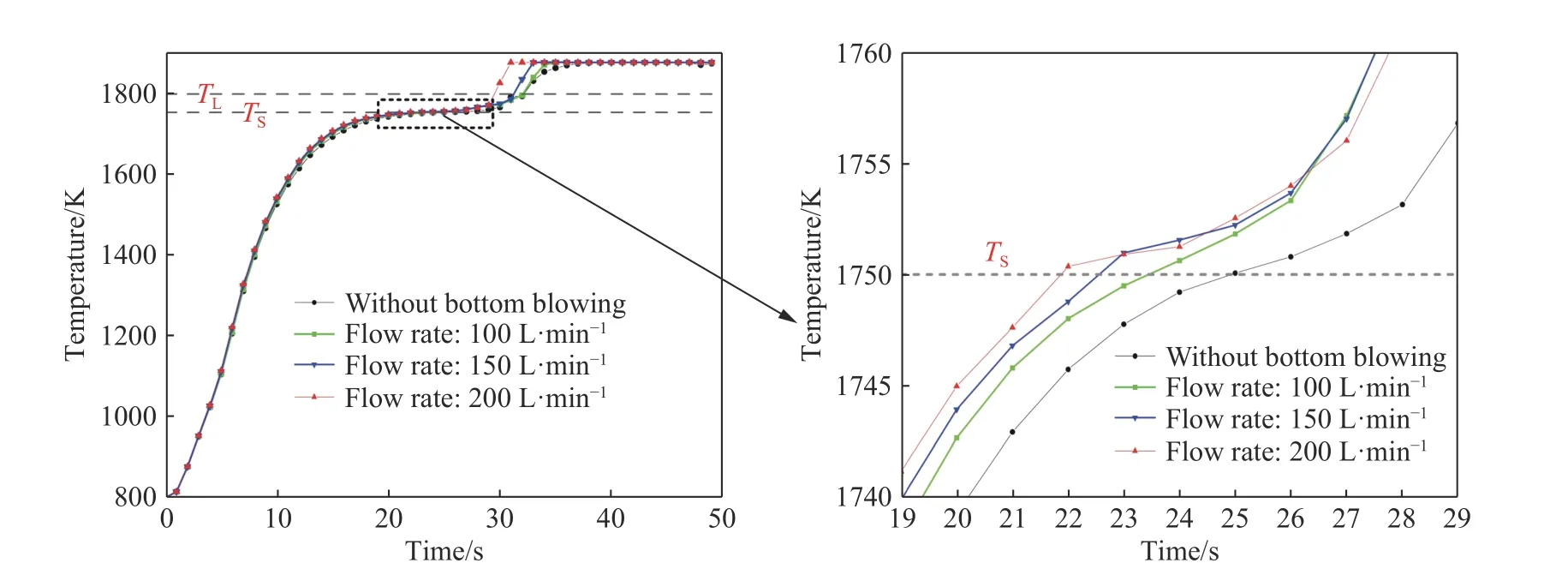
图14 不同底吹氩气流量下钢包内板形废钢中心温度随时间变化关系Fig.14 Temperature variation with time in the center of plate-shaped scrap in ladle under different bottom-blowing argon flow rates

3.3.3 不同底吹氩气流量对废钢熔化行为的影响

图15为不同底吹氩气流量下钢包内板形废钢的熔化现象. 由图15可知，在废钢开始熔化的初始阶段（10 s之前）不同底吹氩气流量下钢包内废钢的形貌变化无明显区别，10 s时，两种情况下板形废钢的角部位置均已完全熔化. 20 s时，流量为200 L·min–1钢包内的板形废钢形貌要明显小于另外两种流量下的废钢形貌；30 s时，流量为200 L·min–1的废钢剩余体积仅为3.26 cm3，而流量分别为150和100 L·min–1下的废钢剩余体积分别为10.47和13.36 cm3. 说明增加底吹氩气流量在废钢熔化10 s之前对废钢形貌熔化影响不大，之后形貌变化较为明显. 这是由于钢液流动速度与对流传热系数息息相关，从上述看出底吹氩气流量增大，废钢周围钢液流速加快，相应的对流传热系数增大，从而促使钢液向废钢传热，加快废钢的形貌变化.

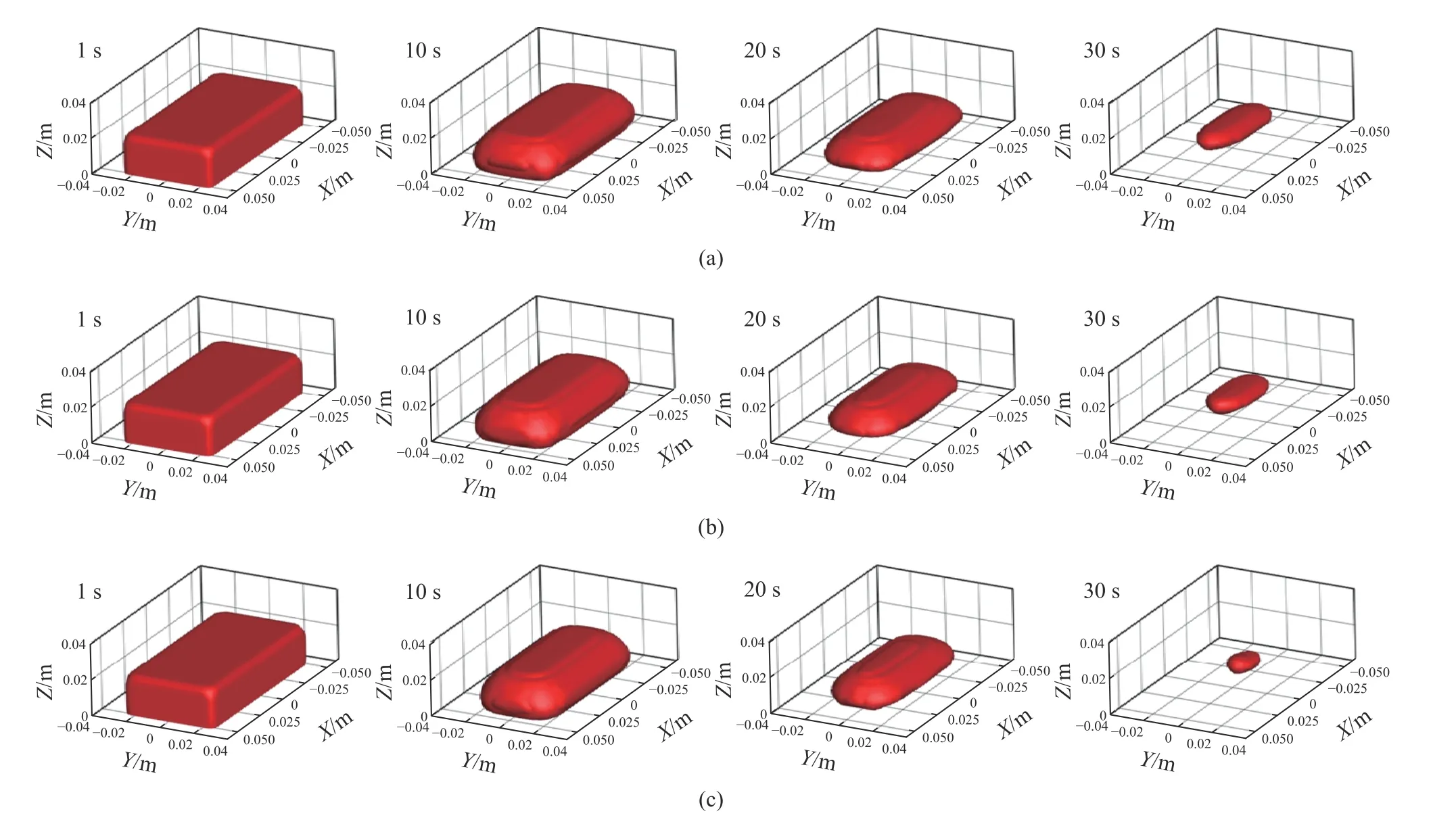
图15 不同底吹氩气流量下钢包内废钢的剩余体积随时间变化关系. （a）100 L·min–1；（b）150 L·min–1；（c）200 L·min–1Fig.15 Residual volume of slab scrap in the ladle varies with time at different argon flow rates: (a) 100 L·min–1; (b) 150 L·min–1; (c) 200 L·min–1

图16 为不同底吹氩气流量下钢包内废钢的剩余体积随时间变化关系. 由图可知，底吹氩气流量为100、150和200 L·min–1时，板形废钢熔化所需时间分别为33、32和31 s，熔化速度分别为2.96、3.06和3.16 cm3·s–1；此时，方形废钢熔化所需时间分别为42、36和34 s，熔化速度分别为2.33、2.72和2.88 cm3·s–1；圆柱形废钢熔化所需时间分别为44、38和35 s，熔化速度分别为2.22、2.57和2.8 cm3·s–1.就圆柱形废钢而言，底吹氩气流量由100上升到150 L·min–1时，废钢完全熔化时间减小了6 s，而底吹氩气流量由150上升到200 L·min–1时，废钢完全熔化时间减小了3 s. 底吹氩气流量由100上升到150 L·min–1时，对废钢熔化影响效果较大，流量由150上升到200 L·min–1时，对废钢熔化影响效果减缓. 随着氩气流量的增加，不同形状废钢的熔化时间均有所减小，尤其是针对比表面积较小的废钢，促进熔化的效果更佳. 说明增加底吹氩气流量，对10 s前的废钢熔化形貌影响不大，但废钢整体熔化速率存在影响.

图16 钢包内不同底吹氩气流量下废钢体积随时间变化曲线Fig.16 Time variation curves of scrap steel volume at different bottom argon flow rates in the ladle

综上所述，底吹氩会显著加快废钢熔化，预热温度对废钢熔化速度的影响程度较底吹氩流量小，且吹氩对比表面积较小的废钢熔化影响较为显著. 结合上述废钢在底吹氩钢包内熔化行为，在生产顺行的前提下，钢包炉内加入较高预热温度和较大比表面积的板形废钢，同时伴随较强的底吹可显著加快废钢的熔化.

4 结论

本文分别对底吹氩钢包内废钢形状、预热温度以及吹氩量对废钢熔化行为的影响机制进行研究，得出如下结论：

（1）底吹氩气可以有效加速废钢熔化，且主要影响废钢远离透气砖的一侧，钢包内随着废钢比表面积的增大，底吹氩气对废钢熔化速度的影响效果在逐渐减缓. 相比较无底吹氩时，200 L·min–1的底吹氩气流量下比表面积分别为120、130.22和160.81 m2·m–3的废钢中心温度升温速率分别提高了7.06、6.51和3.73 K·s–1，熔化速率分别提高了0.92、0.88和0.28 cm3·s–1，完全熔化时间分别缩短了17、15和3 s.

（2）底吹氩钢包内废钢初始温度越高，废钢熔化速度越快，但在有底吹氩气时，废钢预热温度的提高对板形废钢熔化的影响较小. 废钢在底吹氩气流量为200 L·min–1时，板形废钢初始温度为300、500、800和1000 K的完全熔化时间为33、32、31、30 s，板形废钢的熔化速度为2.97、3.06、3.16和3.26 cm3·s–1，即板形废钢初始温度每上升100 K，废钢的熔化速度约提高0.058 cm3·s–1.

（3）底吹氩气流量的增加，可以有效提高废钢的熔化速率，针对比表面积较小的废钢，促进效果更好，相比较底吹氩气流量由100上升到150 L·min–1，由150上升到200 L·min–1对废钢的影响效果有所减缓. 就圆柱形废钢而言，底吹氩气流量由100上升到150 L·min–1时，废钢完全熔化时间减小了6 s，而底吹氩气流量由150上升到200 L·min–1时，废钢完全熔化时间减小了3 s.