基于耗散能演化的层状黄砂岩损伤本构模型及其验证

刘冬桥，郭允朋，李杰宇，凌 凯

1) 中国矿业大学（北京）深部岩土力学与地下工程国家重点实验室，北京 100083 2) 中国矿业大学（北京）力学与建筑工程学院，北京100083

层状岩体在自然界中分布广泛，我国西部大型水电边坡、隧道建设中工程稳定性控制岩层多为层状结构岩体. 受层理结构弱面及倾斜角度影响，层状岩体强度、变形破坏特征与完整岩体差异较大，从室内试验角度研究含层理结构面岩体变形力学特性、损伤发展过程及其本构关系对工程岩体稳定性评价和灾害预警具有重要指导意义[1-2].

许多学者针对板岩、砂岩、千枚岩、页岩等常见层理产状的岩体开展了层理倾角对其各向异性特征影响的试验研究. 例如，邓华锋等[3]研究了层理弱面对砂岩三轴压缩强度、抗剪强度、变形特征和破坏模式的影响效应和机制. Gholami和Rasouli[4]对层状板岩开展单轴、三轴和巴西劈裂试验，发现其弹性参数和强度参数随着层理方向增加呈明显U形分布特征. 胡杰等[5]研究了各向异性层状砂岩在真三轴应力状态下单面突然卸载的应变岩爆破坏特征. 李存宝等[6]、王小良等[7]研究了层理倾角对页岩起裂应力和裂纹损伤应力的影响规律. 杨建明等[8]对不同层理倾角千枚岩开展单轴一次加卸载试验，探讨了层理倾角对千枚岩变形破坏过程中能量演化及岩爆倾向性影响.衡帅等[9]根据层理角度将页岩破坏模式分为张拉劈裂、滑移剪切、贯穿层理和沿层理剪切以及贯穿层理张拉破坏4种模式.

在充分认识层状岩体各向异性特征的基础上，学者们逐渐关注层状岩体损伤演化特征. 比如，腾俊洋等[10]研究发现沿层理弱面分布的原生微裂隙群是层状页岩损伤破坏和劣化的本质. 汪杰等[11]利用节理岩体弹性模量的劣化程度来表征初始节理损伤值，发现初始节理损伤随节理倾角先增大后减小，总体呈现倒“U”型分布规律. 郑广辉等[12]探究了冻融循环条件下层理砂岩损伤发育特征，并建立了考虑层理效应的砂岩冻融劣化模型. 陈子全等[13]以任意时刻耗散能与峰值强度点耗散能的比值为能量损伤指标，分析了层理角度对千枚岩储能能力、释能机制和损伤破裂演化机制的影响. 目前，众多学者从弹性模量[14]、声发射特征参数[15]、裂纹体应变[16]、能量密度[17]等角度建立了多种形式的损伤变量表达式. 由于受载岩石在变形破坏过程中伴随着能量储存、转换与释放，因此，从能量角度建立岩石损伤表达式能够更真实客观反映岩石破裂的内在本质[18]. 在研究层状岩石损伤演化特征的基础上，进一步建立了其损伤本构模型. 孙清佩等[19]对龙马溪组黑色页岩开展动态压缩试验，揭示了层理页岩动载破坏的机制，并建立了综合考虑初始损伤、受荷损伤的层理页岩动载损伤本构模型. 史越等[20]建立了考虑单轴荷载损伤的层状千枚岩损伤本构模型，分析了不同层理角度下千枚岩的损伤演化特征. 寇昊等[21]建立了考虑残余强度的层状岩体损伤本构模型，并分析了不同层理角度岩体的全过程损伤演化规律.

综上所述可知，岩体层理弱面的存在导致其损伤演化规律和本构关系也表现出明显差异性，上述研究成果为分析层状岩体损伤变形破坏过程奠定了较好基础，但还未建立能够模拟和预测层状岩体损伤全过程的理论损伤演化模型，且大多通过定义单一损伤变量来表示层状岩石受荷损伤[20-21]，并未考虑初始层理损伤的影响，由于工程现场层状岩体往往处于多场耦合的地质环境中，导致其变形损伤发展过程更为复杂，因此有必要对层状岩体损伤演化规律及本构关系进一步研究.本文选取工程常见的层状黄砂岩作为研究对象，钻取7种不同层理角度(0°，15°，30°，45°，60°，75°和90°)岩样进行单轴压缩试验，在分析其变形力学特性、破裂模式的基础上，借助基于应变等效假说的弹性模量衰减法表征初始层理损伤变量，从能量耗散角度表征荷载损伤变量，进而得到综合考虑黄砂岩初始层理效应与荷载耦合作用后的总损伤变量，并借助Logistic函数建立了能够描述和预测该损伤发展全过程的理论损伤演化模型，实现了对层状黄砂岩损伤演化全过程统一、完整的描述，进而分析损伤演化规律的层理效应；最后，结合损伤力学与有效介质理论，建立了能够模拟单轴压缩条件下层状黄砂岩变形全过程的分段本构模型，模型形式简单，参数较少且物理意义明确.

1 试样制备与试验方案

1.1 岩样制备

试验样品为云南省楚雄彝族自治州武定县境内广泛分布的层状黄砂岩，具有明显的沉积层理构造. 为充分对比层理倾角对岩样变形力学性质的影响效应，钻取7种(0°，15°，30°，45°，60°，75°，90°)不同层理角度试样，所有试样均取自同一块完整均质岩体，取芯示意如图1(a)所示. 每种角度取3块岩芯，按照相关标准制备成直径50 mm、高度100 mm的标准圆柱体试样，使用砂轮机将试样两个横截面研磨平整，并将所有制备好的试样放置在室外自然条件下风干2周以上. 岩样整体照片如图1(b)所示，可以看出岩样层理结构弱面非常发育且分布均匀. 为方便记录每块岩样试验结果，将岩样按照S-A-B的形式进行编号，S表示黄砂岩，A表示不同层理倾角，B表示该层理倾角下的第B号样品，例如S-0-1，表示层理倾角为0°的第1个样品.

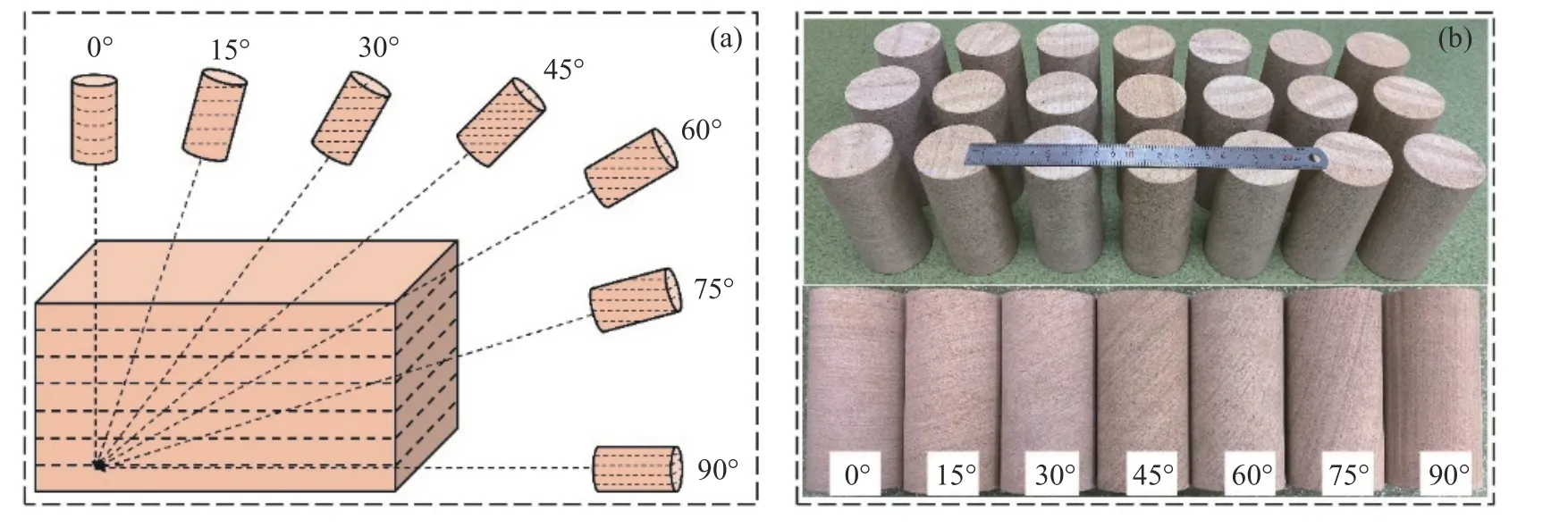
图1 取芯示意及样品图. (a) 试样取芯; (b) 试验样品Fig.1 Schematic of coring and samples: (a) sample coring; (b) test sample

1.2 试验设备与试验方案

开始试验前采用MC-6310非金属超声检测仪测试岩样纵波波速，该设备主要有采集系统、数据连接线和传感器三部分，如图2(a)所示. 为保证声波信号稳定传输和接收，使用凡士林将超声检测仪的传感器与岩样两侧横截面进行耦合处理，再进行波速测试，且每块岩样读取3组数据，求其平均值作为测试结果. 图2(b)为黄砂岩纵波波速随层理倾角的变化关系，其中，v为纵波波速，单位为m·s-1. 从图中可以看出，当层理角度β= 0°时，纵波波速最小，为1400 m·s-1左右，随着层理角度增大，纵波波速呈线性形式逐渐增大，当β= 90°时，纵波波速最大，为1600 m·s-1左右，表明本次试验样品各向异性特征明显.

图2 岩样波速测试. (a) 测试设备; (b) 测试结果Fig.2 Wave velocity testing of rock samples: (a) test equipment; (b) test result

单轴压缩试验在中国矿业大学（北京）深部岩土力学与地下工程国家重点实验室自主研发的T–P（热–力）耦合作用下深部软岩气体运移规律试验系统上进行，如图3(a)所示，该设备可进行单轴加载试验（如单轴压缩、间接拉伸）、常规三轴压缩试验和剪切试验，竖直方向可施加最大压力为2000 kN，侧向可施加最大压力（围压）为100 MPa.系统采用液压伺服控制，实时显示试验加载曲线，并自动记录和存储试验数据. 本次试验采用位移控制方式加载，速率为0.002 m·s-1，直到试样最终破坏后停止试验，试样安装结果如图3(b)所示.

图3 单轴压缩试验. (a) 加载设备; (b) 试样安装图Fig.3 Uniaxial compression test: (a) loading device; (b) sample installation

2 试验结果

2.1 应力-应变曲线

图4 为不同层理倾角黄砂岩单轴压缩应力–应变曲线. 由图4可知，不同层理角度试样从加载到破坏的应力–应变曲线形态基本一致，都经历了初始微裂纹压密、弹性变形、屈服硬化及峰后应变软化破坏4个阶段：(1)初始微裂纹压密闭合. 应力–应变曲线均出现明显非线性上凹形，原因是内部原先存在的张开性软弱结构面、微裂隙等被压缩闭合，该阶段在风化、节理弱化或裂隙化严重的岩石中较明显；(2)弹性变形. 层理倾角的改变导致弹性模量发生变化，表现出各向异性特征；(3)屈服硬化. 微裂纹呈不稳定态势扩展并产生汇合贯通，塑性变形明显，应力–应变曲线明显偏离原有线性变化趋势，不同层理倾角黄砂岩塑性变形阶段差异明显，峰值强度也各不相同，表现出层状岩石的各向异性；(4)峰后应变软化破坏. 当荷载超过试样峰值强度后，岩样内部结构遭到剧烈破坏，大量微裂隙快速扩展，不断交叉贯通形成更多的宏观破裂面，试样强度快速减小.

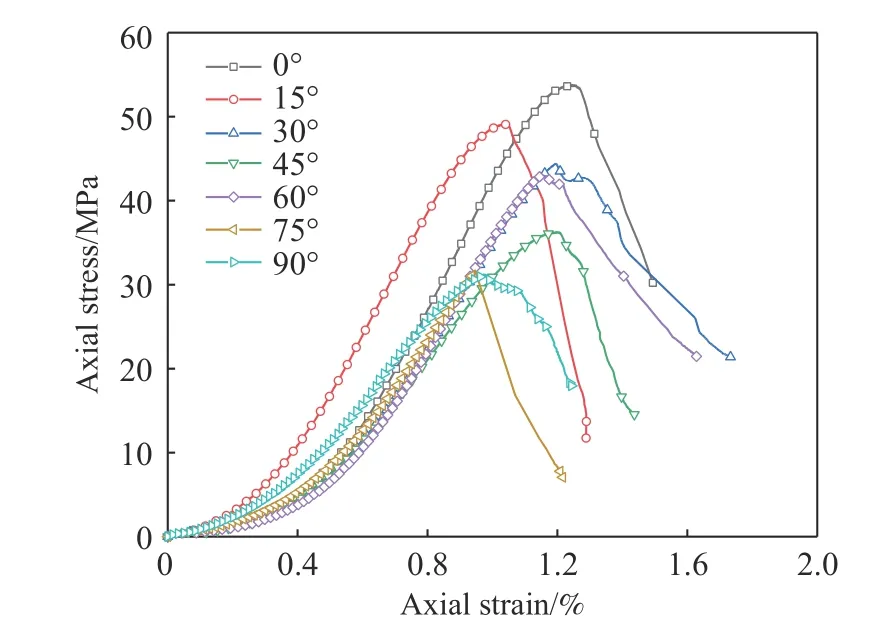
图4 不同层理倾角黄砂岩应力–应变曲线Fig.4 Stress–strain curves of yellow sandstone with different bedding dip angles

黄砂岩峰值强度和弹性模量随层理倾角变化的关系如图5所示. 可以看出，在0°～45°范围内试样峰值强度和弹性模量随层理角度增加均呈现逐渐递减的变化趋势，在45°～90°范围内又表现出先增加后减小的变化趋势，整体变化趋势呈倒“N”型. 所有试样峰值强度均在30～55 MPa之间，弹性模量均在4～8 GPa之间，结合各试样应力–应变曲线峰前初期非线性变形及峰后应变软化特征，表明黄砂岩试样层理弱面强度较低，且层理弱面方向对试样整体变形力学特性产生显著影响. 在0°～45°范围内，荷载方向与层理方向夹角逐渐减小，导致试样所能承受的极限横向拉应力降低，从而弱化了试样峰值强度和弹性模量；层理角度为60°时，结合下一节中试样破裂图片可以看出，主裂纹发展方向与层理方向呈交叉状，表明此时层理面对裂纹发展产生阻碍作用，从而增强了试样变形力学参数；层理角度为75°时，根据其应力–应变曲线和破裂图片可以看出，试样还未产生塑性变形就突然发生沿层理弱面方向的滑动破坏，同样90°试样也是沿着层理弱面方向发生劈裂型张拉破坏，由于层理弱面强度较低，导致试样峰值强度和弹性模量在60°～90°范围内逐渐减小.

图5 黄砂岩峰值强度和弹性模量随层理倾角变化的关系Fig.5 Relationship between the peak strength and elastic modulus of yellow sandstone with changes in bedding angle

2.2 破坏模式

层理倾角对岩样裂缝发展方向及最终破坏模式具有显著影响. 表1为不同层理倾角黄砂岩单轴压缩条件下的破坏形态及素描图，图中灰色虚线表示层理弱面方向，红色曲线表示宏观裂缝的发展轨迹.

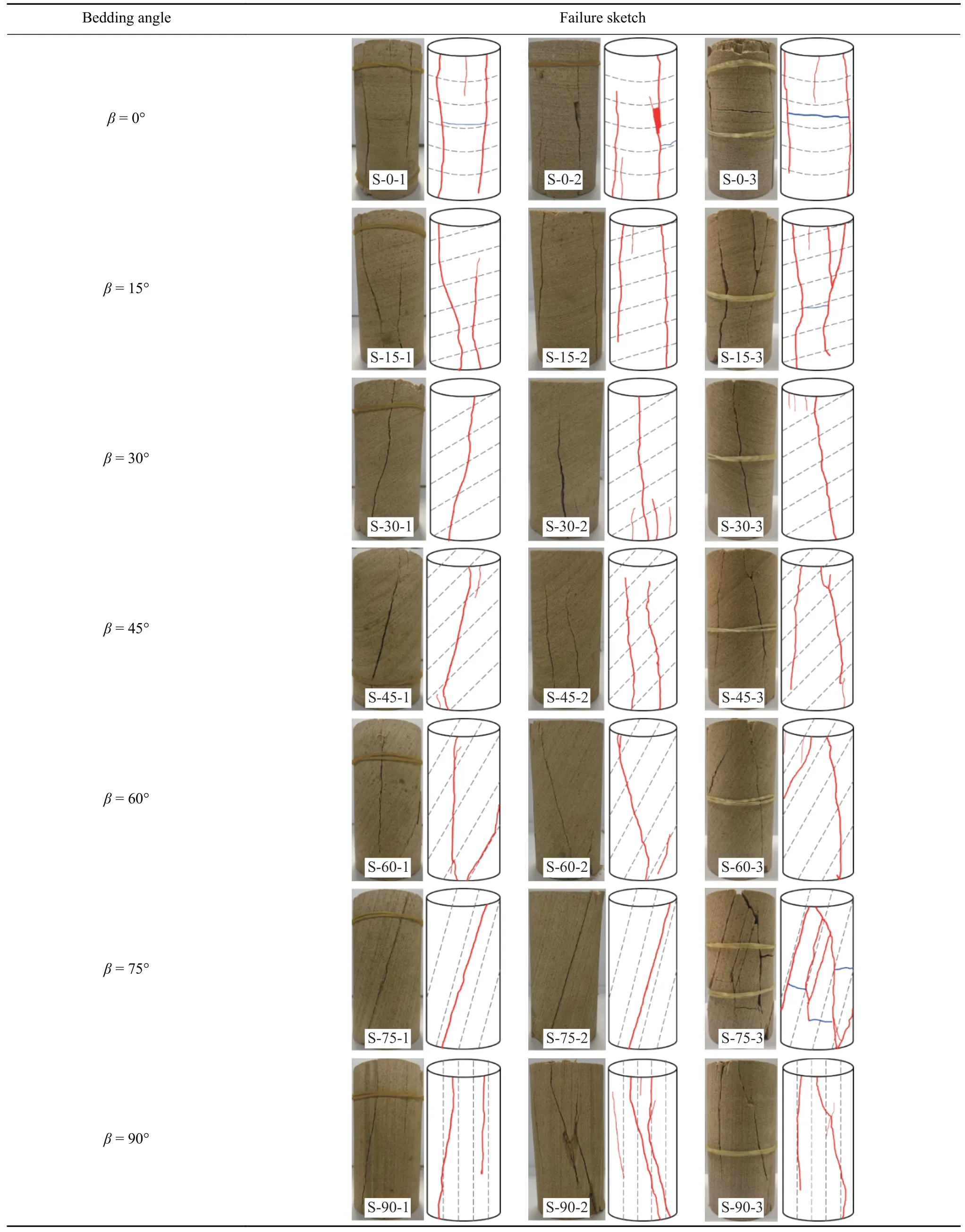
表1 不同层理倾角黄砂岩破坏形态Table 1 Failure modes of yellow sandstone with different bedding angles

由表1可知，层状黄砂岩单轴压缩破坏后形态总体比较完整，裂纹发育充分，发展模式简单且受层理弱结构面的影响明显. 整体上可以发现，当层理角度为0°、15°、30°、45°、60°和90°时，试样宏观主裂纹发展方向均大致与加载方向平行，表现为明显的张拉破坏，这是由于试样在轴向受载过程中存在泊松效应，试样内部产生横向拉应力，当横向拉应力超过试样抗拉极限时，试样产生张拉破坏. 当层理角度为75°时，试样宏观破裂面方向与加载方向呈一定角度，且沿着层理弱面破坏，表现出明显的剪切滑移破坏，这是由于试样层理面强度较低，横向拉应力还未达到极限应力状态，层理面切应力已达到极限应力状态，导致试样沿着层理弱面滑动产生破坏.

层理倾角对单轴压缩试样的裂纹扩展和破坏模式影响较大. 对于大多数试样，裂纹一般从试件顶部中心的加载点延伸到底部，受层理倾角的影响，其损伤破裂轨迹呈现多样化. 对于β= 0°，15°，30°，45°和60°的试样，破坏模式主要受基体中拉伸裂纹的萌生和扩展控制. 对于β= 75°的试样，其破坏模式受层理面剪切裂纹的起裂和扩展控制.β=90°的试样，其破坏模式主要受层理面上拉伸裂纹的萌生和扩展控制. 综上所述，随着层理倾角的增大，层状黄砂岩的破坏模式由基质的拉伸破坏转变为沿层理面的滑动剪切破坏，最后转变为沿层理面的拉伸破坏.

3 层状黄砂岩损伤本构模型

3.1 能量演化

从能量演化角度看，岩石压缩变形破坏过程实质上是外界能量输入、可释放弹性能积聚、能量耗散及释放的一系列复杂演化过程. 从岩石破裂过程的细观角度看，其变形破坏过程又是内部原生微缺陷压缩闭合、新裂纹萌生发展并最终汇聚贯通形成宏观裂缝的过程[13]. 而耗散能的演化过程恰好代表并反映了岩石内部微缺陷及损伤程度演变规律. 典型岩石在单轴压缩条件下总输入能量、弹性能及耗散能随变形增加的演化过程如图6所示. 图中，ε、σ分别为岩石轴向应变和轴向应力，σcc、σcd、σc分别为裂纹闭合应力、损伤应力和峰值应力，εcc为裂纹闭合应变，εcm为裂纹闭合应力点对应的轴向应变值，U表示能量，U0、Ue、Ud分别表示总输入能、弹性能和耗散能，Ud0、Udm分别表示岩石在压密阶段的耗散能和最终完全破坏时刻的总耗散能. 根据能量演化特征，可将岩石损伤破裂演化过程分为四个阶段：

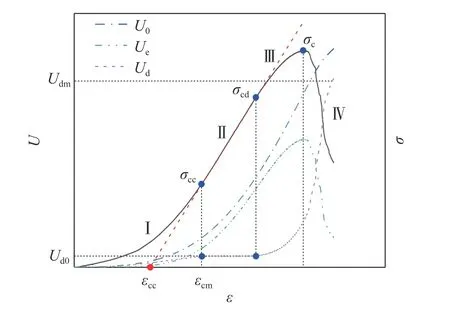
图6 典型岩石变形破坏过程中能量演化曲线 (S-30-2)Fig.6 Energy evolution curve of a typical rock deformation and failure process (S-30-2)

(1) 原生缺陷压密闭合阶段(Ⅰ)：该阶段耗散能曲线先缓慢增加，后逐渐趋于稳定，这是由于岩石内部原生微缺陷、微裂纹受载压缩闭合需消耗少部分能量，当原生裂纹完全闭合时，耗散能曲线趋于稳定.

(2) 无损保持阶段(Ⅱ)：该阶段岩石发生线弹性变形，总能量与弹性能曲线呈平行式发展，耗散能曲线维持稳定水平不变，这是由于原生缺陷完全闭合且几乎没有新裂纹产生，外界做功输入的能量全部以弹性能形式储存在岩石内.

(3) 损伤发展阶段(Ⅲ)：该阶段岩石产生塑性变形，总能量曲线与弹性能曲线开始分叉，耗散能开始不断增加，这是由于新的微裂纹萌生发育需消耗能量，但该阶段大部分外界输入能量仍转化为弹性能.

(4) 损伤加速发展阶段(Ⅳ)：该阶段岩石发生脆性破坏，弹性能曲线急剧下降，耗散能曲线快速增长，这是由于宏观裂缝的形成需消耗更多的能量.

3.2 损伤变量及演化规律

在给定的某一荷载水平下，基于标准化累积耗散能表征的岩石受荷损伤变量[22]为：

式中：Dl为岩石受荷损伤变量，Ud为任意给定ε的应力状态下累积耗散能量值，且Ud∈[0,Udm]. 显然，D= 0时表明岩石完整无损伤，D= 1时表明岩石破坏，完全丧失承载能力.

然而，考虑到岩石峰后还未完全破坏，即还具有一定承载能力，因此引入与残余强度相关的损伤变量修正系数q，式(1)变为：

式中：σr为残余应力.

对于均质完整、硬度高的岩块来说，其初始压密阶段非线性变形不明显，受载后直接进入弹性变形阶段，初始微裂纹压密闭合耗散的能量可以忽略不计. 然而工程实践中经历各种扰动作用后的岩体内部或多或少会含有微裂纹、微裂隙等初始损伤，层理弱面更是岩石原生缺陷的一种特殊表现，从而引起岩石受压变形过程中的裂纹闭合效应[23]. Lim等[24]引入裂纹闭合能来评价岩石内部初始微裂纹损伤程度，即微裂纹压密闭合所耗散的能量（图6中Ud0）. 笔者认为，在借助耗散能演化过程表征损伤变量时应舍去岩石初始压密阶段裂纹闭合摩擦作用耗散的能量，在外荷载未达到裂纹闭合应力之前，初始裂纹压实闭合耗散部分能量，并未有新的裂纹产生，当初始裂纹被压缩闭合后，此时岩石最接近于完整无损、理想弹性状态，弹性变形阶段应变能持续累积，耗散能保持不变，当荷载超过损伤应力，新裂纹开始萌生发育扩展并耗散大部分能量. 因此，忽略初始压密阶段耗散能后，式(2)可变为：

由式(3)计算的受荷损伤变量在裂纹闭合应力之前会出现负值，与实际不符，这里舍去不考虑.以S-30-2试验结果为例，按式(3)可以计算出黄砂岩基于累积耗散能表征的损伤–应变曲线，如图7所示. 可以看出，在不考虑裂纹压密阶段耗散能的条件下，随着轴向应变增大，损伤变量经历了初始无损伤保持、损伤开始和损伤加速阶段，整体呈“S”型发展规律，这分别与岩石弹性变形、塑性变形及应变软化阶段一一对应，表明采用式(3)表征岩石受荷损伤变量演化过程是合理的.

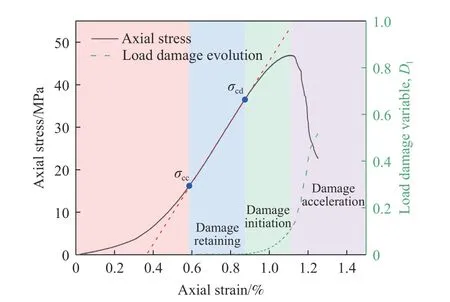
图7 基于累积耗散能的损伤–应变曲线 (S-30-2)Fig.7 Damage–strain curve based on cumulative dissipative energy(S-30-2)

然而，基于累积耗散能计算的损伤变量结果受岩石应力–应变曲线完整性影响，如强脆性岩石峰后应力迅速跌落或试验机刚度不够导致无法准确采集到完整的峰后应力–应变曲线，或是强度较低岩石峰后应变软化还未完全破坏就停止试验，即无法实现对岩石损伤全过程统一、完整的描述.实际上，岩石变形破坏是一个从局部开始、渐进演化的连续性过程，最弱处首先产生缺陷，并不断衍生新缺陷最终导致岩石破坏. 作者在以往研究成果[25-26]中，将岩石损伤演化过程抽象为生物学中某个单种种群的增长过程，并借助生物学中一种简单的增长率随种群大小而变化的连续增长模型，即逻辑斯蒂模型(Logistic model)，建立了能够模拟和预测单轴压缩条件下损伤发展全过程的理论损伤演化模型，实现了对岩石损伤全过程统一、完整的描述. 基于Logistic函数表征的损伤变量表达式如下：

式中，a和r为损伤演化方程拟合参数.

式(4)可进一步变换为：

结合式(3)和式(5)可拟合获得参数a和r的值，将其代入式(4)即可得到受荷条件下岩石理论损伤演化方程. 然而，层理弱面的存在会导致岩石产生一定程度初始损伤，进一步劣化岩石变形力学性能[23]，如弹性模量和峰值强度等. 考虑到复杂地质作用后岩体内部形成初始损伤，诸多学者通过室内试验模拟研究了高温热处理[27]、节理弱面倾角[11]等不同初始条件对岩体变形力学特性及损伤破坏过程的影响. 目前，表征初始损伤的方法主要有弹性模量衰减法[11,27-31]、能量耗散法[32]、超声波波速法[33-35]及声发射特征参数[33-35]等. 岩体内部由于高温作用、节理、层理、孔隙等导致的初始损伤比较复杂，这些初始缺陷在一定程度上弱化了岩体强度和弹性模量，而岩体宏观物理性能的响应能够代表材料内部的劣化程度，因此可以运用宏观唯象损伤力学方法来研究岩体的初始损伤，由于岩体弹性模量较易分析和测量，使得诸多学者广泛采用弹性模量的劣化程度来表征岩体不同条件下的初始损伤值. 本文参考该思路，得到不同层理倾角黄砂岩在受载前的初始损伤变量Dβ为：

式中：Eu为完整无损条件下岩石的初始弹性模量；Eβ为层理倾角为β的岩石弹性模量，β为层理面与水平面之间的夹角.

然而完整无损条件下的岩石弹性模量几乎难以准确获得. 根据三轴压缩试验可以发现，侧向压力的存在会弱化岩石压密阶段非线性特征，随着围压不断增大，岩石初始压密阶段非线性变形越来越不明显，弹性模量也呈现非线性增大规律，当围压增大到一定程度时，岩石内部原生缺陷或裂隙被压缩闭合，初始损伤程度减弱并逐渐接近理想完整无损状态，此时岩石轴向应力–应变曲线会直接进入线弹性阶段，可假设此时岩石不具有初始损伤，这说明增大围压能够起到消除初始缺陷的作用. 张超等[30]采用特定围压下含初始缺陷岩石弹性模量代替完整无损条件下岩石弹性模量建立了初始损伤的确定方法. 由于0°时黄砂岩峰值强度和弹性模量最大，说明该角度是初始损伤程度相对最弱的，本文对层理角度为0°的黄砂岩试样进一步开展围压分别为5、10和15 MPa的常规三轴压缩试验，发现围压为15 MPa时，偏应力–应变曲线直接进入弹性变形阶段，几乎不发生初期的非线性压密变形，表明此围压下黄砂岩接近初始无损伤状态，因此，利用此围压条件下的弹性模量代替完整无损条件下黄砂岩的弹性模量，即Eu=12.97 GPa.

进一步，结合损伤力学理论可得到黄砂岩层理、荷载耦合总损伤变量表达式[11]为：

式中：Dt为黄砂岩层理、荷载耦合作用后的总损伤变量.

将式(4)和式(6)代入式(7)可得：

式(8)即为本文建立的考虑层理效应的黄砂岩理论损伤演化方程，对式(8)分别求一阶导数和二阶导数，还可得到损伤演化速率方程和损伤加速度方程：

以S-30-2试验数据为例，按照如下步骤可实现对层状黄砂岩单轴压缩下损伤演化曲线的统一完整描述和预测：

(1) 根据层状黄砂岩单轴压缩应力–应变试验数据计算得到耗散能演化曲线，确定裂纹闭合能Ud0和总耗散能Udm，进而结合式(3)计算出各数据点所对应的荷载损伤变量值Dl.

(2) 舍去裂纹闭合应力之前损伤变量为负值的不合理部分，利用式(5)进行线性拟合得到参数a和r的值，进而得到基于Logistic函数表征的荷载损伤变量表达式.

(3) 根据应力–应变试验曲线弹性变形阶段斜率确定不同层理倾角黄砂岩弹性模量Eβ，代入式(6)得到层状黄砂岩初始层理损伤变量Dβ.

按照上述步骤，结合式(8)、式(9)和式(10)可得到基于Logistic函数考虑黄砂岩层理效应的理论损伤演化曲线、损伤演化速率曲线及损伤加速度曲线，如图8所示. 由图8可知，理论损伤演化曲线是呈“S”型发展规律，损伤演化速率曲线表现出关于应变的对称分布特性，且总体呈现正态分布规律，其峰值点即为岩石最大损伤演化速率，记为D′m，该值越大，对应损伤演化曲线越陡，损伤演化速度越快. 在达到拐点前，损伤速率随应变增加而增大，称为正加速期；在拐点之后，损伤速率随应变增加而减小，称为负加速期. 损伤演化方程二阶导数曲线的极大值点和极小值点分别对应损伤演化曲线上损伤加速点B与损伤减速点C. 根据损伤演化曲线中的四个关键点——损伤起始点A、损伤加速点B、损伤减速点C和损伤终止点D，可将岩石理论损伤演化曲线划分为初始损伤保持(Ⅰ)、损伤开始(Ⅱ)、损伤加速(Ⅲ)、损伤减速(Ⅳ)及损伤终止(Ⅴ)5个阶段，这与借助宏观参量表征的损伤演化过程是一致的[25].

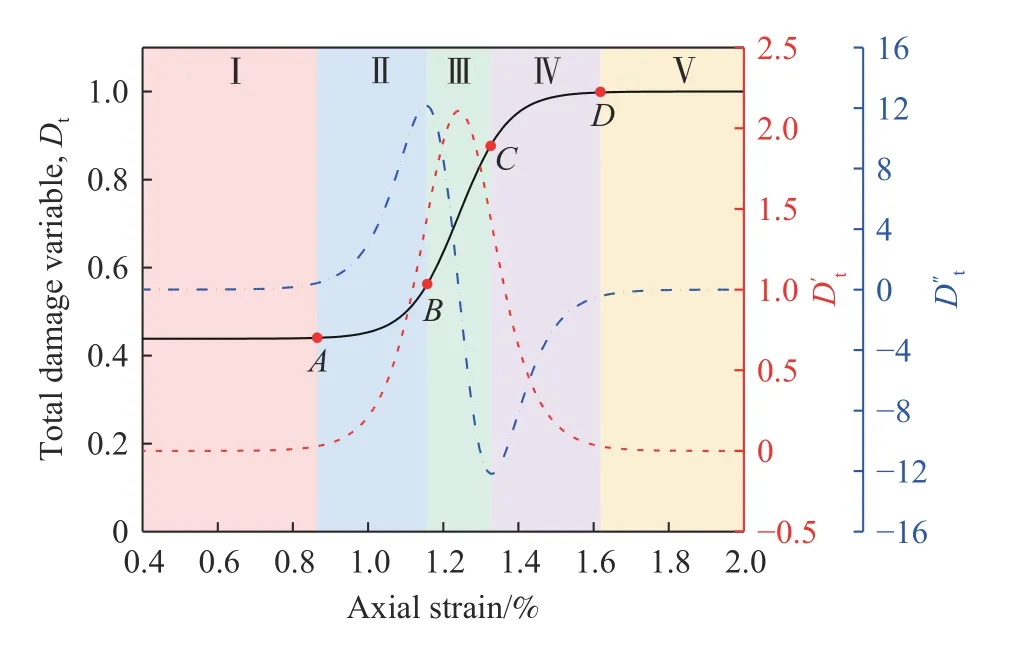
图8 基于Logistic函数的标准S型曲线Fig.8 Standard S-curve based on the logistic function

表2统计了不同层理倾角黄砂岩理论损伤演化方程中所需参数的值，其中相关性系数R2按下式计算：

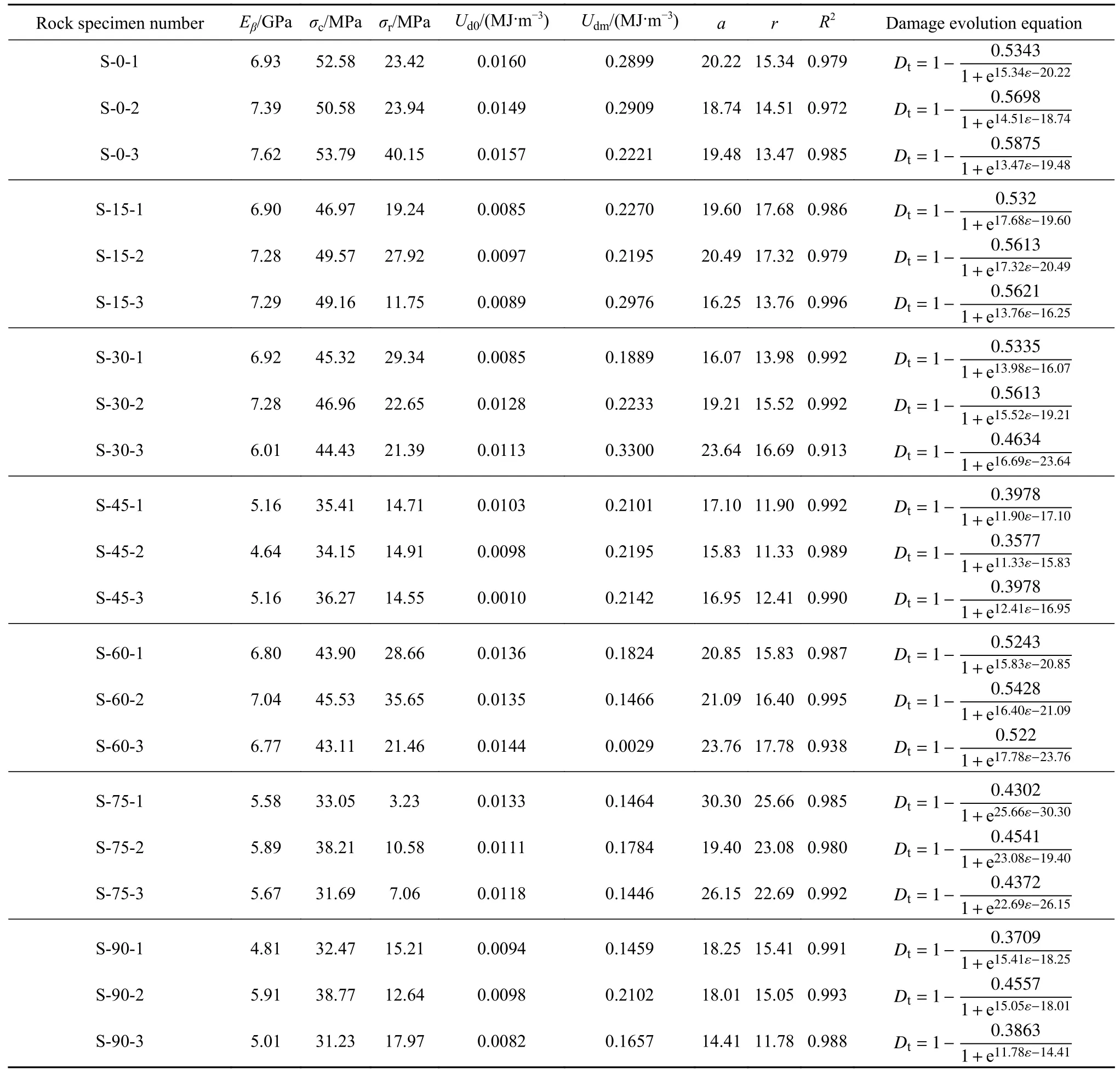
表2 拟合参数及损伤演化方程Table 2 Fitting parameters and damage evolution equations

式中：Dtest为任意时刻实际计算的损伤变量值，Dpre为损伤模型预测值，Dave为实际计算损伤变量的平均值，n为任意时刻试验测点数据，其最大值为累计测点数据量. 相关性系数越大，表明理论值与实际值偏差越小.

由表2可知，21个函数拟合结果中相关性系数最小值为0.913，最大值为0.996，平均值为0.982，这说明基于Logistic函数得到的理论损伤演化曲线与实际损伤结果吻合度高，表明基于Logistic函数建立的损伤演化方程能够很好的描述层状黄砂岩变形破坏损伤变量演化过程. 根据表2中不同层理倾角黄砂岩力学参数及式(6)，可得到层理倾角与初始层理损伤之间的内在关系，如图9所示.由图9可知，层状岩体存在初始损伤，且其初始层理损伤程度随层理倾角呈现先增大后减小再增大的趋势，在0°时达到最小值，在45°时达到最大值，整体呈“N”型分布规律. 当层理倾角为0°时，初始层理损伤平均值约为0.436，当层理倾角增加至45°时，初始层理损伤平均值约为0.615，增长率约为41.06%，当层理倾角继续增大至60°时，其初始层理损伤平均值减小至0.47，随着层理倾角继续增大至90°，初始层理损伤又继续增加至0.596，较60°时初始层理损伤增加26.81%. 此外，初始层理损伤最大值与最小值之比达到1.41，表明层理倾角对层状岩体初始损伤影响较大.

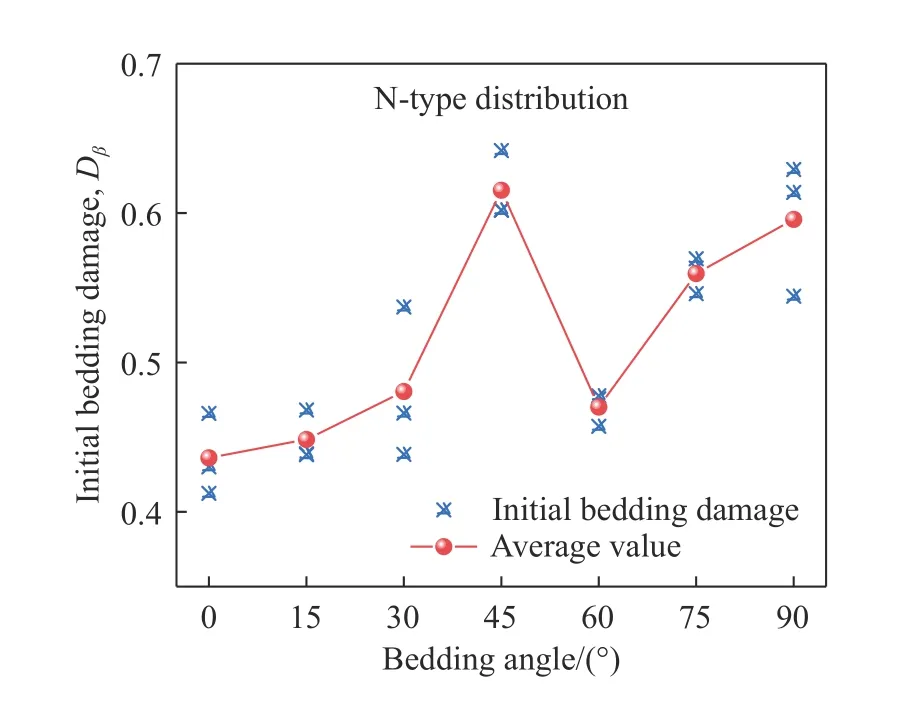
图9 初始层理损伤与层理倾角关系Fig.9 Relationship between initial bedding damage and bedding angle

根据表2中不同层理倾角黄砂岩损伤演化方程可以得到其对应的理论损伤演化曲线，限于篇幅仅列举不同层理角度中典型结果进行比较，如图10所示. 由图10可知，不同层理倾角黄砂岩存在不同程度的初始损伤，理论损伤演化曲线发展趋势基本一致，均经历了初始损伤保持、损伤开始、损伤加速、损伤减缓及损伤终止5个阶段，呈“S”型发展规律，这与以往研究结果是一致的[11].

图10 不同层理倾角黄砂岩理论损伤演化曲线Fig.10 Theoretical damage evolution curve of yellow sandstone with different bedding angles

为定量分析层理倾角对黄砂岩损伤演化规律的影响，统计了黄砂岩理论损伤演化速率曲线峰值点即最大损伤演化速率D′m随层理倾角的变化关系，如图11所示. 由图11可知，倾角为75°时，D′m最大，平均值约为2.62，这是由于75°岩样突然沿层理弱面发生剪切滑移破坏，其峰后应力–应变曲线表现为脆性快速跌落；45°时D′m最小，平均值约为1.14，表明该倾角损伤发展速度最慢，是本次层状黄砂岩最有利角度. 在7组不同层理倾角黄砂岩试样中，最大损伤演化速率D′m最大值与最小值之比约为2.3，表明层理倾角对层状岩体损伤演化规律影响较大，即层理弱面的存在导致岩体损伤演化规律表现出显著各向异性.

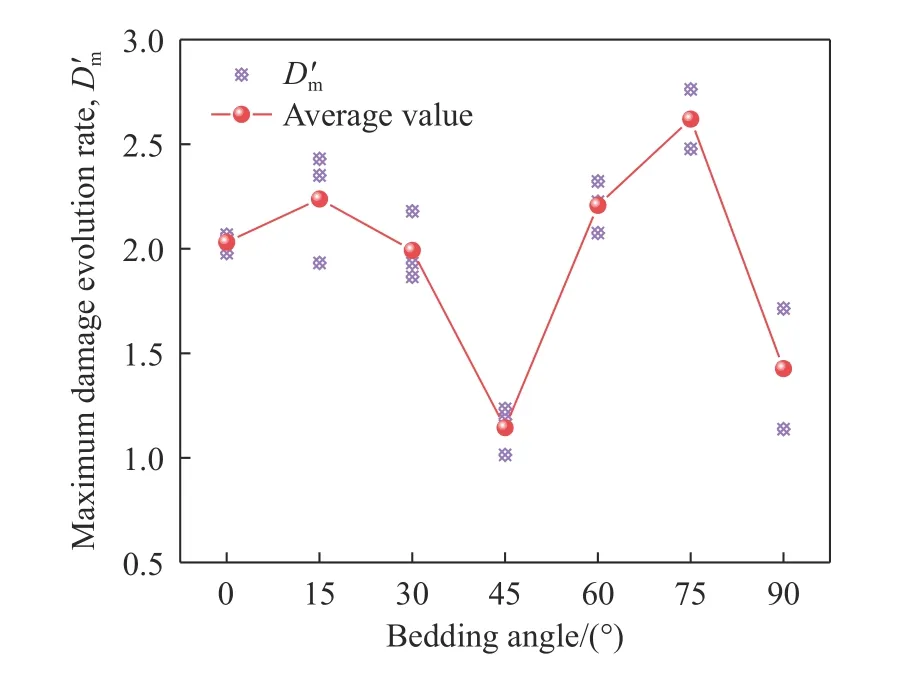
图11 最大损伤演化速率与层理倾角关系Fig.11 Relationship between maximum damage evolution rate and bedding angle

3.3 本构模型及验证

由Lemaitre应变等效假说和式(8)即可得到单轴压缩条件下基于Logistic函数考虑黄砂岩层理倾角效应的损伤本构关系表达式为：

需要注意的是，本文在3.2节中借助耗散能表征荷载损伤变量时未考虑微裂纹压密闭合阶段所耗散的能量，即假定岩石受荷后不产生初始压密非线性变形，直接进入线弹性变形阶段，因此，还需从总应变中减去裂纹闭合应变来获得校正应变，故式(12)变为：

以S-30-2试验结果为例，根据式(13)得到的理论本构关系与试验数据对比如图12所示，可以看出，理论本构曲线能够很好的描述岩石弹性变形、塑性变形及峰后应变软化过程，且破坏时刻峰值应变和峰值强度也得到了可靠预测，不足的是，根据式(13)得到的理论本构关系初期应力从负值开始增加，与实际试验数据仍存在较大差距，无法描述层状黄砂岩初始压密阶段的非线性变形特征，这是由于应变等效性假说没有考虑岩石初始损伤导致的压实效应. 而岩石在漫长复杂的成岩过程中及外界各种复合扰动（温度、湿度、高地应力）作用下，其内部或多或少会产生孔隙、裂隙、节理弱面、断层等原生缺陷，正是这些初始缺陷的存在导致岩石应力–应变曲线初期表现出强烈的非线性，进而影响岩石的抗压强度、弹性模量等变形力学参数. 因此，还需对式(13)进行修正.

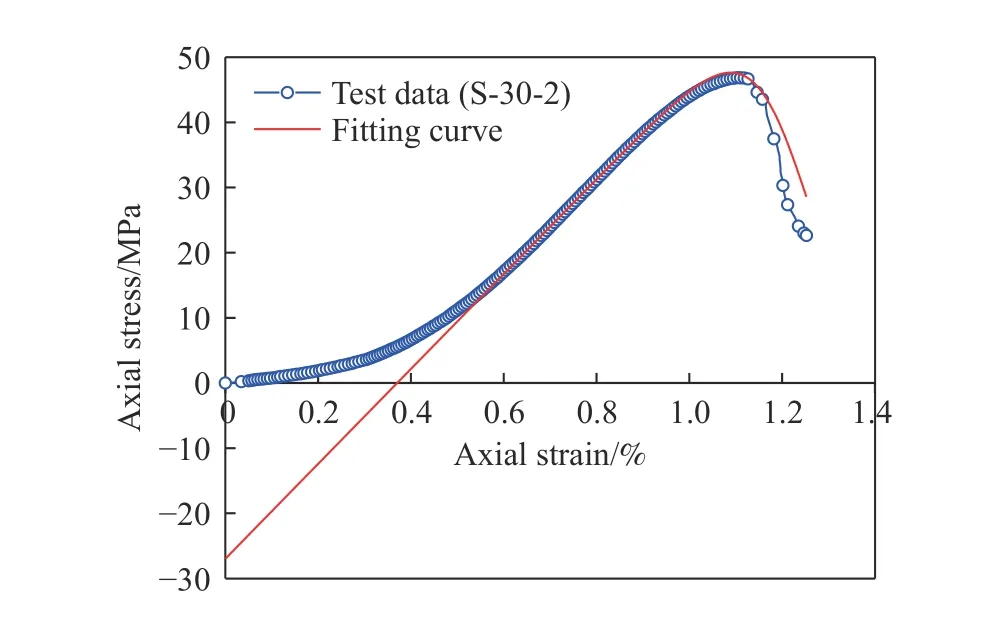
图12 理论本构关系与试验数据比较 (S-30-2)Fig.12 Comparison of the theoretical constitutive relation and test data(S-30-2)

基于有效介质理论，可将岩石轴向变形ε分为基体变形εm和裂纹变形εc两部分[23]：

典型岩石在损伤应力前的变形过程如图13所示. 在单轴或三轴压缩试验前期，岩石内部原生微裂隙或裂纹随荷载增加被逐渐压缩密实，该阶段裂纹变形量大小及裂纹变形曲线下凸程度受岩石内部赋存裂纹的数量、密度和几何特征等因素影响；当裂纹变形曲线趋于稳定不再增长，岩石变形主要由基体产生的线弹性变形组成，该阶段原生微缺陷被完全压密且没有新的微裂纹萌生，此时岩石近似完整刚性体；当荷载继续增加超过岩石屈服强度时，新的微裂纹开始萌生发育，岩石随后进入微裂纹稳定以及不稳定发展阶段.

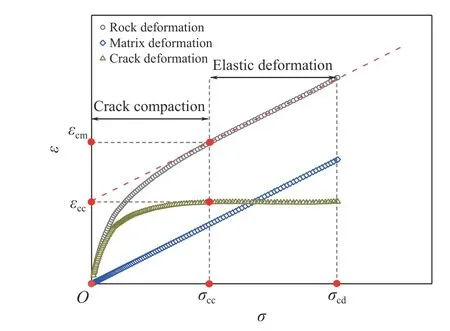
图13 典型岩石峰前变形示意图 (S-30-2)Fig.13 Schematic of typical rock pre-peak deformation (S-30-2)

岩石基体可近似为连续性固体材料，其变形过程遵循广义虎克定律，即：

结合式(14)和式(15)可得：

岩石基体发生弹性变形，而微裂纹发生非线性变形，左建平等[36]基于变弹性理论推导了单轴压缩条件下煤岩组合体裂纹压密变形阶段的非线性规律，并建立了轴向微裂纹闭合模型：

式中：εcc为裂纹闭合应变，可根据应力–应变曲线弹性段反向延长线与横轴交点确定；Ecc为裂纹闭合阶段等效弹性模量，可根据图13中裂纹应变–应力曲线拟合获得.

图14为不同层理倾角黄砂岩裂纹变形试验数据与拟合曲线比较. 可以看出，轴向裂纹闭合模型能够较准确的模拟和反映岩石初始压密阶段非线性变形特征.

图14 裂纹变形拟合结果与试验数据对比Fig.14 Comparison between the fitting results of crack deformation and test data

进一步，结合式(14)、(15)和(17)可得到层状黄砂岩初始压密阶段的本构关系式：

最终，结合式(13)和(18)，以图13中裂纹闭合应力σcc对应的轴向应变εcm为临界点，得到了考虑层状黄砂岩初始压密阶段非线性变形特征的分段本构模型：

为验证本文所建模型合理性和可靠性，基于层状黄砂岩单轴压缩试验结果，按照前述步骤即可计算获得模型所需参数，将所有参数代入式(19)，即可获得两个阶段的本构关系表达式，见表3.图15为理论本构关系曲线与试验数据对比结果.从图中可以看出，本文建立的分段本构模型能够很好的描述层状黄砂岩单轴压缩条件下应力–应变全过程. 应力–应变曲线峰前与峰后过程均能较好的描述，尤其是峰前初始压密阶段非线性变形特征、线弹性变形、塑性变形及峰值应力均得到准确可靠的体现，峰后应变软化过程描述良好，整体上能够反映单轴压缩条件下层状黄砂岩的变形力学行为，验证了本文所建模型的合理性和可靠性.

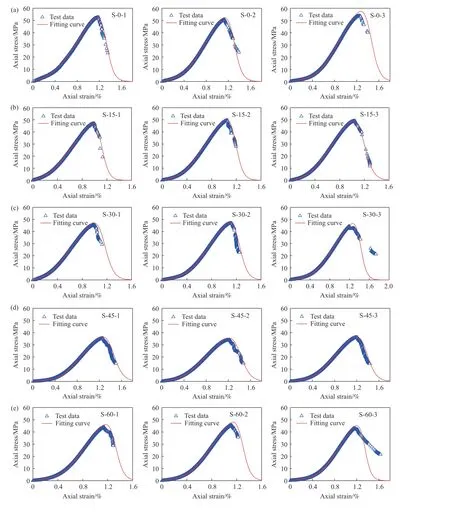
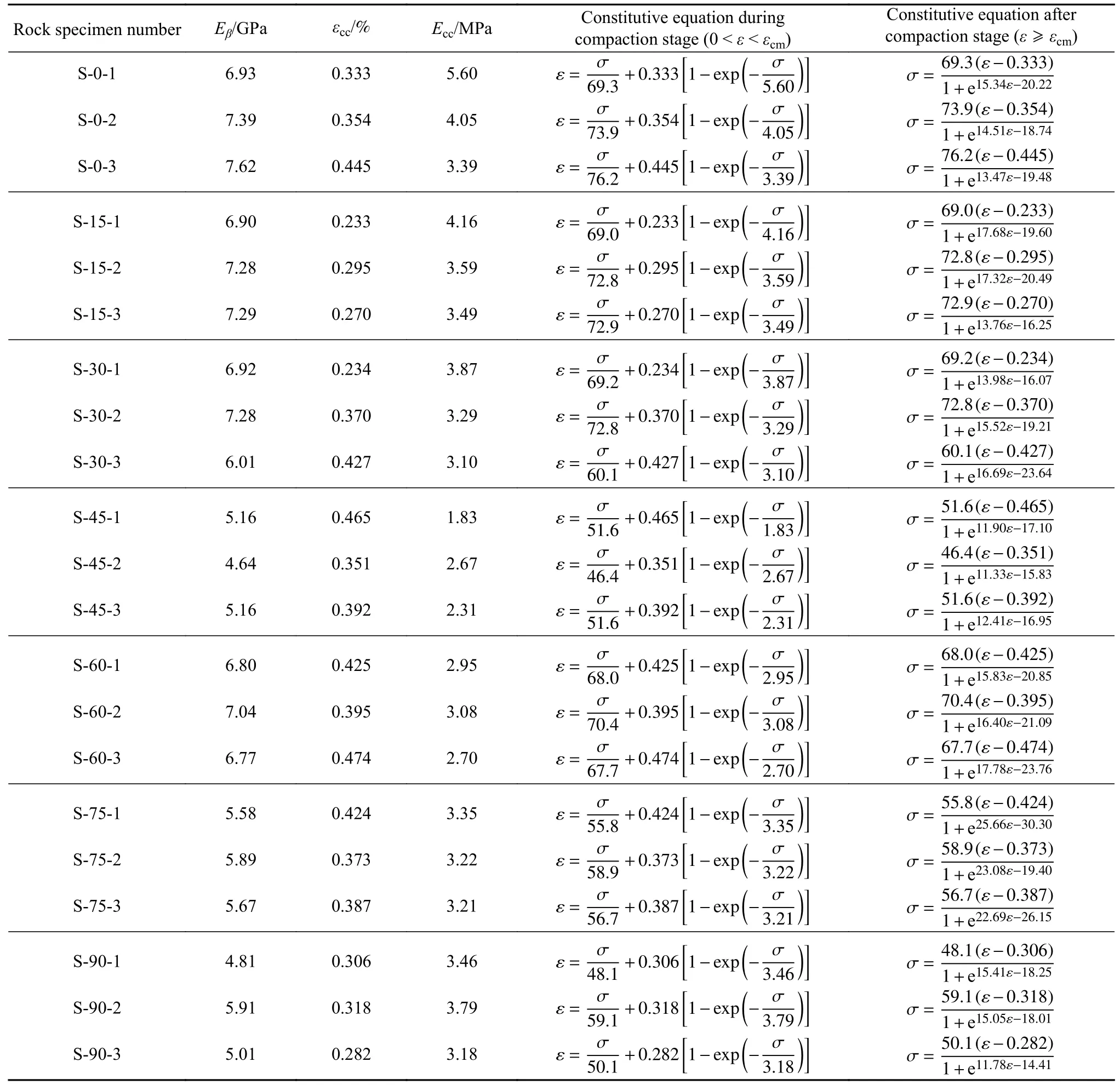
表3 模型参数及本构方程Table 3 Model parameters and constitutive equations

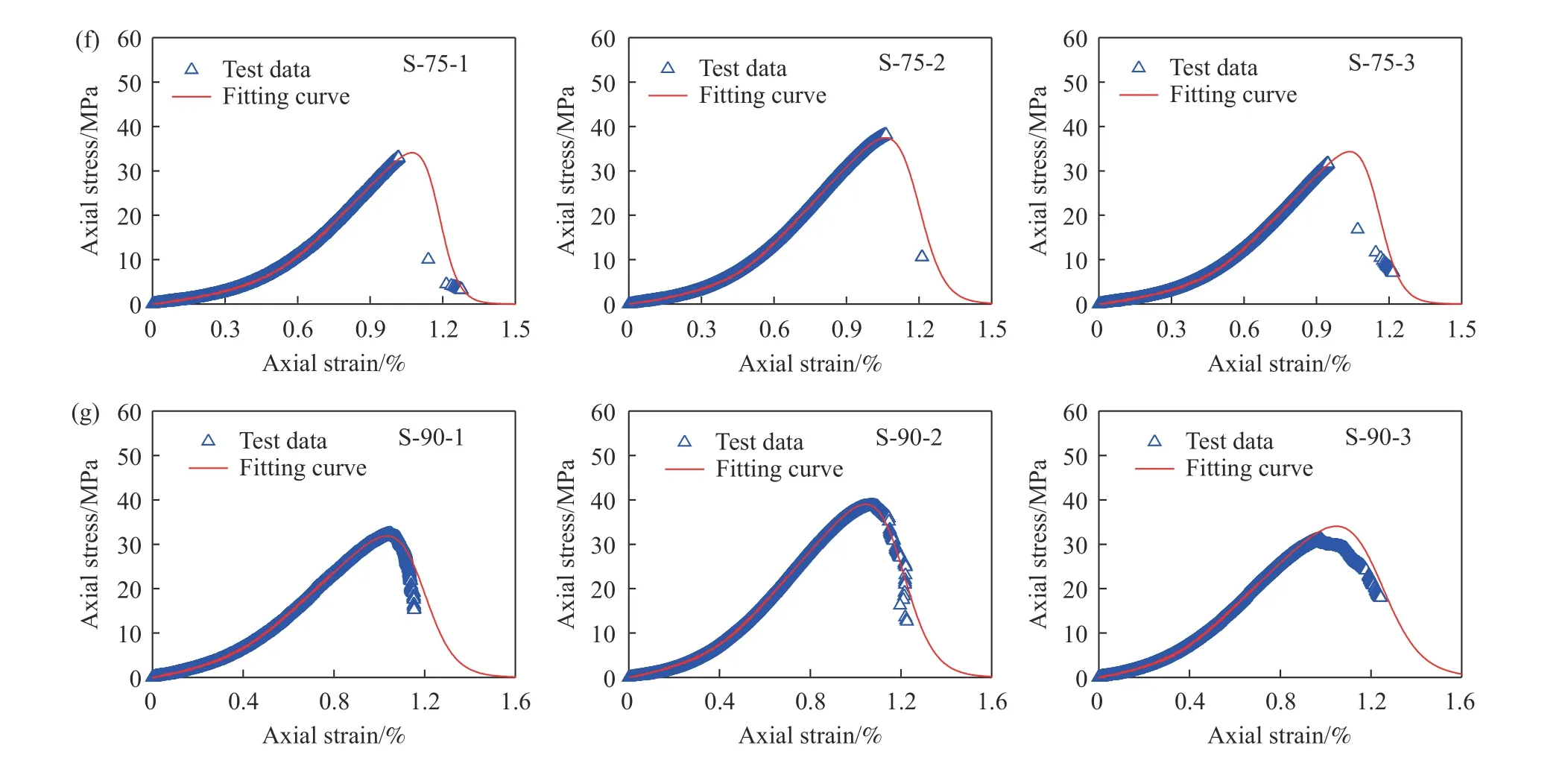
图15 试验数据与本构模型拟合曲线比较. (a) β = 0°; (b) β = 15°; (c) β = 30°; (d) β = 45°; (e) β = 60°; (f) β = 75°; (g) β = 90°Fig.15 Comparison between test data and fitting curves of the constitutive model: (a) β = 0°; (b) β = 15°; (c) β = 30°; (d) β = 45°; (e) β = 60°; (f) β = 75°;(g) β = 90°

3.4 模型参数分析

在对模型验证的基础上，从损伤演化和本构关系两个角度对本构参数物理意义进行讨论分析，进一步验证模型的合理性. 以S-0-1试验结果为例，保持本构模型中弹性模量Eβ和裂纹闭合应变εcc不变，通过改变a和r的值来分别研究.

（1）参数a、r对损伤演化过程的影响.

保持参数r=15.34不变，改变参数a的值，得到参数a对损伤变量和损伤演化速率–应变曲线的影响结果，如图16所示；保持参数a=20.22不变，改变参数r的值，得到参数r对损伤变量和损伤演化速率–应变曲线的影响结果，如图17所示. 由图16和图17可知，参数a反映岩石初始损伤程度，a值越大，初始损伤程度越低，达到开始损伤状态变形量越大，但损伤演化过程及其演化速率曲线形式不变，故达到接近完全损伤及最大损伤演化速率状态的变形量也随之增大，且最大损伤演化速率D′m保持不变；参数r反映损伤演化速度的快慢，r值越大，达到加速损伤及最大损伤演化速率状态的变形量越小，损伤变量向接近完全损伤状态演化速度越快，即损伤变量-应变演化曲线越陡峭，损伤演化速率曲线越尖锐且最大损伤演化速率D′m也越大.

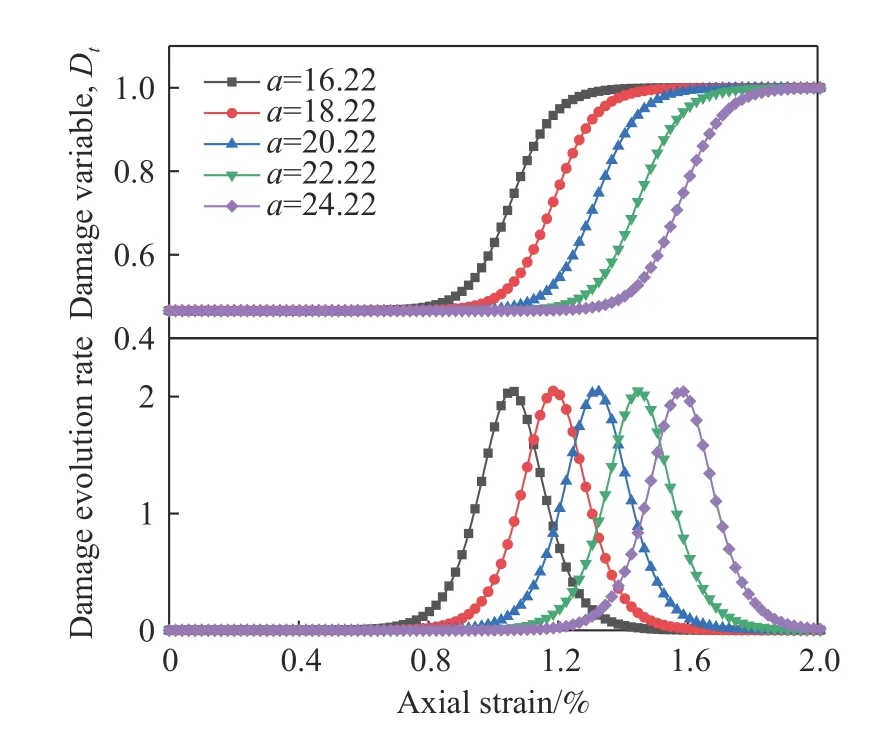
图16 参数a对损伤演化规律的影响 (r=15.34)Fig.16 Effect of parameter a on damage evolution (r = 15.34)

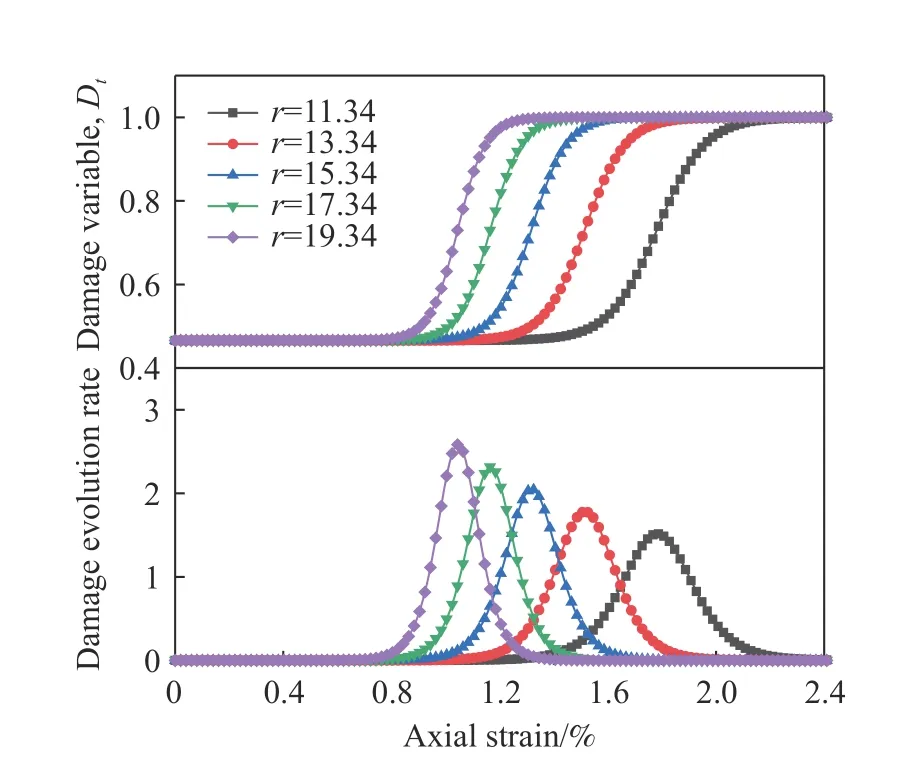
图17 参数r对损伤演化规律的影响 (a=20.22)Fig.17 Effect of parameter r on damage evolution (a = 20.22)

（2）参数a、r对本构关系的影响.

保持参数r=15.34不变，改变参数a的值，得到参数a对本构关系的影响结果，如图18所示；保持参数a=20.22不变，改变参数r的值，得到参数r对本构关系的影响结果，如图19所示. 由图18和图19可知，参数a和r均对岩石本构关系产生显著影响. 参数a越大，单轴抗压强度及峰值应变越大，峰后应力跌落速率随参数a增大呈非线性增加，即峰后脆性破坏程度越强；参数r越大，单轴抗压强度和峰值应变反而越小，参数r对峰后应力跌落速率几乎没有影响，即不改变应力–应变曲线形态和脆性程度.

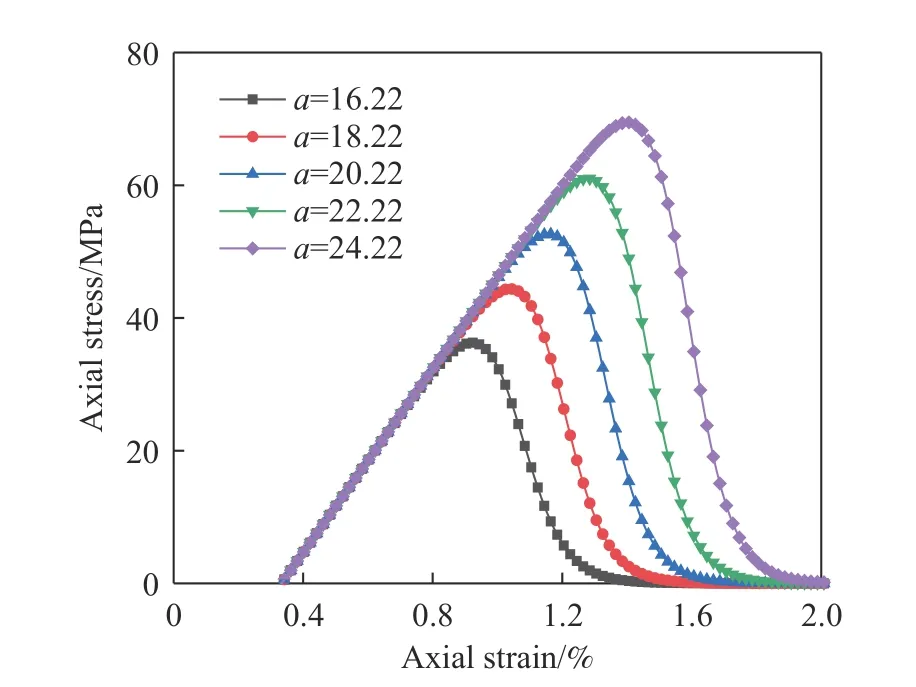
图18 参数a对本构关系的影响 (r=15.34)Fig.18 Effect of parameter a on the constitutive model (r = 15.34)

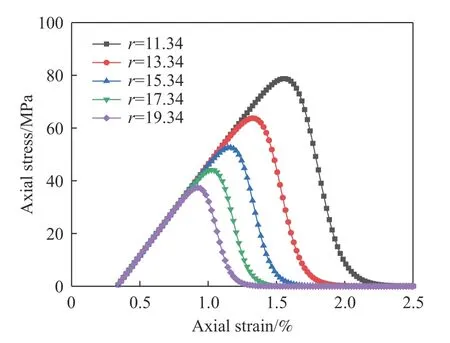
图19 参数r对本构关系的影响 (a=20.22)Fig.19 Effect of parameter r on the constitutive model (a = 20.22)

综上所述，本文所建本构模型中参数a和r物理意义明确，共同决定理论应力–应变曲线的形态，更加证明了模型的合理性和可靠性.

4 结论

(1) 基于耗散能表征的层状黄砂岩损伤演化曲线整体呈“S”型变化趋势，可分为初始无损伤保持、损伤开始、损伤加速及损伤减速终止4个过程.

(2) 借助Logistic方程建立了能够描述基于耗散能表征的层状黄砂岩损伤演化过程的函数表达式，且拟合性较好，平均拟合度为0.982，实现了对损伤演化全过程完整统一的模拟和预测.

(3) 在上述损伤演化方程的基础上，结合有效介质理论，进一步得到层状黄砂岩单轴压缩损伤本构关系，理论本构曲线与试验数据吻合度高，试样峰值强度和峰值应变均得到较准确描述，具有很好地适用性，且模型参数少、物理意义明确，表达较为简单.

(4) 通过对本构模型中参数a和r的不同取值比较分析发现，参数a反映岩石初始损伤程度，a越大，初始损伤程度越低，峰值强度越高；参数r反映损伤演化速度，r越大，损伤变量发展速度越快，最大损伤演化速率越大，且所建本构模型理论曲线形状由参数a和r共同决定.