一种环境振动源强预测随机可靠度分析方法

张校恺, 韦 凯

(西南交通大学 土木工程学院,成都 610031)

近年来,随着国家经济与城市轨道交通领域不断发展,截至2021年,我国城市轨道交通线路总运营里程达9 724.35 km(含港澳台),排名世界第一[1]。密集的城市轨道交通网络在给人们带来交通便利的同时,其所带来的环境振动噪声也无时无刻不在影响着周围居民的日常生活、干扰附近精密仪器的运作甚至对沿线的历史建筑产生破坏[2-3],随着《中华人民共和国噪声污染防治法》的实施,高要求的减振降噪已成为城市轨道交通发展面临的一项重大挑战[4]。然而,近年来对减振投资的增加并没有达到预期的效果,环境振动超标与居民投诉的情况仍然存在[5]。

环境振动源强的精准预测是减振降噪精准设计的前提,根据适用阶段的不同分为3个等级,分别是初步预测、确认预测及精准预测。其中初步预测适用于可行性研究阶段,主要任务是识别振动敏感点,是后续工作的基础。我国环境振动源强初步预测主要通过HJ 453—2018《环境影响评价技术导则 城市轨道交通》[6](后简称为《18导则》)中的经验修正项对拟建工程断面源强进行类比预测。然而,环境振动源强并非是一个定值,而是具有随机不确定性的变量,即使在同一条线路相同区间的2个测试断面的测试结果也有超过15 dB的差异[7-8];况且不同线路之间工程条件存在较大差别,经验修正项在不同线路预测结果的准确度必然也具有随机不确定性,准确度不足将导致筛选敏感点时出现多选、错选及漏选的情况,其中多选和错选的敏感点虽可通过后续的确认预测和精准预测排除,但会浪费大量的时间成本,漏选则会导致部分敏感点振动超标,不得不进行线路改造从而浪费大量经济成本。

众多学者针对源强的随机不确定性开展了相关研究,最常用的随机振动分析方法包括蒙特卡罗(Monte Carlo,MC)法[9]、随机摄动法[10]、正交展开理论[11]以及概率密度演化理论[12]。MC法作为其中最常用的随机分析方法,是通过对大量的随机样本的统计分析得到一个与真实情况相接近的统计特征值,具有较高的计算精度,但由于该方法要求数据必须具有较大的样本容量,因此需要花费大量计算时间。

为了弥补MC法耗时的缺点,本文基于车辆-轨道耦合动力学原理,建立了具有较高计算效率的车辆-轨道-盾构隧道耦合振动模型,后基于MC法提出了一种环境振动源强预测随机可靠度分析方法,以《18导则》源强预测轴质量和簧下质量修正项CW、轮轨条件修正项CR及隧道型式修正项CT为例,以85%为目标可靠度研究了其在不同工程条件下预测结果的准确度,分析了导致修正项预测准确度具有随机不确定性的主要因素并提出了相应的标准化管理建议。有利于完善我国城市轨道交通领域设计、运营管理标准,从而提高《18导则》半经验模型源强预测的准确度,实现环境振动敏感点的精准筛选,节约减振成本,促进城市轨道交通绿色发展,具有一定的工程价值与意义。

1 车辆-轨道-盾构隧道耦合模型

基于车辆-轨道耦合动力学原理,建立了可以直接反映隧道壁振动水平的车辆-轨道-盾构隧道耦合振动模型,并与实测数据进行对比,验证了模型的准确性。

1.1 振动方程

仿真模型(图1)从上到下包括车辆、轨道及隧道3个子系统。其中车辆系统简化为具有10个自由度的多刚体模型,轨道简化为无限长的欧拉梁,扣件简化为离散点支撑,车辆与轨道系统的振动微分方程详见文献[13]。将隧道简化为有阻尼弹性地基上的无限长欧拉梁。夏禾[14]指出,当天然土体的应变ε<1×10-4时,土体的变形为弹性变形,不需要考虑土体的非线性特征,而轨道交通引起的自由场振动引发的土体剪应变通常小于1×10-5,所以可以将基底土层简化考虑为连续线性弹簧。

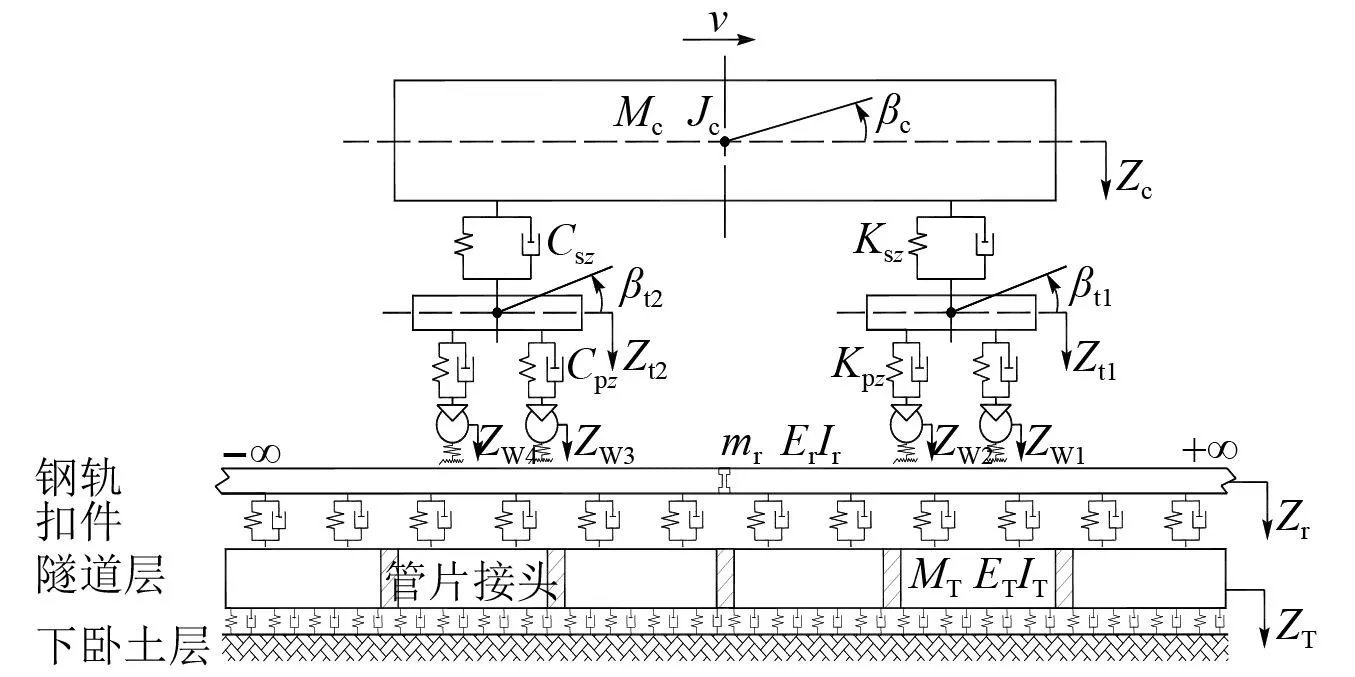
图1 模型示意图Fig.1 Model diagram

引入隧道正则振型坐标qT(t),其垂向振型ZT(x)与隧道的垂向振动微分方程见式(1)～式(2)。

(1)

(2)

式中:ET为隧道的弹性模量;IT为隧道的截面惯性矩;η为盾构隧道的纵向等效抗弯刚度有效率,根据文献[15]建议取值为0.176～0.044;mT为隧道每延米质量;NM为隧道截取模态阶数;lT为隧道计算长度;等式(2)右边为隧道受到的扣件力,具体表达式见翟婉明的研究;Cd和Kd为隧道沿长度方向的分布阻尼和分布刚度,公式见式(3)～式(5)。

(3)

Cd=ξKd

(4)

Ad=adb

(5)

式中:Ed和ξ分别为隧道下卧土层动弹性模量和阻尼比;Ad为盾构隧道管片与地基的等效接触面积;ad为盾构隧道管片与地基的等效接触长度;b为管片宽度;H为地基动荷载压缩层厚度。

旧版HJ 453—2008《环境影响评价技术导则 城市轨道交通》中将地下线振动源强定义为道床上部近轨外侧0.5～1.0 m处的VLZmax,而新版HJ 453—2018《环境影响评价技术导则 城市轨道交通》中将地下线振动源强定义为高于轨顶面(1.25±0.25)m处隧道壁的VLZmax,具体位置见图2。苏浩等[16-17]通过现场实测发现,同一测试断面道床处VLZmax一般高于隧道壁处。因此,为了反映振动从隧道底部至源强测点的传播衰减过程,本文将ad定义为隧道底部至隧道两侧源强测点对应弧长(图2)。

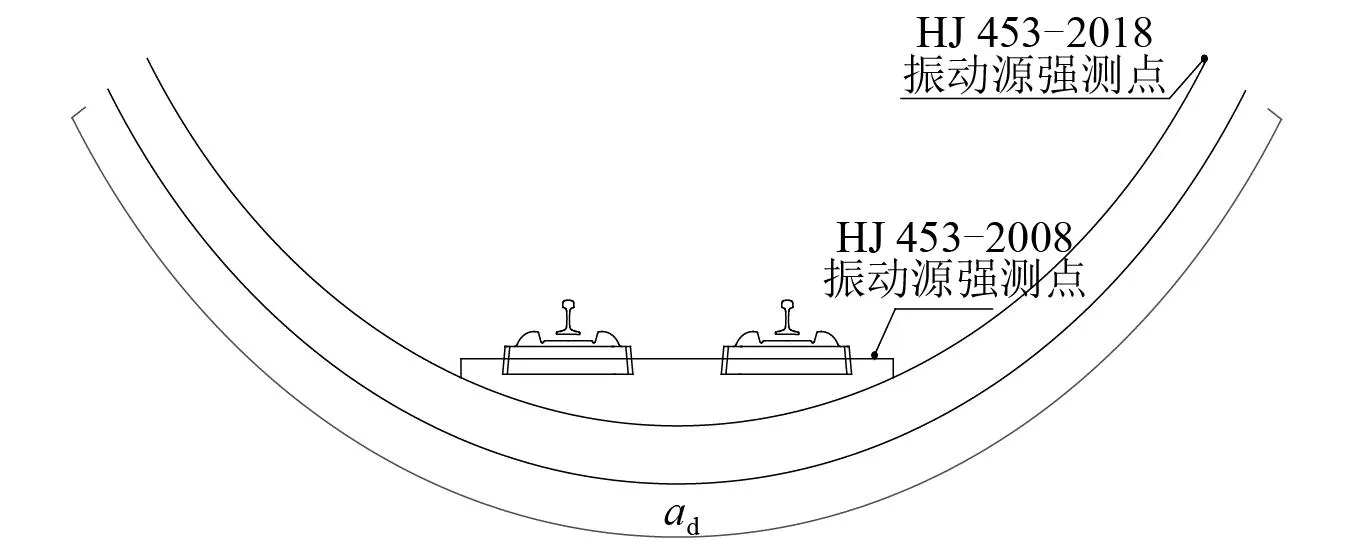
图2 源强测点Fig.2 Vibration source strength test point

1.2 模型验证

源强的随机不确定性主要源于参数的随机不确定性,当所有参数已知时,可以通过确定性模型对断面源强进行准确预测。因此,本文选取广州地铁试运营线路某普通整体道床断面隧道壁实测数据对所建模型进行对比验证。该线路隧道截面形式为圆形,隧道内径8 100 mm,盾构管片厚300 mm,取盾构隧道管片与地基的等效接触长度ad=8.2 m;车辆为空载地铁A型车,具有8节编组,列车运行速度为80 km/h;轨道形式为长枕埋入式;轨道不平顺为断面实测不平顺,扣件为DZ-Ⅲ型扣件。模型验证所用具体参数见表1。

表1 模型验证参数Tab.1 Model validation parameters

该工况在处理器为Intel i9-13900KF的计算机上计算所用时间为90 s,传统有限元数值仿真模型计算时间在2 h左右,相较于有限元模型计算效率提升了近百倍,说明本模型具有极高的计算效率。

该断面隧道壁振动实测数据的采样频率较高,我国现行规范GB/T 13441.2—2008《机械振动与冲击 人体暴露于全身振动的评价 第2部分:建筑物内的振动(1 Hz～80 Hz)》[18]中环境振动主频为1～80 Hz,所以在进行模型验证之前要对实测数据进行滤波处理。

图3(a)给出了隧道壁垂向振动加速度的实测数据与80 Hz低通滤波的结果;图3(b)为实测与仿真在1～80 Hz内的时域结果对比,实测与仿真的振动加速度幅值分别为0.189 m/s2、0.165 m/s2,误差为12%;图3(c)为1～80 Hz内的1/3倍频程计权后结果对比,从图中可以看出,仿真与实测结果重合度较高,源强分别为82.2 dB、81.3 dB,相差0.9 dB。

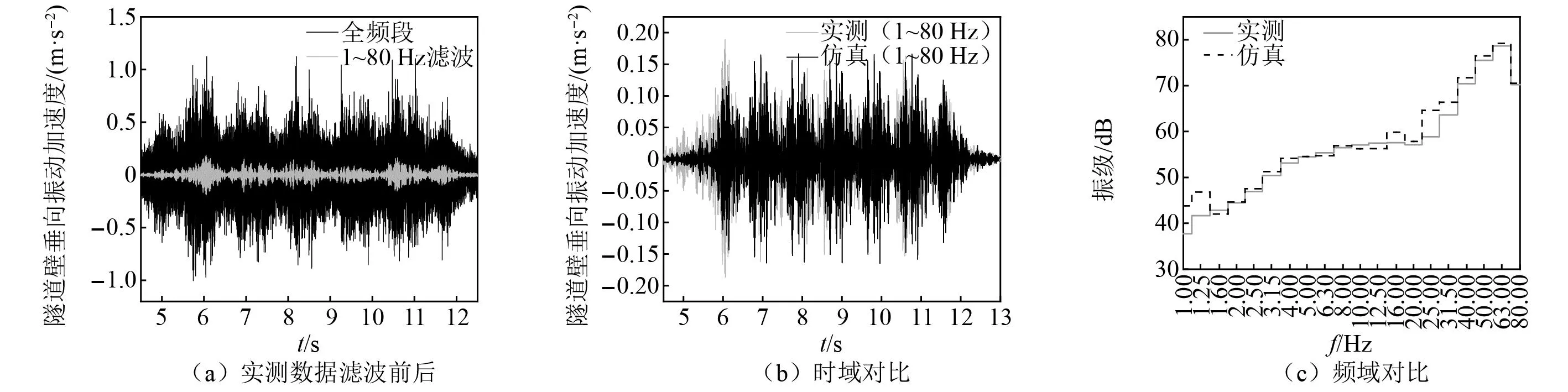
图3 验证结果对比Fig.3 Comparison of verification results

综上所述,可认为本模型具有足够的准确度。

2 随机可靠度分析

在实际工程中,通常难以对所有断面进行实测得到准确的仿真参数,因此,为了提高源强预测的准确度,基于车辆-轨道-盾构隧道耦合振动模型与蒙特卡罗模拟法提出了一种源强预测随机可靠度分析方法,以轴质量和簧下质量修正项CW、轮轨条件修正项CR及隧道型式修正项CT为例,研究了导致其预测准确度具有随机不确定性的主要因素。

2.1 可靠指标

可靠指标β与可靠度之间存在一一对应的关系,工程上一般采用可靠指标β来表示结构的可靠度。GB 50216—2019《铁路工程结构可靠性设计统一标准》中将可靠等级分为三级,一级(二级、三级)可靠工程结构的失效后果为经济损失很大(大、一般),社会和环境影响很严重(严重、一般),本文后续案例三级可靠等级为例进行分析,其可靠度为85%,对应的可靠指标β=1.04,实际工程应用中应根据“一事一议”的原则选择相应的可靠等级进行分析。

2.2 轴质量和簧下质量修正项CW

《18导则》提出,当车辆轴质量和簧下质量与源强车辆给出的轴质量和簧下质量不同时,需要使用修正项CW对源强进行修正,CW计算公式见式(6)。

(6)

式中:w0为参考车辆轴质量;w为预测车辆轴质量;wu0为参考车辆簧下质量;wu为预测车辆簧下质量。

现有研究表明[19],扣件弹性垫板、轨枕垫等轨道高分子弹性元件的刚度具有一定的载频变特性,忽略轨道弹性元件刚度的载频变特性将显著低估车辆载质量对振动源强的影响,并且由于我国相关规范中扣件刚度设计仅关注割线刚度,忽略了高频切线刚度,导致不同厂商生产的同一种扣件弹性垫板之间高频切线刚度存在显著差别,可能导致CW预测结果的准确度具有随机不确定性。

因此,本文选用了两个不同厂商生产的DZ-Ⅲ型扣件对CW进行随机可靠度分析,图4(a)给出了这两种扣件所用弹性垫板的非线性荷载-位移曲线,从图4(a)中可以看出,两种弹性垫板具有相同的割线刚度,但1号弹性垫板具有更强的非线性特征;图4(b)为两种弹性垫板分别在空载和满载预压下高频切线刚度的频变曲线,可以看出,两种弹性垫板的高频切线刚度存在显著差异,1号弹性垫板的高频切线刚度空载时更低,满载时更高。

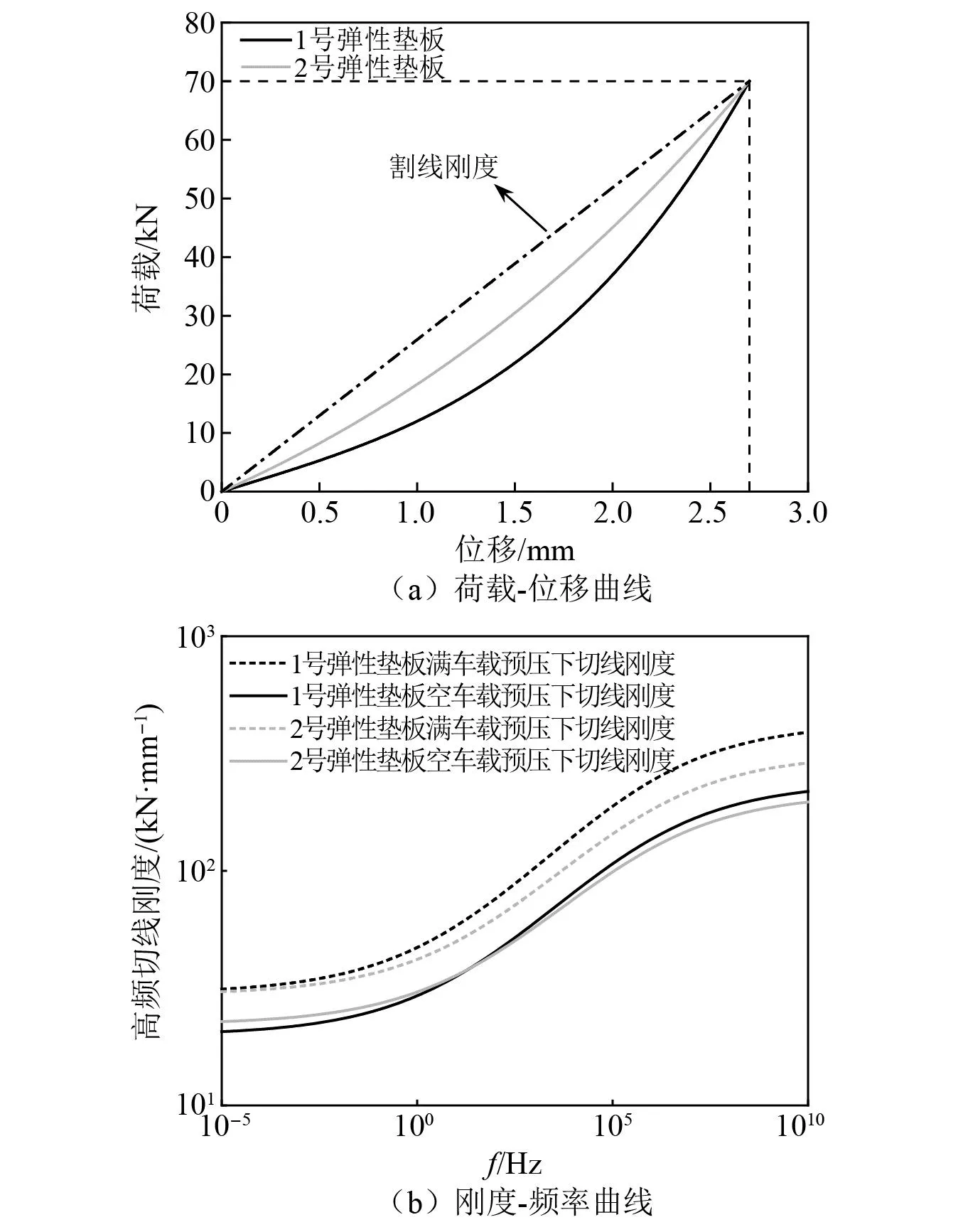
图4 扣件非线性曲线Fig.4 Nonlinear curve of fastener

同一线路一般采用同一种车型,不同车辆之间簧下质量差别较小,因此CW的随机分布特征主要取决于轴质量,而轴质量的随机分布特征取决于线路逐时客流量,且线路逐时客流量在每一周的分布规律类似,本文以文献[20]中对某地铁站一周逐时客流量的实测数据为例(图5)进行分析。假设每小时客流量超过9 000人时列车达到满载状态(轴质量17 t),每小时客流量小于500人时列车为空载状态(轴质量10 t),每5 min有一趟列车通过该站,即可以拟合出了列车轴质量在一周内的分布情况(图6),该线路列车一周内满载仅占总时间的6%,空载占总时间的11.6%。根据式(4)可以算出此时轴质量与簧下质量修正项CW=4.5 dB。

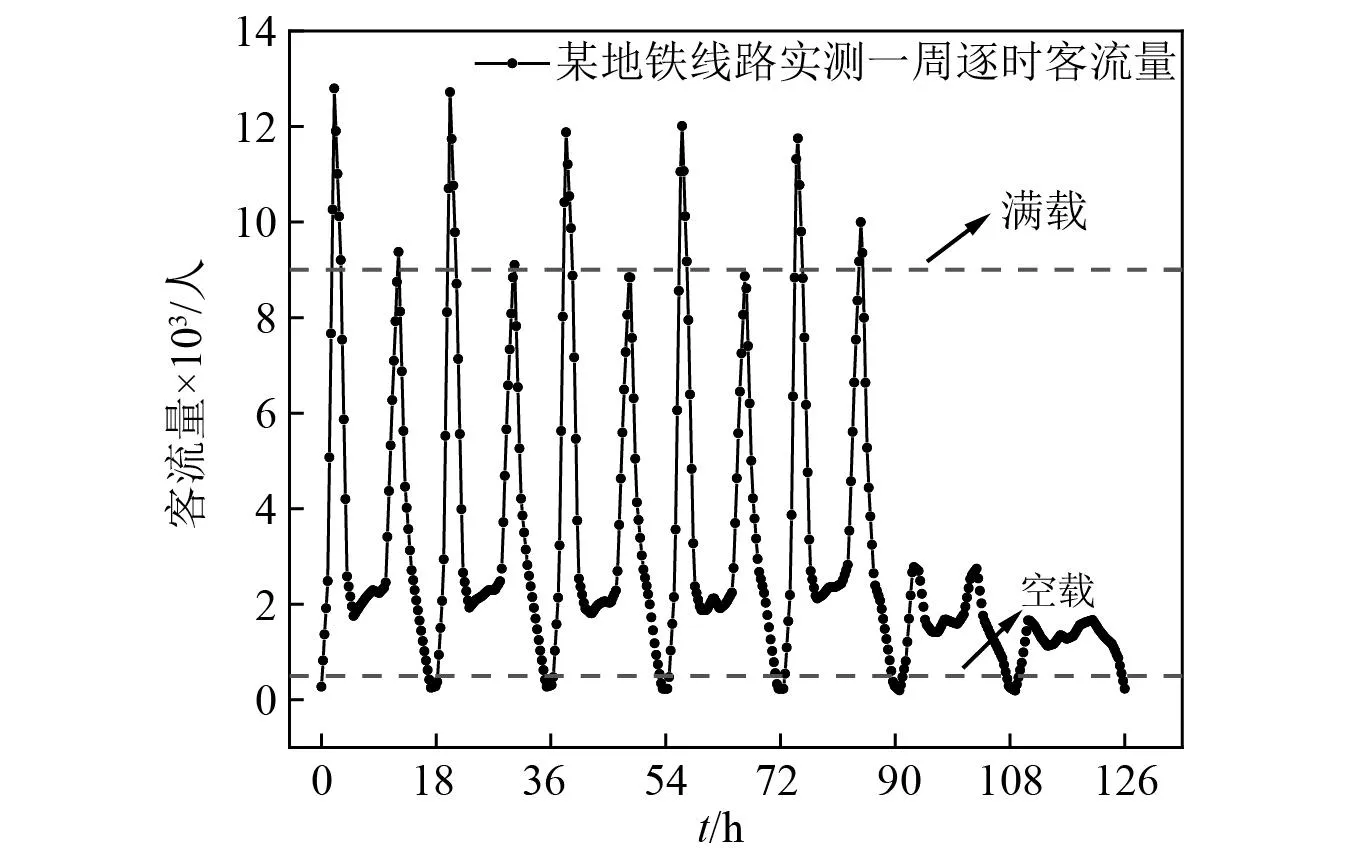
图5 逐时客流量Fig.5 Hourly ridership

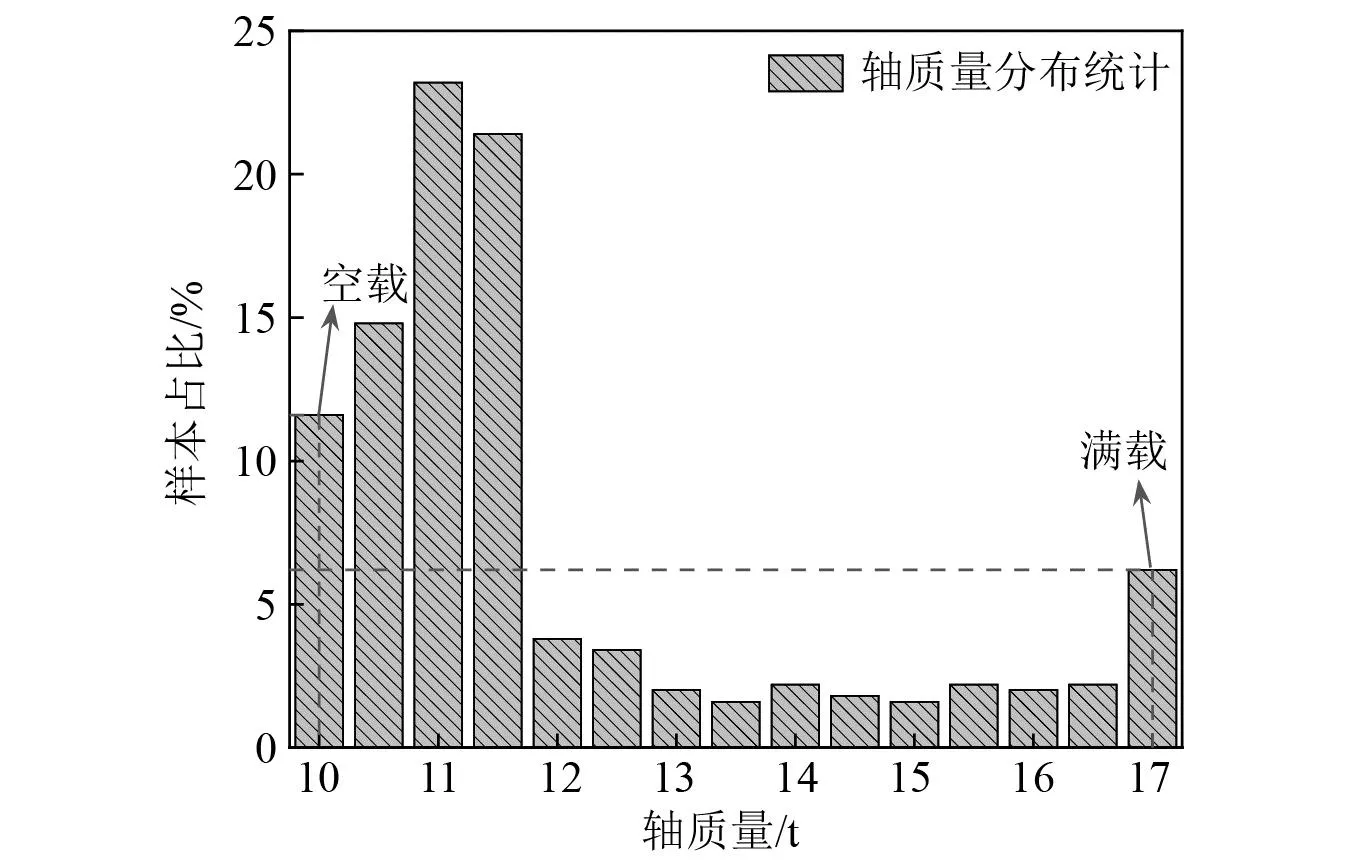
图6 轴质量统计图Fig.6 Axle load statistics

将不同弹性垫板的非线性曲线代入车辆-轨道-盾构隧道振动模型中,以非线性弹簧替换原有的线性弹簧,并将列车轴质量在一周内的统计分布数据换算成车体质量输入模型,其余仿真参数与表1保持一致,即可计算得到一周内不同轴质量下振动源强分布情况。图7给出了空载和满载时隧道壁垂向振动加速度1/3倍频程图和一周内源强的分布情况。

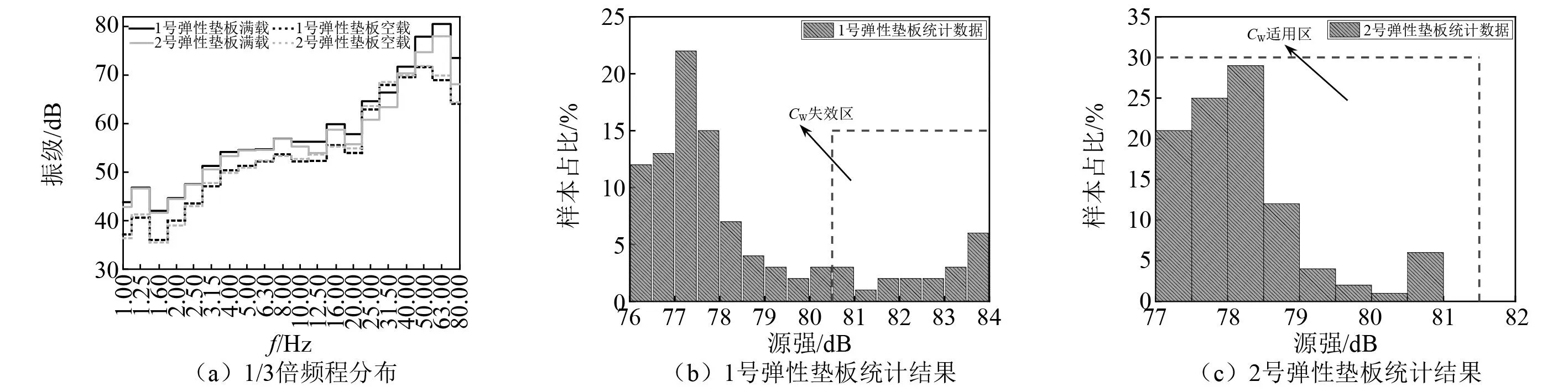
图7 计算结果Fig.7 Calculation result

从图7(a)中可以看出,列车满载状态下隧道壁的振动普遍大于空载状态下。其中1～10 Hz的低频振动主要由准静态荷载引起,且振幅与载荷成正比,差值最大可达6 dB;50～80 Hz的中高频振动主要受扣件高频切线刚度的影响,满载下轮轨一阶固有频率和中高频振动均高于空载,因此满载时的源强将大于空载,差值与扣件弹性垫板刚度载频变曲线的非线性程度有关,1号、2号扣件弹性垫板下满载与空载的源强之差分别为7.9 dB、3.8 dB。

从图7(b)、图7(c)中可以看出,源强在一周内的分布特征为与轴质量分布相关的随机分布。对于一个随机分布的统计样本,轴质量与簧下质量修正项CW可靠指标β的计算公式如式(7)所示

(7)

式中:VLZmax空为空载时的源强;m载质量、σ载质量分别为随机样本的均值和标准差。

1号弹性垫板对应统计样本计算得到可靠指标β=0.83,略小于1.04。说明此时CW不能满足85%可靠度的要求,建议此时CW取5.5 dB;2号弹性垫板对应统计样本计算得到可靠指标β=2.7,远大于1.04,说明此时CW过于保守,按此设计减振轨道可能会增加不必要的经济成本,建议此时CW取2 dB。

2.3 轮轨条件修正项CR

《18导则》提出,当钢轨存在波浪形磨耗时,环境振动源强会明显增大,此时需要利用CR对振动源强进行10 dB的修正。然而,由于我国地铁线路质量管理标准中缺乏短波不平顺管理指标,导致不同线路的钢轨磨耗程度存在巨大差别,可能导致不同线路CR预测结果的准确度具有随机不确定性。

因此,本文选取3个工况进行研究,工况一为参考工况,线路不存在波磨,长波不平顺(1～42 m)选择美国六级谱,短波不平顺(0.1～1.0 m)选择ISO 3095:2013轨道粗糙度谱;其余工况为待预测工况,长波不平顺(1～42 m)也选择美国六级谱,短波不平顺(0.1～1.0 m)根据磨耗程度的不同选择马蒙等[21]基于北京地铁普通整体道床实测数据建立的Q2级和Q4级波磨功率谱。对应的功率谱密度图见图8。

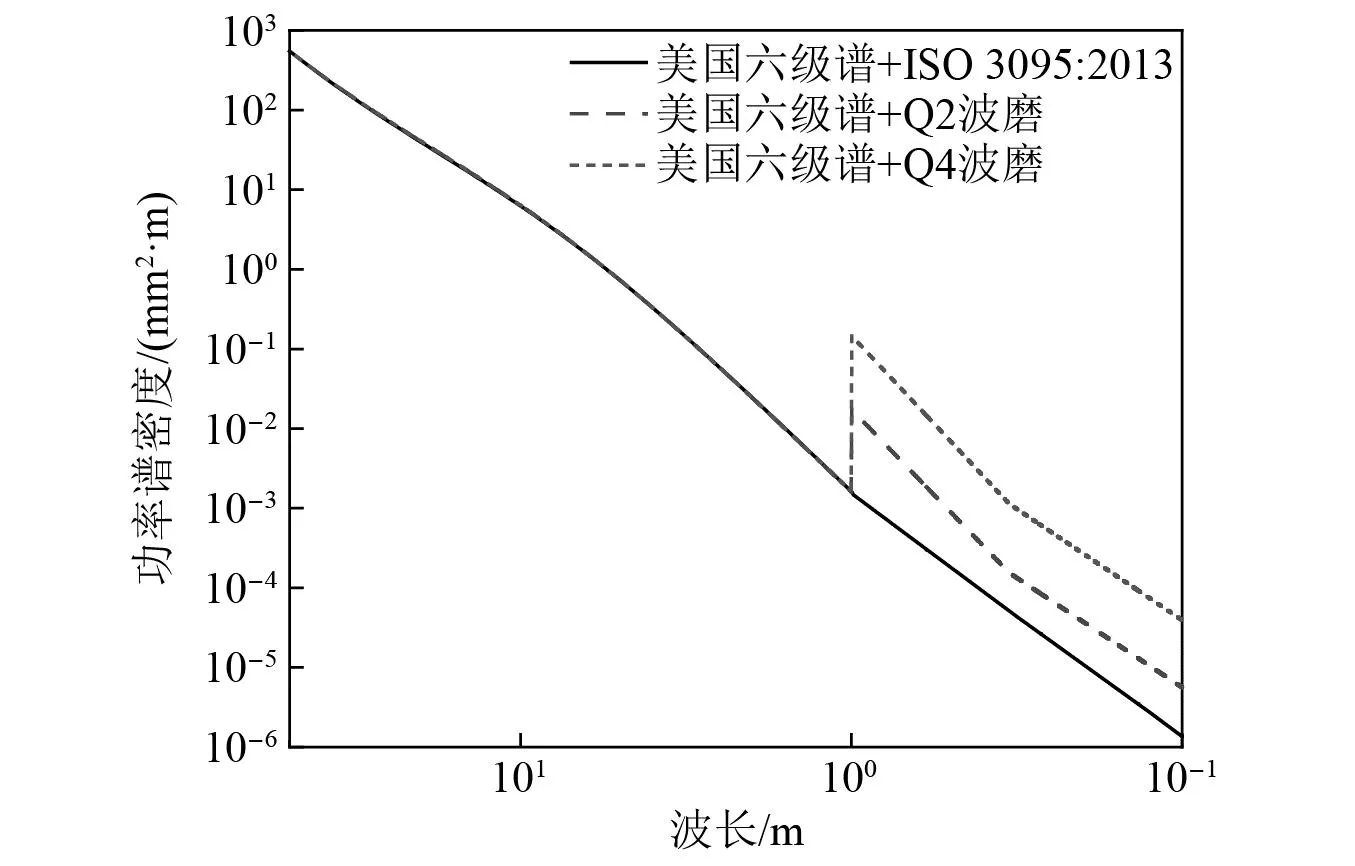
图8 功率谱密度Fig.8 Power spectral density

对轮轨条件修正项CR进行随机可靠度分析时必须考虑轨道不平顺随机不确定性对源强随机分布的影响,因此,以上述谱线分别生成大量随机时域样本作为外部激励输入车辆-轨道-盾构隧道耦合模型,其余仿真参数与表1、表2保持一致,即可得到随机源强均值曲线,如图9所示。从图9中可以看出,在样本数量大于50之后源强均值的波动已经小于0.1%,可以认为样本空间已收敛,为了确保统计样本可靠,本文选取100个统计样本。

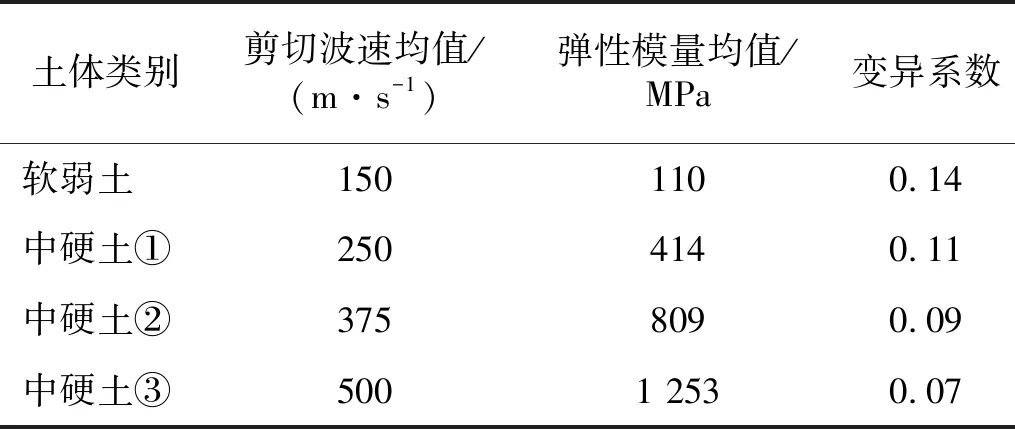
表2 隧道下卧土层随机参数Tab.2 Random parameter of soil layer under tunnel

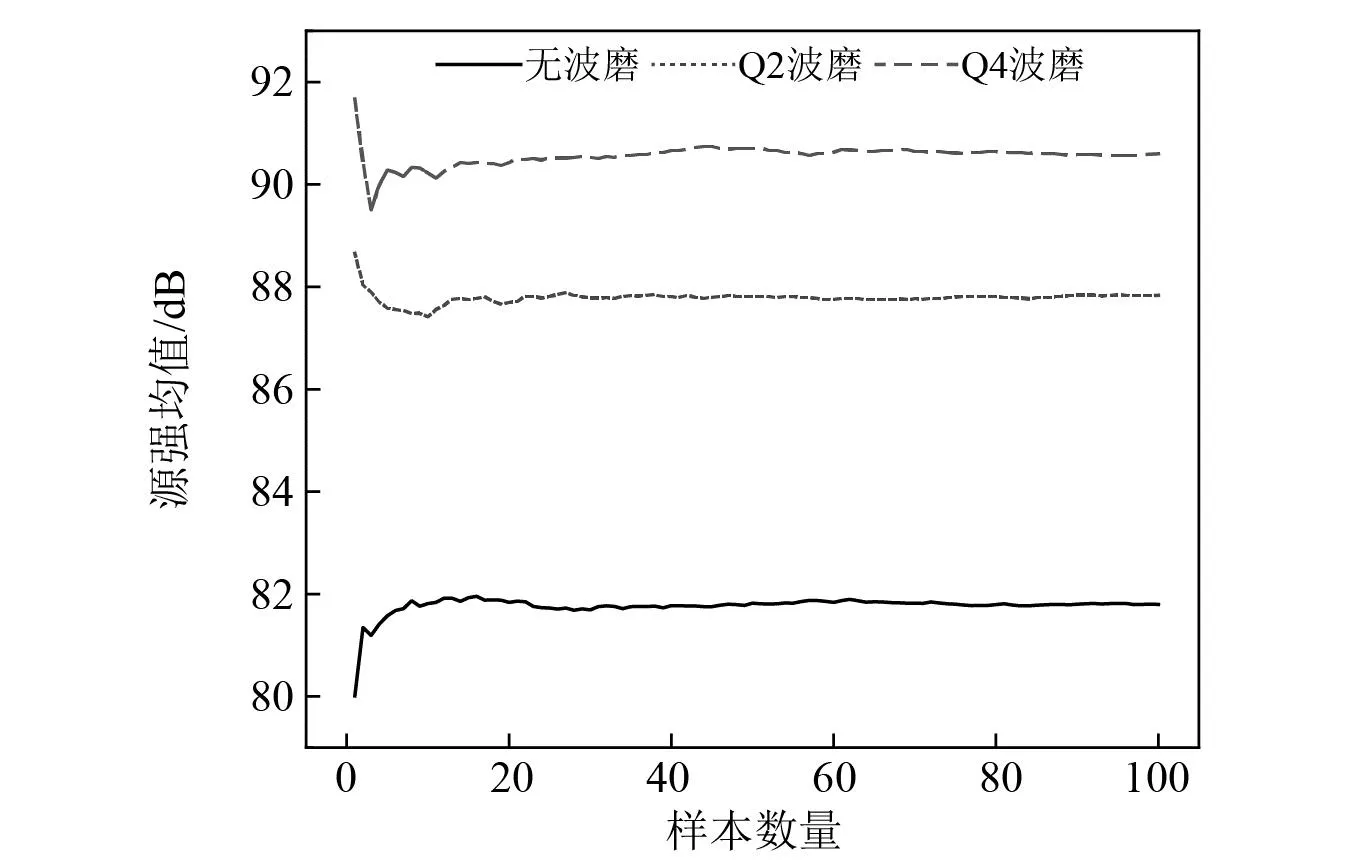
图9 均值曲线Fig.9 Mean value curve

源强随机分布数据统计结果见图10。从图10中可以看出:①轨道不平顺的随机不确定性将会导致同一线路等级不同断面的源强存在6～8 dB的差异,离散性与钢轨磨耗程度成正比;②源强随机分布特征近似呈正态分布,对于两个正态分布的变量,可靠指标的计算公式如式(8)所示

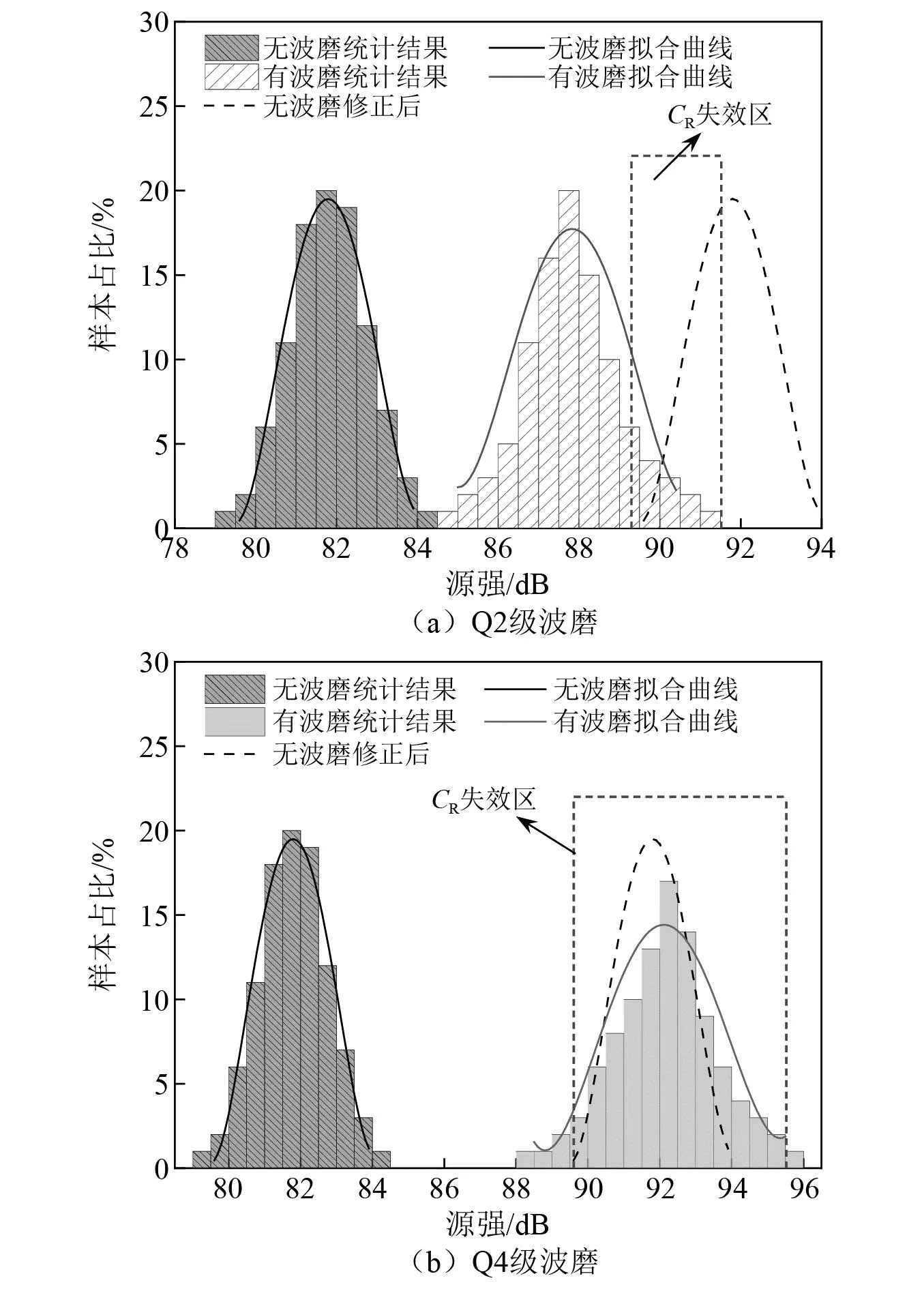
图10 统计结果Fig.10 Statistical result

(8)

式中:m有波磨、σ有波磨分别为有波磨随机源强统计样本均值和标准差;m无波磨、σ无波磨分别为无波磨随机源强统计样本的均值和标准差;

当钢轨磨耗等级为Q2时,轮轨条件修正项CR的可靠指标β为2.44,远大于1.04,说明此时导则预测过于保守,按此设计减振轨道可能会增加额外经济成本,建议此时CR取7.5 dB;当钢轨磨耗等级为Q4时,轮轨条件修正项CR的可靠指标β为0.42,小于1.04,说明此时导则预测失效概率较高,按此设计减振轨道有较大概率导致敏感点振动超限,建议此时CR取13 dB。

2.4 隧道型式修正项CT

《18导则》提出,当隧道下卧土层为中硬土时,需要利用隧道型式修正项CT对振动源强进行6 dB的修正。然而,导则将中硬土定义为剪切波速在250～500 m/s的土体,该范围较大,不同种类中硬土的弹性模量存在较大差别,可能会导致CT预测结果的准确度存在随机不确定性。

土壤的弹性模量具有显著的空间变异性,即使在同一土层之中不同的点上也会有所不同[22],因此,在对CT进行随机可靠度分析时必须考虑隧道下卧土层弹性模量的随机不确定性。本文选取4种土体进行分析,随机参数见表2,其中变异系数基于文献[23]选取。软弱土为对比组,中硬土为待修正组,从表3中可以看出不同中硬土之间弹性模量的差异交大,中硬土①和中硬土③的差值达到了839 MPa。

假设土体弹性模量为符合对数正态分布的随机变量,利用拉丁超立方抽样(Latin hypercube sampling,LHS)法建立能够反映不同土体弹性模量空间变异性特征的数据库,该方法为多维分层抽样方法,对输入概率分布进行分层,从输入分布的每个区间中随机抽取样本,抽样被强制代表每个区间的值,从而避免重复抽样,通过较少的迭代次数准确重建输入分布。

图11为利用LHS法抽样得到软弱土随机样本的弹性模量均值曲线,从图11可以看出,当样本数量大于100时,均值波动已经小于0.1%,可以认为样本空间已收敛,为了确保数据库可靠,本文选取200个随机样本用于仿真分析。将随机样本依次代入车辆-轨道-盾构隧道耦合模型,即可得到考虑隧道下卧土层弹性模量空间变异性的源强统计样本,图12给出了中硬土①计算结果在经过CT修正之后与软弱土统计结果的对比,从图12中可以看出:①隧道下卧土层弹性模量的空间变异性将会导致源强存在7～8 dB的差异;②源强随机分布特征近似呈对数正态分布,对于两个对数正态分布的变量,可靠指标的计算公式见式(9)

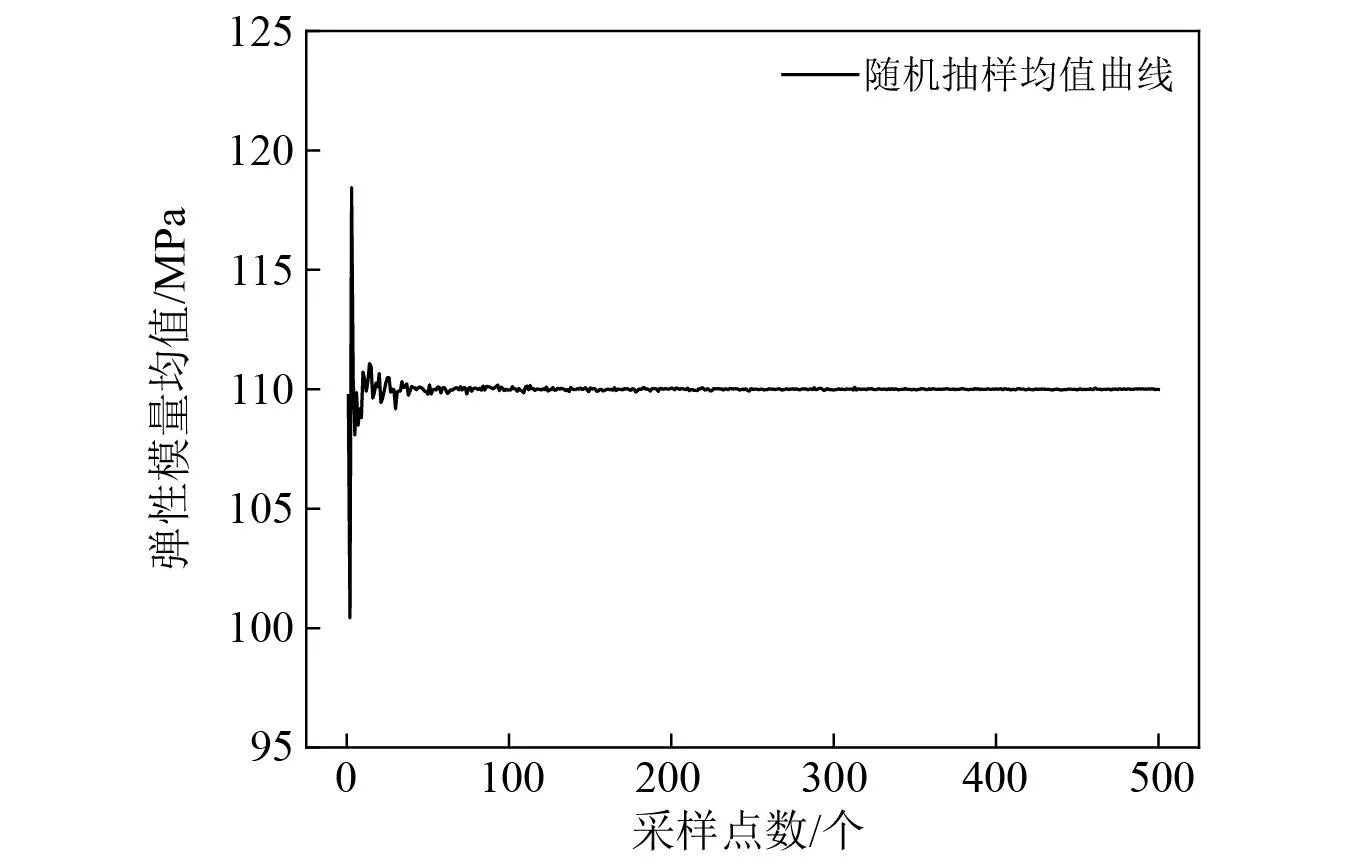
图11 均值曲线Fig.11 Mean value curve

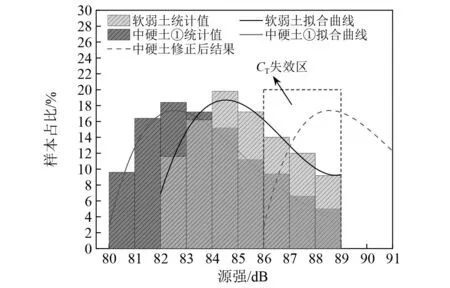
图12 修正对比结果Fig.12 Modified comparison result

(9)

式中:mR、VR分别为中硬土随机源强统计样本经过CT修正后的均值和变异系数;mS、VS分别为软弱土随机源强统计样本的均值和变异系数。

图13给出了不同中硬土CT的可靠指标,并拟合出了可靠指标与剪切波速的关系曲线,从图13中可以看出,可靠指标随着土体剪切波速的增大而减小,当剪切波速在250～375 m/s时,CT的可靠指标接近1.04,此时CT的准确度较高;当剪切波速在375～500 m/s时,CT的可靠指标接近0.85,小于1.04,说明此时CT的准确度较低,按此设计减振轨道有较大概率导致敏感点振动超限,建议此时CT取9 dB。

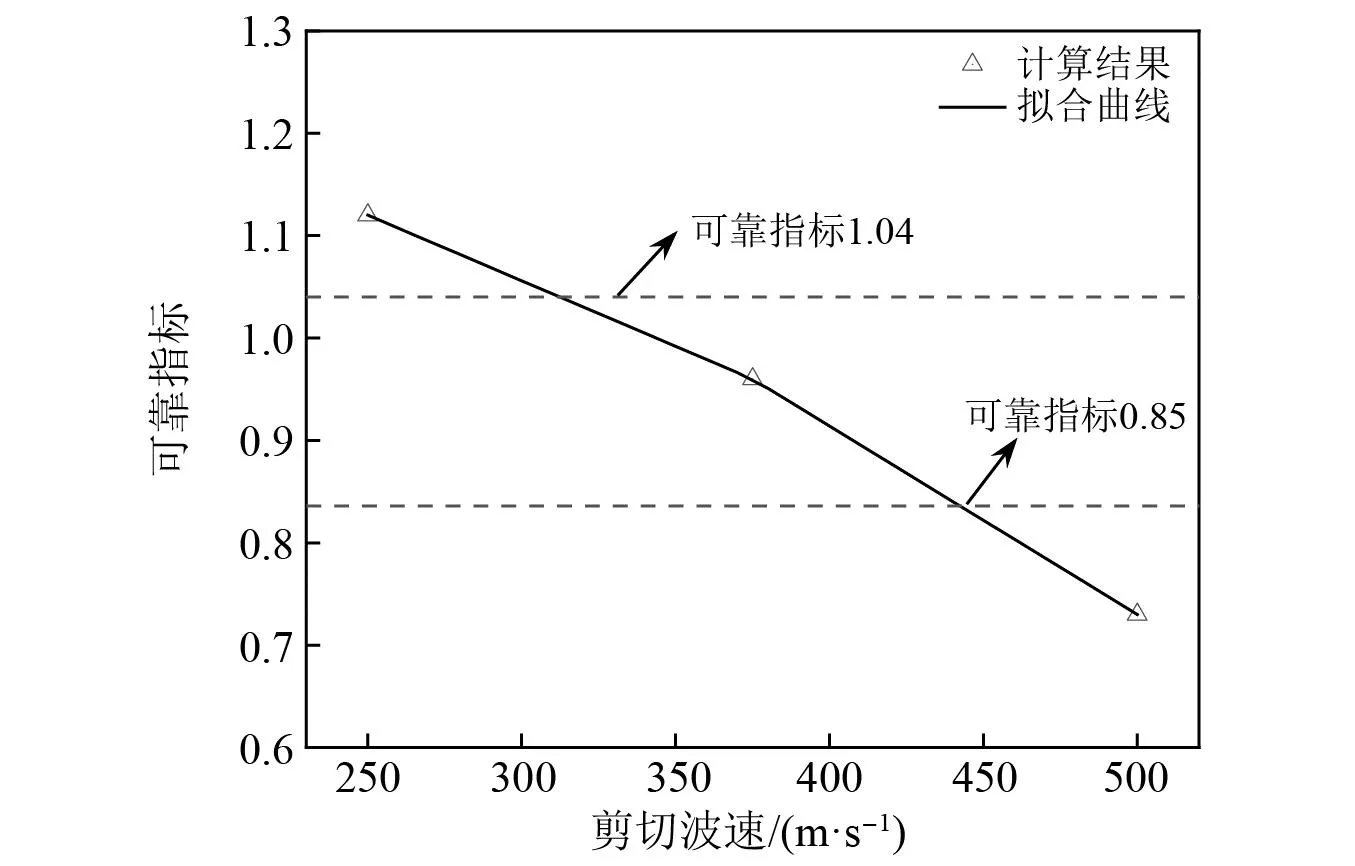
图13 计算结果Fig.13 Calculation result

3 结 论

本文将隧道简化为有阻尼弹性地基上的无限长欧拉梁,将土体等效线性弹簧时考虑了隧道底部至源强测点的传播衰减过程,建立了可以直接反映隧道壁振动水平的车辆-轨道-盾构隧道耦合振动模型,基于MC法提出了一种源强预测随机可靠度分析方法,以轴质量和簧下质量修正项CW、轮轨条件修正项CR及隧道型式修正项CT为例,以85%为目标可靠度研究了其在不同运营条件下预测结果的准确度,分析了导致修正项准确度具有随机不确定性的主要因素。得到的结论与建议如下:

(1)本文建立的车辆-轨道-隧道耦合模型具有较高的计算效率,单个工况计算时间为90 s,可极大地弥补MC法耗时的缺点;隧道壁垂向加速度时域幅值与实测数据误差在12%以内,源强误差在1 dB以内,具有较高的计算精度。

(2)同种扣件不同弹性垫板之间非线性载频变刚度的差异是导致轴质量和簧下质量修正项CW准确度具有随机不确定性的一个重要原因,当目标可靠度为85%时,该因素会导致源强预测存在-1～+3 dB的误差。

(3)不同线路之间钢轨磨耗等级的差异是导致轮轨条件修正项CR准确度具有随机不确定性的一个重要原因。当目标可靠度为85%时,该因素会导致源强预测存在-3～+3 dB的误差。

(4)不同中硬土之间弹性模量的差异过大是导致隧道型式修正项CT准确度具有随机不确定性的一个重要原因。当目标可靠度为85%时,剪切波速在250～375 m/s时,CT的准确度较高;当剪切波速在375～500 m/s时,CT的准确度较低,预测源强误差可达3 dB。

DB11/ T 838—2019《地铁噪声与振动控制规范》根据插入损失将减振措施分为四级,分别是初级减振措施(3～7 dB)、中级减振措施(7～11 dB)、高级减振措施(11～16 dB)及特殊减振措施(>16 dB)。当经验修正项预测准确度存在较大随机不确定性时,会导致源强预测结果存在较大的误差。目标可靠度为85%时,同时考虑CW、CR及CT3个修正项的随机不确定性会使源强预测值出现-4～+9 dB的误差,假设一个敏感点断面实际需要中级减振措施,预测结果偏小4 dB会导致设计施工时仅采取初级减振措施,达不到敏感点的减振要求从而进行线路改造进而造成大量成本浪费;预测结果偏大9 dB会导致设计施工时采取高级甚至特殊减振措施,导致减振能力过剩从而造成大量成本浪费。因此,为了提高《18导则》源强预测的准确度,节约减振成本。建议线路严格控制扣件非线性载频变刚度、钢轨磨耗等级等因素的随机不确定性,同时细化中硬土剪切波速划分范围并提出相应的修正项。