场地均质性对浅埋地铁车站地下结构地震易损性的影响

蒋家卫, 李文彪, 赵雅芝, 陈国兴, 杜修力

(1. 南京工业大学 岩土工程研究所,南京 211816;2. 北京工业大学 城市与工程安全减灾教育部重点实验室,北京 100124)

城市地铁作为现代交通系统的骨干,对提升城市公共交通运行效率、缓解交通拥堵、引导优化城市空间结构布局、改善城市环境起到了重要作用。然而,1995年日本阪神地震导致了神户市内城轨系统中大开站、长田站、三宫站、上泽站以及一些区间隧道发生了不同程度的破坏[1]。其中,尤以大开地铁车站破坏最为严重,是迄今为止唯一发生完全坍塌的大型断面地下结构,造成了重大的经济损失,并给灾后的重建修复工作带来了巨大的挑战。因此,基于性能的抗震设计理念[2],对已建或正在建设的地铁车站结构进行地震风险评估尤为重要。

作为基于性能的抗震设计框架的重要组成部分之一,地震易损性分析旨在评估结构在不同水平地震动强度作用下超越特定性能水准的破坏概率。随着人们对地下结构抗震安全问题的重视,近年来,地震工程学者基于数值分析方法对地下隧道[3-5]、管廊[6-7]、地铁车站[8-11]等地下结构开展了众多地震易损性方面的研究,并得到了一些有意义的结果。例如,Zhong等基于增量动力分析(increment dynamic analysis,IDA)方法对大开地铁车站进行了地震易损性分析,其结果与大开地铁车站实际发生破坏现象相吻合。Jiang等研究了不同特性地震动记录集对地铁车站地下结构的地震易损性分析结果的影响。Huang等[12]基于数值方法建立了上海市层层场地条件下某区间隧道的地震易损性曲线。然而,目前鲜有关于场地条件对地下结构地震易损性的影响。相关研究表明[13-15],土-结构相互作用是影响地下结构地震响应关键因素,受周围土层约束,地下结构地震响应主要由场地非线性动力响应所决定。因此,开展场地特性对地铁车站结构地震易损性分析对地下结构基于性能的抗震设计具有重要意义。

本文以北京某两层两跨地铁车站结构为研究对象,基于数值分析方法开展均质场地与层层场地下车站结构的地震易损性分析,旨在给出场地均质性对地下结构地震易损性分析结果的影响,为地下结构基于性能的抗震设计提供科学参考。

1 基于增量动力分析方法的地震易损性分析

地震易损性分析工作主要包含两个模块:结构的概率地震需求模型与结构损伤模型。其中概率地震需求模型主要求解结构在相应水平地震动强度作用下结构的均值响应与标准差;而结构损伤模型给出结构的破坏等级划分以及相应的性能指标。

1.1 增量动力分析方法

基于IDA[16]方法建立结构的概率地震需求模型是目前地震易损性分析最常用的数值分析方法。IDA方法的核心是通过对原始地震动记录进行调幅,然后输入模型进行非线性动力响应分析,以获取结构从弹性至弹塑性状态的全反应过程,鉴于IDA方法已经被广泛应用于当前地下结构的地震易损性分析研究中[17],这里仅对几个关键变量进行阐述。

为基于IDA方法所得到的IDA曲线簇,如图1所示,通过IDA曲线簇可分别绘制16%分位线、50%分位线、84%分位线。可假设结构响应与地震动强度参数之间服从自然对数正态分布,因此,可取IDA(记AID)的50%分位线为结构的响应均值(Sd),而其标准差可通过式(1)计算得到

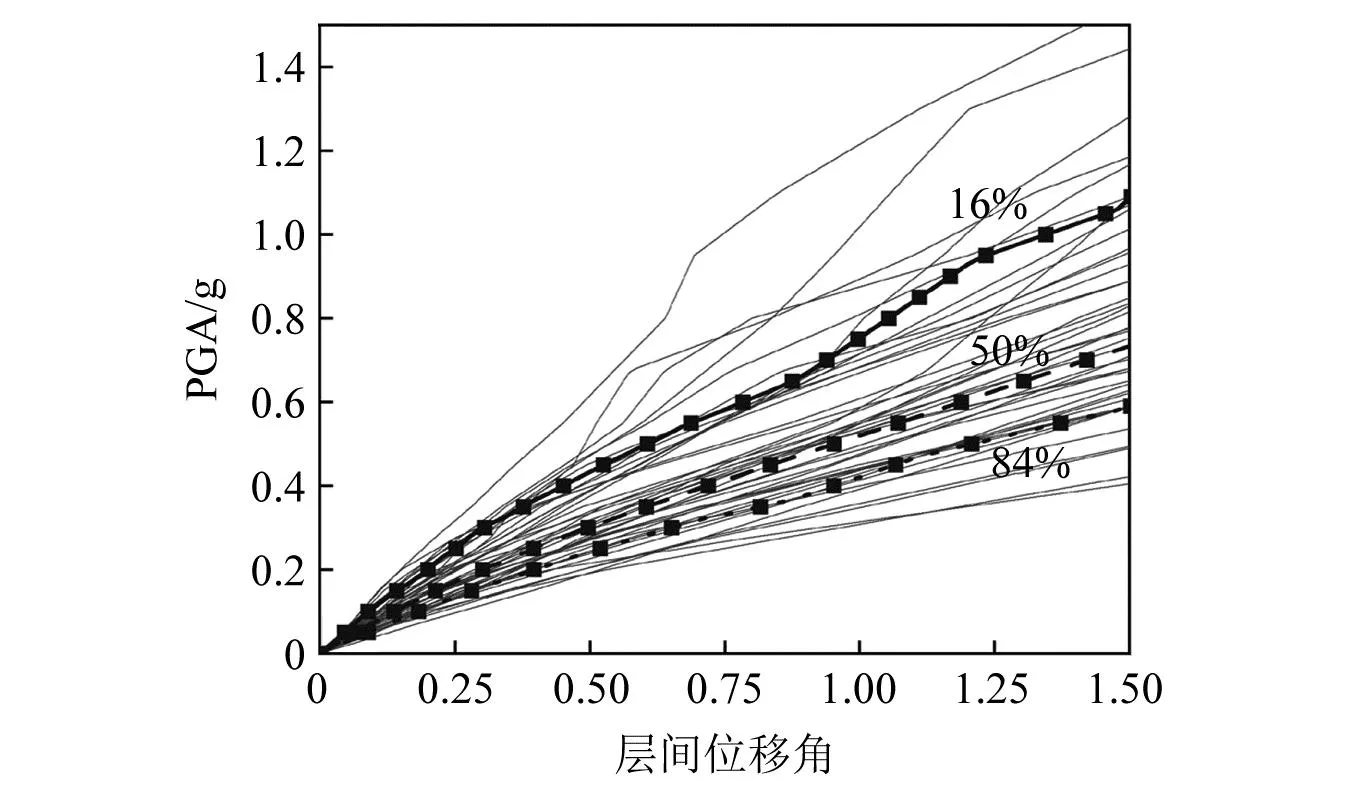
图1 IDA曲线簇Fig.1 IDA curves cluster

(1)

1.2 地铁车站结构抗震性能指标

根据美国FEMA-P58报告的建议,采用单一的损伤参数来描述结构的全局破坏状态是当前评估结构抗震性能的重要手段之一。基于大开地铁车站的地震破坏机理研究表明[18],中柱是车站结构抗震最为薄弱构件,且其抗震性能与其水平变形能力密切相关。鉴于此,杜修力等[19-20]将地铁车站结构划分为四个性能水准,并以层间位移角(interstory displacement angle,IDR)为损伤参数建立了地下地铁车站结构的抗震性能指标体系,即结构超越不同性能水准的损伤限值(SC)如表1所示。

表1 矩形框架地铁地下结构性能水准定义Tab.1 Definition of structural performance level of shallow rectangular subway station

1.3 地震易损性函数

在建立结构概率地震需求模型与定义结构抗震性能指标的基础上,根据FEMA-P695 报告[21],可根据式(2)函数模型建立结构的地震易损性曲线

(2)

式中:φ为标准正态分布函数;SC为结构承载力限值;SD为地震响应均值;βRTR由地震动记录所引起的不确定性;βC结构承载能力或建设质量的不确定性;βMDL分析模型的不确定性。

2 数值模型

2.1 工程背景

本文以北京某铁工程为研究背景。如图2所示,地铁车站横断面为典型的两层两跨矩形框架形式,车站长×高:19.70 m×13.41 m,顶板厚度为0.9 m,底板厚度为0.8 m,中板厚0.4 m,侧墙为0.7 m,中柱截面尺寸为0.7 m×1.2 m。结构为钢筋混凝土结构,主体混凝土强度为C40,中柱为C50,钢筋型号为HRB335。结构顶板埋深3 m,周围土层主要由砂土、黏土、粉土等组成,详见表2,岩土动力学参数如图3所示。为对比研究层层场地与均匀一致场地下地铁车站地震易损性曲线,即两者场地在模型深度方向上表现出不同的均匀性,假定两场地的剪切波速一致,均为300 m/s。

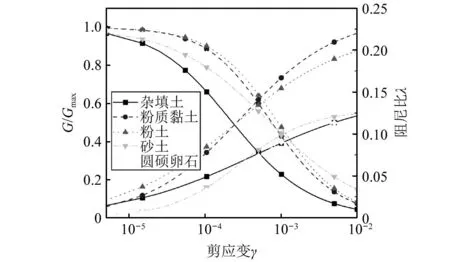
图 3 场地岩土力学特性Fig.3 Geotechnical characteristics of the site

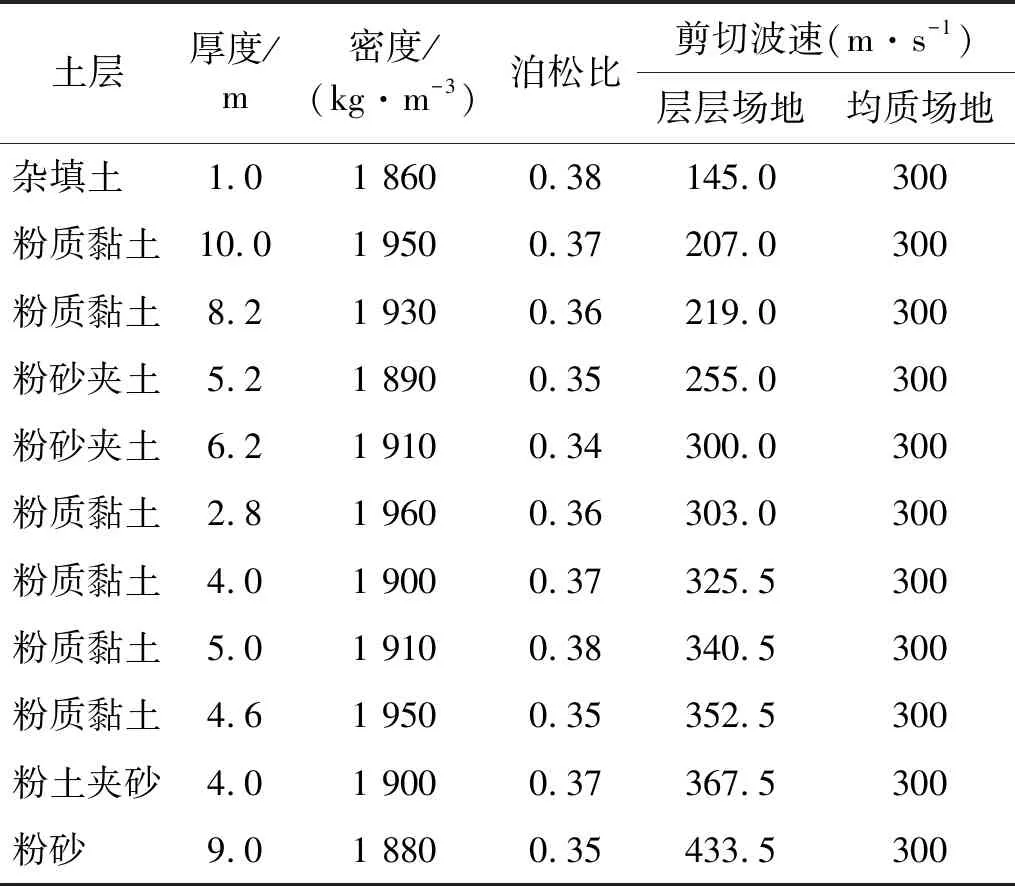
表2 土层参数信息Tab.2 Inhomogeneous soil parameter information

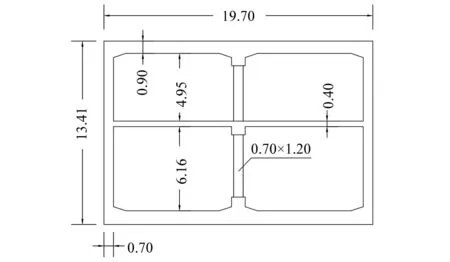
图2 典型车站断面尺寸信息(m)Fig.2 The dimension information of typical subway station cross-section (m)

2.2 数值模型

以层层场地模型为例,如图4所示,基于ABAQUS软件平台建立了考虑土-结构相互作用的数值分析模型,模型边界至结构侧边距离为结构的3.5倍,高度取至基岩面,即60 m。为考虑土体在地震荷载作用下的非线性,选用二维实体单元模拟,其力学特性采用改进的Davidenkov骨架曲线的Non-Masing本构模型进行模拟[22-23],表达式如下

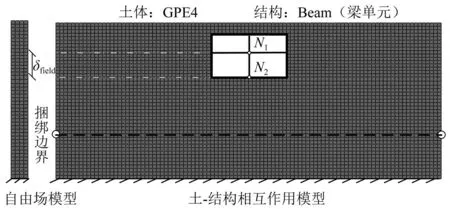
图4 有限元分析模型示意图Fig.4 The diagram of the finite element analysis model

(3)

式中:τ(γ)为剪应力;G与Gmax分别为剪切模量与最大剪切模量;γ为剪应变。值得注意的是改进后的γ0与常数a、b一样,不再具有物理意义,仅作为土性的拟合参数。

结构采用梁单元进行模拟,采用弹塑性损伤本构描述混凝土结构在地震动荷载作用下的受拉-压力学行为[24-25]。通过关键字*Rebar建立钢筋模型,并采用理想弹塑性本构[26]模拟其力学行为。为考虑土体与结构之间的动力相互作用,结构与土体接触面的径向采用硬接触,切向采用摩擦接触,其摩擦因数取0.4,这种假设已被广泛应用于地下结构地震数值分析方法的研究[27]。

由于需要考虑初始地应力,本文数值模拟过程分为两步:第一步,重力荷载,设置模型底部固定,两侧边界仅放开竖向的自由度,完成重力荷载的分析后,提取边界支反力;第二步,输入地震动荷载,在第一步分析的基础上,将模型两侧边界设置为捆绑边界,即对同一高度的侧边节点进行运动耦合约束;导入第一步重力计算结果的支反力与地应力,完成模型的地应力平衡。由于模型底部边界已经延伸至基岩面,本文采用振动法输入地震动荷载。分析过程中监测结构下层中柱节点N1与N2(如图4所示)的位移时程曲线。

2.3 地震动记录

参考FEMA-P695报告,选取22组远场地震动记录作为结构进行地震易损性分析的输入地震动记录集,详情如表3所示。

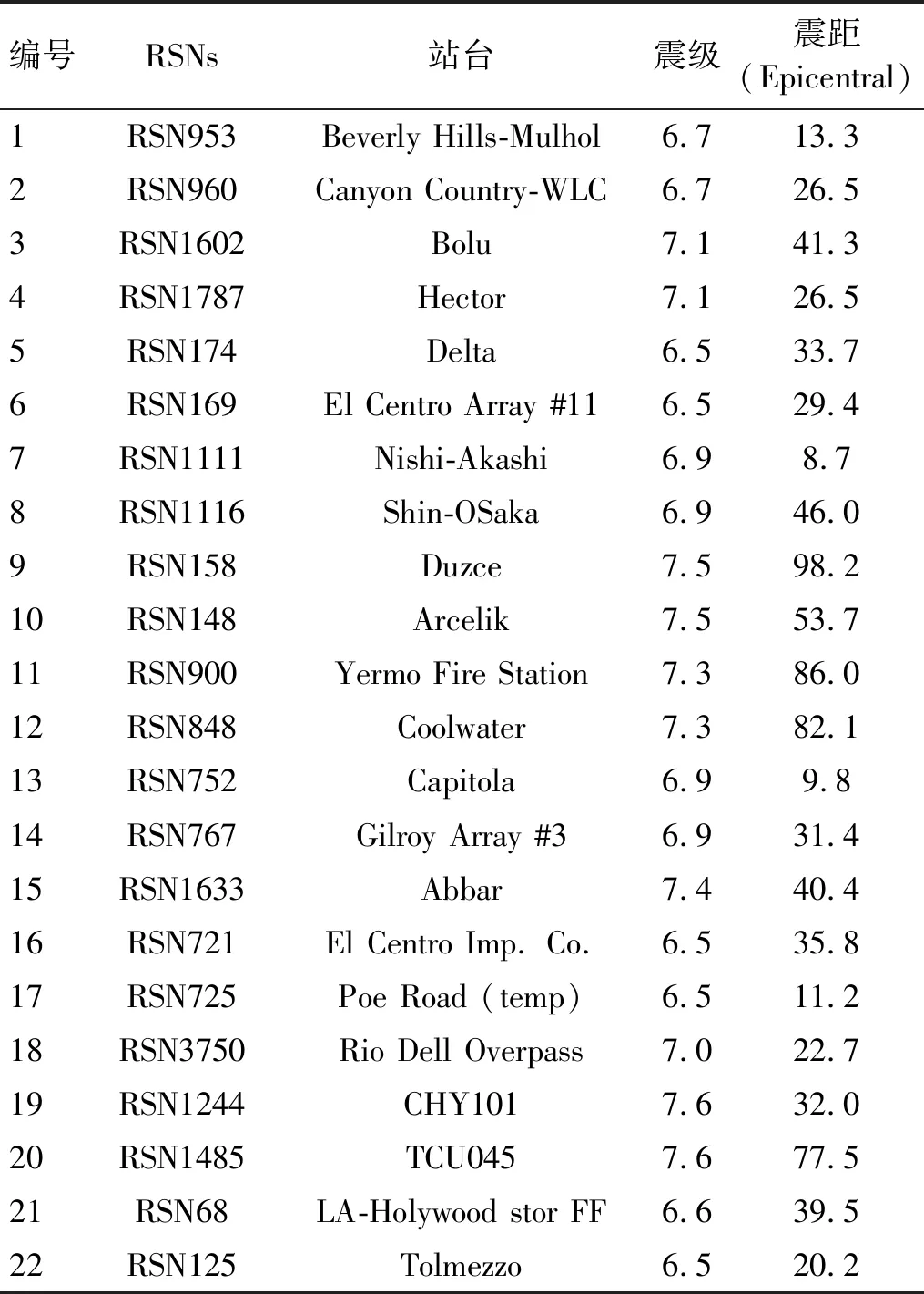
表3 地震动记录信息Tab.3 The ground motion record information

3 分析结果

蒋家卫等[28]针对浅埋地铁车站框架结构,提出了以峰值地面加速度(peak ground acceleration,PGA)为最优地震动强度指标。如图5所示,为基于层间位移角与PGA两参数所绘制的IDA曲线簇,由图5可知,地下结构IDA曲线簇与地上结构IDA曲线具有显著差异,由于受到周围土体的约束,地下结构IDA曲线基本呈现单调递增趋势,这与地上结构IDA曲线会出现明显的“硬化段”所不同,该现象也在其他地下结构基于IDA方法的地震易损性研究中所报道。

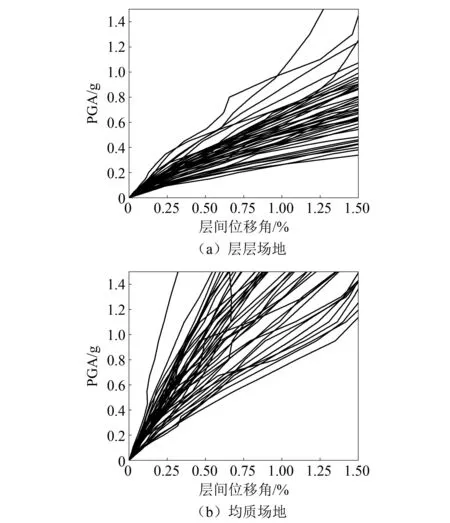
图5 基于不同场地计算所得到的地铁车站IDA曲线簇Fig.5 The IDA curves cluster computed based on different site conditions

如图6所示,基于所得到的IDA曲线簇,计算得到相应的IDA分位线。根据Cornell等研究,可以假设结构的地震反应与地震动强度参数之间服从对数正态分布,因此,其中50%分位线代表了结构在一定水平地震动强度作用下的响应均值,对比层层场地与均质场地条件下50%分位线可知,在相同水平地震动强度激励下,层层场地条件下结构的地震响应均值要明显大于均质场地。

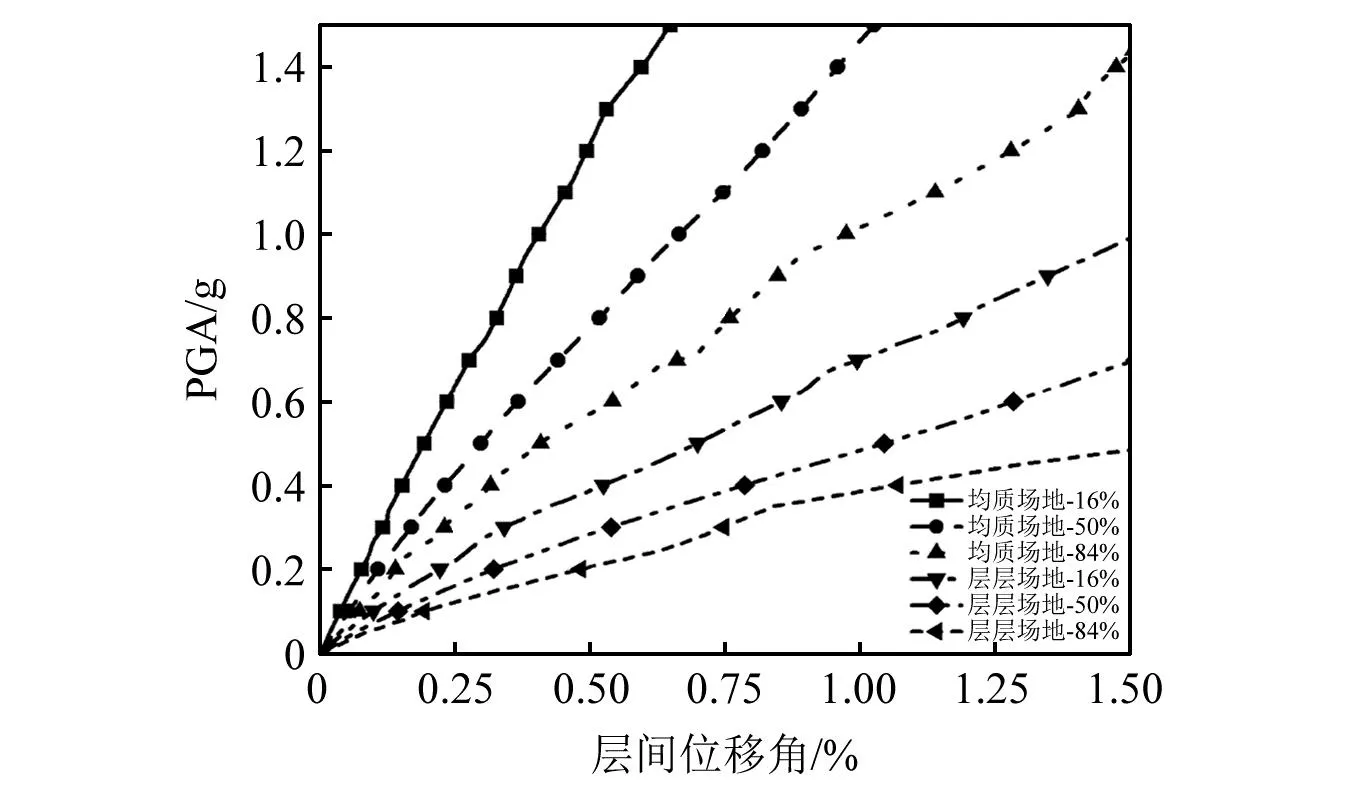
图6 基于IDA曲线计算的分位线Fig.6 The percentile lines computed from IDA curves

进一步基于16%与84%分位线计算结构层间位移角响应标准差,如图7所示。由图7可知,两种场地条件下结构的响应标准差并无明显差距,这可以解释为结构响应的离散程度主要由输入地震动记录所决定。综上所述,场地条件的差异性对于结构的响应均值影响显著,但对于反应参数的标准差影响较小,处于均匀场地中结构的反应标准差一般小于层层场地,这可能是由于地震波在均匀场地与层层场地中传播规律不同所引起,显然层层场地会带来更大的不确定性。

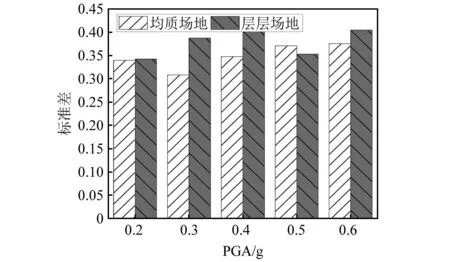
图7 结构层间位移角标准差Fig.7 The standard deviation of IDR of structure

根据地震易损性函数式(2),分别计算得到结构在不同场地条件的地震易损性曲线,如图8所示。由图8可知,基于层层场地计算得到的地震易损性曲线(图中虚线)均位于均质场地地震易损性曲线(实线)上方,由此说明,结构在层层场地条件下的地震响应超越相应性能水准限值的概率更高。例如,当所输入地震动强度PGA=0.2g时,结构在层层场地条件下超越性能等级1的概率为98%,在均质场地条件下超越性能等级1的概率为72%,两种场地条件下结构超越性能等级2的概率分别为58%与3%。当所输入地震动强度PGA=0.4g时,结构在层层场地条件下超越性能等级2的概率为97%,而在均质场地条件下超越性能等级2的概率仅为33%,进一步,在层层场地条件下,结构超越性能等级4的概率为34%,而在均质场地中其超越概率仅为1%。以上数据表明,场地的均质性对地下结构的地震易损性分析结果具有显著影响,结构处于层层场地条件下的破坏概率要明显高于其在均质场地。

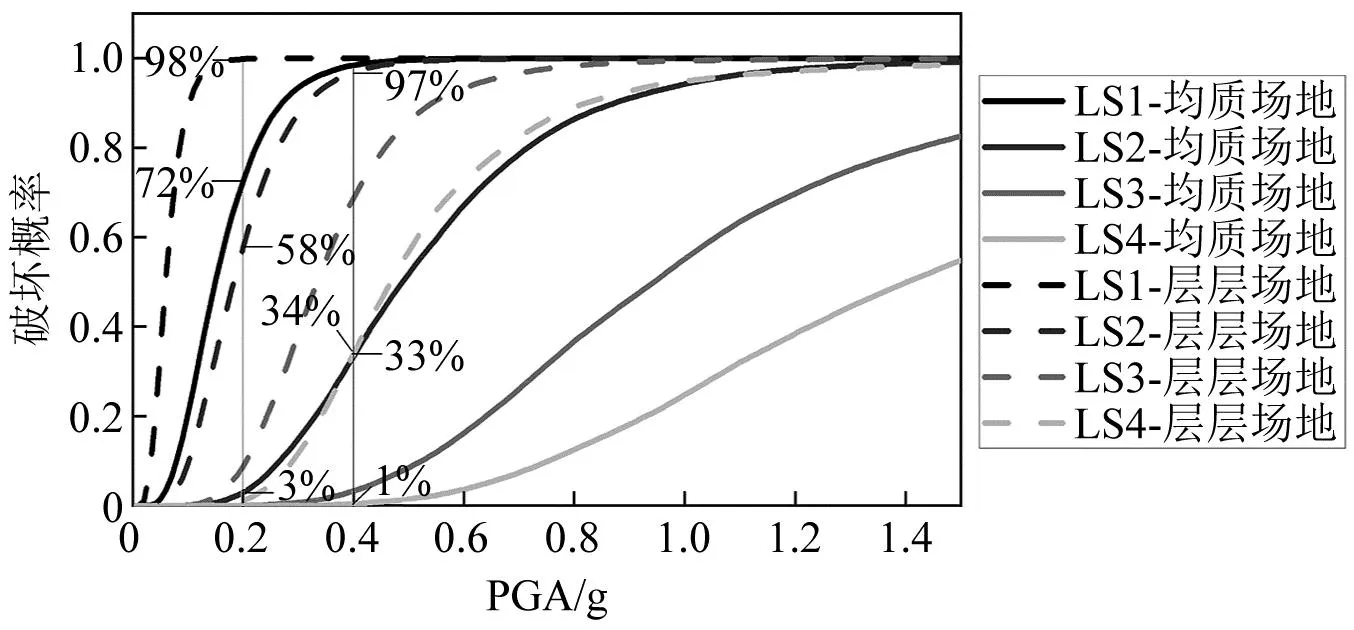
图8 地铁车站地下结构地震易损性曲线Fig.8 The seismic fragility curves of subway station underground structure

分析认为,由于地下结构的变形主要受周围土层所约束,因此,地下结构的层间位移响应必然与相应位置土层的层间变形相关,由此,推断层层场地中毗邻结构土层(与结构等高度的土层)的响应相对值(定义为δfield,见图4)必然大于均质场地。为进一步证实上述分析,分别提取两种场地条件下结构高度处土层的δfield。两种场地条件下自由场响应——δfield均值的对比图,如图9所示。由图9可知,结构处于层层场地条件下,其δfield值要明显大于均质场地,这一现象与上述分析一致。同时,相关地下结构地震响应规律研究成果[29]也表明,结构的破坏程度与周边土层的剪切变形密切相关。

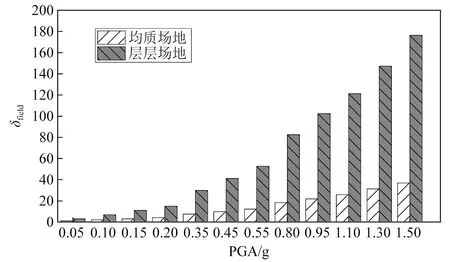
图9 自由场响应的δfield均值Fig.9 The mean of the δfield of free field response

综上所述,可以推断,即使结构所处场地的剪切波速一致,但场地的均匀性对结构的地震破坏概率具有重大影响,处于层层场地的地下结构将面临更大的地震威胁,尤其是结构周边土层的均质性对其影响最为显著。

4 结 论

针对当前缺乏关于场地均质性对地下结构地震易损性的影响研究。本文以北京某两层两跨地铁车站结构横断面为研究对象,基于ABAQUS软件建立了考虑土-结构相互作用的二维有限元分析模型。模型考虑了土体在地震动荷载作用下的非线性力学行为,并考虑钢筋混凝土结构在动力荷载作用的弹塑性变形。采用IDA方法,建立了层层场地与均质场地条件下地铁车站结构的地震易损性曲线。

地下结构IDA曲线簇与地上结构具有显著差异,受周围土体约束,并不会出现显著的硬化段。基于层层场地条件计算所得到的地铁车站结构层间位移角响应均值要明显大于均质场地,但两者所得到的层间位移角标准差基本相同。这表明场地条件对结构地震响应均值影响较大,而对由地震动记录所引起的不确定性影响较小。在相同水平强度地震动记录激励下,即使两种场地的平均剪切波速一致,结构处于层层场地条件的破坏概率要明显高于均质场地。进一步的分析结果表明,这一现象主要由于层层场地中毗邻结构土体具有较大的剪切变形,从而导致结构顶底板发生较大的剪切变形。