基于混合正则化方法的结构载荷识别与响应重构
彭珍瑞, 周雪文
(兰州交通大学 机电工程学院,兰州 730070)
结构健康监测(structural health monitoring, SHM)广泛应用于土木和机械工程领域,大量高层建筑、大跨度桥梁和大型空间结构等都安装了SHM系统,实时监测和评估结构的服役状态。准确获取结构外部载荷和各类型响应数据对其可靠性分析、动态优化设计及健康监测至关重要[1-4]。然而,由于结构中传感器安装数量与位置受限、传感器类型缺乏或数据采集成本较高等原因,往往难以直接测得所需信息[5-6]。因此,研究基于有限测量响应识别结构载荷并重构其余位置响应的技术具有十分重要的意义。
目前,结构响应重构方法主要有三种:第一种基于卡尔曼滤波类[7-8];第二种基于经验模态分解[9-10];第三种基于结构传递矩阵。王娟等[11]在未知激励的条件下,利用部分测点的动态响应结合传递矩阵重构其他未测量位置处的响应,并采用正则化方法改善重构方程的病态性。Zhang等[12]基于状态空间模型推导应变重构方程,通过已知应变响应结合传递矩阵重构结构未知应变响应,并利用应变标准差曲线定位结构损伤。
上述方法都在不计算载荷的情况下,直接由结构已知响应重构出未知响应。然而,Liu等[13]指出基于传递矩阵的响应重构过程中实际包含载荷的识别,二者应综合考虑。同时他还用实测加速度响应结合传递矩阵计算结构载荷、重构未知加速度响应,并通过快速收缩阈值算法改善传递矩阵的病态性和缓解冲击力稀疏性的影响。Li等[14]在考虑结构载荷和响应测量不确定性的情况下,提出一种基于稀疏贝叶斯框架的算法来同时识别载荷的位置和时间历程,并重构结构响应。而结构载荷识别的实质就是根据已知系统的动态特性和实测响应来计算动态载荷,是一个典型的不适定逆问题[15],传递矩阵的病态性,易放大噪声对测量响应的影响,从而降低结构载荷识别与响应重构的精度。
为了解决载荷识别过程的不适定问题,通常采用正则化技术。常见的正则化方法有:奇异值分解(singular value decomposition, SVD)[16-17]、Tikhonov正则化[18-19]和迭代正则化[20-21]等。因迭代正则化算法的迭代过程就是正则化过程,不需要显式的正则化参数等优点,被广泛应用于求解不适定问题中。然而,Fong等[22]指出最小二乘QR分解(least square QR, LSQR)与最小平方残差(least square minimal residual, LSMR)算法在解决不适定问题时存在半收敛行为,若对迭代终止次数的估计不精确易导致结果出现较大的误差。因此,Li等[23]在振动信号滤波降噪的基础上,采用Tikhonov正则化方法对LSQR迭代算法进行了预优化,解决当噪声较大时LSQR的不收敛现象,并用于识别洪流结构振动的载荷。Rezaiee-Pajand等[24-25]指出LSMR具有比LSQR更早终止迭代的优势,并结合Lanczos双对角化算法和Tikhonov正则化技术改善LSMR的半收敛行为,提出一种基于灵敏度的单元质量矩阵和刚度矩阵同步更新的有限元模型修正方法。然而,LSMR算法及其改进算法多应用于图像去噪领域,Chung等[26]充分讨论了LSMR确定最优正则化参数的各种方法及其停止准则,并用于去除图像噪声。但此问题仍需要进行更深入研究,以期将其应用到结构载荷识别与响应重构领域,提高结构载荷识别精度。
基于以上问题,本文将LSMR算法引入结构载荷识别与响应重构领域,并用Tikhonov正则化方法处理LSMR算法的投影问题,解决半收敛现象,从而得到一种混合正则化方法,将其用于解决载荷识别问题的不适定性,提高载荷及响应的重构精度。首先,基于时域状态空间模型构建结构传递矩阵,并建立载荷识别与响应重构方程;然后,采用混合正则化方法改善载荷识别方程的不适定性,得到载荷的正则化解,再结合响应重构方程的传递矩阵对结构的位移、速度和加速度响应进行重构;最后,分别对简支梁模型进行数值仿真和试验分析,验证所提方法的可行性。
1 理论背景
1.1 状态空间模型
对于线性系统,其动力学方程可表示为
(1)
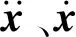
通过x(t)=Φq(t)模态坐标变换,动力学方程转化为模态坐标形式
(2)
式中:q为模态坐标;ε为模态阻尼比矩阵;ω为特征频率矩阵;Φ为结构模态振型矩阵。
(3)
式中:j=1,2,…,Nt,Nt为采样点数;y(j)为结构载荷向量;A、B、G和D分别为离散方程的状态矩阵、输入矩阵、输出矩阵和直接传输矩阵,其表达式为
(4)
(5)
(6)
(7)
经过迭代运算,式(3)可表示为
(8)
假设零初始条件z(0)=0;f(0)=0;式(8)可表示为
(9)
式(9)为结构响应与载荷之间的关系式,可简化为
Y=HF
(10)
式中:Y为结构全部响应向量组合;F为结构全部载荷向量组合;H为结构传递矩阵。
1.2 载荷识别与响应重构方程
假设系统已知测点响应为Ykn,未知测点响应为Yun,建立载荷与响应的重构方程
Ykn(Nm×Nt)×1=Hkn(Nm×Nt)×(Nf×Nt)F(Nf×Nt)×1
(11)
Yun(Nr×Nt)×1=Hun(Nr×Nt)×(Nf×Nt)F(Nf×Nt)×1
(12)
式中:Nm为结构可安装传感器数量;Nf为结构所施加载荷数量;Nr为结构需重构位置数量。时域分析中,被测响应数量应不小于外部载荷数量(Nm≥Nf)。
由式(11)可知,若已知测量响应Ykn和传递矩阵Hkn,则可识别出未知激励力F
(13)
式中: 上标“+”为矩阵Moore-Penrose广义逆。式(13)代入式(12)可重构出所需重构位置的响应。
因此通过上述过程,也可实现由已知测量响应重构未知响应
(14)
由式(13)、式(14)可知在识别载荷时,传递矩阵Hkn广义逆的求解是载荷识别与响应重构过程中的一个关键步骤。而在实际工程中,传递矩阵的病态性会放大测量噪声的干扰,导致采用传递矩阵广义逆的求解精度较低,影响载荷识别和响应重构结果。因此为了得到式(13)的稳定解,需对其进行正则化处理。
2 求解不适定问题的混合正则化方法
2.1 LSMR
LSMR算法是最小二乘方程的迭代求解器,适用于求解稀疏矩阵线性方程组。其目标函数为
(15)
式中,rk=Ykn-HknFk为残差向量,Fk为第k次迭代载荷值。
LSMR算法采用GK(Golub-Kahan)双对角化过程生成Krylov子空间。双对角化算法是一种正交矩阵分解,通常给定矩阵Hkn和向量Ykn,会产生两个正交矩阵以及一个双对角矩阵。GK过程公式如下
β1u1=Ykn
(16)
(17)
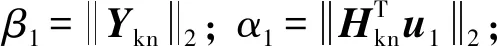
βk+1uk+1=Hknvk-αuk
(18)
(19)
GK过程k次迭代之后,可得正交矩阵Uk=[u1,…,uk]和Vk=[v1,…,vk],双对角矩阵Bk
式(16)~式(19)可以递归为
HknVk=Uk+1Bk
(20)
(21)
式中:Lk+1=[Bkαk+1ek+1],ek+1是维数为(k+1)·(k+1)的单位矩阵的最后一列。
(22)
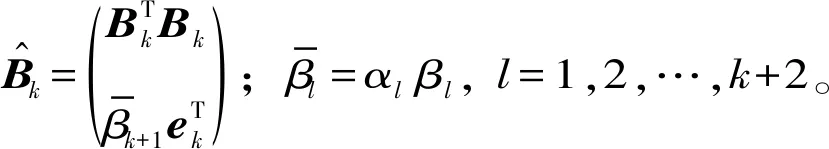
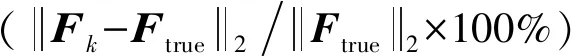
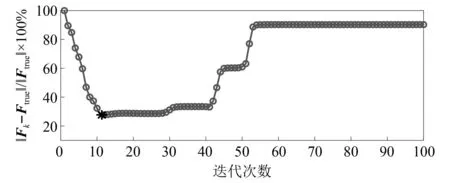
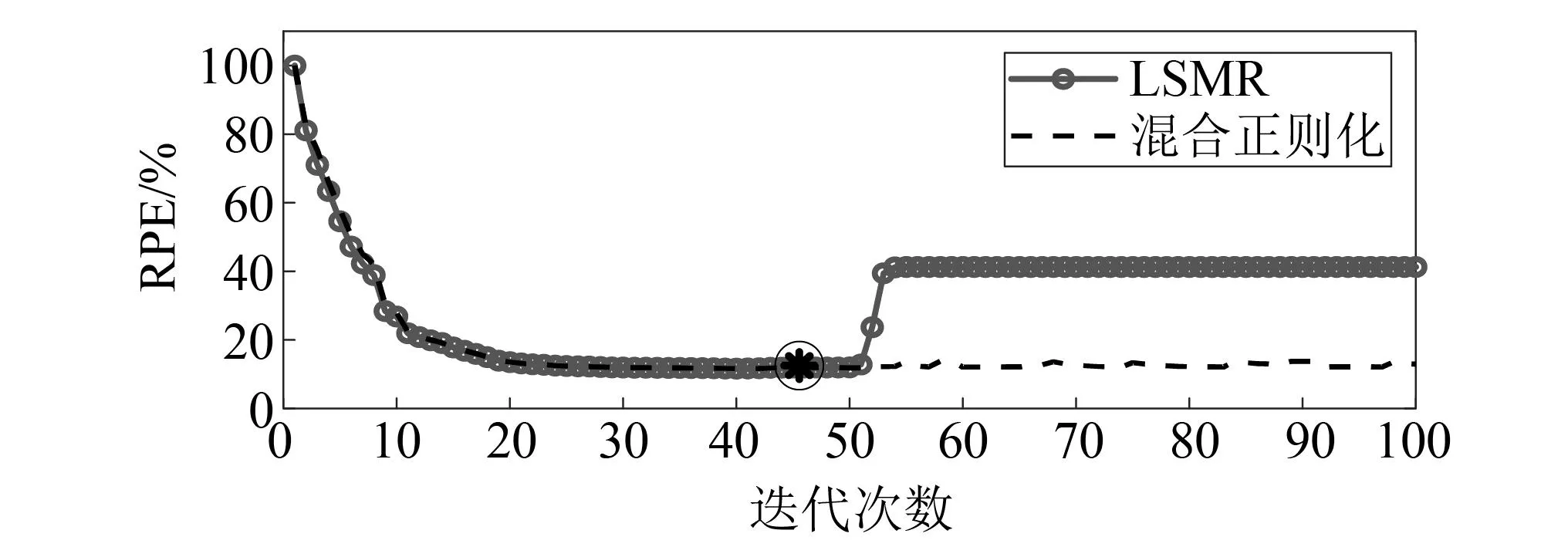
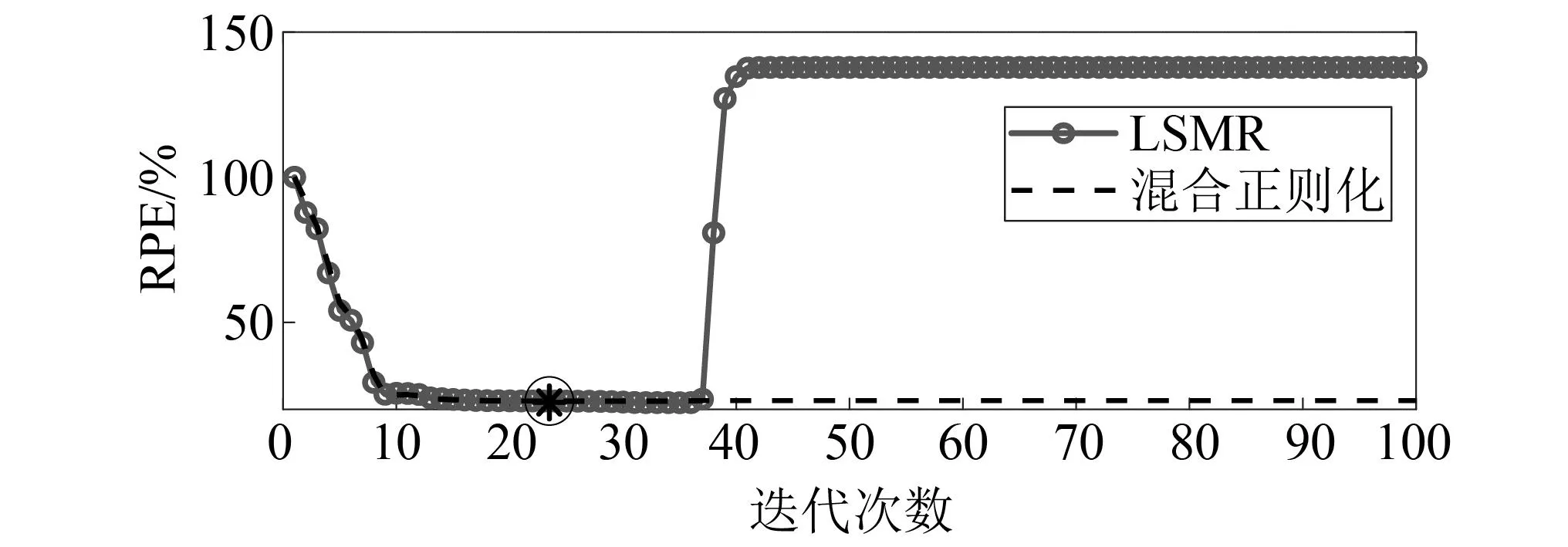
图1 LSMR算法的半收敛现象Fig.1 Semi-convergence of LSMR algorithm
2.2 混合正则化方法
混合正则化方法将LSMR算法与著名的Tikhonov正则化技术相结合,利用LSMR的迭代算法,将原病态逆问题投影到维数小但维数增加的Krylov子空间上。随后在每次迭代中使用Tikhonov正则化技术对投影问题进行处理,并采用GCV(generalized cross-validation)准则自适应选择正则化参数。因此混合正则化方法具有两个主要优点:①克服LSMR算法在噪声条件下的半收敛行为;②在每次迭代中自适应选择正则化参数。
混合正则化方法求解式(22)的表达式如下
(23)
则式(23)的解为
(24)
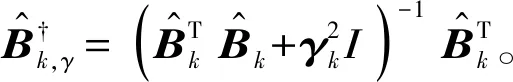
最后用所提方法求解不适定问题HknF=Ykn可得载荷值
(25)
2.2.1 选择正则化参数
混合正则化方法通过最小化GCV函数,在第k次迭代时得到最优正则化参数γk,且在每次迭代时都能自动选择一个正则化参数,不需要先验估计。GCV函数表达式为
(26)
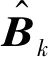
GΙ(γk)=
(27)
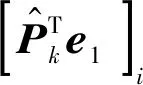
2.2.2 迭代停止准则
确定迭代的停止准则也是混合正则化方法的关键,该准则确定最终迭代停止的次数k。因此本文引入一个新的GCV函数考虑该问题,表达式为
(28)
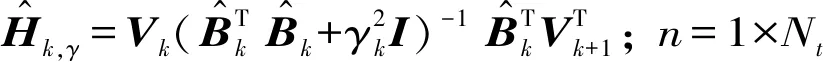
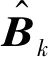
GⅡ(k)=
(29)
混合正则化方法满足下列条件之一便停止迭代,输出迭代次数k: ①达到指定最大迭代次数(根据多次数值仿真及试验分析结果,本文指定最大迭代次数Kmax=100); ②函数GⅡ(1)~GⅡ(Kmax)中的最小值; ③满足式(30),其中本文公差δ=1×10-10。
(30)
2.2.3 算法步骤
由2.2.1节和2.2.2节分析可知,正则化参数γk最初是通过在第k次迭代时最小化GⅠ(γk)得到,然后将该值代入GⅡ(k)中选择终止次数,一旦确定迭代终止次数k,便可输出最优正则化参数γk。因此,确定正则化参数和迭代次数的过程是同时实现的。
混合正则化方法求解载荷的具体步骤如下:
步骤1输入Hkn、Ykn、δ和Kmax。
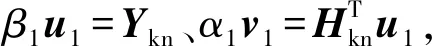

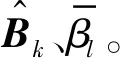
步骤5通过最小化GⅠ(γk)确定正则化参数γk,k=2,3,…,Kmax。
步骤6将所得正则化参数代入式(29)计算GⅡ(k),k=2,3,…,Kmax。
步骤7若满足迭代停止条件则输出最终迭代次数及最优正则化参数,若不满足迭代停止条件,则返回步骤5。
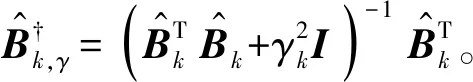
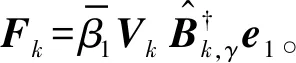
3 载荷识别与响应重构流程
基于混合正则化方法的结构载荷识别与响应重构流程图,如图2所示。
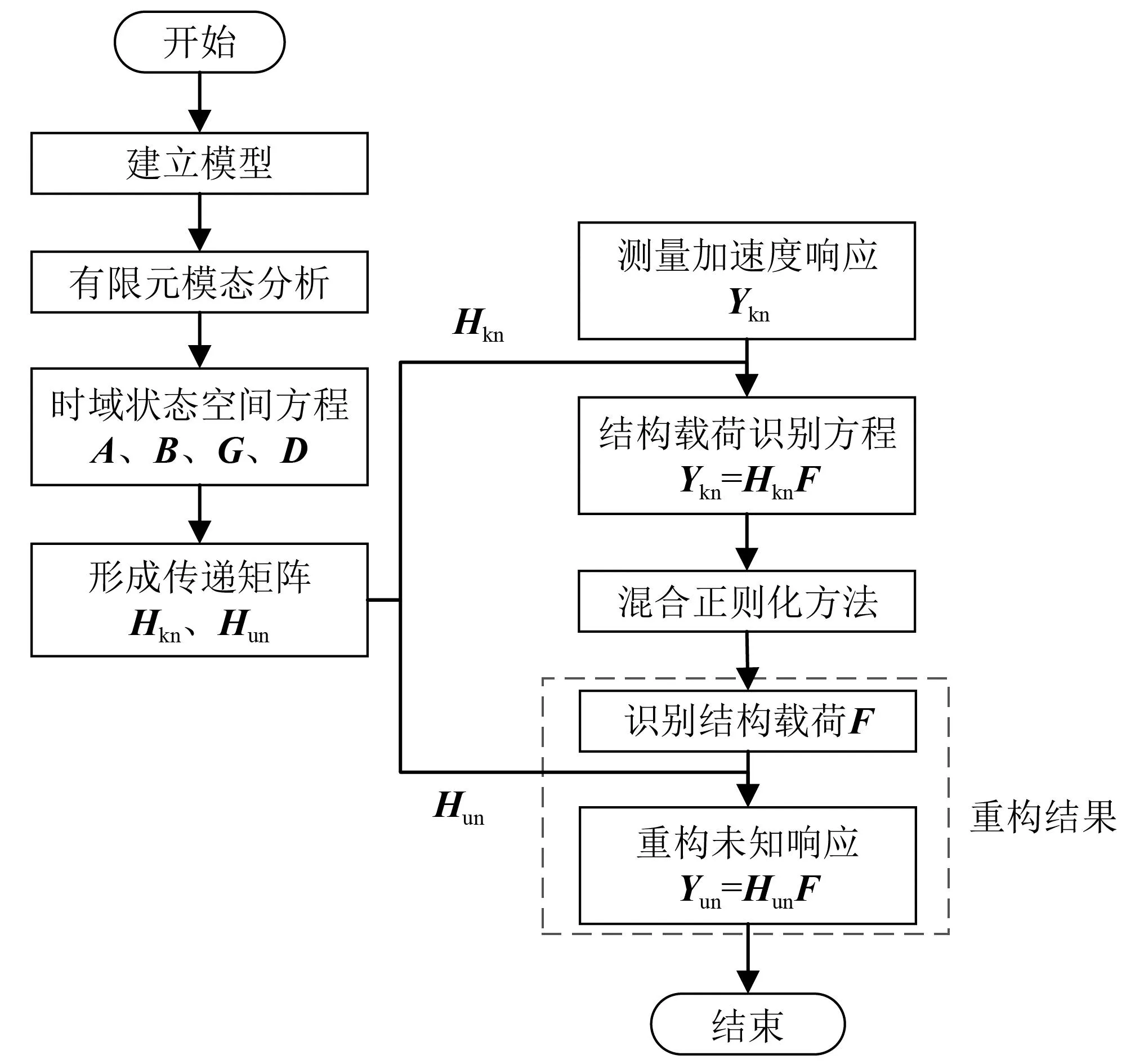
图2 载荷识别与响应重构流程图Fig.2 Flowchart of load identification and response reconstruction
4 数值算例
在ANSYS软件中建立矩形截面简支梁模型进行数值仿真研究,梁单元类型为Beam3,如图3所示。该矩形截面简支梁模型长、宽和高分别为2 000 mm、100 mm和10 mm,并将其划分为20个单元,21个节点。弹性模量、材料密度和泊松比分别为210 GPa、7 800 kg/m3和0.3,阻尼比ε=0.01。在梁两端(即1节点和21节点)分别施加固定约束和简支约束,且仅考虑垂直方向的振动。由于高阶模态对整体结构振动响应影响较小,故计算过程中常选用对振动响应影响较大的低阶模态,本文选取前5阶模态为目标模态进行结构载荷识别与响应重构,前5阶固有频率为5.86 Hz、23.46 Hz、52.83 Hz、94.20 Hz、148.10 Hz。
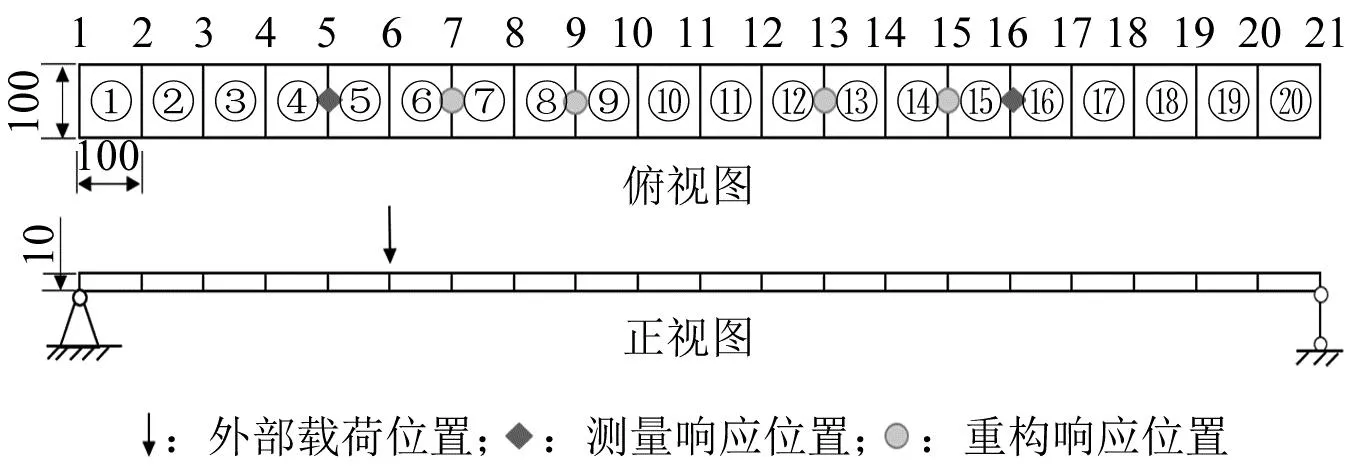
图3 简支梁模型(mm)Fig.3 Simply supported beam model (mm)
在数值仿真中,考虑实际工程中的噪声干扰,在计算响应中加入服从正态分布的随机噪声
Ykn=Ytrue+Lnoise×std(Ytrue)×randn
(31)
式中:Ykn为加噪声后的测量加速度响应;Ytrue为有限元计算的真实加速度响应;Lnoise为噪声水平; std(·)为标准差; randn为均值为0,标准差为1的正态分布随机数。
为了探究载荷识别和响应重构的精度,定义如下相对百分比误差(relative percentage error, RPE)
(32)
(33)
式中:ef和ey分别为载荷和响应的相对百分比误差;Fid和Yid分别为重构的载荷和响应;Ftrue和Ytrue分别为实际计算的载荷和响应。
4.1 所提方法对载荷识别与响应重构的效果
考虑5%(Lnoise=5%)测量噪声干扰,在第6节点垂直方向施加锤击激励,采样频率为1 000 Hz,并提取第5和第16节点加速度响应作为测量响应,去重构结构载荷、第7节点的位移响应、第9节点的速度响应以及第13和第15节点的加速度响应。
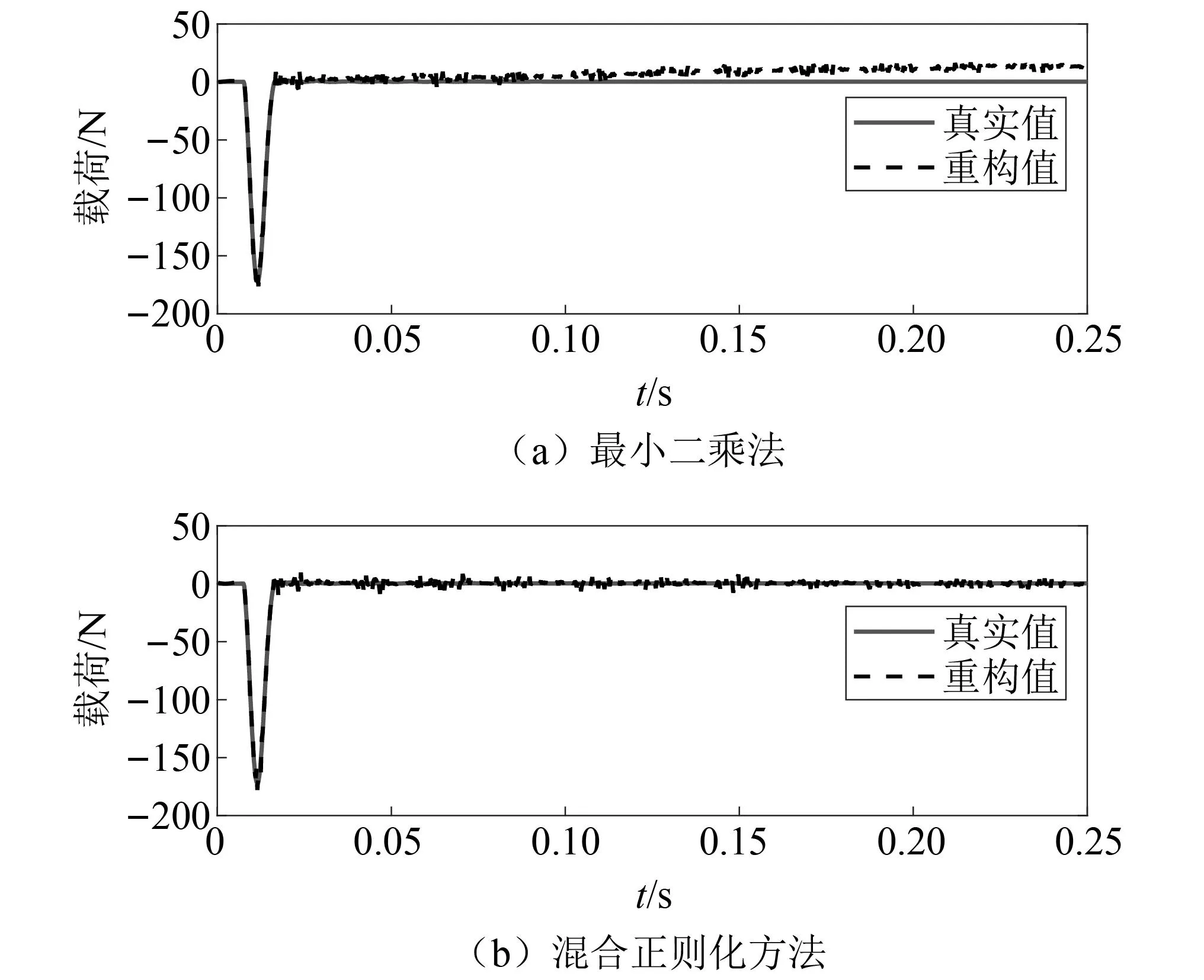
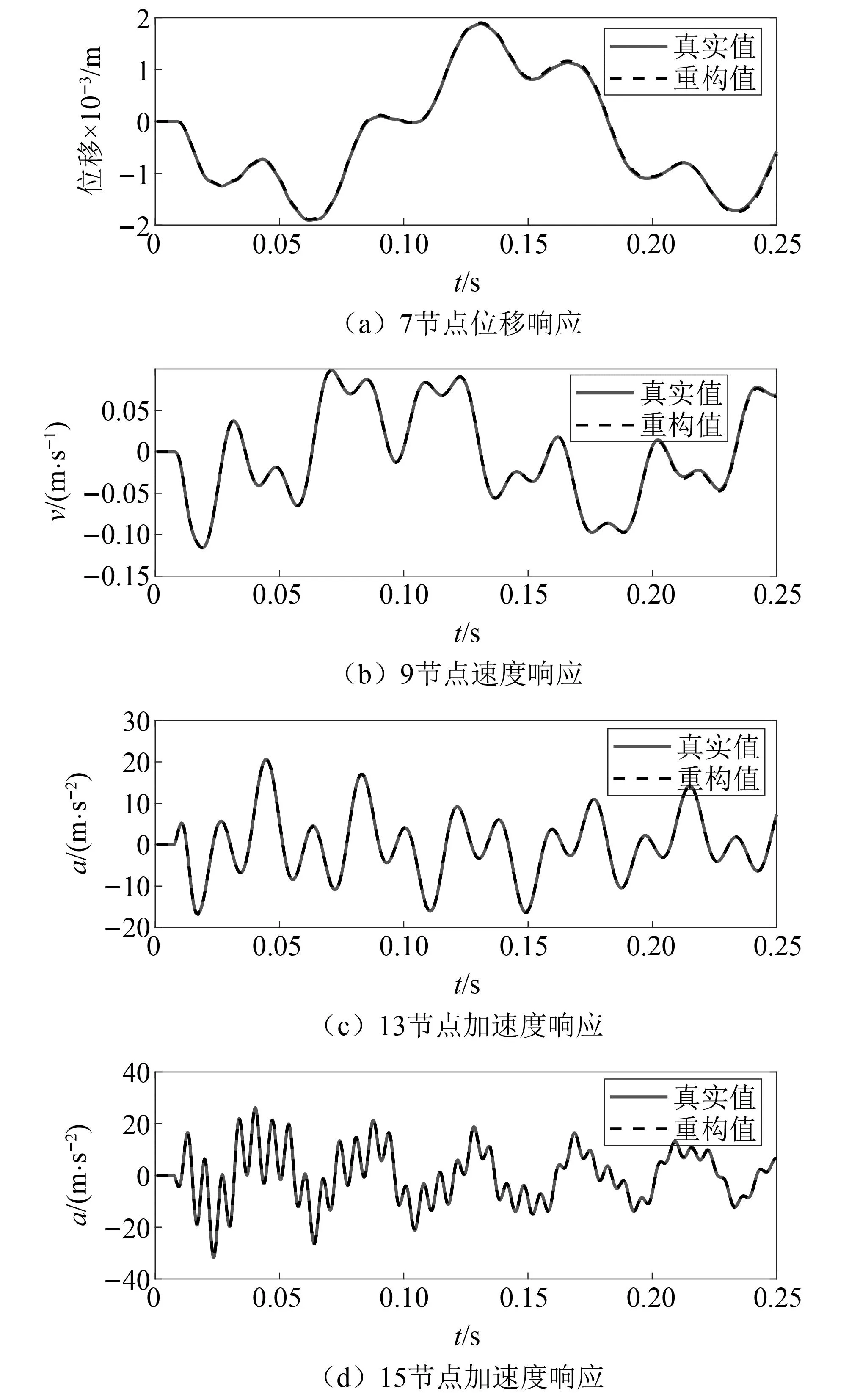
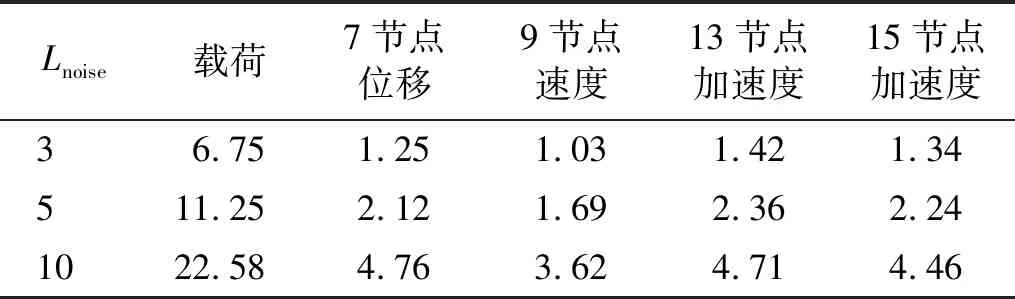
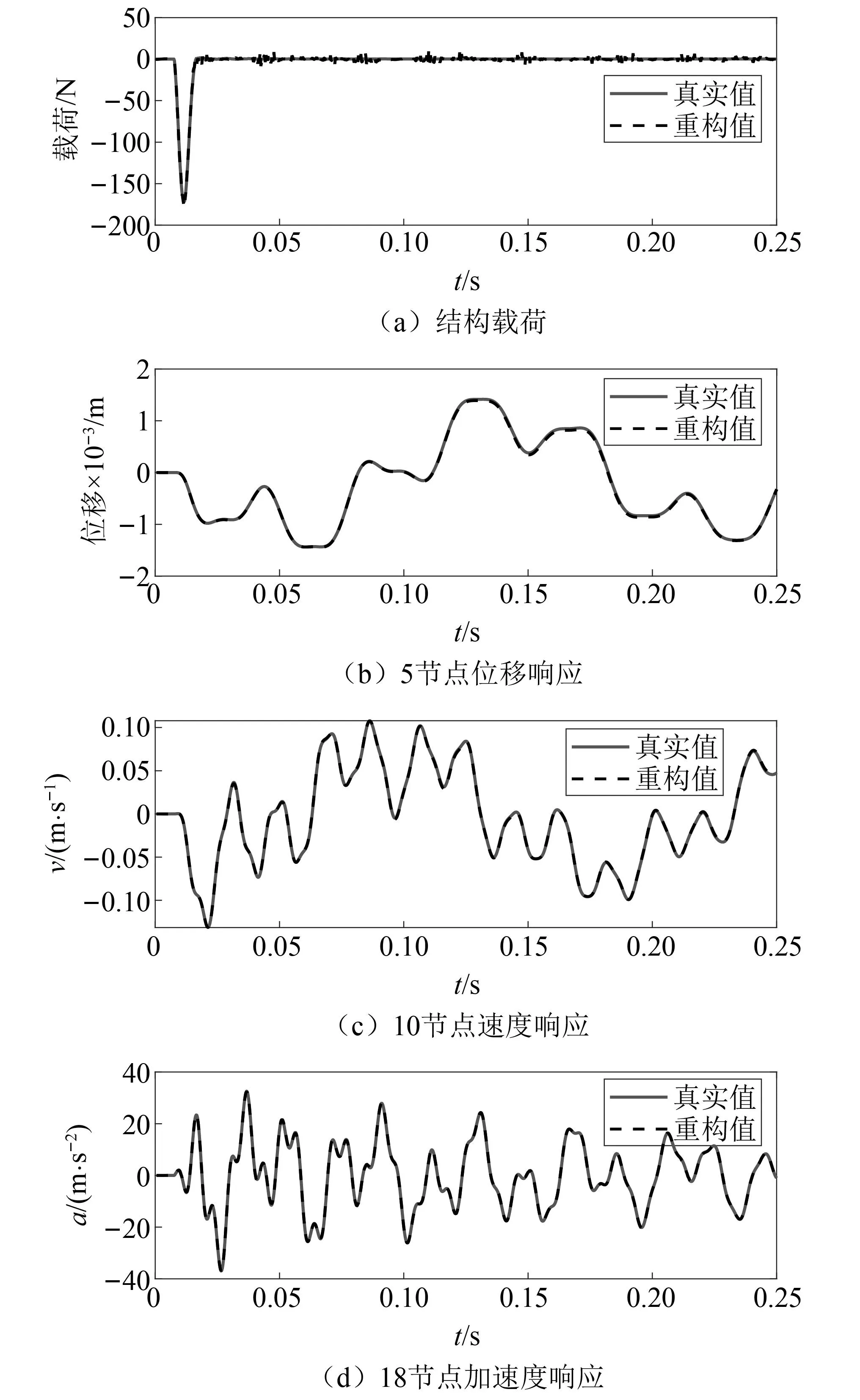
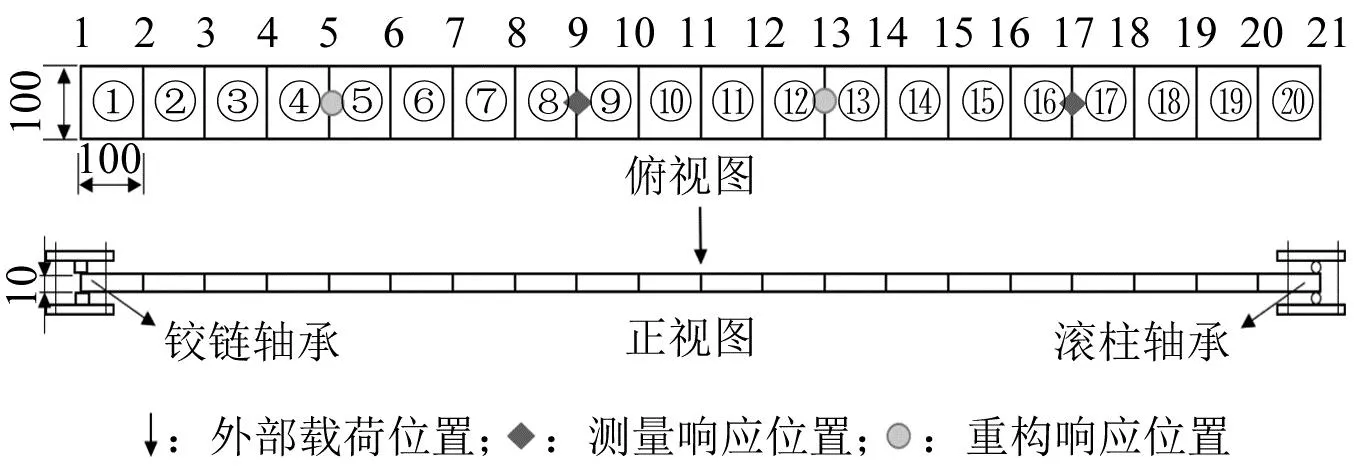
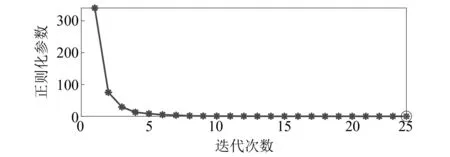
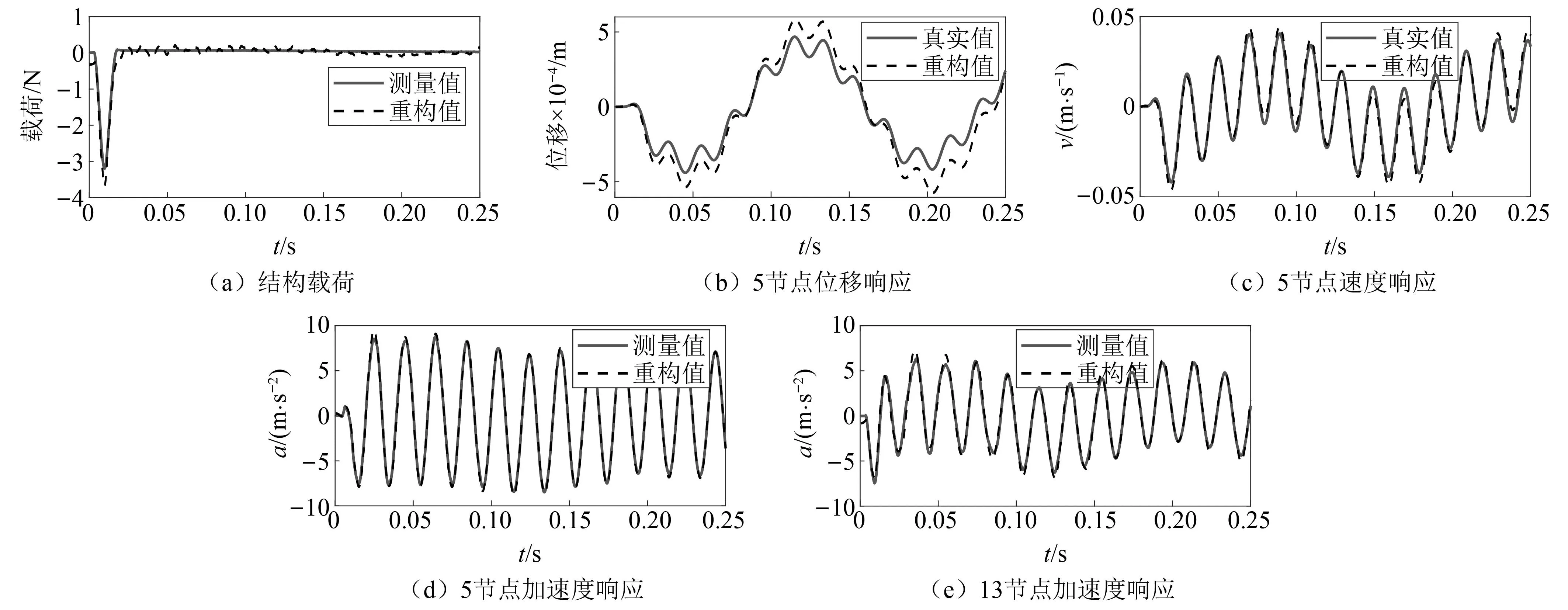
每次迭代时计算GⅠ(γk)所得的正则化参数,如图4所示。并计算GⅡ(k)确定停止次数k=45,最优正则化参数γk=4.70×10-5用圆圈标出。LSMR算法和混合正则化方法在每次迭代时所识别载荷的RPE图,如图5所示。由图5可知,迭代后期LSMR算法所得载荷的RPE值有所增大,第Kmax=100次迭代所得载荷已不是该算法识别的最优载荷值。而混合正则化方法在k=45 图4 迭代次数与正则化参数Fig.4 Iterations and regularization parameters 图5 相对百分比误差Fig.5 Relative percentage error 在5%噪声水平的干扰下,最小二乘方法和本文所提方法的载荷识别结果如图6所示。由图6可知,当载荷识别方程不适定时,LS方法识别的载荷偏离真实值,而本文所提方法的载荷识别值与真实值吻合较好,其中两种方法识别出载荷的RPE值分别为41.26%和11.25%。说明当载荷识别问题不适定时,所提正则化方法可提高载荷识别精度,求解出较为准确的载荷值。 图6 载荷真实值与重构值对比Fig.6 The true value versus the reconstructed value of the load 本文所提方法下各类型响应的重构结果,如图7所示。由图7可知,各类型响应的重构值与真实值也能较好吻合。说明所提方法有效改善了载荷识别问题的不适定性,从而可以利用有限测点加速度响应识别结构外部载荷并重构结构各类型响应。 图7 响应真实值与重构值对比Fig.7 The true value versus the reconstructed value of the response 为了探究在不同噪声水平下,所提方法对结构载荷与各类型响应的重构情况,作如下研究:在保持载荷作用位置及响应测量位置不变的情况下,分别在测量加速度响应中加入3%、5%和10%三种等级的测量噪声。 结构载荷和各类型响应的重构RPE值,如表1所示。由表1可知,随着噪声水平的提升,结构载荷与各类型响应的RPE值逐渐增大,但在10%的噪声水平下,结构载荷与各类型响应的重构RPE值仍控制在22%和5%左右,在工程可接受的范围内。外部载荷的RPE值要远大于结构位移、速度和加速度响应,因为在进行响应重构时,传递矩阵Hun可以减小载荷的重构误差,使各类型响应的重构值与真实值更接近。综上可知,噪声水平对载荷及各类型响应的重构精度有一定影响,但仍能对其进行有效重构。 表1 不同噪声水平下的相对百分比误差Tab.1 RPE at different noise levels 单位:% 为了进一步探究传感器位置发生变化时,所提方法对结构载荷与各类型响应的重构情况,在5%的噪声水平下,随机选取两组方案下的不同测点及重构点进行对比研究。第一组,选取第8和第12节点为测量位置,重构结构载荷、第11节点的位移响应、第4节点的速度响应以及第16节点的加速度响应;第二组,选取第6和第14节点为测量位置,重构结构载荷、第5节点的位移响应、第10节点的速度响应以及第18节点的加速度响应。 两组方案下传感器测量位置和重构位置发生变化时,所提方法确定的迭代停止次数和最优正则化参数,以及载荷和各类型响应的重构RPE值,如表2、表3所示。由表2、表3可知,当测点发生变化时,载荷的RPE值并未发生较大变化,且重构出的不同位置的各类型响应RPE值均控制在5%以下。说明所提方法受测点变化的影响不大,对测点变化具有一定的鲁棒性。 表2 迭代次数及最优正则化参数Tab.2 Iterations and optimal regularization parameter 表3 不同测点下的相对百分比误差 为了更加直观地表示其他位置的重构情况,以第二个方案的测点和重构点为例,将其载荷和响应的重构值与真实值进行对比,如图8所示。由图8可知,当测点位置发生变化时,所提方法仍能较好地识别结构载荷并重构其他位置的各类型响应。 图8 真实值与重构值对比Fig.8 The real value versus the reconstructed value 为了进一步验证所提方法的有效性,仍以简支梁为试验对象,如图9所示。简支梁的几何尺寸、单元划分与数值仿真中相同。依旧仅考虑垂直方向的振动响应,选取前5阶模态振型为目标模态进行结构载荷识别与响应重构,结构前5阶固有频率和阻尼比如表4所示。试验过程所采用的加速度传感器型号为ICP型的INV9821;网络分布式采集仪为北京东方振动和噪声技术研究所的INV3062-C2;模态试验选用5 000 kg大力锤,响应试验选用500 kg小力锤。 表4 模型固有频率和阻尼比 图9 简支梁试验模型Fig.9 Simply supported beam test model 如图10所示,在第11节点垂直方向施加锤击激励,采样时间取0.25 s,采样频率为1 000 Hz;在第5、第9、第13和第17节点布置4个加速度传感器。第9和第17节点为测量位置,由于试验过程无法获得不含噪声的真实响应,故用传感器采集的加速度测量响应代替真实响应用于识别结构载荷并重构未知的各类型响应;第5和第13节点为重构位置,传感器测得的加速度响应用于重构效果对比。同时重构第5节点的位移和速度响应,但由于无法获得第5节点位移和速度响应的测量值,故与状态空间方程计算出的真实值做重构效果对比。 图10 传感器布置(mm)Fig.10 Sensor arrangement (mm) 如图11所示,为所提方法计算的迭代停止次数k=24,以及最优正则化参数γk=2.54×10-2,并用圆圈标出。两种方法在每次迭代时所识别载荷的相对百分比误差,如图12所示。由图12可知,混合正则化方法能有效改善LSMR算法的半收敛行为,提高载荷识别精度。 图11 迭代次数与正则化参数Fig.11 Iterations and regularization parameters 图12 相对百分比误差Fig.12 Relative percentage error 结构载荷与各类型响应的重构效果如图13所示。由图13可知,结构载荷、速度响应及加速度响应的重构值与测量值(或真实值)曲线吻合较好,位移响应的重构值与真实值曲线吻合略差。 图13 载荷与响应的重构对比Fig.13 Reconstruction comparison of load and responses 载荷、第5节点位移、速度、加速度和第13节点加速度响应的重构的RPE值如表5所示。由表5可知,重构出的位移和速度响应的RPE值较加速度响应的大。可能存在原因分析:①位移和速度响应为状态空间方程计算值,但用于重构的加速度响应为传感器的实测值,所以重构时曲线略有偏差;②所提方法下载荷识别的RPE值较大,而位移对载荷信息较敏感。因此后续研究中还应增加对位移响应的测量。 表5 载荷与各类型响应的RPE 本文提出一种可以有效改善载荷识别与响应重构问题不适定性的混合正则化方法,得到如下结论: (1) 所提方法能有效改善重构方程的不适定问题,仅利用有限测量加速度响应实现对结构载荷及位移、速度和加速度响应的有效重构。 (2) 在噪声水平及测点变化的情况下,所提方法仍能对结构载荷及多类型响应进行有效重构,说明此方法具有一定的鲁棒性。 (3) 对简支梁的数值仿真和试验分析均验证了所提方法的可行性与有效性,为结构载荷识别与响应重构提供了一种新方法。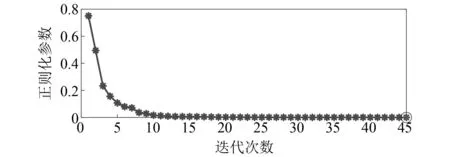
4.2 测量噪声水平对所提方法重构效果的影响
4.3 测点布置对所提方法重构效果的影响


5 试验验证



6 结 论

