预应力混凝土梁-型钢混凝土柱新型框架节点受剪承载力计算方法

潘钻峰，葛 雄，曾 滨，许 庆

(1.同济大学土木工程防灾国家重点实验室，上海 200092；2.云南省设计院集团有限公司，昆明 530100；3.中冶建筑研究总院有限公司，北京 100088)

梁柱节点是框架结构中重要的结构部位，它是梁柱构件的传力枢纽，受力较为复杂；尤其是在抗震设计环节，节点的抗震性能直接影响结构安全性[1]。国内外多次地震的经验教训表明：框架节点的受剪承载力是影响框架结构整体抗震能力的关键因素之一[2-3]。对钢筋混凝土框架节点受力机理及其承载力计算方法的研究一直受到国内外研究学者和工程界的广泛重视[4-5]，但由于节点应力状态的复杂性及影响因素的多样性，目前各国学者对节点受剪分析模型尚未形成统一的看法，导致各国规范在节点受剪承载力的计算方面大多是基于试验结果的半经验半理论公式。

设计预应力混凝土框架时，如裂缝控制要求较为严格，容易出现预应力混凝土梁承载力较高，加上楼板对梁承载力的提高作用，往往难以实现“强柱弱梁”的耗能机制，难以满足抗震设计要求。针对该现象，本文提出使用型钢混凝土柱，提升框架柱的承载能力与延性，从而实现预应力框架结构的混合耗能机制。研究对象为预应力混凝土梁-型钢混凝土柱新型框架节点，与普通钢筋混凝土框架节点相比，预应力混凝土梁-型钢混凝土柱框架节点区梁柱钢筋交汇，需要进行大量的钢材焊接、开孔穿筋工作，节点受力更加复杂。对于预应力对节点的作用，《预应力混凝土结构抗震设计规程》(JGJ 140-2019)[6]中认为，预应力对混凝土节点的侧向约束作用，使得节点处于双向受压状态，提高了节点的开裂荷载和受剪承载力。赵鸿铁[7]对型钢混凝土节点开展研究，认为节点中型钢的抗剪可视为由柱型钢翼缘与加劲肋构成的封闭钢“框架”和它们包围的型钢腹板“剪力墙”形成的“框架-剪力墙”体系。PARRAMONTESINOS 和WIGHT[8]认为节点承载力应由型钢腹板、混凝土内斜压杆和混凝土外斜压杆组成。傅剑平等[9-10]对钢筋混凝土节点试验发现，节点剪力传递除了斜压杆机构，还应该考虑桁架机构。李振宝等[11]基于拉压杆模型建立了双向受力下框架节点的抗剪承载力计算方法，熊学玉等[12]采用修正软化拉压杆模型分析了钢筋混凝土框架中节点受剪性能。目前还未有文献对预应力混凝土梁-型钢混凝土柱新型框架节点受剪承载力开展研究。

本文在桁架模型与斜压杆模型的基础上，对预应力混凝土梁-型钢混凝土柱框架节点受力机理和节点受剪承载力计算方法开展研究，通过对节点受力模型的理论分析，提出计算节点受剪承载能力的计算方法，并采用已有试验结果对建议方法进行验证。

1 节点受剪机理研究

1.1 框架节点混凝土、箍筋及型钢腹板受剪计算

唐九如等[13]的研究表明：型钢翼缘在节点受剪的各阶段中应变一直很小，直到试件达到极限荷载后，翼缘才会屈服，它的作用主要是对型钢腹板以及混凝土提供约束，翼缘本身并不参与节点抗剪。框架节点受剪主要由箍筋、型钢和混凝土三部分组成，各部分承担的剪力可按如下方法进行计算：

1) 节点核心区总水平剪力的计算

节点核心区受到上下柱端传来的轴力、剪力和弯矩以及左右梁端传来的弯矩、剪力和轴力，如图1(a)、图1(b)所示；梁端、柱端在节点核心区产生的弯矩可等效为力偶，如图1(c)所示；取节点上半部分进行受力分析，如图1(d)所示。

图1 节点受力示意图Fig.1 Schematic diagram for joint force

在水平方向上，由力的平衡可以得到节点核心区的总水平剪力为：

式中：Vc为柱端的水平剪力，其大小为柱端施加的水平荷载；Tb、Cb分别为梁端弯矩等效力偶形成的拉力、压力，其值分别为Mb1/d、Mb2/d，Mb1和Mb2为节点左侧、右侧梁端弯矩；d为梁端截面拉力和压力合力点之间的距离。由节点处弯矩平衡可得：

2) 节点核心区型钢腹板的受剪承载力

型钢腹板处于弹性状态时受剪可按式(4)计算：

式中：型钢腹板中点处剪应力τw=Gsγw；Iw为型钢的截面惯性矩；tw为型钢腹板厚度；Sw为型钢腹板中点处对应的面积矩；Gw为型钢的剪切模量；γw为型钢腹板中点处的应变。文献研究表明[8,14]：当节点接近极限状态时，腹板截面上达到剪切屈服应力状态的面积超过80%，可认为此时应力呈梯形分布，所以此时型钢腹板承担的剪力为：

3) 节点核心区箍筋的受剪承载力

节点核心区箍筋承担的剪力可按式(6)计算：

式中：Vsv为箍筋拉力；Esv为箍筋弹性模量；Asv1为与核心区临界裂缝相交的单肢箍筋截面积；为箍筋的实测平均应变；n′为有效的核心区箍筋总肢数。对于n′的取值，文献研究表明[15-16]：不同位置的箍筋得抗剪效率不一致，靠近节点中部的箍筋抗剪效率更高，所以可将节点中部50%高度范围内的箍筋取实际箍肢数量，外部50%的高度范围内的箍肢数量取一半，即将实际箍肢数量乘上0.75 倍得到有效箍肢数量，n′=0.75n，n为核心区实际箍筋总肢数。

4) 节点核心区混凝土受剪承载力

混凝土的受力状态相对复杂，应变在各阶段受力过程中难以准确获得，采用节点总水平剪力减去箍筋和型钢腹板的贡献而获得，如式(7)所示：

1.2 新型框架节点受剪模型

预应力混凝土梁-型钢混凝土柱框架节点还需考虑预应力对节点的增强作用，本文将同时考虑斜压杆机构和桁架机构对节点受剪承载力的贡献。箍肢的约束作用提高了斜压杆混凝土的承载力，可以通过Mander 模型[17]进行计算，得到约束混凝土的应力-应变关系。由于不考虑混凝土的抗拉强度，所以实际模型中只考虑斜压杆的作用，不考虑斜拉杆的影响，认为框架节点核心区的剪力主要由外部混凝土斜压杆、内部混凝土斜压杆、型钢腹板以及节点区箍筋来承担。各抗剪部分受力简图如图2所示。混凝土斜压杆依据受约束的强弱分为内外斜压杆：内斜压杆对应强约束区，受箍筋、型钢共同约束；外斜压杆对应弱约束区，仅受箍筋约束。

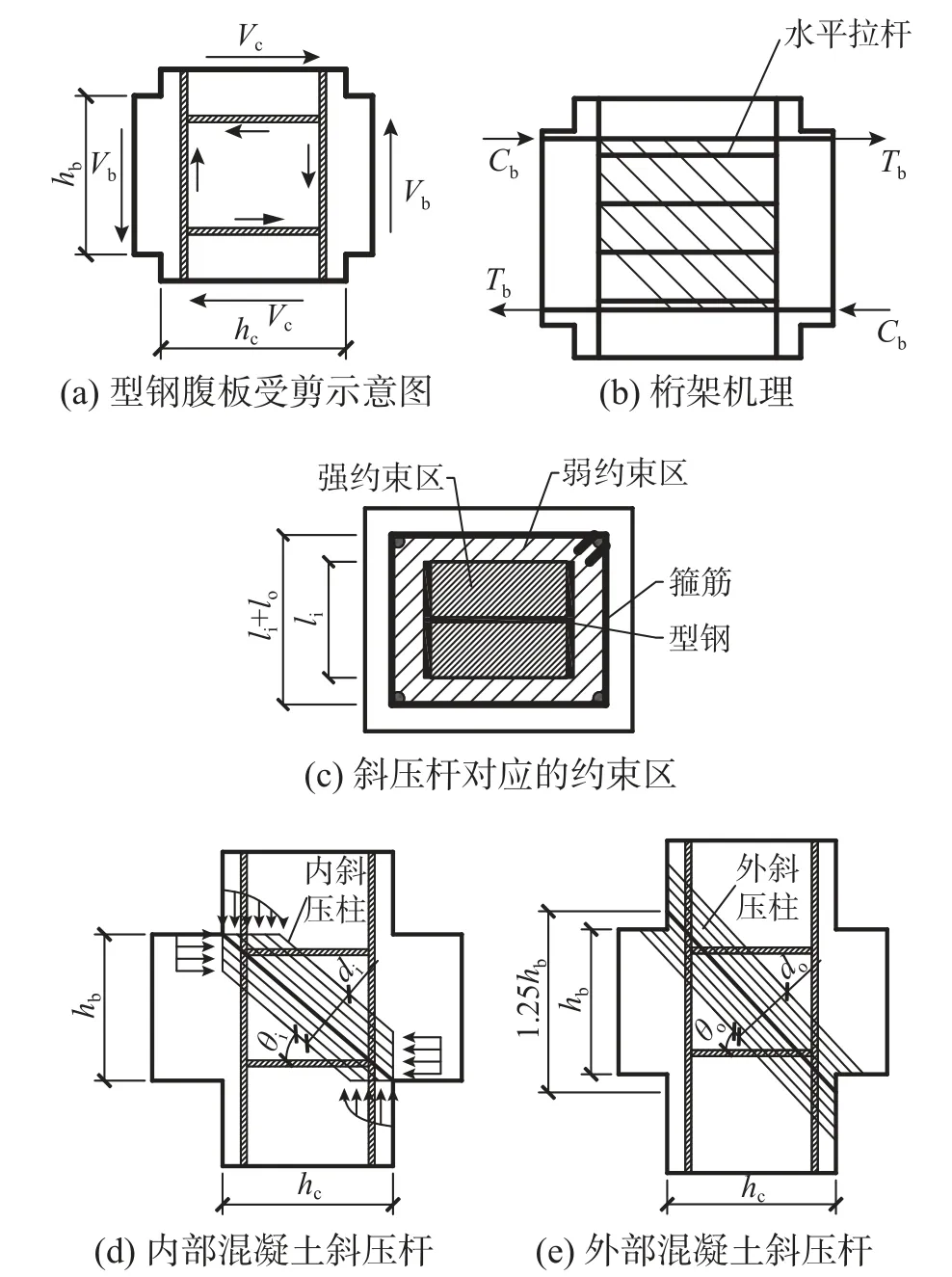
图2 新型框架节点受剪示意图Fig.2 Schematic diagram for shear analysis of a new type of frame joint

值得注意的是，当节点均发生梁端弯剪破坏时，节点区域虽然出现了裂缝，腹板也有部分区域发生了屈服，但箍筋尚未达到屈服应变，节点核心区混凝土也并未发生压碎和剥落，由试验得到的承载力峰值并不代表节点核心区真正的受剪承载力。所以在节点受剪承载力计算时，不能直接代入材性试验得到的屈服强度。本文通过理论计算的方法将承载力计算与节点变形分析结合起来，从而获得节点承载力和节点变形的关系曲线，曲线的峰值就是节点的核心区的极限受剪承载力。

2 新型节点受剪承载力计算方法

预应力混凝土梁-型钢混凝土柱新型框架节点处于压、弯、剪等复合受力状态之下，节点受剪承载力分析不仅要考虑型钢腹板的抗剪贡献，还要考虑预压应力对节点抗剪的约束作用。按照1.2 节的计算模型，节点受剪承载力的计算将由型钢腹板、强约束区混凝土斜压杆和弱约束区的混凝土斜压杆三部分抗剪贡献叠加组成。

2.1 计算假定

依据节点抗剪机理，在充分考虑影响节点受剪承载力的主要因素的情况下，为简化计算，作如下假定：1) 节点核心区受剪承载力的贡献只考虑混凝土、箍筋和型钢腹板三部分的贡献；2) 核心区开裂后，不考虑混凝土抗拉强度；3) 型钢腹板不发生局部屈曲；4) 型钢腹板与混凝土、内部斜压杆混凝土和外部斜压杆混凝土之间粘结性能良好[18]；5) 不考虑加劲板对节点的抗剪贡献。

2.2 型钢腹板

预应力混凝土梁-型钢混凝土柱框架节点中，型钢腹板受到混凝土的约束作用，在达到极限状态前不会发生屈曲破坏。从课题组试验中可知，节点达到承载力极限时，型钢腹板完全屈服，可充分发挥其抗剪作用，在预压应力作用下的型钢腹板处于压剪受力状态，将腹板看作理想弹塑性材料，可得到以下计算公式。

弹性状态时，主拉应力、主压应力分别为：

节点极限状态时，钢腹板适用第四强度理论：

由于钢腹板平面受力，即σ2=0，腹板的剪切屈服应力为：

式中：σc为主轴向压应力；fy为型钢腹板的屈服强度。

故型钢腹板的剪力为：

文献研究表明[8,14]：型钢腹板的剪应变可认为是对称分布的，在距翼缘0.2hf处的应变是腹板中间点最大应变的75%，如图3(a)所示。节点屈服后，腹板截面上达到剪切屈服应力的面积超过80%，可认为此时应力呈梯形分布，如图3(b)所示。

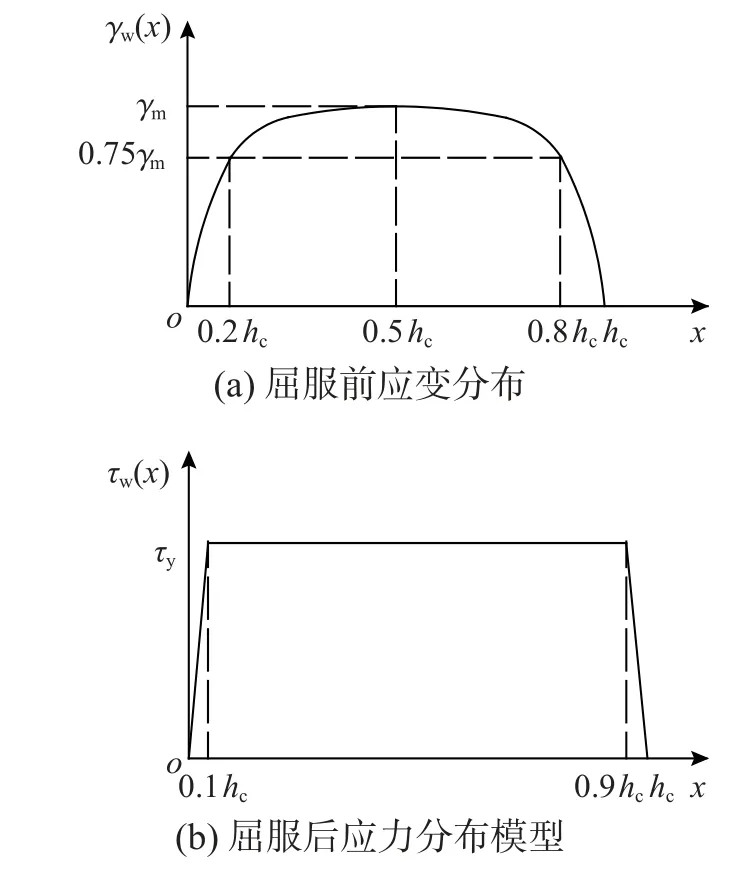
图3 型钢腹板应变分布图Fig.3 Strain distribution of web

腹板剪应变分布按式(12)进行拟合：

故腹板剪应力为：

在计算剪力承载力时，节点腹板若完全屈服或接近于屈服后，可认为腹板剪应力呈梯形分布，则：

2.3 箍筋

箍筋对混凝土提供了约束作用，并且参与构成桁架受力机制，但箍筋提供的受剪承载力仅在节点变形较大时发挥作用。若节点处于弹性状态，或是计算节点核心区的开裂荷载时，可以忽略箍筋的作用；但在计算节点屈服承载力或是极限承载力时，需要考虑箍筋的作用。根据我国现行的《混凝土结构设计规范》(GB 50010-2010)[19]，计算节点承载力时认为所有箍肢均能发生屈服。文献研究表明[15-16]：节点不同位置的箍筋抗剪效率有所差异，箍筋提供的受剪承载力可按式(6)进行计算。

2.4 弱约束区混凝土

研究表明[8,13]：混凝土斜压杆的高度大致为节点对角线长度的1/3，SHEIKH 等[18]认为外侧混凝土斜压柱与水平方向的夹角更大，建议外侧混凝土斜压柱的竖向高度为1.25 倍梁高，如图2(e)所示，所以外侧混凝土斜压柱的高度可按式(15)计算：

外侧混凝土斜压柱与水平向的夹角可按式(16)进行计算：

只需根据斜压杆应变可推知斜压杆的应力，即可计算斜压杆提供的剪力。外部混凝土斜压杆的强度按Mander 模型[17]进行计算，能比较理想地考虑箍筋对混凝土的约束作用。

式中，符号意义见文献[17]。对于一般的截面，MANDER 等[17]给出了双向受力情况下约束混凝土强度确定的方法；DENAVIT 等[20]采用回归的方法得到了不同截面形式下的约束混凝土抗压强度及对应峰值压应变的计算公式。本文为了计算方便，将采用Denavit 公式的约束强度增强系数。计算公式如式(18)～式(19)所示：

式中：εc为无约束混凝土峰值应变；fc为无约束混凝土强度；K值可根据文献[20]计算；无约束混凝土的峰值应变取εc=0.0022。根据节点具体的布置情况，可依据式(18)和式(19)计算得到箍筋约束混凝土的峰值应力和峰值应变。混凝土的弹性模量可按式(20)进行计算[21]：

将混凝土的峰值应力、峰值应变及弹性模量代入式(17)，可以得到约束混凝土的本构模型，如图4 所示。

图4 混凝土约束本构模型Fig.4 Constitutive model of confined concrete

考虑到混凝土的软化效应，本文在承载力计算时将使用Vecchio 和Collins 简化后的混凝土软化模型[22]，用软化系数对混凝土的强度进行折减，但峰值应力对应的峰值应变却不折减。软化系数的计算公式如式(21)所示：

式中：ε1为混凝土的主拉应变；ε2为混凝土的主压应变。最终可得到弱约束区斜压杆水平剪力为：

式中：lo为弱约束区混凝土宽度；do为外侧混凝土斜压杆高度；θo为外侧混凝土斜压杆与水平向的夹角(见图2)；σ 为斜压杆混凝土压应力。

2.5 强约束区混凝土

和弱约束区混凝土斜压杆一致，本文认为强约束区混凝土斜压杆的高度大致为节点对角线长度的1/3，所以如图2(d)所示，内部混凝土斜压杆高度可按式(23)计算：

斜压杆与水平方向的夹角可按式(24)计算：

内部斜压杆的混凝土强度可按Mander 模型[17]进行计算。内部斜压杆除了考虑箍筋的约束作用，还需考虑型钢柱的约束作用，黄维等[23]给出了强约束区型钢对混凝土约束作用的计算方法，型钢对混凝土的附加有效约束力可按式(25)～式(28)计算：

2.6 节点应变方程

各部分剪力计算方法均已确定，只需求解混凝土斜压杆压应变、箍筋拉应变、腹板剪切应变，即可计算节点受剪承载力。节点受力处于平面应变状态，各部分应变关系满足式(30)～式(32)：

式中：εx为水平方向应变；εy为竖直方向应变；γxy为剪切应变；θ 为主压应变方向和水平方向的夹角。上述公式尚不足以求出受剪承载力与剪切应变的关系。通过对唐九如等[13]、刘轩[24]的试验进行研究，可以发现型钢混凝土节点在各受力阶段内，平均主拉应变和平均主压应变的取值可认为呈比例关系，即ktc=ε1/ε2，即可求解出节点承载力和节点剪切应变的关系，在关系曲线上取最值即可得到节点极限承载力。ktc体现了预应力、轴压力等对节点的约束作用，取值越大，约束作用越强，但对各阶段的取值还需进一步探讨。

2.7ktc取值研究

PARRA-MONTESINOS 和WIGHT[14]、贾金青等[15]通过对型钢混凝土框架节点的研究发现，ktc能较好地反映节点的约束水平，ktc取值越大，约束作用越强，并建议在极限承载力计算时，型钢混凝土框架节点取ktc=3.0。由于钢筋混凝土梁承载力较型钢混凝土梁弱，对节点的约束有所减弱；但由于本文研究的是预应力梁，预应力又会增加对节点约束作用。综合考虑，本文在计算极限承载力时偏保守地将ktc取为3.5。为了得到节点受力全过程中的荷载-剪应变关系曲线，对节点屈服前ktc取值进行研究。ktc值在加载过程中是随着裂缝的发展不断变化的，全过程研究比较棘手，因此以初裂状态为切入点进行探讨。众多学者[13,25-26]的研究表明ktc在加载过程中有如下变化规律(如图5 所示)：ktc初始为负值，随着加载变为正值；混凝土开裂后节点的主拉应变总是比主压应变大，因而ktc>1，达到极限状态时取值约为3。节点开裂前处于弹性状态，承载力可近似认为沿直线变化，所以可先确定初裂时ktc的取值，再将初裂与极限状态间的取值线性表示。

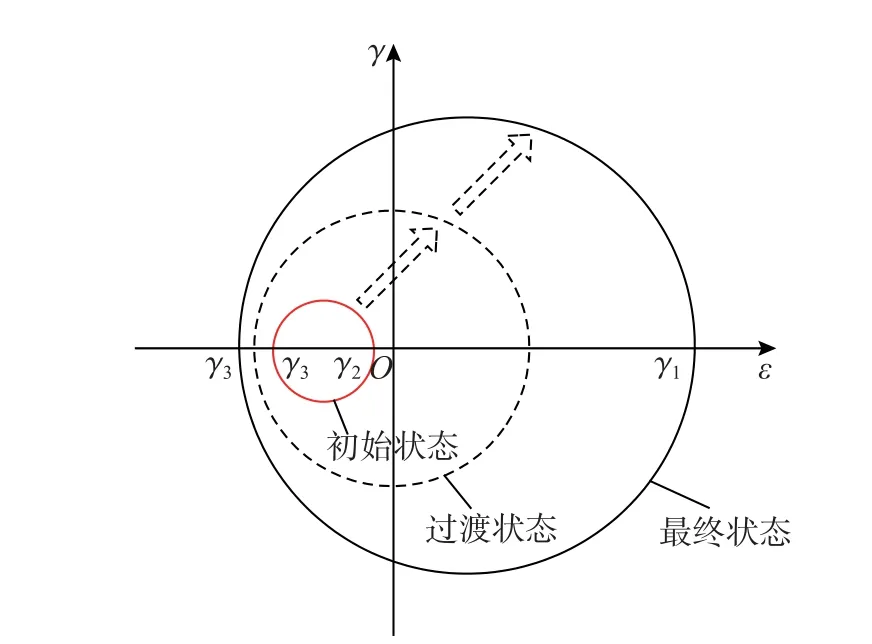
图5 节点应变状态Fig.5 Strain states of joint

对于开裂状态下ktc具体取值，从理论上分析较难获得准确规律，可从试验中进行总结。加载初期，应变片受混凝土的挤压和撕裂影响小，数值上较为准确，这也是可以从试验获取ktc值的基础。唐九如等[13]试验中试件开裂后混凝土和型钢的剪切变形几乎相同，说明二者变形协调，基本无滑移现象；SHEIKH 等[18]的研究表明：随着节点变形的增加，强约束区混凝土与弱约束区混凝土的应变基本相同。所以本文认为型钢腹板、强约束区混凝土、弱约束区混凝土不发生滑移错动，三者节点区的平均主拉、主压应变相同，并用节点区型钢腹板的主拉、主压应变进行表示，开裂阶段数据点整理如图6 所示。

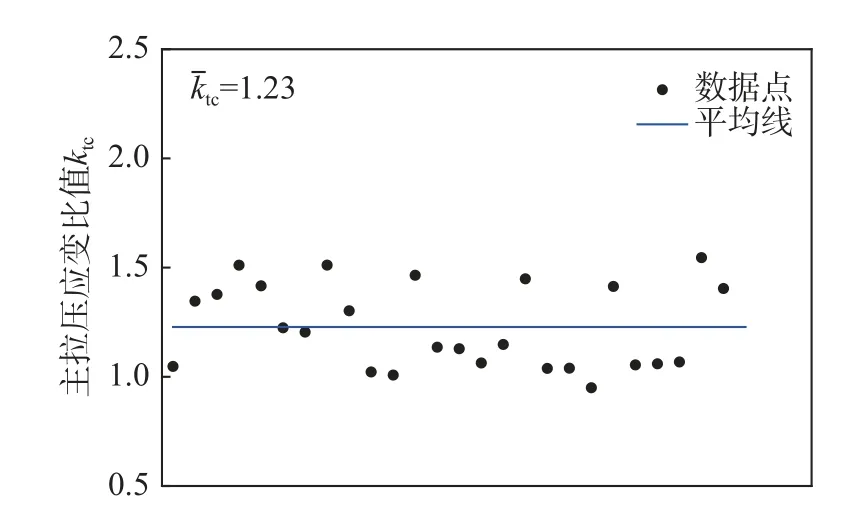
图6 初裂阶段数据ktc汇总Fig.6 Data summarization ofktc

通过对型钢混凝土框架节点试验结果的研究发现，节点初裂阶段，取ktc=1.2。本文考虑到预应力的有效作用，二级抗裂时取ktc=1.0，三级抗裂时取ktc=1.1。现已获得初裂、屈服极限时的ktc取值，可以计算节点承载力关于节点剪切应变的全过程变化关系。文献[8]中认为节点达到受剪承载力极限时，可取γxy=1.2%。利用MATLAB 软件求解方程后，把混凝土、箍筋、腹板三部分承载力相加就得到了预应力混凝土梁-型钢混凝土柱的节点受剪承载力。

3 承载力计算值与试验值的比较

在梁柱节点试验中，试件不一定发生节点剪切破坏，也可能在梁端发生破坏。由于文中给出的节点承载力计算公式是基于节点剪切应变的，通过绘制承载力与剪切应变关系曲线，可以获得不同破坏形式的节点受剪承载力。此处将针对“梁端弯曲破坏”和“节点剪切破坏”两种节点破坏形式的承载力进行说明。

3.1 “梁端破坏”的承载力说明

在本课题组进行的预应力混凝土梁-型钢混凝土柱框架节点试验(如图7)中，两个框架节点试件的设计参数如表1 所示，型钢混凝土柱截面尺寸及纵筋配筋率、配钢率、配箍率相同；预应力混凝土梁截面尺寸相同，预应力度相同(λ=0.65)，预应力筋用量不同。加载装置如图8 所示。混凝土28 d 棱柱体抗压强度为40.2 MPa。梁柱纵筋采用HRB400 级钢筋，梁柱箍筋采用HPB300 级钢筋，柱中型钢采用Q345 级钢材焊接形成，钢材和钢筋的力学性能指标测定结果如表2 所示。

表1 节点试件参数Table 1 Design parameters of specimens

表2 钢材拉伸试验强度Table 2 Steel strength of tensile test

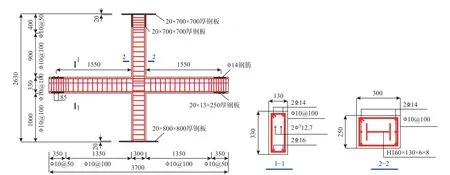
图7 节点尺寸及配筋图 /mmFig.7 Size and reinforcement of specimens

图8 加载装置Fig.8 Loading device

节点YSJ1 的承载力为562 kN，对应的节点剪切应变约为0.0036 rad；节点YSJ2 的承载力为462 kN，对应的节点剪切应变约为0.0028 rad。两个节点均发生梁端弯曲破坏，节点箍筋未屈服。节点YSJ1 和YSJ2 的承载力计算如图9 所示，YSJ1在节点剪切变形为0.0036 rad 时，节点总承载力计算值为551 kN，其中混凝土提供的承载力为408 kN，占74%的比例；型钢腹板提供的承载力为94 kN，占17%的比例；箍筋提供的承载力为49 kN，占9%的比例。与试验值562 kN 相比，误差为2%。

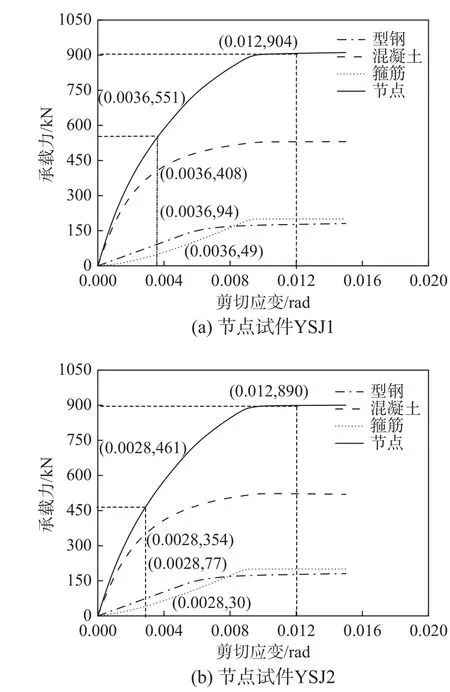
图9 节点受剪承载力计算值Fig.9 Calculated shear strength of joints

根据提出的理论模型，若节点核心区发生破坏时，即认为节点剪切应变达0.012 rad，节点受剪承载力为904 kN。YSJ2 在节点剪切变形为0.0028 rad时，节点总承载力计算值为461 kN，其中混凝土提供的承载力为354 kN，占77%的比例；型钢腹板提供的承载力为77 kN，占17%的比例；箍筋提供的承载力为30 kN，占6%的比例。与试验值466 kN 相比，误差小于1%。若节点核心区发生破坏时，即认为节点剪切应变达到0.012 rad 时，节点受剪承载力为890 kN。提出的模型可较好的计算预应力混凝土梁-型钢混凝土柱节点的受剪承载力。

3.2 “节点剪切破坏”承载力说明

当节点发生破坏时，计算曲线的峰值或剪切应变为0.012 rad 对应值就是节点核心区的极限承载力。此时混凝土承载力达峰值，箍筋、型钢都进入了屈服状态。文献[26 - 27]中的型钢混凝土框架节点发生了剪切破坏，用本文模型也可对这些节点试件J3、J4 和J5[26]及SRCJ-1 和SRCJ-2[27]进行计算，得到的结果如图10 所示，将结果整理如表3 所示。从表3 中可以看出，对于发生剪切破坏的节点受剪承载力，本文的模型计算值误差在3.5%以内，计算值与试验值吻合地较好。

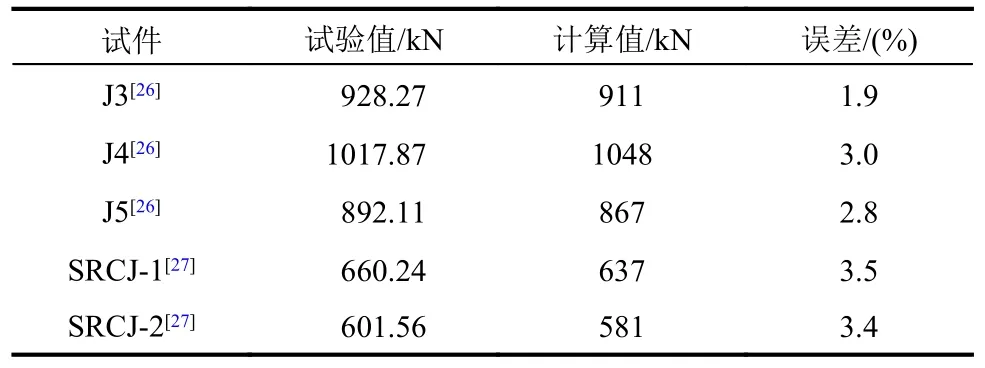
表3 节点承载力计算Table 3 Shear strength calculation

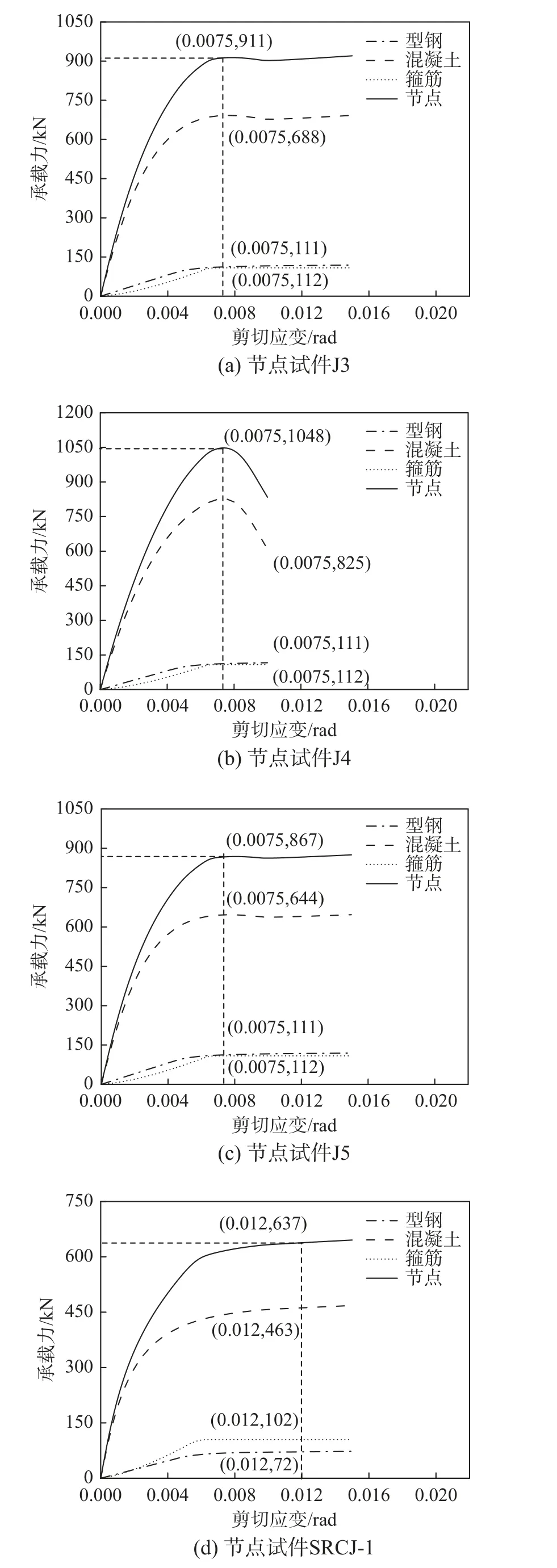
图10 节点受剪承载力计算值Fig.10 Calculated shear strength of joints

4 结论

本文研究了预应力混凝土梁-型钢混凝土柱框架节点中各部分对节点受剪承载力的主要贡献，并在桁架模型与斜压杆模型的基础上，将承载力计算与节点变形分析结合起来，建立了预应力混凝土梁-型钢混凝土柱框架节点受剪承载力计算方法，采用本文试验和文献试验结果验证了所提计算模型的准确性，得到以下主要结论：

(1) 本文提出的节点抗剪模型中，节点受剪承载力的计算由型钢腹板、强约束区混凝土斜压杆和弱约束区混凝土斜压杆三部分叠加组成，并考虑了梁中预应力对受剪承载力的提高作用；通过理论分析，将承载力与节点变形计算结合起来，从而获得节点承载力和节点变形的关系曲线。

(2) 本文提出的节点受剪承载力计算方法，不仅可用于计算发生“节点剪切破坏”的节点试件，也可较为准确地计算发生“梁端弯剪破坏”的节点试件；与本文开展的节点试验和文献试验结果对比可以看出，受剪承载力计算值与试验值的误差在3.5%以内，表明此方法具有较高的精度。

(3) 从受剪承载力-剪切应变曲线可以看出，混凝土是承担节点剪力的最主要部分，承担大部分的节点剪力；而型钢腹板和箍筋是节点剪力承担的重要组成部分，承担比例随着荷载的增加不断增长，直至进入屈服状态。