细聚丙烯纤维混凝土介观离散力学模型及其I 型断裂强度负效应机理

沈 雷，吴 杰，邓通发，曹茂森，徐 磊，李田雨

(1.河海大学水利水电学院，江苏，南京 210024；2.江西理工大学环境岩土与工程灾害控制重点实验室，江西，赣州 341000；3.河海大学工程力学系，江苏，南京 210024；4.滁州学院安徽省桥梁结构数据诊断与智慧运维国际联合研究中心，滁州 239099)

细聚丙烯纤维混凝土(PFRC)在土木工程中运用广泛。细聚丙烯纤维能够预防、减少浇筑期裂缝的萌发与扩展。在混凝土抗火方面，细聚丙烯纤维的添加能够有效抑制孔隙压力的形成，防止高温爆裂现象发生。然而，在介观尺度上(介于宏观与细观之间)，细纤维混凝土力学性能数值研究存在困难。

在模拟方法方面，纤维混凝土力学模型可分为宏观均质化[1-4]，细观计算[5-6]以及介于前两者之间的独立网格法[7]。独立网格法的基本思想是，混凝土基体离散过程与纤维分布相互独立，依据空间关系确定纤维连接的基体单元，当基体出现开裂时桥接作用力计入单元总力。此类方法既消除了纤维对基体离散过程的困扰，又能够模拟各向异性纤维的力学作用，其中混凝土基体的方法有传统有限元[7-8]、无网格法[9]以及本文所用的离散格构模型[10-11]等。然而，对于直径≤100 μm 的细纤维，由于细纤维数量过多，现有模型在刻画数量过多的纤维桥接力以及纤维拔出、断裂过程中需要巨大计算成本。

在物理现象方面，细与粗聚丙烯纤维对混凝土宏观力学性能的作用差异甚大，粗纤维能够显著提升抗弯荷载峰值而细纤维的作用并不明显[12]。诸多试验发现，细聚丙烯纤维的添加会导致混凝土抗拉和抗压强度降低[13-14]。细聚丙烯纤维体积含量在0%～0.3%时，混凝土劈拉强度呈现先增后减的趋势[15]。在纤维体积含量为1%和2%时，三点弯峰值荷载分别下降7.3%和36.0%[16]。可见，细聚丙烯纤维对材料结构以及力学性能的作用并不是单纯的提升作用，其作用机理尚不明晰。

针对现有数值方法的困难和物理认知的不足，本文在钢纤维混凝土力学本构[11,17]的基础上，提出细纤维直径等效概念，并对本构做相应改进，以实现细纤维(直径≤100 μm)混凝土力学行为的模拟，并揭示细聚丙烯纤维含量对混凝土宏观I 型断裂强度的影响。

1 细纤维加强混凝土力学模型

1.1 离散过程

Lattice Discrete Particle Model (LDPM)是介观尺度混凝土离散力学模型，旨在不单独划分骨料和砂浆单元的情况下模拟混凝土非均质材料的破坏行为。假设骨料为球状，在试件内部随机投放骨料，依据配合比确定最大和最小骨料直径(分别为da和d0)，尺寸分布满足Fuller 曲线分布，试件表面投放无体积节点。离散化过程见图1。利用试件表面点和内部骨料球心生成四面体网格，四面体单元的边即为格构单元(Lattice)。取一个四面体单元，有骨料球心Pi和单元中心点T，面中心点Fk以及边中心点Eij为顶点(i,j,k=1,2,3,4 且i≠j≠k)，可在四面体单元中生成12 个三角形潜在开裂面(Facet)。每个Facet 局部坐标系法向单位向量n和切向单位向量m和l。形成由Facet 包裹的多面体胞元(Cell)系统，每个胞元含有一个骨料和周围砂浆。

图1 纤维加强混凝土离散化过程Fig.1 Discretize process of fiber reinforced concrete

1.2 混凝土基体本构

以相邻骨料Pi和Pj之间的潜在开裂面(Facet)为例，如图1。Facet 上应变定义为：

式中：eN为法向应变分量；eM和eL分别为相互正交的切向应变分量； [[u]]为Facet 上的位移间断；l为骨料球心间距；n、m和l分别为相互正交的法向、切向单位向量。

在Facet 上定义法向和切向应力，其弹性的力学响应定义为：

式中：tN为法向应力分量；tM和tL为切向应变分量；相应的EN=E0和ET=αE0分别为法向和切向弹性模量，其中E0=E/(1-2ν)为等效弹性模量；α=(1-4ν)/(1+ν) 为法向和切向的耦合系数，E为弹性模量，ν为泊松比，通常混凝土 α =0.25。

式中：rst=σs/σt为介观剪切强度 σs和介观拉伸强度 σt的比值，须注意模型中的介观强度由校正计算确定；Df表征纤维掺加引起的基体强度上升，随着纤维含量(Vf)增加，纤维界面吸附水分导致局部水灰比降低并且孔隙结构改善[18]，砂浆强度随之增加：

应力峰值后的软化阶段，等效软化模量采用指数函数形式，H0(ω)=Ht(2ω/π)nt，Ht为软化模量，nt=0.2为软化指数。纯拉伸应力状态下，H0(π/2)=Ht=2E0/(lt/l-1) ，其 中：为拉伸特征长度；Gt为脆性断裂能。纯剪切情况下，有H0(0)=0。更多关于高围压状态下的材料密实和孔隙塌陷行为以及压剪状态下的内摩擦行为，请见文献[17]。

Facet 总开裂宽度定义为δ =δNn+δLl+δMm，其中δN=l(eN-tN/EN) 为法向开裂宽度，δL=l(eLtL/EL) 和δM=l(eM-tM/EM)为切向开裂宽度。当混凝土基体发生开裂时，纤维将阻碍缝面间的扩展，在LDPM 中体现为在潜在开裂面(Facet)上的桥接作用力(crack-bringing force)。Facet 的总应力张量则由混凝土基体应力张量(t)和所有相交纤维的桥接总力组成：

式中，Ak为Facet 的面积。当Facet处于压缩状态或开裂宽度为0时，纤维对Facet无应力贡献，Pf≈0；当 δ>0 ，利用开裂宽度计算桥接作用力Pf(δ)。模型中，纤维的加入引入桥接力，同时也减少了水泥基体的粘结面积，当纤维弹模或强度低于水泥基体时，纤维含量的增加会引起混凝土宏观强度的降低，此为负作用机理。

最终，每个由Facet 构成的多面体胞元(Cell)满足力平衡和动量守恒，建立控制方程：

式中： FI为CellI周围的Facet 集合；矢量c为骨料球心指向Facet 的距离；VI为CellI的体积；b为集合 FI中Facet 上的外力集合。

1.3 纤维-基体相互作用

本文以模型计算极限为依据，划分直径≤100 μm为细纤维。而LDPM 的Facet 为介观尺度(>1000 μm)，因此在细纤维和基体力学模型之间存在尺度上的失配。具体反映为，体积含量为0.2%的150 mm×150 mm×150 mm 试件内含有细聚丙烯纤维(df=50 μm，Lf=12 mm)约22.5 万根，可见足尺寸构件模拟的计算成本极高。因此，本节在SCHAUFFERT等[11]、SHEN 等[17]、冯君等[19]工作基础上引入纤维直径等效系数rf=/df≥1，在不影响模型精度的同时降低纤维投放数量(=Nf/rf2)，以提升模型计算效率，使其能够模拟细纤维(df≤100 μm)加强混凝土力学行为。

假设纤维垂直于裂缝面(图2)，纤维从混凝土基体中拔出主要分为如下阶段：第一阶段，纤维与基体胶结绑定，当基体内裂缝萌发，纤维阻碍裂缝面张开而受力，纤维与基体胶结面产生剪切应力；第二阶段，随着荷载的增大，纤维和基体开始脱粘，此时为局部绑定状态，纤维并未与基体发生较大滑移，纤维和基体间的绑定能(Gd)抵消纤维桥接力做功；第三阶段，当纤维和基体完全脱粘，纤维被桥接力牵引从砂浆中拔出，在拔出过程中纤维与基体壁面发生摩擦(初始摩擦力τf0)；最终，纤维从基体中被完全拔出，在基体中形成一个管状裂缝。

图2 纤维垂直拔出示意图Fig.2 Diagram of pull-out behavior of vertical fiber

上述纤维拔出的不同阶段可表现为桥接力随纤维滑移(ν)变化。纤维滑移值达到临界值(νd)时，认为纤维与基体完全脱离(第三阶段)，该临界值定义为：

在纤维脱粘的过程中(ν<νd)，桥接力做功可分解为纤维与基体绑定能以及纤维与基体摩擦力做功：

当纤维与砂浆完全脱粘(ν>νd)，纤维逐渐被拔出，与管道壁面发生摩擦：

图3 倾斜纤维拔出示意图Fig.3 Illustration of pull-out behavior of slant fiber

上述纤维桥接作用力存在的前提是纤维没有发生断裂。因此，须比较纤维桥接力与纤维极限承载力。当满足式(14)时，认为纤维为断裂。

式中：krup为材料参数； σuf为纤维拉伸强度。

2 试验与模拟概况

为校正和验证所提模型，本文开展纤维体积含量分别为0%、0.1%和0.2%细聚丙烯纤维加强混凝土的预制裂缝三点弯曲梁和立方体单轴压缩实验，配比和编号见表1。原材料为：42.5 级普通硅酸盐水泥；细骨料为细度模数为2.7～3 的天然河砂；粗骨料为粒径3 mm～20 mm 的连续级配碎石；普通自来水；聚羧酸减水剂；细聚丙烯纤维长度为12 mm，平均直径为50 μm。立方体单轴压缩和三点弯曲梁试件尺寸分别为150 mm×150 mm×150 mm和100 mm×100 mm×400 mm，梁预制裂缝深度40 mm，宽度2 mm。常温浇筑，静置24 h 后脱模，标准养护28 d。

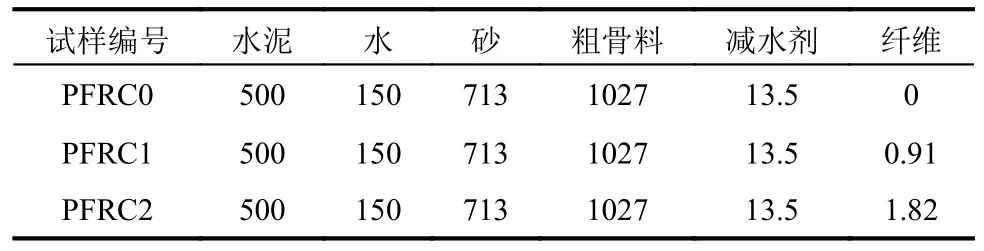
表1 混凝土配比 /(kg·m-3)Table 1 Concrete mixture

图4 为试验装置示意图。立方体单轴压缩试验采用全自动恒应力压力试验机，最大试验力为2000 kN，加载速率为0.3 MPa/s，试件与试验机压板之间无润滑处理。三点弯曲梁试验采用电液伺服试验机，最大试验力为500 kN，跨中位移加载速率为0.3 mm/min。试验过程中，立方体应变、三点弯跨中缝口张开宽度(CMOD)等信息采用由Imetrum 公司提供的视频应变仪。

图4 物理试验与数值模拟示意图 /mmFig.4 Illustrations for experiments and simulations

模拟中采用的数值试件尺寸、骨料尺寸、纤维尺寸和边界条件均与物理试验一致，如图4 所示。计算参数由试验数据校正确定，见表2。立方体数值模拟中，上下刚体与混凝土接触面采用高摩擦系数(μ=0.015+0.1285/s[17])，其中s为接触面节点滑移。三点弯曲梁试验中，为提升计算效率，除跨中200 mm 以外部分采用线弹性有限元计算，其弹模由立方体抗压试验结果确定。

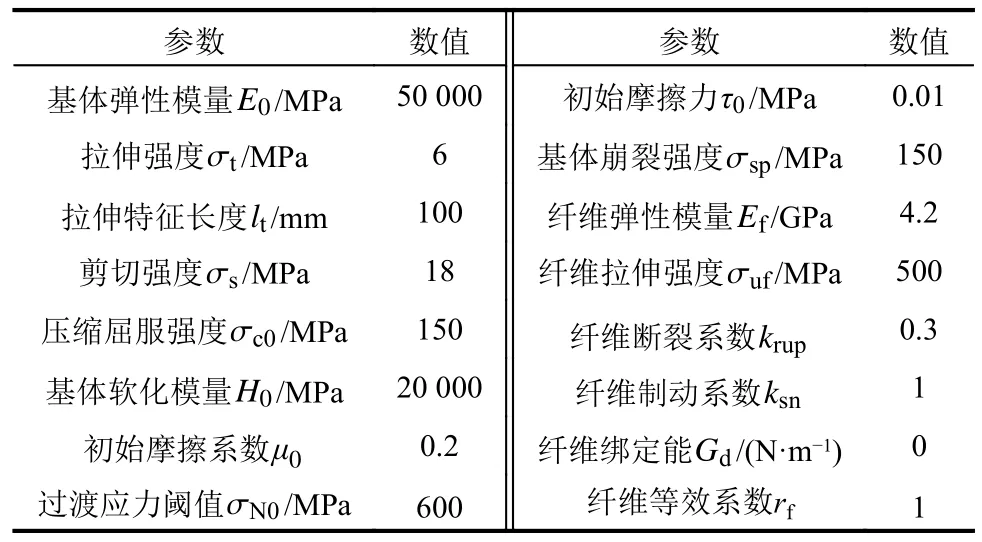
表2 介观力学参数Table 2 Mesoscopic mechanical parameters

3 计算结果

3.1 模型的校准与验证

第一步，校准素混凝土模型参数，见表2 左侧。通过比较三点弯曲梁跨中荷载峰值以及软化段曲线与试验测量数据，确定混凝土介观抗拉强度、特征长度和脆性能释放速率，通过比较立方体单轴压缩宏观弹性模量和抗压强度与试验测量数据，确定混凝土介观弹性模量和剪切强度。图5和图6 分别比较了PFRC 三点弯曲梁和立方体轴压试验和数值结果。图5(a)和图6(a)分别为混凝土基体(PFRC0)三点弯曲梁跨中荷载和CMOD 关系曲线和立方体单轴压缩应力-应变曲线，模拟结果与试验宏观力学响应吻合。

图5 三点弯曲梁试验与数值模拟Fig.5 Simulations of three-point bending tests

图6 单轴压缩试验与数值模拟Fig.6 Simulations of uniaxial compression tests

第二步，校准纤维-基体模型参数，见表2 右侧。通过比较三点弯曲梁跨中荷载峰值以及软化段曲线与试验测量数据，确定纤维初始摩擦力。由图5(b)可见，PFRC1 三点弯曲梁跨中荷载关于CMOD 的模拟曲线与试验数据吻合较好。

第三步，验证模型准确性。使用表2 参数，预测PFRC2 的三点弯曲梁跨中荷载与CMOD 曲线和立方体单轴压缩应力-应变曲线。如图5(c)所示，无论是荷载峰值还是软化段下降规律均与试验测量结果较为吻合。图5(d)为PFRC2 CMOD=0.15 mm时开裂宽度云图以及裂缝扩展路径，与试验结果吻合。试验过程观察发现，断裂面少见混凝土基体碎屑，纤维多见断裂，少见拔出。图6(b)和图6(c)分别为模型预测的PFRC1 和PFRC2 的立方体单轴压缩应力-应变曲线，无论是压缩强度还是宏观弹性模量均与试验测量结果吻合。图6(d)为PFRC2单轴压缩应变为0.01 时开裂宽度分布云图，以及对应试验中试件的破坏形态。

3.2 纤维直径等效系数的验证

理论上，当纤维拔出角度与基体相对位置保持不变时，上述等效方法严格成立。但在实际情况中，混凝土数值试件内骨料和纤维均随机分布，离散后潜在开裂面(Facet)与纤维拔出角度随机，上述等效方法不严格成立。基于代表体积单元体的思想，当纤维数量高于某一个数量级时，随机分布且各向异性纤维桥接作用力对混凝土宏观力学性能的作用是近似的，即统计学层面的等效。因此，本节首先对等效方法的正确性和相关限制条件进行研究和讨论。

以df=0.1 mm，Lf=12 mm，Vf=0.2%为例，rf分别取1、2、5、10、20 和40，其余计算参数见表2。采用完全相同的混凝土数值试件和模拟参数，仅将纤维方向随机生成。如图7 为rf=1、10和20 断裂区域纤维分布，随着rf逐渐增大，纤维数量减少。在rf≤10 时，跨中荷载与CMOD 曲线基本重合，等效方法成立。而在rf>10 时，跨中荷载与CMOD 曲线在峰值处分离，并在软化段出现显著偏差，说明此时rf过大，纤维数量无法保证统计学层面的等效结果。可见，rf=10 为一个合理数值，此时纤维数量可减少100 倍。rf取10 可在保证计算结果与实际相同的情况下，大幅提升计算效率，为结构层面的模拟创造了可能性。

图7 纤维等效系数验证Fig.7 Validations of equivalent coefficient of fiber diameter

3.3 纤维含量的影响

本文以及前人的试验结果均表明，细纤维含量增加会引起混凝土的I 型断裂强度先升后降现象，而此前模型[8,11,17]均无法刻画该现象。对此，模型在式(6)中引入细纤维亲水导致局部水灰比提升引起的基体强度上升，式(7)引入纤维夹杂引起的对Facet 基体有效粘结面积的减小，即Facet 面积 (Ak)分为多根纤维的总面积和混凝土胶结面积。细纤维添加导致混凝土材料结构发生改变，相应地对宏观力学行为造成两种截然不同的影响：其一是正效应，即局部基体水灰比增加引起的强度增加和纤维桥接力作用；其二是负效应，即随着纤维含量的增加，Facet 中混凝土粘结面积减少，导致力学性能下降。钢纤维的添加对混凝土抗拉强度有显著提升[17]，说明正效应占据主导地位。

图8 为三点弯跨中荷载峰值随Vf的变化规律。其中，采用本文表2 介观参数时(τ0=0.01 MPa)，Vf的增加无法提升混凝土抗拉性能。当τ0=0.1 MPa和τ0=0.5 MPa 时，混凝土在Vf分别为0.1%和0.2%处发生正、负效应主导地位转换。可见，随着纤维与基体初始摩擦力(τ0)的提升，从I 型断裂强度的角度，细纤维的最佳体积含量也随之增加。

图8 纤维含量与荷载峰值关系Fig.8 Relation between fiber dosage and load peak

图8 比较了模型预测结果与和实验结果。本文实验结果表明：细聚丙烯纤维体积含量为0.1%和0.2%时，添加纤维导致试件三点弯跨中荷载峰值下降，说明负效应占据主导地位。GUO 等[15]试验结果表面，混凝土的劈拉强度随纤维含量(Vf=0.12%、0.17%和0.22%)呈现先增后减的趋势，相对变化值为+3.3%、+1.7%和-13.3%。BENCARDINO等[16]测得三点弯曲梁峰值荷载随纤维含量(Vf=1%和2%)增加而分别变化-7.3%和-36.5%。

4 结论

本文通过定义纤维等效系数(rf)，提出细聚丙烯纤维(直径≤100 μm)介观离散力学模型，能够模拟纤维随机分布、纤维含量、纤维长度的宏观力学性能的影响，并阐明I 型断裂强度随纤维含量先增后减的力学机理。研究结果表明：

(1) 纤维数量随rf增大而呈平方倍减少，计算效率显著上升。但由于纤维分布的随机性和混凝土基体的非均质性，rf过大导致计算精度降低，建议取rf≤10。

(2) 细PP 纤维微亲水性提升基体局部水灰比为强度正效应，纤维桥接力强度贡献低于砂浆的强度负效应。当纤维微量添加时，细PP 纤维微亲水性提升基体局部水灰比，使基体强度上升，此时正效应高于负效应；随着纤维含量增加，由于纤维桥接力贡献无法补偿相应面积基体强度，强度随负效应持续增长而呈减小趋势。