基于层叠式残差LSTM 网络的桥梁非线性地震响应预测

廖聿宸，张瑞阳，林 榕，宗周红，吴 刚

(1.东南大学混凝土及预应力混凝土结构教育部重点实验室，江苏，南京 211189；2.东南大学智慧建造与运维国家地方联合工程研究中心，江苏，南京 211189；3.东南大学土木工程学院，江苏，南京 211189；4.东南大学爆炸安全防护教育部工程研究中心，江苏，南京 211189)

桥梁作为公路、铁路、市政工程的重要交通基础设施，保障其运营安全对国家社会经济发展具有重要意义。特别是，桥梁面临强震、重载、飓风、海啸等各类极端事件威胁[1]，如何快速、准确地评价桥梁的抗灾变能力成为亟待解决的难题。通常，采用弹塑性有限元分析方法预测桥梁遭受极端荷载时的结构响应[2-6]。然而，非线性有限元分析存在计算耗时长、实时性差等问题。诸如桥梁易损性分析[7-9]、可靠度分析[10]以及非线性模型修正[11]等方法需重复若干次有限元分析，加剧了原本高昂的计算成本。因此，亟需发展耗时少、精度高的高效代理模型，实现桥梁性能的快速评估。

为建立桥梁响应与荷载作用的近似映射关系，降低结构分析的计算成本，多元回归模型[12]、Kriging 模型[13-14]、径向基函数(radius base function,RBF)[15]、ARMA 模型[16]、支持向量机(support vector machine, SVM)[17]等代理模型已得到广泛应用。但是上述代理模型拟合参数少，通常只适用于线性或弱非线性系统的动力响应预测，难以揭示大变形情况下复杂系统的动力性能[18]。相比之下，人工神经网络(artificial neural network, ANN)具备较为优良的非线性拟合能力，成为非线性动力系统建模的强力工具[19]。例如，JENG 等[20]通过多层感知机(multilayer perceptron, MLP)预测了预应力混凝土简支梁桥的结构响应，并比较了不同网络层数、隐藏层节点数目等超参数对预测精度的影响。WANG 等[21]建立了4 层ANN 模型来预测预应力混凝土刚构桥的地震响应，并采用Levenberg-Marquardt 算法进行网络训练，实现了中小震下桥梁响应的准确预测。ABBAS 等[22]采用ANN 模型建立了桥梁典型气动力响应与自激气动力之间的关系，为桥梁气动外形设计提供更为便捷的计算工具。

虽然ANN 模型已在非线性响应建模方面取得不少成果，但是其浅层网络结构使得复杂非线性动力系统的响应预测仍存在精度不足的问题。目前深度学习已经有了迅猛发展，深度神经网络(deep neural network, DNN)为克服上述问题提供了更为有效的思路。WU 和JAHANSHAHI[23]将卷积神经网络(convolution neural network, CNN)模型应用于单自由度与多自由度结构的动力响应预测，分析了预测值与真实值的误差分布、频谱差异。然而，CNN 模型更多地关注时间序列的局部特征，无法有效捕捉相邻时刻的相关关系。相比而言，循环神经网络(recurrent neural network, RNN)及长短时记忆神经网络(long short-term memory neural network, LSTM)等变体网络在序列预测方面具有良好的优势，部分研究人员成功将其应用于非线性动力系统的响应预测。PEREZ-RAMIREZ等[24]借助RNN 模型预测大型结构的地震响应，并采用Bayesian 正则化方法对网络参数进行优化训练。ZHANG 等[25]通过双层LSTM 网络对多层框架结构的地震响应进行准确预测，同时提出层叠式LSTM 网络(LSTM-s)降低网络规模以提高训练效率。随后，ZHANG 等[26]进一步将物理信息嵌入多层LSTM 网络的损失函数，有效改善了少样本下的非线性地震响应预测精度。TORKY 等[27]采用一种混合ConvLSTM 网络(convolution-long short-term memory neural network)对高层建筑在三向地震动输入下的结构响应进行预测，充分发挥LSTM 网络的复杂序列回归能力与CNN 网络的多维信息捕捉能力。许泽坤和陈隽[28]提出了一种单向多层堆叠式的LSTM 网络，通过滑动时间窗实现了非线性结构地震响应的递推计算。LI 等[29-30]提出了数据驱动的LSTM 网络和物理信息嵌入的RNN 网络，利用监测数据成功预测出大跨度悬索桥的抖振和涡激振动响应。RAO 等[31]将控制方程、边界条件、初值条件等约束作为物理信息引入神经网络，实现了无标签数据的弹性动力问题建模。

目前，基于深度神经网络的桥梁非线性地震响应建模仍较少见，相关研究的预测效果也有待改善。在已有研究的基础上，本研究结合残差网络结构与LSTM 网络的优势，提出一种数据驱动的层叠式残差长短时记忆神经网络(residual long short-term memory neural network, ResLSTM)作为代理模型，改善经典深度LSTM 网络的预测效果，并首次应用于地震作用下的桥梁非线性响应预测。最后，通过预应力混凝土连续梁桥与组合梁斜拉桥两组数值算例，以及美国Meloland 跨线桥的现场监测数据进行验证，并依据相关系数、峰值响应误差等指标对模型的非线性响应预测性能进行检验。

1 层叠式残差长短时记忆网络

1.1 残差长短时记忆网络结构

采用图1 的ResLSTM 神经网络构建桥梁地震响应的代理模型，该模型对应于桥梁结构的真实物理模型或数值模型。ResLSTM 网络的输入为地震动的加速度时程，而输出为结构位移、速度、加速度等地震响应时程。所提出的网络单向堆叠了输入层、两层LSTM 层和两层全连接层(fullyconnected layer，FC)，以及输出层，由此形成层叠式的LSTM 网络。进一步地，在LSTM 网络中引入残差连接模块(residual connection，RC)，形成层叠式残差神经网络(ResLSTM)。RC 模块源自HE 等[32]提出的残差神经网络(residual neural network，ResNet)，已在语义分割[33]、情感分析[34]等场景广泛应用。RC 模块能够缓解误差反向传播、修正时的梯度消失现象，使得LSTM 等DNN的优化训练更为容易、稳健；同时，上一隐藏层输出的细节信息在前向计算过程中得以完好保留。因此，RC 模块能最大程度地保证DNN 的预测精度和鲁棒性。

图1 ResLSTM 网络结构Fig.1 The structure of ResLSTM neural network

ResLSTM 中，RC 模块将相邻两层LSTM 层的输出进行逐元素相加，具体实现方式如下：

式中：yRC为RC 模块的输出；yLSTM1和yLSTM2分别为第一层和第二层LSTM 层的输出； HLSTM2(·)为第二层LSTM 层的非线性映射， ReLU(·)为线性整流函数。进一步地，RC 模块的输出结果传入FC 层，并由两层FC 层映射为桥梁的地震响应。

ResLSTM 网络中，LSTM 层由若干LSTM 单元组成，其层数经试算确定为两层。LSTM 单元如图2 所示，包含输入门it、遗忘门ft、tanh 层及输出门ot，单元中各激活函数及计算流程如式(3)～式(8)所示。LSTM 单元通过门机制决定当前时刻输入xt与上一LSTM 单元输出ht-1的信息保留程度，实现长短期信息的筛选与保留[35]。

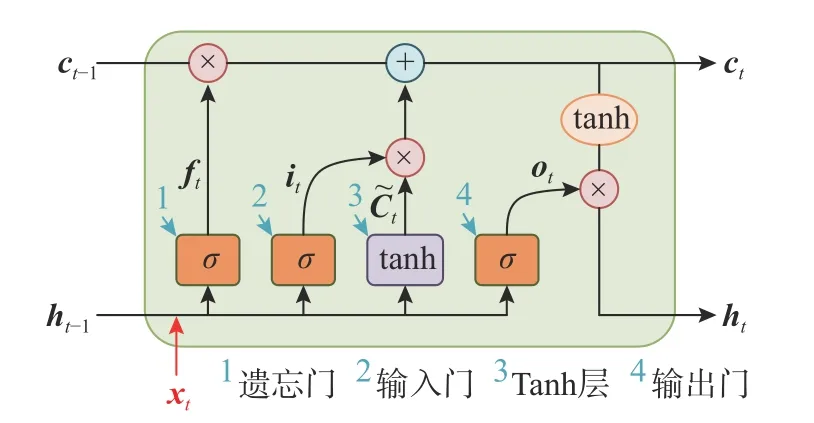
图2 LSTM 单元结构Fig.2 The structure of the LSTM cell

图3 输入与输出序列划分Fig.3 Division of input and output sequences

式中： σ(·) 为 sigmoid 函数； tanh(·)为双曲正切函数；Wp(p=f,i,o)为输入门、遗忘门、输出门的权重矩阵；bp(p=f,i,o)为输入门、遗忘门、输出门的偏置向量； ⊗为矩阵或向量之间逐元素相乘。

ResLSTM 网络采用均方误差(MSE)作为损失函数，具体形式如下：

式中：J为损失函数；D={(xi,yi)|i=1,2,···,Nm}为训练集数据；xi和yi分别为第i组训练样本的输入序列和输出序列；Nm为训练集样本数量；Hi(w,b,x)为给定参数和输入的网络预测结果。

ResLSTM 网络的优化目标如式(10)所示，采用Adam 优化算法[36]对网络进行训练。此外，采取剪枝操作(dropout)防止网络过拟合[37]，节点随机失效概率设置为0.2。

1.2 层叠式序列结构

为减少LSTM 隐藏层节点数量，将地震动记录构成的输入序列X=[x1,x2,···,xn]T∈Rn×Ni和地震响 应 构 成 的 输 出 序 列Y=[y1,y2,···,yn]T∈Rn×No按照固定窗长sw划分为若干段子序列(Ni和No分别表示输入与输出的特征数量)。由此，进一步降低ResLSTM 网络的训练难度和耗时，并提高地震响应的预测精度。

2 数值算例验证

2.1 双跨连续梁桥地震响应建模

通过文献[38]的Benchmark 模型验证方法效果。原桥为两跨预应力混凝土连续梁桥，主梁与盖梁、盖梁与桥墩均为固结。其中，主梁梁高为2.36 m，盖梁高3.2 m，桥墩高7.32 m，墩身最大外径为2.73 m。采用ABAQUS 软件建立有限元模型，模型如图4 所示，全桥模型共计430 个自由度。其中，主梁、盖梁、桥墩采用B31 单元进行模拟，端横梁采用刚体单元模拟，支座通过非线性弹簧单元模拟，桥台、桩基的土-结构相互作用通过线性弹簧-阻尼单元模拟。此外，为提高计算效率，桥墩依据受力情况分为弹塑性区段和弹性区段。其中，弹塑性区段采用了双折线模型来描述桥墩的弯矩-曲率关系，从而模拟桥墩在地震作用下的非线性行为。

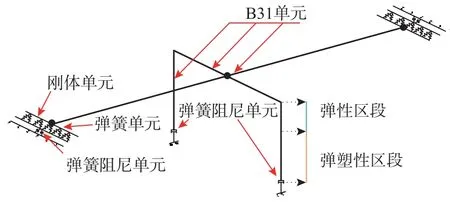
图4 Benchmark 模型[38]Fig.4 The benchmark model

将ABAQUS 模型的质量矩阵、单元刚度矩阵以及单元切线刚度矩阵导入MATLAB，并基于Rayleigh 阻尼假定生成结构阻尼矩阵，阻尼比取5%。采用MATLAB 的ODE45 求解器进行弹塑性时程分析，计算过程根据材料本构和构件应力状态对总体刚度矩阵进行迭代更新；地震加速度输入方向垂直于主梁轴线方向，分析步长为0.005 s，输出步长为0.01 s。从美国NGA 数据库[39]的100 条强震记录中选取12 条进行增量动力分析，按照原始记录的0.6 倍、0.7 倍……1.5 倍进行调幅。当地震位移响应超过0.08 m 时桥梁结构因塑性变形过大已发生破坏，因此剔除峰值位移大于0.08 m的地震响应计算结果，避免过大非线性对模型训练的不良影响。之后，从各组结果中选取5 条响应时程作为训练集与验证集样本，共计60 个样本。除上述12 条地震动记录以外，另随机选取20 条地震动记录，按照0.1 倍、0.2 倍……1.5 倍幅值进行弹塑性时程分析，所得计算结果作为预测集，共计300 个样本。

基于Python 环境的Pytorch 框架训练深度神经网络，计算机配置为8 核16 线程i7-10900 CPU和NIVIDIA ROG-RTX3060 GPU。时间序列的划分窗长为10，LSTM 层节点数量为50，训练过程的最大迭代步数为50 000，L2 范数正则化系数为1×10-8，初始学习率为0.001，批训练样本数为20。训练前，将全部数据归一化至[-1,1]的闭区间上，以此消除量纲差异，加快网络优化的收敛速度。同时，采用文献[25]的LSTM 网络进行对比，并选取相同的训练样本、划分窗长、优化器、最大训练步数，以及LSTM 的隐藏层节点数目。

本研究通过相关系数和峰值响应的相对误差来衡量模型的预测精度。其中，相关系数是回归分析的常用无量纲指标，可以衡量序列间的整体相似度，并消除序列幅值差异对评价结果的影响。相关系数的定义如下式所示：

式中：CI(Ypre,Yref) 为 预测响应Ypre和目标响应Yref之间的相关系数； Cov(·)为不同序列间的协方差；Var(·)为序列的方差。

因相关系数仅反映地震响应预测值与目标值的整体相似度，未能考虑峰值响应对结构的重要影响。因此，另采用峰值响应的相对误差对模型预测精度进行补充评价：

式中：Epr为相对误差； |Ypre,p| 和 |Yref,p|分别为峰值响应预测值和目标值的绝对值。在后续分析中，相关系数与峰值响应相对误差两类评价指标的集中程度将通过四分位值进行量化。评价指标分布越集中，说明模型的预测精度越稳定、鲁棒性越好。

图5 分别给出了两类网络预测结果的评价指标分布情况，并标出了4 组典型工况的评价指标；表1 列出了评价指标的统计结果。相比LSTM 网络，ResLSTM 预测结果的相关系数分布更为集中。其中，ResLSTM 网络的上四分位数和下四分位点分别为0.9116 和0.9320，而LSTM 网络的上四分位数和下四分位数分别为0.9088 和0.9318。由此表明，ResLSTM 网络的鲁棒性强于LSTM 网络。对比最小相关系数，LSTM 网络为0.7571，ResLSTM 网络则为0.7336。虽然ResLSTM网络的最小相关系数更低，但是仅个别测试集样本的预测结果出现偏差，而LSTM 网络在较多测试集样本上存在明显预测误差。因此，上述结果表明ResLSTM 网络的预测精度总体良好，相较于LSTM 网络表现出更好的鲁棒性，仅在个别样本上表现欠佳。通过查验测试集数据，预测偏差大的样本均来自同一组地震动记录的增量分析结果，且两类模型均无法准确预测所提及的几组地震响应。如图6 所示，其原因在于，该组地震动与训练集的地震动在末尾段的振动规律存在较大差异，使得该范围内响应预测值与目标值发生偏离。

表1 评价指标统计结果(梁桥)Table 1 The statistics of the assessment indicators (the girder bridge)

图5 评价指标分布(梁桥)Fig.5 Distribution of assessment indicators(the girder bridge)

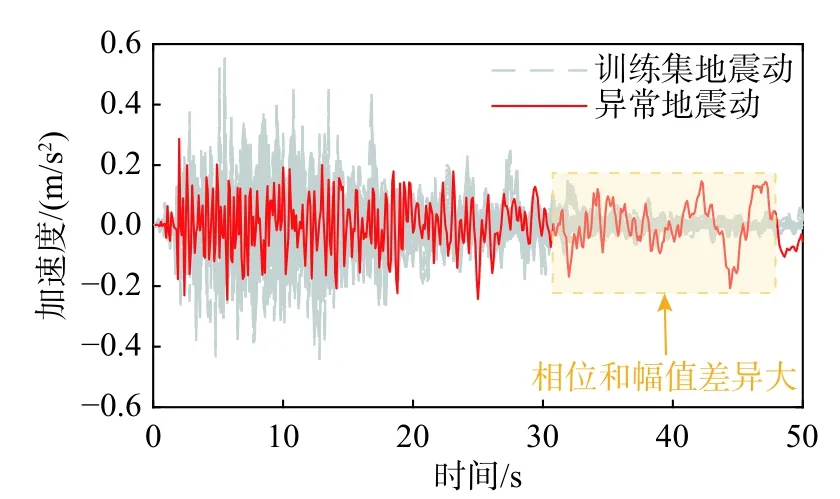
图6 训练集样本与预测异常样本的地震动对比Fig.6 Comparison between the ground motions of the training samples and the abnormal prediction sample

峰值响应的相对误差也验证了ResLSTM 模型具有良好的预测性能。对于ResLSTM 模型，峰值响应预测误差的四分位数分别为-3.23%和1.13%；对于LSTM 模型，四分位数则为-3.61%和3.60%。此外，ResLSTM 模型预测误差的最大值和最小值分别为6.94%和-15.59%，LSTM 模型则为19.15%和-28.28%。上述研究结果表明，ResLSTM 模型对峰值响应的预测较LSTM 模型更为可靠，预测精度总体更为准确。

图7 给出了图5 中4 组典型地震作用工况下主梁跨中横向位移(垂直于桥轴方向)的预测结果。对于数值算例，图上目标值代表有限元仿真结果。可以看出，在线性与弱非线性情况下(图7(a)和图7(b))，ResLSTM 网络准确预测了跨中位移，而LSTM 网络存在轻微偏移；在强非线性情况下(图7(c)和图7(d))，两者预测结果的相位与目标值一致，仅部分时段幅值产生偏离，且ResLSTM 网络较LSTM网络偏差更小。此外，ResLSTM 网络平均计算耗时0.017 s，LSTM 网络平均计算耗时0.011 s，有限元分析耗时约24.125 s。需指出，该有限元模型较为简单，并通过matlab 环境进行优化，因而计算效率较高。相比之下，ResLSTM 网络和LSTM网络的耗时仅为有限元模型的0.71‰和0.435‰。因ResLSTM 网络采用残差结构，其计算效率略低于LSTM 网络。但是，两者计算耗时仅相差0.0067 s，并远高于有限元方法，证明了ResLSTM 网络的高效性。

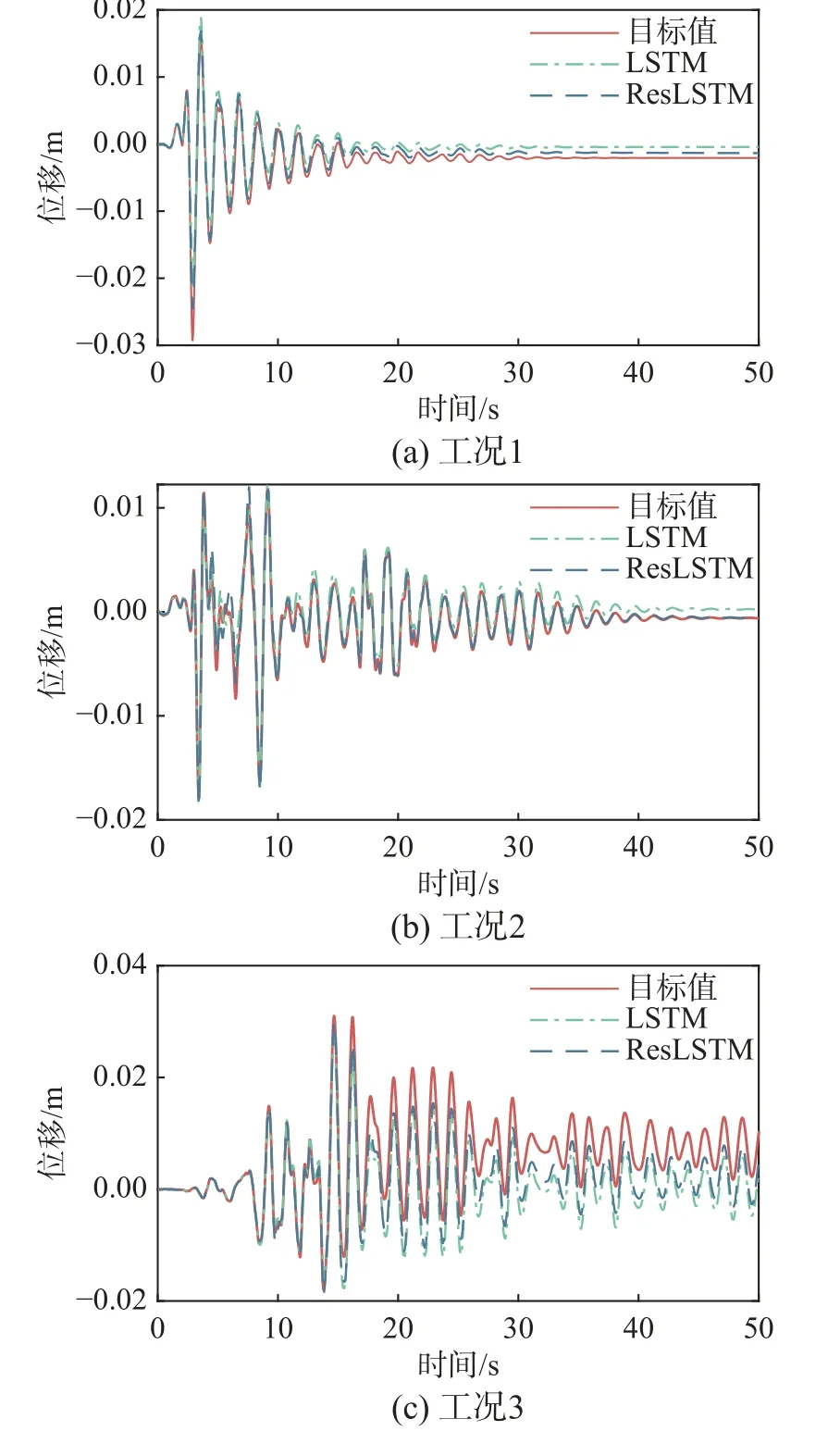
图7 主梁跨中横向位移时程对比Fig.7 Comparison of transverse displacement time histories at the mid-span of the girder

2.2 组合梁斜拉桥地震响应建模

借助文献[40]的斜拉桥OpenSees 模型进一步验证本方法对大跨度桥梁的适用性，模型如图8所示。原桥为沿海高速(G2)灌河特大桥，属于半漂浮体系斜拉桥，跨径布置为(32.9+115.4+340+115.4+32.9) m。大桥主梁采用预应力混凝土-I 形钢梁组合梁，主梁高度为3.08 m，桥面宽度为36.6 m；桥塔采用钢筋混凝土空腹式截面，塔高119.629 m(自基础顶面以上)。因半漂浮体系斜拉桥在地震作用下的塑性铰通常位于桥塔与桥墩，仅采用forceBeamColumn 单元模拟上述构件的弹塑性行为，其余构件采用弹性单元。模型的材料特性、边界条件等参数已采用环境振动试验进行修正[40]。

图8 灌河大桥OpenSees 模型Fig.8 The OpenSees model of Guanhe bridge

同2.1 节，选取相同地震动记录进行增量动力分析，加速度输入的幅值依次取0.6 倍、0.7 倍……1.5 倍的原始幅值。基于Rayleigh 阻尼假定生成结构阻尼矩阵，阻尼比取5%；地震加速度输入方向平行于主梁轴线方向，分析步步长与输出步长均为0.02 s。采用相同计算平台和深度学习框架进行深度神经网络的训练，并从15 组计算结果各选取4 条响应时程作为训练集与验证集样本，共计60 个样本。除上述15 条地震动记录以外，另随机选取30 条地震动记录的增量动力分析结果作为预测集样本，共计300 个测试样本。因加速度输入和结构响应的采样频率与2.1 节不同，时间序列的划分窗长设置为5；同时，考虑到斜拉桥响应的复杂性，LSTM 隐藏层节点数量设为100，训练过程的最大迭代步数为60 000。除上述参数以外，其余参数与数据预处理方法与2.1 节相同。

图9 给出了塔顶位置纵向位移预测结果的指标分布，并在表2 中列出了指标的统计结果。同时，图上标注了两组典型工况的评价指标，对应的响应时程见图10。与连续梁桥预测结果类似，ResLSTM 网络预测结果的相关系数分布更为集中。根据统计结果，ResLSTM 网络的上四分位点和下四分位点分别为0.8613 和0.8897，而LSTM网络的上四分位点和下四分位点分别为0.8613 和0.8783。对比最小相关系数，LSTM 网络为0.6743，ResLSTM 网络则为0.6558。与梁桥地震响应预测相同，相关系数最小的预测结果来源同一组预测样本，由同一地震动记录生成。由此可知，ResLSTM网络在预测大跨度斜拉桥的非线性地震响应时仍表现出更为良好的鲁棒性，其预测效果较LSTM网络更为稳定。

表2 评价指标统计结果(斜拉桥)Table 2 The statistics of the assessment indicators (the cable-stayed bridge)

图9 评价指标分布(斜拉桥)Fig.9 Distribution of assessment indicators(the cable-stayed bridge)

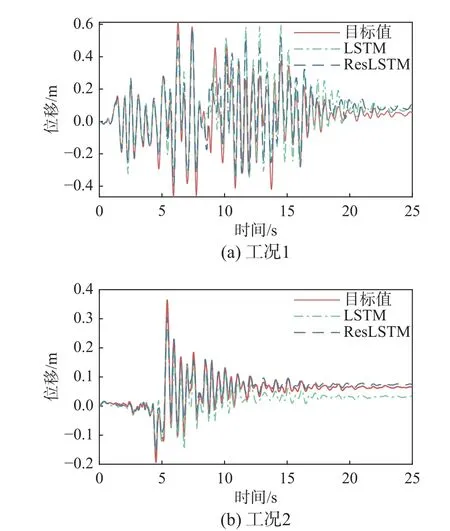
图10 桥塔塔顶纵向位移时程对比Fig.10 Comparison of longitudinal displacement time histories at the top of the tower

类似地，峰值响应的相对误差也表明ResLSTM网络在预测斜拉桥峰值响应时具有更好的预测性能。由结果可知，ResLSTM 网络预测误差的最大值和最小值分别为25.65%和-27.12%，优于LSTM 网络。同时，ResLSTM 网络预测误差的中位数为-3.40%，上四分位数和下四分位数分别为-10.11%和5.62%。相比而言，LSTM 网络的误差中位数为-8.00%，上四分位数和下四分位数分别为-13.16%和-0.41%。可见，ResLSTM 网络的预测误差关于零值对称分布，且误差中位数的绝对值小于5%。而LSTM 网络的预测误差主要分布在-13.16%～-0.41%，且误差中位数的绝对值大于5%，说明预测的峰值响应总体上小于实际峰值响应，预测结果偏于危险。

图10 对比了塔顶纵向位移时程的预测结果，图上的目标值代表有限元分析得到的塔顶位移时程。可以看出，相比于经典的LSTM 网络，ResLSTM网络所预测的峰值响应、残余位移更贴近真实位移响应。因此，对于结构形式更为复杂的大跨度斜拉桥，ResLSTM 网络依旧能够较为准确地预测其非线性地震响应，表现出良好的预测性能。进一步地，分析代理模型和有限元模型的计算效率，ResLSTM 网络平均耗时为0.01195 s，LSTM模型平均耗时0.00892 s，有限元分析平均耗时约10 min。由此可知，ResLSTM 网络的计算效率仍与LSTM 网络相当。不仅如此，因斜拉桥有限元模型的自由度较梁桥大幅增加，其计算耗时远高于ResLSTM 网络和LSTM 网络。相较而言，ResLSTM 网络和LSTM 网络的耗时仅为有限元模型的0.020‰和0.015‰。与2.1 节结果对比，随着桥梁模型复杂度的提高，ResLSTM 网络计算时间基本一致，而有限元模型计算成本明显增加。上述对比证明，在保证精度的前提下，ResLSTM网络具有令人满意的计算效率。

2.3 鲁棒性检验

因ResLSTM 网络属于数据驱动的代理模型方法，其预测效果受到训练集样本的影响。当训练集包含噪声污染的样本时，神经网络的预测性能可能下降。为此，以2.1 节中的连续梁桥数值算例为例(斜拉桥算例结果类似)，从训练集中随机抽取10%、20%、30%的样本混入高斯白噪声，样本输入(加速度)和输出(位移)的信噪比分别为15 dB 和50 dB；测试集的样本保持不变，不添加高斯白噪声。由此，分析含噪声样本占比对ResLSTM网络预测效果的影响。

图11 给出了不同噪声样本比例下的ResLSTM网络预测指标。可以看出，随着含噪样本的比例增加，ResLSTM 网络的预测性能未出现显著下降。而且在含噪样本比例达30%的情况下，ResLSTM仍旧能较为准确地预测非线性地震响应。

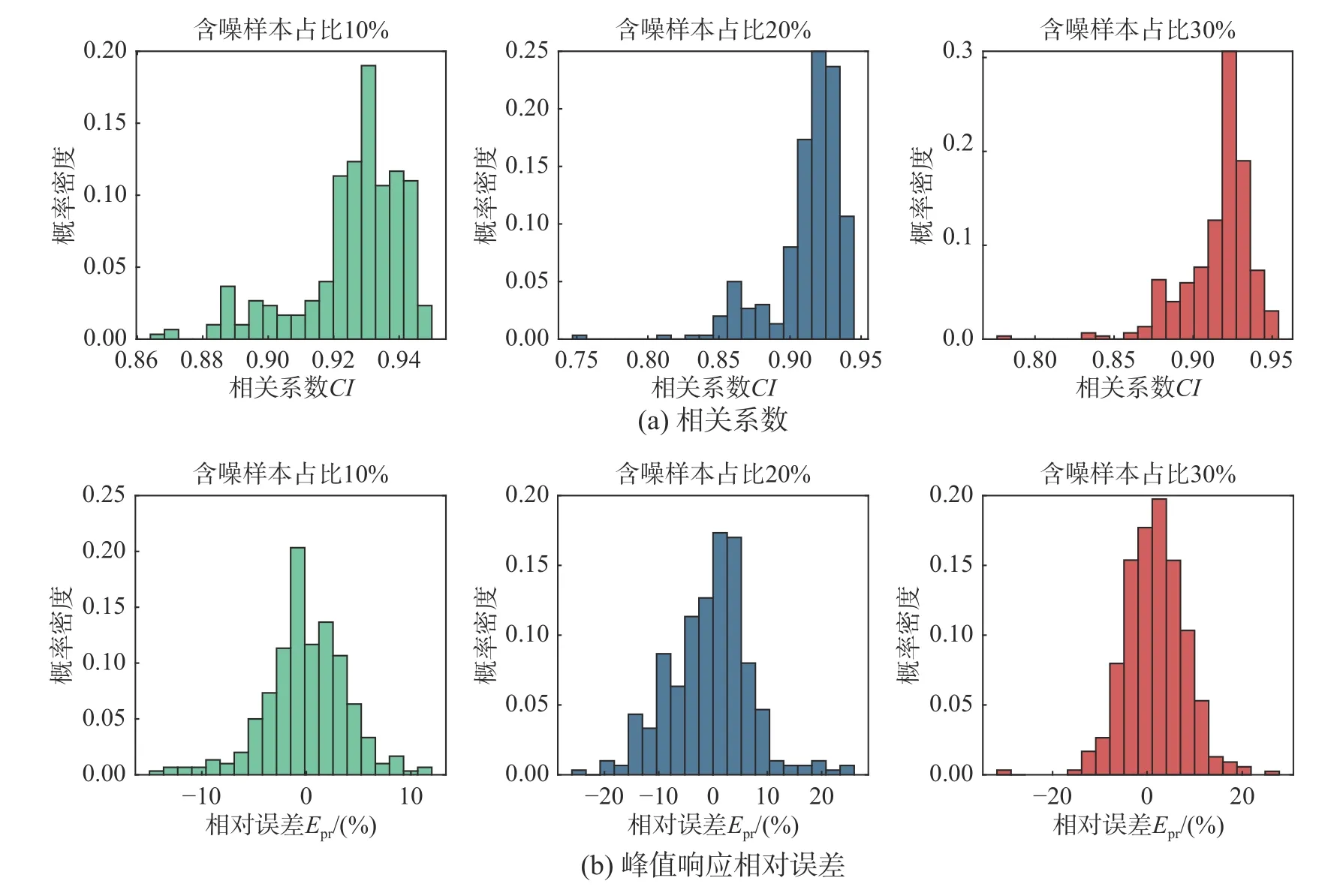
图11 不同含噪声训练样本比例下ResLSTM 网络的评价指标分布Fig.11 Evaluation index distributions of ResLSTM network with different proportion of noisy training samples

3 实桥监测数据验证

实测数据源自CESMD 数据库[41]，该数据库包含世界多地的强震记录及结构响应。选取地震记录较为丰富的美国Meloland 跨线桥，桥梁编号为Caltrans Bridge No.58-215，记录台站编号为01136。该桥为两跨预应力混凝土连续T 梁桥，墩梁固结，跨径组成为2×31.6 m= 33.2 m，标准段主梁高1.7 m，宽10.4 m；下部结构为独柱墩，圆形断面，墩高约6.4 m(自基础顶面算起)。全桥共布置32 个观测点，包含加速度、速度及位移传感器，采样频率均为100 Hz，其中6 个测点记录地震动，测点布置如图12 所示。自1979 年起，Meloland跨线桥的地震动及结构响应记录共有10 组，可用数据共9 组。其中，训练集、验证集以及测试集的样本数量依次为5 组、2 组、2 组。模型输入选取测点2 的加速度记录，输出为测点3、5、7、9、13 的位移响应。时间序列的划分窗长为10，模型训练的初始学习率为0.001，正则项系数为1×10-8，批训练样本数为5，最大训练步数为50 000。

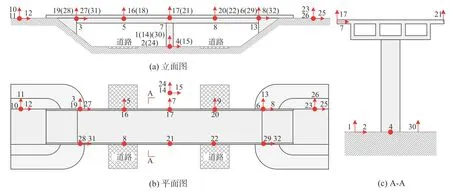
图12 Meloland 跨线桥传感器布置图Fig.12 The sensor layout of Meloland overpass

对美国1978 年Calexico 地震和2009 年Calexico地震余震的位移响应进行预测，结果如图13 所示，图上的目标值为实测的结构位移时程。因各测点的位移时程相似，此处仅列出测点7 的预测结果。可以看出，两类模型预测的地震响应在相位上与实测值吻合良好，主要差异在于响应幅值。对于Calexico 地震，两类模型预测结果较为相似，均在地震开始阶段与实测值存在较大差异，表现出与实测位移不同的振动规律；随后，两者预测值的相位与观测值趋于一致，但幅值仍有较小差异。对于Calexico 地震余震，ResLSTM 模型的预测结果与实测结果基本相同，但LSTM 模型的预测结果与实测响应明显不同，峰值响应的幅值、出现时刻均与实测响应存在显著偏差。

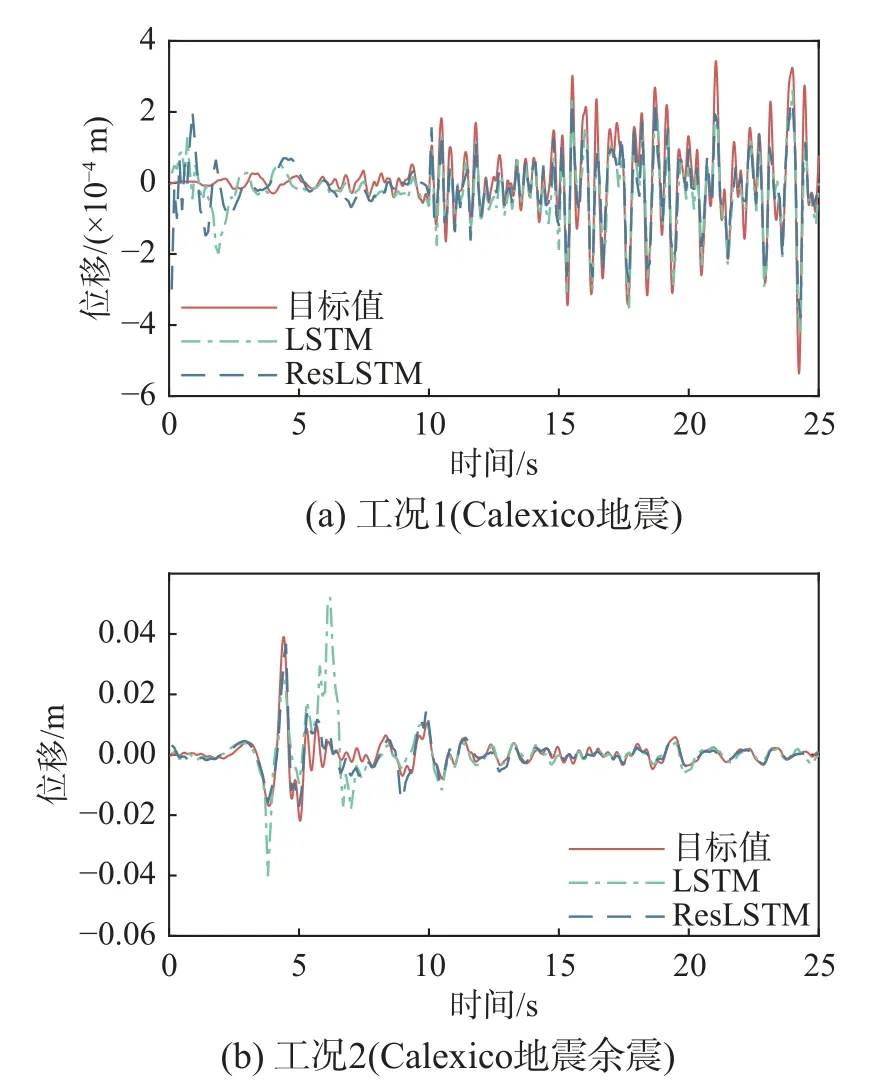
图13 Meloland 跨线桥位移响应预测对比(测点7)Fig.13 Comparison of predicted displacements of Meloland overpass (measurement node 7)

进一步地，计算预测结果与目标值的相关系数，ResLSTM 模型相关系数分别为0.2549(Calexico 地震)和0.7045 (Calexico 地震余震)。相比而言，LSTM 模型预测结果的相关系数分别为0.2313 和0.4489，预测精度远低于所提出的ResLSTM 模型。Calexico 地震响应预测精度较低的原因在于，实测响应的幅值仅为1×10-4量级，轻微的预测误差将导致预测结果的相关系数显著下降。同时，地震加速度与位移响应的测量设备不同，误差分布规律可能存在差异，导致中小地震下响应预测易出现显著偏差，而两类模型的预测结果在初始阶段(0 s～5 s)具有一定相似性，在一定程度上可以证明上述猜想。相反，Calexico地震余震的响应幅值较大，两类模型的预测精度相对良好，其中ResLSTM 模型的相关系数更达到0.7。此外，实测数据包含各类噪声干扰，也导致结构响应的预测效果表现欠佳。但是，考虑训练样本极少，地震响应的相位、峰值基本一致，说明ResLSTM 可利用少量样本预测中小震作用下的结构位移响应，并比传统LSTM 模型表现出更好的预测效果。

4 结论

本研究提出了一种层叠式残差长短时记忆神经网络(ResLSTM)，并首次应用于桥梁非线性地震响应预测。该神经网络包含2 层LSTM 层与2 层全连接层，并采用残差连接结构提升深度网络的训练效果，改善有限样本数量下的模型预测精度。通过预应力混凝土连续梁桥与组合梁斜拉桥的数值仿真算例验证，验证了ResLSTM 神经网络的预测精度与鲁棒性。同时，该方法成功应用于美国加州Meloland 跨线桥地震响应预测，并与现场监测数据对比，验证了该方法在实际工程中的预测性能。此外，采用相关研究的LSTM 神经网络作为基准模型进行对照研究，分析ResLSTM 神经网络的性能提升效果。主要结论如下：

(1) 预应力混凝土连续梁桥的数值算例表明，ResLSTM 网络的计算效率优于经典有限元方法，并表现出优良、稳定的预测效果。同时，ResLSTM网络采用了残差连接结构，使得误差能够有效地沿深度网络反向传递，最大程度保证了模型参数的优化效果，比传统LSTM 网络具有更好的预测精度和鲁棒性。

(2) 组合梁斜拉桥的数值算例表明，ResLSTM网络能够准确预测出大跨度斜拉桥的复杂非线性地震响应，预测结果的峰值、相位变化均与目标值吻合良好，并比LSTM 网络表现出更为良好和稳定的预测精度。

(3) 美国Meloland 跨线桥的现场监测试验表明，ResLSTM 网络成功利用少量观测数据预测出实际桥梁在中小地震作用下的结构响应，预测结果的相位变化与实测值吻合良好，仅峰值响应存在较小差异。此外，对于实际结构的地震响应预测，ResLSTM 网络的预测精度仍优于传统LSTM 网络。