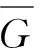群作用下逆极限空间的G-平均跟踪性和G-链传递
冀占江, 陈占和, 刘海林
(1.梧州学院 广西机器视觉与智能控制重点实验室, 广西 梧州 543002;2.梧州学院 科学研究院应用数学研究团队, 广西 梧州 543002;3.广西大学 数学与信息科学学院, 广西 南宁 530004;4.江西理工大学 理学院, 江西 赣州 341000)
0 引言
跟踪性和链传递在动力系统中占有重要的地位,是众多专家研究的热点,其研究成果见文献[1-13]。例如:文献[1]研究了平均跟踪性和q-平均跟踪性之间的关系。文献[2]在迭代系统中给出遍历跟踪性的概念并证明了一些相关的定理。文献[3]证明了fk具有平均跟踪性暗含f具有平均跟踪性。文献[4]证明了f是G-链传递与fk是G-链传递是等价的。
本文中引入G-平均跟踪性和G-链传递的概念,通过原空间和逆极限空间互相揭示的关系,在群作用下逆极限空间中研究了G-平均跟踪性和G-链传递的动力性质。
1 G-平均跟踪性
平均跟踪性的概念、度量G-空间和等价映射的概念、群作用下逆极限空间的定义、利普希茨映射的概念分别见文献[3,14-16]。
备注:根据平均跟踪性的概念,下面引入G-平均跟踪性的定义。
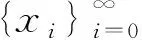
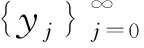
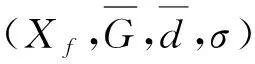
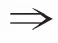
(1)
其中M=diam(X)。
取
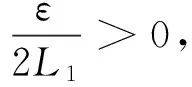
(2)
由于f的利普希茨常数为L,因此∀x,y∈X,∀i≥1,有
d(fi(x),fi(y))≤Lid(x,y)。
(3)
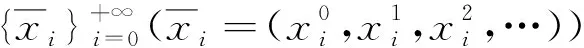
故
则

(4)
令
由于f是满射,可取
因此
由式(1)、(3)知
则
由式(4)知,
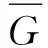
对δ2>0,则存在m′>0使
(5)
由于C为f-1的利普希茨常数,因此∀x,y∈X,∀i≥1,有
d(f-i(x),f-i(y))≤Cid(x,y)。
(6)
令
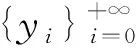
(7)
令
根据f是满射的,可取
由式(5)—(7)知,对任意的k≥0,有
因此,
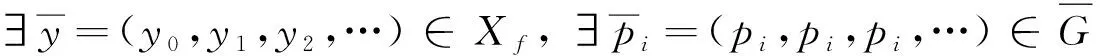
因此
故f具有G-平均跟踪性。
2 G-链传递
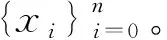
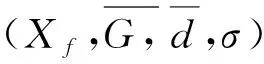
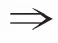
(8)
其中M=diam(X)。
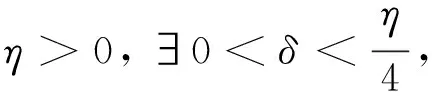
(9)

由f等价和式(9)知,∀0≤j≤m,∀0≤i≤n,有
(10)
令
由于f是满射,因此可取
取
由式(8)、(10)知,


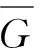
因此
即

3 总结