两桥臂交叉解耦不平衡控制策略研究

谢锡锋, 孔繁镍, 舒泽亮, 左江林, 张帅

(1.广西水利电力职业技术学院 电力工程学院, 广西 南宁 530023;2.广西大学 电气工程学院, 广西 南宁 530004;3.西南交通大学 电气工程学院, 四川 成都 6117561)

0 引言

由于低压配电网用户单相负荷的随机接入,导致三相电网有功电流不平衡和无功增加[1],因此治理该电能质量问题成为三相电网亟待解决的关键问题。静止无功补偿装置是一种改善电网电压波形和提高三相电网功率因数的灵活装置,能有效解决各种负载带来的无功冲击[2]。常用的三相无功补偿装置一般由三桥臂组成[3]。这种三相拓扑在控制策略实现时,各相之间不存在耦合,被广泛应用在三相系统中[4-5],然而三桥臂中较多的开关管、传感器等增加了系统的体积和硬件成本。

为了降低成本,基于LC滤波器的混合补偿拓扑被提出。该方案控制系统中包含上、下变换器控制单元以及共用控制模块,但是这种拓扑需要依靠外部硬件实现三相电网单位功率因数运行[6-7]。为了减少桥臂数量,基于两桥臂的三相有源电力滤波器(active pouer filter, APF)方案被提出,第三相与直流电容的正端或负端相连,这种拓扑可以补偿负载的无功和谐波,但也会产生较大的直流偏置电压[8-10]。为了克服这一缺点,文献[11-14]中提出了四开关三相变换器,该拓扑通过分电容构建三相APF的第三桥臂,然而该变换器在传统控制策略上无法有效抑制不平衡有功。为了减少开关管个数,文献[15-16]中采用了基于交流耦合电感和LC滤波器的两桥臂变换器,但其无功补偿能力有待提高。为了提高电压补偿与无功补偿能力,文献[17]中设计一种新型变换器,其比传统无功补偿装置多了一个开关和一个耦合电容,但系统之间存在耦合。为了消除系统之间的耦合,文献[18]中采用模型反演理论对所建静止无功发生器(static var generator, SVG)解耦模型进行控制,实现桥臂电流保持稳定,但由于采用非线性控制方法,控制器参数整定复杂。为了提高三相电流质量,文献[19]中提出一种不平衡负载下SVG分序控制策略,采用重复控制和比例积分控制相结合的方法补偿零序电流,但其未考虑SVG接入点的过电压对功率潮流的影响。为了提高系统的功率因数,文献[20]中利用单相分布式发电智能逆变器对三相配电系统中的负序和零序电流进行补偿,但其运算复杂。为了消除三相电流不平衡,文献[21]中使用分布式静态串联补偿器向电网注入无功电压来补偿无功功率,但其在不平衡电压下难以精确地锁定电压相位,导致系统动态性能不足。为了精确锁定电网电压不平衡下的电压相位,文献[22]中提出了一种改进型的锁相环(phase-Locked loop, PLL)设计方法。

为了减少开关管和无源器件个数并提升三相电网电能质量,本文在两桥臂变换器的基础上利用两相负载的特性提出一种两桥臂交叉解耦不平衡控制策略,利用多变量滤波器(multiple variable filter, MVF)和交叉解耦双复系数滤波器(double complex coefficient filter, DCCF)优化PLL,解决了传统PLL在谐波严重畸变和电网电压不平衡下难以精确锁定电压相位和频率的问题,所提控制策略可以利用两桥臂变换器补偿三相电网有功、无功,抑制三相有功不平衡及无功对三相电网的影响,将三相电网功率因数从0.257提升至0.997,三相电流的不平衡度从150.0%降低至2.6%,显著减少了三相无功补偿器的开关管个数。

1 两桥臂变换器工作原理

1.1 拓扑及功率流动分析

三电平两桥臂变换器的拓扑结构如图1所示。图中Vsa、Vsb和Vsc为三相电网电压,isa、isb和isc为三相电网电流。两桥臂变换器主要由A相桥臂、B相桥臂,滤波电感La、Lb以及直流电容Cdc1、Cdc2组成。该拓扑中单相桥臂A和B分别与三相电网的Vsa和Vsb相连,变换器分电容的中点与Vsc相连。ica、icb分别为A相、B相桥臂输出电流,icc为通过电容中点流入C相的电流,iLa、iLb和iLc为负载电流。对于三相三线电网,当A相和B相电网电流为平衡的有功电流时,根据基尔霍夫电流定律可知,三相输入电流平衡且具有单位功率因数,此时只需根据两相负载的无功电流进行补偿,即可保证三相电网电流平衡且具有单位功率因数。

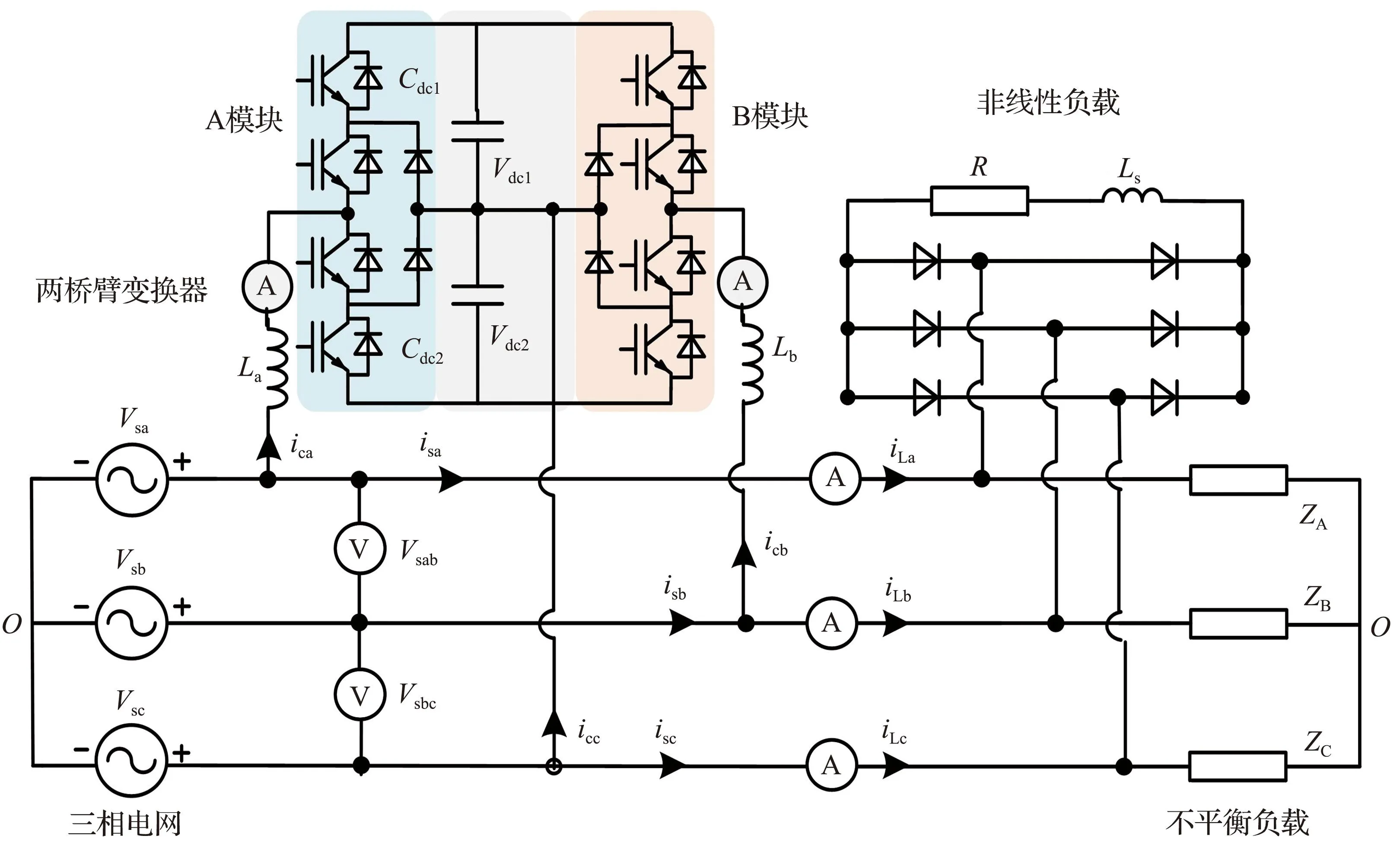
图1 三电平两桥臂变换器的拓扑结构Fig.1 Topology of the three-level two-leg converter

1.2 非不平衡控制策略

非不平衡控制策略中A相和B相变换器分别根据各自负载的无功进行补偿,此时变换器的无功补偿电流幅值为负载无功电流幅值,即补偿无功电流和负载无功电流满足icaq=-ilaq,icbq=-ilbq,icaq与icbq分别为A相和B相的补偿无功电流,ilaq与ilbq分别为A相和B相的负载无功电流。

根据非不平衡控制策略中补偿电流的计算公式、三相电压电流和A、B相变换器的相位关系可以得到负载所需的有功电流。

(1)

式中:icadref和icbdref分别为A相和B相有功电流参考值;icaqref和icbqref分别为A相和B相无功电流参考值;iLaq和iLbq分别为A相和B相负载的无功电流;iLad、iLbd和iLcd分别为A相、B相和C相负载的有功电流。

不同控制策略的电压电流矢量关系如图2所示。由图2(a)可以看出,非不平衡控制策略无法完全补偿负载的无功和平衡三相电网的有功。由图2(b)可知,即使负载为无功和不平衡有功,经过所提两桥臂交叉解耦不平衡控制后,三相电网电流保持平衡且具有单位功率因数。

(a) 非不平衡控制策略 (b) 两桥臂交叉解耦不平衡控制策略图2 不同控制策略的电压电流矢量关系Fig.2 Vector of voltage and current with different control strategies

2 两桥臂交叉解耦不平衡控制策略

2.1 负载有功无功电流检测

在平衡负载有功、补偿无功时,需要根据负载有功电流和无功电流分别注入一定数值的有功电流和无功电流,才能使得三相电网电流平衡且具有单位功率因数。以变换器A相为例,A相电网电压、补偿电流和负载电流分别为

(2)

式中:ω为电网电压角速度;ωta为A相网侧电压的相位。负载电流包含谐波、无功电流和有功电流,根据各自的相位检测出负载的无功电流,表示为

(3)

式中iha为谐波电流。将式(3)中的计算结果经过10 Hz低通滤波器后,再与2相乘,即得到负载的无功电流幅值。负载有功电流的检测方法与无功电流类似。系统有功参考电流均值可以表示为id*=(iLad+iLbd+iLcd)/3。

2.2 两桥臂交叉解耦不平衡控制策略

三相电网的相电压和2个背靠背变换输入电压相角差满足φac=φa-30°,φbc=φb+30°。根据有功电流、相角差和负载无功可得,两桥臂交叉解耦控制策略下有功补偿电流为

(4)

由式(1)、(4)可得,A、B两相的有功补偿电流为

(5)

同理,A、B两相的无功补偿电流为

(6)

由式(1)、(6)可得,A、B两相补偿无功电流的参考值为

(7)

令iLbq=0,由式(5)、(7)可得,线电压相位参考下的补偿电流的有功无功参考值为

(8)

两桥臂交叉解耦不平衡控制框图如图3所示,其主要由有功无功检测以及交叉解耦控制2个部分组成,φa、φb、φc分别为A相、B相和C相网侧电压初相位,vdc*与vdc分别为直流电压给定值与实际直流电压值,icd*与icad分别为有功电流给定参考值与实际有功电流,icq*与icaq分别为无功电流给定参考值与实际无功电流,Vsm为网侧电压有功分量。

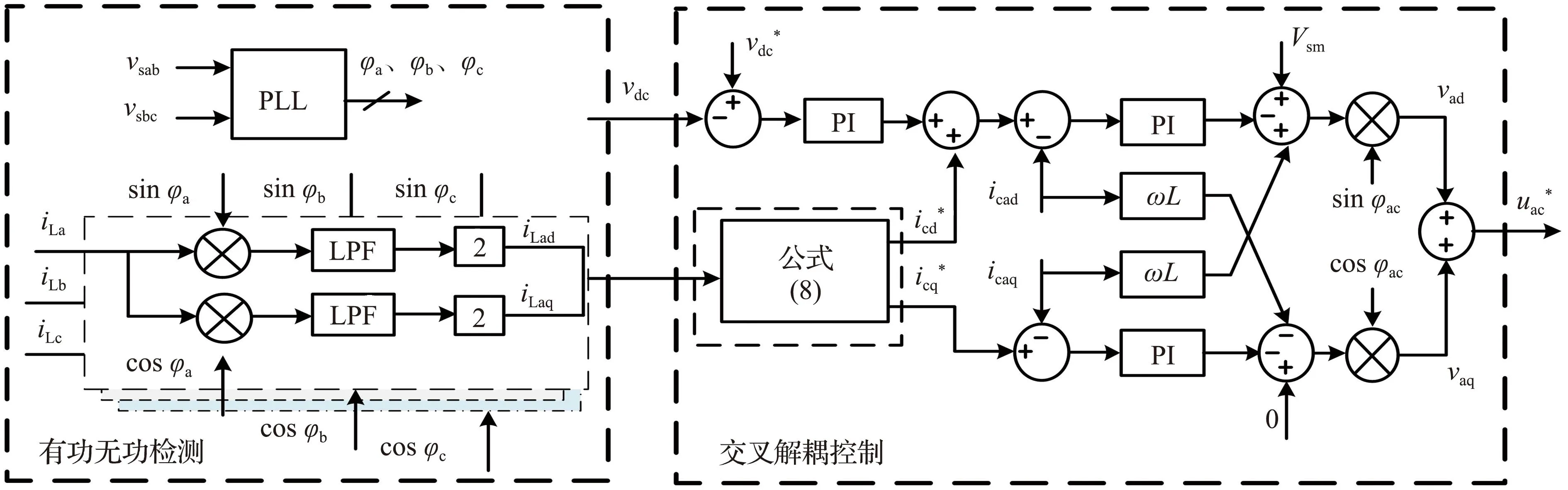
图3 两桥臂交叉解耦不平衡控制框图Fig.3 Proposed cross decoupling unbalance control strategy based on two-leg converter

采用DCCF分离和提取电压正、负序分量,解耦了不平衡电网下正、负序分量。利用MVF对输入电压基波正序分量幅值无衰减、零相移特性,将MVF引入DCCF中,滤除输入DCCF结构的谐波,将PLL输出角频率反馈回DCCF,解决了传统PLL在电网谐波畸变和电压不平衡下难以精确锁相的问题。改进的新型PLL结构如图4所示。

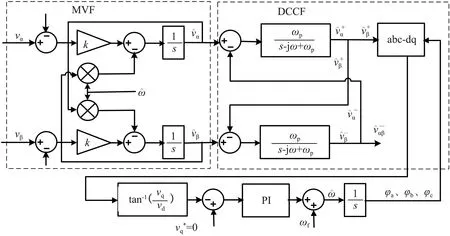
图4 新型PLL结构Fig.4 Structureof a new PLL

MVF中输入输出方程为

(9)

DCCF中输入输出方程为

(10)

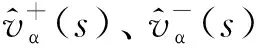
3 仿真与实验验证

3.1 仿真验证

三电平两桥臂变换器平台的仿真参数见表1。为了验证所提两桥臂交叉解耦控制策略对于三相不平衡负载电流的补偿效果,根据图1和表1,利用MATLAB/Simulink搭建平台,进行仿真验证。

表1 仿真参数Tab.1 Parameters of the simulation

三相电网不仅存在平衡负载,也存在有功、无功不平衡负载,而不平衡的极端条件为三相负载缺相。B相负载缺相时,三相有功不平衡和无功补偿动态实验结果如图5所示,其中,PFa、PFb、PFc分别为a、b、c三相的功率因数。图5(a)中,在仿真时间为2 s时,BC之间断开,AC之间的负载由6 Ω、15 mH突变为3 Ω、7.5 mH,约经过0.06 s,系统达到新的平衡,补偿前,三相负载电流有效值分别由135.40、0、135.40 A变为80.47、0、80.47 A,最小功率因数仅有0.497,不平衡度为150%,而补偿后,三相电网电流有效值分别由64.65、64.27、64.35 A变为41.48、41.25、41.17 A,不平衡度仅为0.75%,功率因数达到0.999。

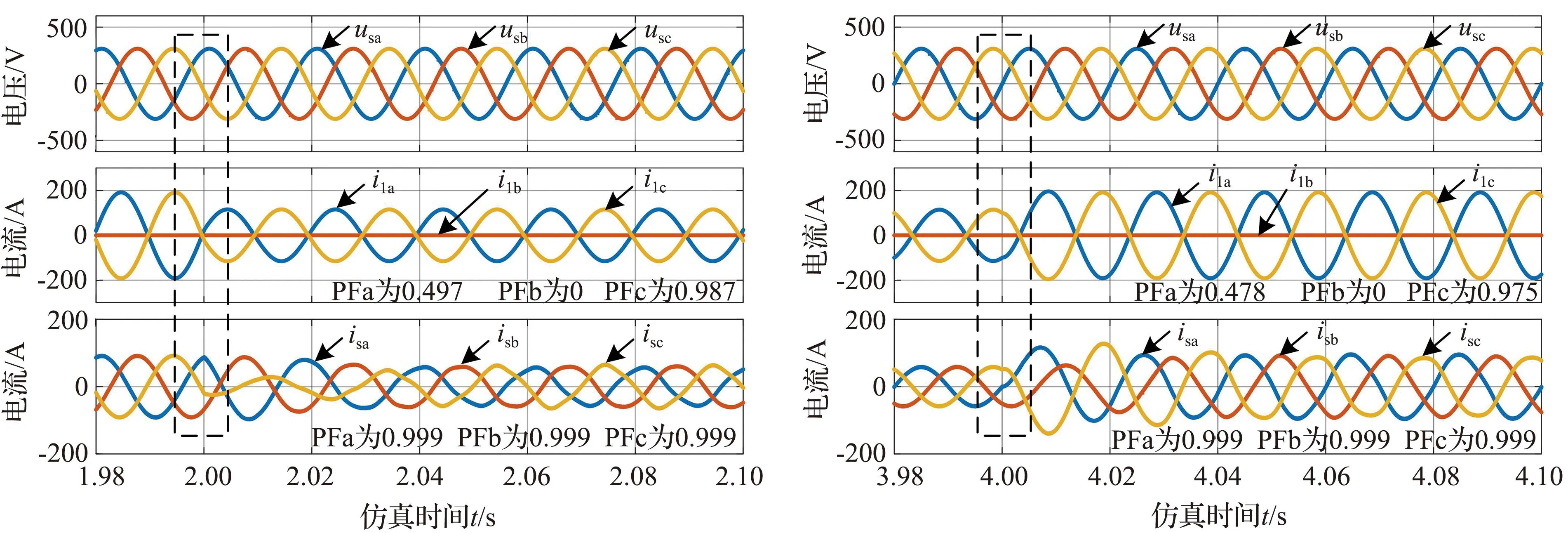
(a) 负载增大实验 (b) 负载减小实验图5 有功不平衡和无功补偿动态实验结果Fig.5 Unbalance active and reactive compensation results

图5(b)中,在仿真时间为4 s时,BC之间断开,AC之间的负载由3 Ω、7.5 mH突变为6 Ω、15 mH,约经过0.06 s,系统达到新的平衡,三相负载电流有效值分别由80.47、0、80.47 A变为135.40、0、135.40 A,最小功率因数仅有0.478,不平衡度为150.0%,三相电网电流有效值分别为41.48、41.25、41.17 A变为64.65、64.27、64.35 A,不平衡度仅为0.58%,功率因数达到0.999。

仿真结果表明,所提出的控制策略能够快速、有效平衡三相不平衡有功电流和补偿三相无功电流,确保三相电网电流为正弦波,且单位功率因数运行。

3.2 实验验证

实验参数见表2。根据图1和表2,搭建了三电平两桥臂变换器,实验平台如图6所示,主要由主电路板、采样板和电源板组成。

表2 实验参数Tab.2 Parameters of the experiment

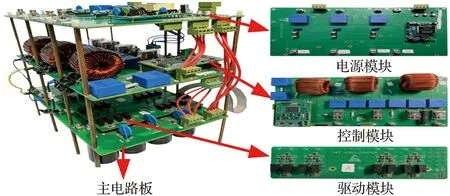
图6 实验平台Fig.6 Prototype photograph of two-leg converter

变换器启动与补偿稳定实验结果如图7所示。系统首先进入初始状态,当状态机检测到输入电压正常、锁相完成后通过三相不控整流桥电路对直流电容进行充电,充电完成且直流电压稳定后开始进入工作状态,具体实验结果如图7 (a)所示。在启动过程中,变换器不存在直流电压跌落和超调,输入电流冲击小,分电容电压始终保持均衡,因此所提控制策略可以保证两桥臂变换器安全可靠启动。变换器补偿稳定后端口电压与直流电容电压波形如图7 (b)所示,2个变换器的端口电压相差120°,脉动的功率造成的直流电容电压波动幅值在允许范围内,可以看出所设计的参数符合实验要求。

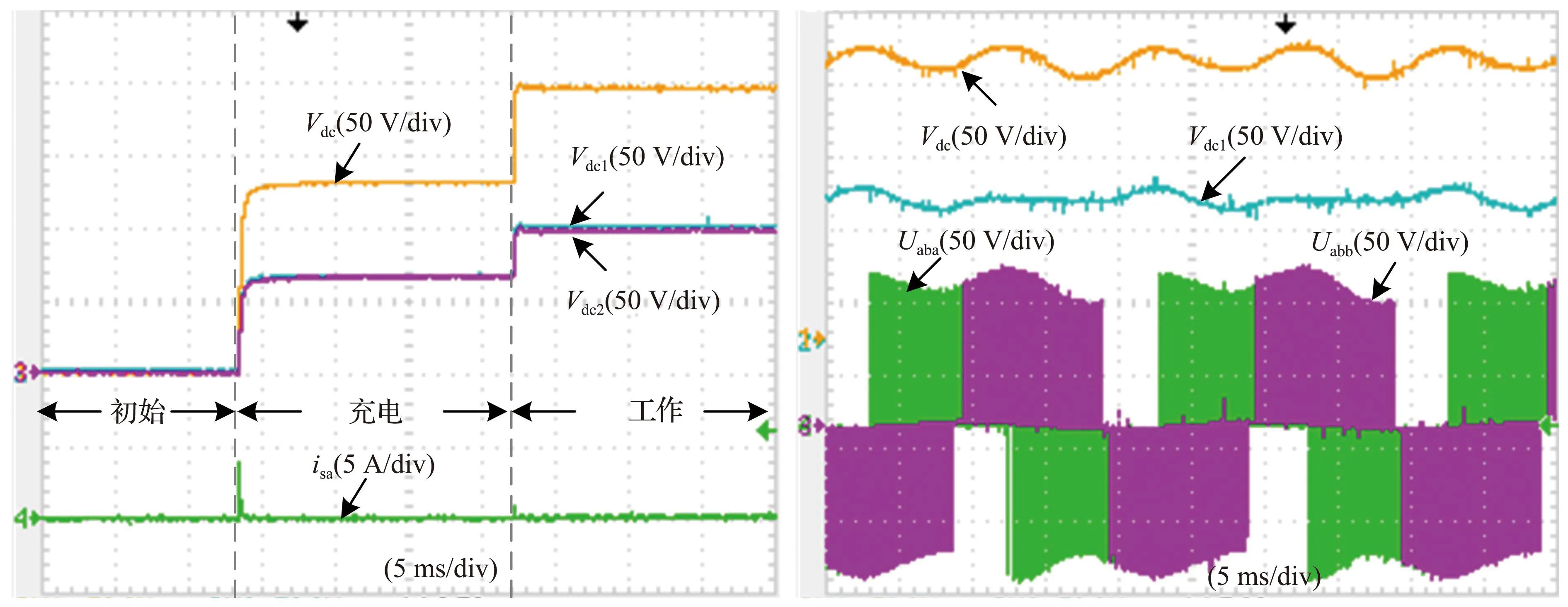
(a) 启动直流电容电压 (b) 补偿稳定后端口电压图7 启动与补偿稳定实验结果Fig.7 Experiment results of startup and compensation

负载为平衡无功时所提控制策略补偿实验结果如图8所示。当三相负载为平衡无功时,各控制策略的对比,其中THDa、THDb、THDc分别为a、b、c三相的总谐波失真率,PFa、PFb、PFc分别为a、b、c三相的功率因数。由图8(a)可知,三相电网的功率因数分别为0.459、0.445和0.413,严重影响了三相电网电能质量。采用所提两桥臂交叉解耦不平衡控制后,三相电流及功率因数如图8(b)所示,三相电网的功率因数分别提升至0.999、0.998和0.994,且三相有功电流平衡,因此所提控制策略能够显著降低负载无功对三相电网的影响。

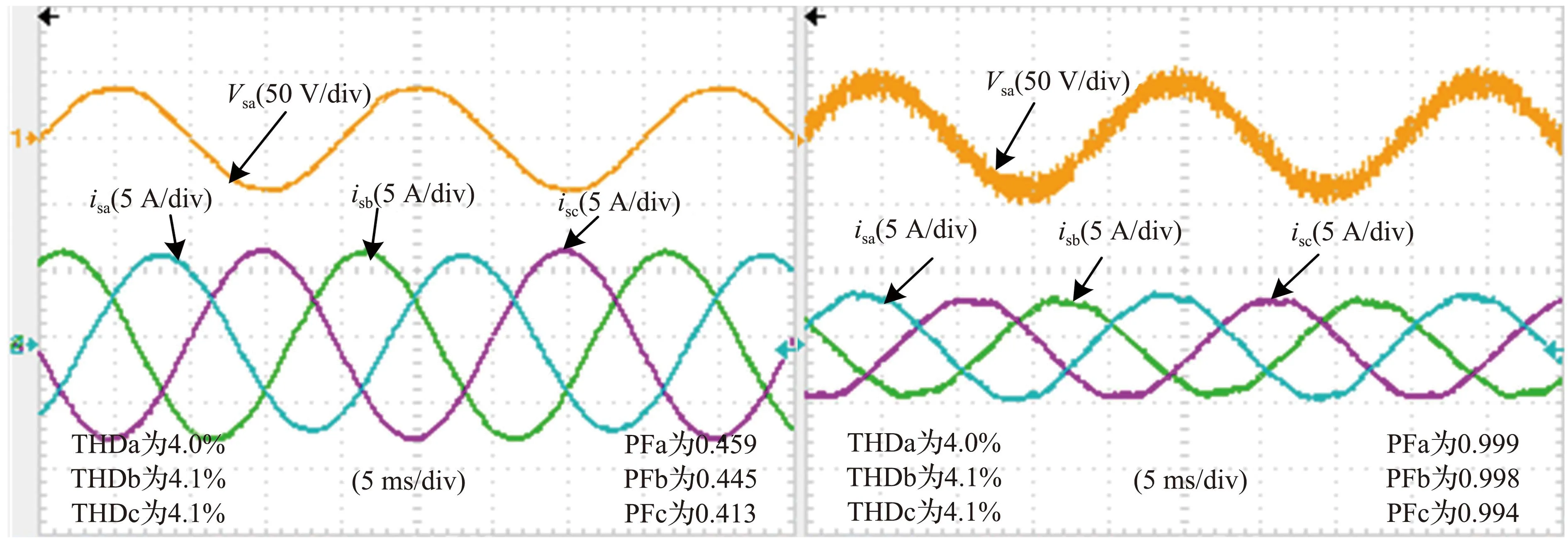
(a) 补偿前三相电流及功率因数 (b) 补偿后三相电流及功率因数图8 负载为平衡无功时所提控制策略补偿实验结果Fig.8 Experiment results of proposed control strategy with balanced reactive load

负载为不平衡无功时所提控制策略补偿实验结果如图9所示。由图9(a)可知,三相电流的有效值分别为5.88、0、5.88 A,三相电流的不平衡度为150.0%,且两相负载的功率因数分别为0.257、0.988,表明负载缺相后三相电网电能质量受到了严重影响。采用所提交叉解耦不平衡控制后,由图9(b)可知,三相电流的有效值分别为3.07、3.06、2.99 A,三相电流的不平衡度降低至2.6%,电网三相功率因数分别提升至0.997、0.999、0.997。

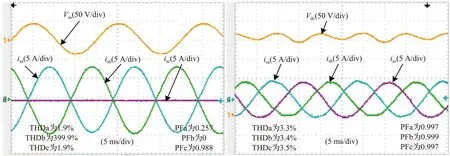
(a) 补偿前三相电流及功率因数 (b) 补偿后三相电流及功率因数图9 负载为不平衡无功时所提控制策略补偿实验结果Fig.9 Experiment results of proposed control strategy with unbalanced reactive load

根据图8、9所示的实验结果可以看出,所提交叉解耦不平衡控制策略结合两相半桥背靠背变换器在负载为平衡无功和不平衡无功时,均可以保证三相电网电流平衡且具有单位功率因数。

所提的电路拓扑和控制方法与文献[23-26]进行对比,不同电路拓扑和控制方法的比较分析见表3。由表3可知,所提出的拓扑结构开关管数量最少,在交叉解耦不平衡控制策略下,三相电流不平衡度和THD最小,功率因数最大。

表3 不同电路拓扑和控制方法的比较分析Tab.3 Comparative analysis of different circuit topologies and control methods

4 结论

针对非不平衡控制策略中没有考虑线电压和相电流的相角差,造成三相电网的有功、无功电流无法完全补偿的问题,提出一种两桥臂交叉解耦不平衡控制策略,得到结论如下:

① 提出一种两桥臂交叉解耦不平衡控制策略,分别对2个单相背靠背变换器的无功电流进行控制,利用两桥臂变换器补偿三相不平衡无功。

② 利用MVF和DCCF优化PLL,解决了传统PLL在电网谐波畸变和电压不平衡下难以锁相的问题。

③ 所提控制策略能利用两桥臂变换器抑制三相有功、补偿三相无功,三相电流的不平衡度从150.0%降低至2.6%,三相电网功率因数从0.257提升至0.997。