基于优化奇偶重构法的光伏阵列自适应重构技术设计

易灵芝,程斯岳,王雅慧,2,罗伯特,范 律,谭靖萱

(1. 湘潭大学 自动化与电子工程学院&湖南省多能源协同控制技术工程研究中心,湖南 湘潭 411105;2. 湖南大学 电气与信息学院,湖南 长沙 410082;3. 威胜信息技术股份有限公司,湖南 长沙 410205)

0 引言

随着光伏发电成本的逐步下降,光伏系统的应用场景越来越广泛,光伏发电在电力系统中扮演的角色也越来越重要,太阳能是最丰富的能源来源之一,并且可以长期使用[1]。此外,近年来光伏发电技术的重要性令人震惊[2]。但是,现实生活中存在有各种因素导致光伏阵列的输出功率降低,其中一个主要因素是局部阴影[3]。局部阴影是由云,建筑物,树木等造成的,局部阴影的产生会使得光伏阵列所产生的最大功率降低[4,5],而影响系统的整体性能,从而导致严重的功率损耗。针对此类情况,主要利用光伏重构技术来降低对系统发电的影响,光伏重构技术主要分为动态重构技术以及静态重构技术。动态重构的基本原理是在光伏阵列中引入一个电力电子开关,利用专门的控制器发送信号控制开关的通断,从而动态改变光伏电池的排列顺序,实现阴影分散;静态重构技术是指在不改变系统连接方式的情况下,通过预先分散位置对光伏阵列进行静态的物理重构。通过这种方式,以较低的成本大大降低了典型局部阴影下光伏阵列行电流的不平衡。通过平衡行电流来削减甚至消除多峰,这直观地增加了光伏输出功率,并间接降低了对全局最大功率追踪(Global maximum power point tracking, GMPPT)的精度要求[6]。常见的动态重构技术有粒子群优化(Particle Swarm Optimization, PSO)[7], 改进哈里斯鹰优化器(Modified harris hawks optimizer, MHHO)[8], 多目标灰狼优化器(Multi-Objective Grey Wolf Optimizer, MOGWO)[9], 蜜獾算法(Honey badger algorithm, HBA)[10],两步遗传法(Two step GA)[11]等。常见的静态重构技术有数独法(So Du Ku)[12,13],洛书法(Lo Shu)[14],幻方法(Magic Square, MS)[15],奇偶重构法(Odd Even Configuration, OEC)[16]等。其中,OEC奇偶重构法将光伏阵列的行和列分为了奇偶两组,然后按照既定的规则对其进行重新组合,该方法构造简单,适合于各种尺寸的光伏阵列,但是针对一些特殊形状的阴影分布可能达不到良好的分散效果[17]。光伏阵列常见的结构可以分为串并联(Series-Parallel, SP), 蜂巢(Honey-Comb, HC), 桥接(Bridge-link, BL), 全交叉连接(Total Cross Tied, TCT)[18],其中对于TCT结构的研究最具有实用价值,因此本文同样对TCT结构进行研究。TCT 结构阵列静态重构应遵循以下两条原则:不改变光伏组件所在列的位置;将同行光伏组件尽可能多的分散到不同行中,从而最大限度的均衡阵列每行光辐射照度,并简化模块之间的连接[19]。光伏阵列分类大致上如下图1所示[17]。

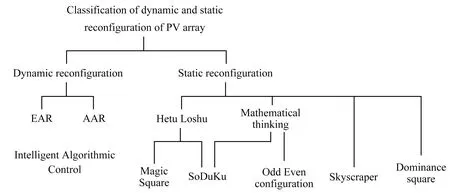
图1 光伏阵列重构方法分类

在OEC奇偶重构法的研究过程中,研究人员对其进行了多种改进,本文针对OEC奇偶重构法的一些缺点,提出一种优化的OEC奇偶重构法(Optimized Odd Even Configuration, OOEC)。该方法主要优势为

(1) 保留了传统OEC奇偶重构法的简单性能,能够对光伏阵列起到一个很好的阴影分散作用,并且有效地减少光伏发电过程中的多峰现象。

(2) 引入了自适应阵列重构 (Adaptive array reconfiguration, AAR) 技术,该技术将阵列分为了自由重构模块和固定重构模块。根据产生阴影的情况改变连接到每行固定面板上的自适应面板的数量,实现光伏阵列重构。

(3) 结合了OEC奇偶重构法和AAR技术的优势,达到有效地增加最大功率输出的效果。

本文结构如下:第1节介绍光伏阵列的特性以及常见结构;第2节介绍本文所采用的优化OEC奇偶重构法;第3节进行仿真实验验证,对光伏阵列进行重构前后的对比;第4,5节为结果与总结。

1 光伏阵列建模

光伏发电系统通常采用TCT连接,同一列的光伏组件串联连接,同一行的并联连接,该类拓扑具有最稳定的拓扑结构和最高的输出效率。

为了研究多种类型条件下遮挡或光伏阵列损坏对太阳能光伏系统的影响及其缓解措施,建立光伏阵列的数学模型。首先,进行一个单一的光伏模块的模型开发,然后多个这样的模块互连在不同的配置,从而构建一个光伏阵列[20],如图2所示。

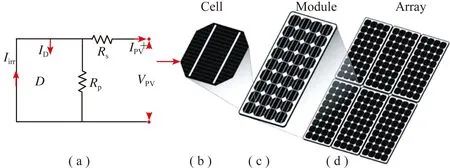
图2 光伏电池-光伏组件-光伏阵列构成过程

单个光伏电池建模如图2所示,其发电电流为

(1)

式中Iirr表示光生电流,ID表示等效二极管反向饱和电流,q表示单位电荷量,n表示二极管特性因子,k表示玻尔兹曼常数,T表示温度,Rp表示等效并联电阻, 近似为无穷大,Rs表示等效串联电阻,非常小可忽略不计,VPV、IPV分别为光伏组件的输出电压和输出电流[21,23]。

基于光伏阵列模型,搭建6×6光伏阵列实现小功率光伏发电系统(见图3),其输出电压Vout和输出电流Iout分别为

(2)

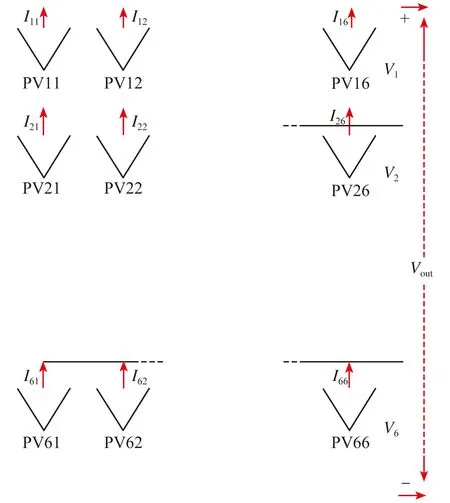
图3 由6×6TCT光伏阵列实现光伏发电系统

式中i=1,2……M,j=1,2……N,M和N分别为光伏屋顶中光伏阵列的行数和列数的值,Vmax i为光伏阵列的第i行的最大输出电压,Iij为光伏阵列的第i行第j列的光伏阵列输出电流[24,25]。

2 OOEC方法说明

Karan Y等人在2020提出OEC奇偶重构法,经典的OEC奇偶重构法操作简单快捷,将TCT光伏阵列分为奇数行和偶数行,能够在一定程度上减少光伏阵列发电过程中的多峰现象,保证光伏发电系统的稳定性,其数学表达式如下所示。

对于一个m×n的光伏阵列,其电气连接在第i行和第j行的模块的行指数(物理位置)由以下方法确定。对于连接在任意一列第一行的模块,其行指数可表示为[26]

R1j=1+(j-1)2,

(3)

对于奇数行电气连接的所有其他模块

(4)

对于偶数行电气连接的所有其他模块

(5)

根据数学表达式可以得出OEC奇偶重构法下的光伏阵列连接,由于光伏阵列第一列在本文所提出的优化OEC奇偶重构法中作为了自由重构模块,因此下图4直接从第二列开始进行说明[26]。

图4 OEC奇偶重构法下光伏阵列互联

由于传统的OEC奇偶重构法的循环上限会导致部分列的排列相同,为了尽可能在小阵列中分散光伏阵列的行组件,导致循环过快;当局部阴影超过4列时,阵列优化的效果较差。因此本文将对OEC奇偶重构法(OOEC)进行优化,OOEC奇偶重构方法步骤如下:

第一步:将原TCT阵列分为两部分:自由重构部分和固定重构部分。第一列的光伏阵列为自由重构部分,其可以自由确定位置,以此来确保最小的行电流约束。因此6×6光伏阵列分为了第一列的自由重构模块以及一个6×5光伏阵列,如图5所示。

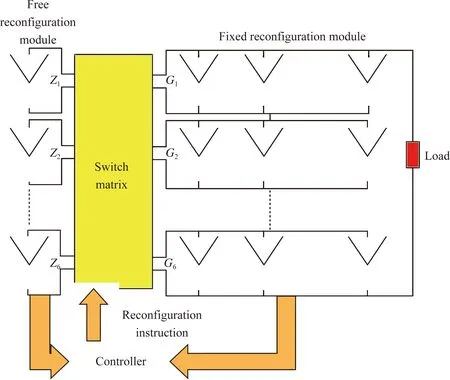
图5 光伏阵列总体结构重构说明

第二步:光伏阵列中每一列分为奇数行组件和偶数行组件,例如在图7(a)中,每一列的组件都被分为奇数行组件1、3、5和偶数行组件2、4、6。然后将奇数列的奇数行组件在上、偶数行组件在下,按顺序连接在一起,偶数列的偶数行组件在上、奇数行组件在下,按顺序连接在一起。在图7(b)中,第1列(原6×6光伏阵列第2列)的行排列为1、3、5、2、4、6,第2列的行排列为2、4、6、1、3、5,第3列的行排列为1、3、5、2、4、6,第4列的行排列为2、4、6、1、3、5,然后以此类推,完成重构第一步。

第三步:将执行完第一步得到阵列的第2列(原6×6光伏阵列第3列)向上循环1行得到最终优化阵列新的第2列,第3列为向上循环2行,第4列为向上循环3行,以此类推,便得到了最终重构后的光伏阵列组件位置。例如在图6(c)中,第2列最终行排列为组件4、6、1、3、5、2,第3列的行排列为5、2、4、6、1、3,第4列的行排列为1、3、5、2、4、6,第5列的行排列为4、6、1、3、5、2。

图6 OOEC方法重构步骤图

自由重构模块不进入常规的OEC奇偶重构法之中,将之独立而出,并且本文对其提出了一种新的开关结构用来控制自由重构模块,如图7所示。

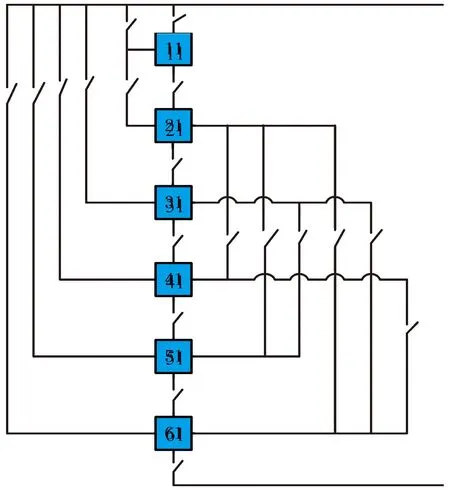
图7 自由重构模块开关布置图

如图7所示,利用此开关结构可以最大程度的将第一列的自由重构模块中所包含的每一块光伏阵列分布至每一列,继而均衡光伏阵列的行电流,控制行电流偏差最小,减少光伏多峰现象。

3 仿真实验验证

首先,对本文所进行仿真实验的不同方法以及不同情况下的功率进行说明(表1),6×6光伏阵列在1 000 W/m2的均衡光照强度下输出功率为6 576 W,如图8所示。

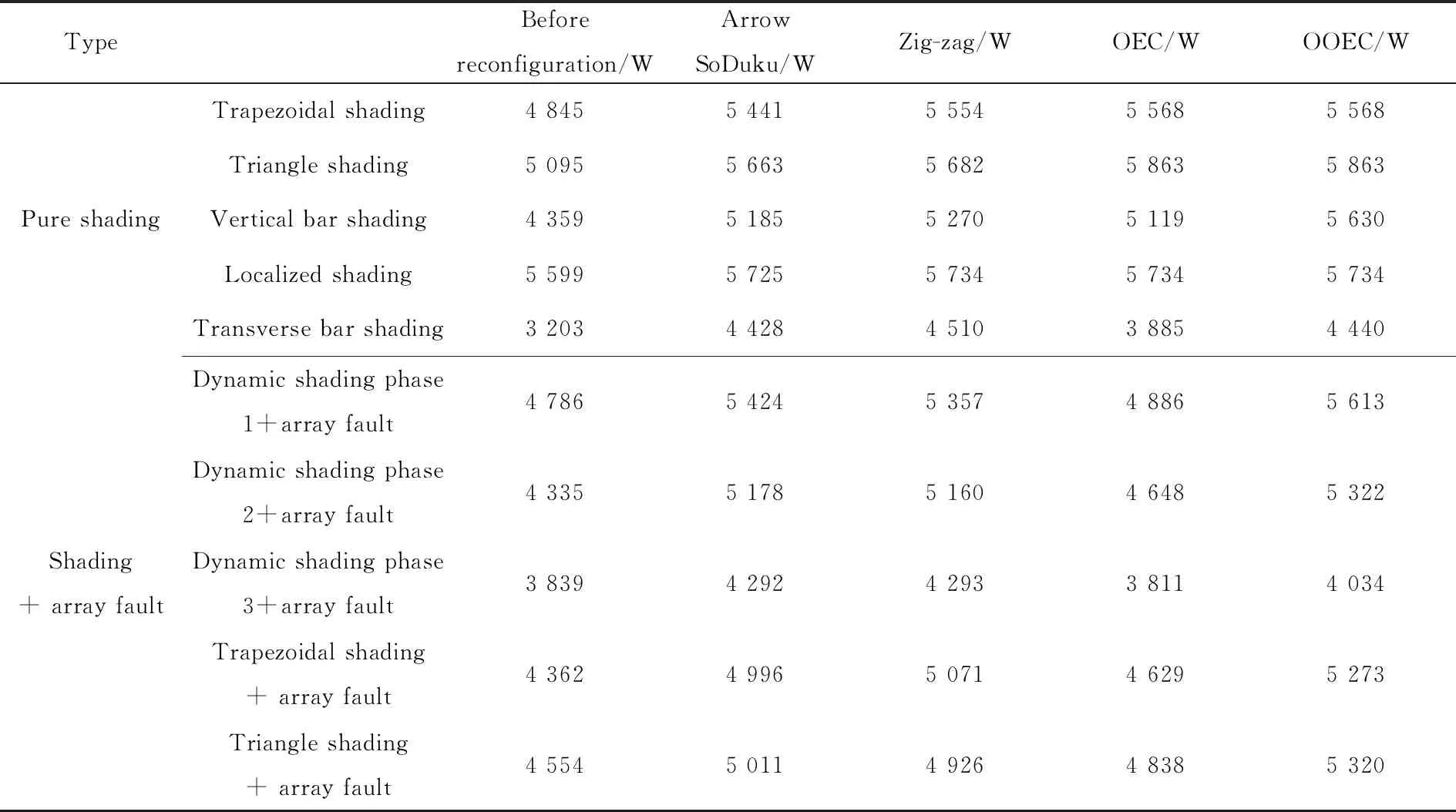
表1 功率汇总表

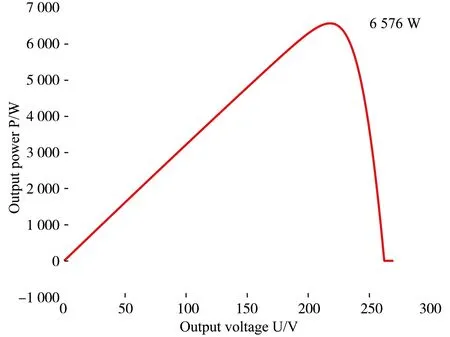
图8 无阴影遮挡时6×6光伏阵列PU输出特性曲线

对于仿真实验设置三种类型:(1) 部分阴影遮挡,(2) 动态阴影遮挡加光伏阵列损坏,(3) 普通阴影遮挡加光伏阵列损坏。其中部分阴影遮挡情况下设置五种情况,分别为:梯形阴影,三角形阴影,竖长条形阴影,局部形阴影,横长条形阴影。动态阴影遮挡加光伏阵列损坏情况分为三阶段,阴影遮挡加光伏阵列损坏分两种类型,分别为梯形阴影情况下光伏阵列损坏,三角形阴影情况下光伏阵列损坏。并将本文所提出的OOEC方法与OEC奇偶重构法[26],Arrow So Du ku[27],Zig-zag[28]进行PU输出特性曲线的对比,通过失配损耗,功率提升百分比,性能比,均衡指数[29]等评价指标(见表2),最后得出仿真实验结论。

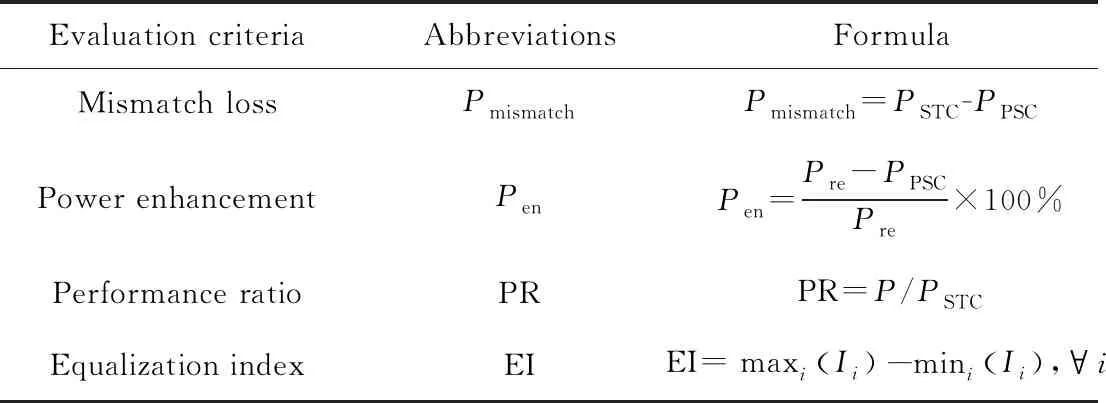
表2 评价标准概述

表2中,PSTC代表标准情况下光伏阵列输出功率,PPSC代表阴影遮挡情况下光伏阵列输出功率(包含阵列故障情况),Pre代表光伏阵列重构后的输出功率。

(1) 部分阴影遮挡情况。光伏阵列重构前,部分阴影遮挡情况如图9所示,图9(a)表示梯形阴影遮挡, 图9(b)表示三角形阴影遮挡, 图9(c)表示竖长条形阴影遮挡, 图9(d)表示局部形阴影遮挡, 图9(e)表示横条形阴影遮挡。如图9所示,在五种情况下的光伏阵列受到阴影遮挡,会导致其发电出现波动,并且出现多峰现象。因此需要对其进行光伏重构,确保其发电稳定,减少电能损失。

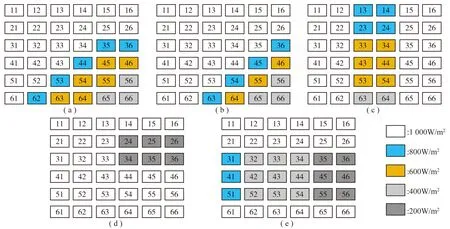
图9 光伏阵列部分阴影遮挡情况

利用Arrow So Du ku进行重构之后,可以得到如图10所示的结果。

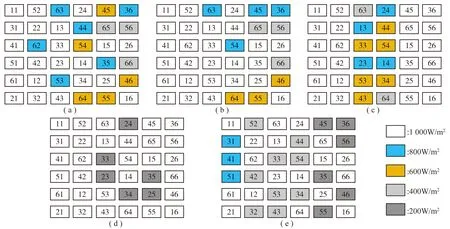
图10 Arrow So Du ku重构后阴影分布情况

利用Zig-zag进行重构之后,可以得到如图11所示的结果。

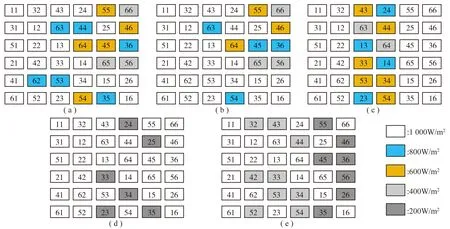
图11 Zig-zag重构后阴影分布情况

利用OEC奇偶重构法进行重构之后,可以得到如图12所示的结果。

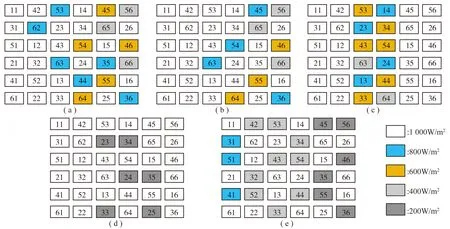
图12 OEC重构后阴影分布情况

利用OOEC方法进行重构之后,可以得到如图13所示的结果。

图13 OOEC重构后阴影分布情况

在上述五种阴影下,利用不同方法进行重构,重构前/后光伏阵列的PU输出特性曲线如图14～18所示。

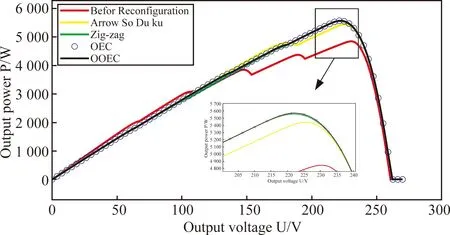
图14 梯形阴影

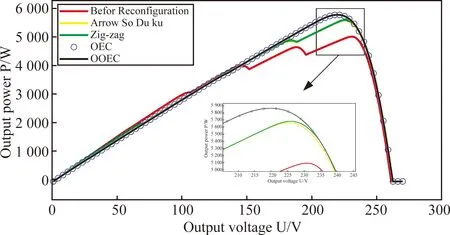
图15 三角形阴影

图16 竖长条形阴影

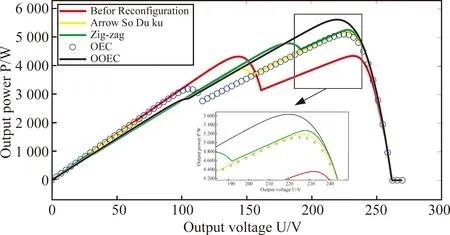
图17 局部阴影

图18 横长条形阴影

部分阴影遮挡情况下,光伏阵列重构前的PU特性曲线呈现:多峰值,平滑度不高,最大输出功率不高的特点。利用不同重构方法进行重构后,对于光伏阵列输出功率均有提升,在梯形阴影,三角形阴影情况下,使用OEC与OOEC完成重构后,最大输出功率相同。在竖长条形阴影情况下,使用Zig-zag、OEC与OOEC完成重构后,最大输出功率相同。

部分阴影遮挡情况下光伏阵列重构的失配损耗见图19。

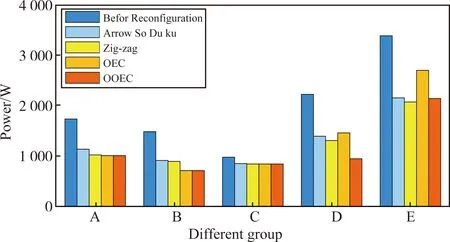
图19 部分阴影遮挡情况下失配损耗

如图20所示,失配损耗分为5组。组A代表梯形阴影情况,组B代表三角形阴影情况,组C代表竖长条形阴影情况,组D代表局部阴影情况,组E代表横长条形阴影情况。由图可见,利用OOEC方法进行光伏阵列重构在大部分情况下失配损耗最低。

图20 动态阴影和普通阴影遮挡加阵列损坏情况

(2) 阴影加阵列损坏情况。光伏阵列重构前,动态阴影和阴影遮挡加光伏阵列损坏情况如图20所示,图20(a)表示动态阴影加阵列损坏第一阶段,图20(b)表示动态阴影加阵列损坏第二阶段,图20(c)表示动态阴影加阵列损坏第三阶段,图20(d)表示梯形阴影遮挡加光伏阵列损坏情况,图20(e)表示三角形阴影遮挡加光伏阵列损坏情况。

利用Arrow So Du ku进行重构之后可以得到如图21所示的结果。

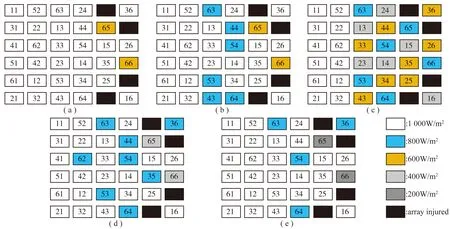
图21 Arrow So Du ku重构后阴影及故障阵列分布情况

利用Zig-zag进行重构之后可以得到如图22所示的结果。

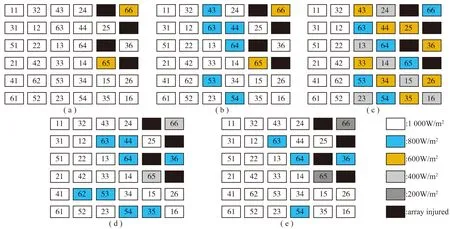
图22 Zig-zag重构后阴影及故障阵列分布情况

利用OEC奇偶重构法进行重构之后可以得到如图23所示的结果。

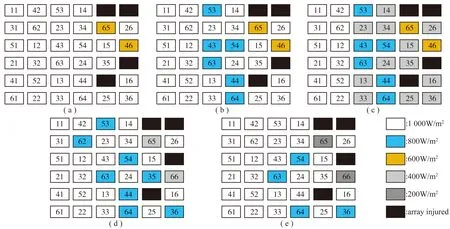
图23 OEC重构后阴影及故障阵列分布情况

利用OOEC方法进行重构之后可以得到如图24所示的结果。

图24 OOEC重构后阴影及故障阵列分布情况

上述五种情况,利用不同方法进行重构,重构前/后光伏阵列的PU输出特性曲线图25～29所示。

图25 动态阴影阶段1加阵列损坏

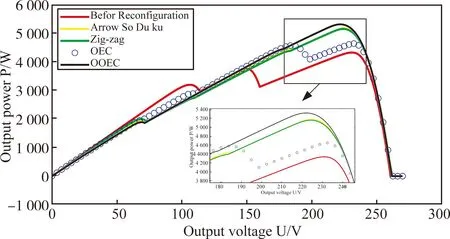
图26 动态阴影阶段2加阵列损坏

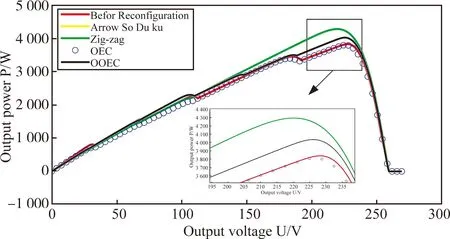
图27 动态阴影阶段3加阵列损坏

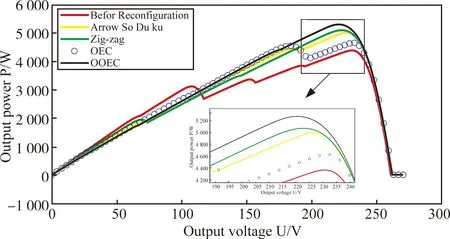
图28 梯形阴影加阵列损坏

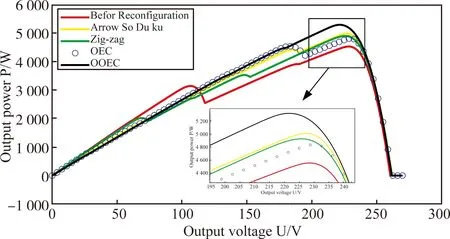
图29 三角形阴影加阵列损坏

阴影加阵列损坏情况下光伏阵列重构的失配损耗见图30。失配损耗分为5组。组A代表动态阴影阶段1加阵列故障情况,组B代表动态阴影阶段2加阵列故障情况,组C代表动态阴影阶段3加阵列故障情况,组D代表梯形阴影加阵列故障情况,组E代表三角形阴影加阵列故障情况。可见,利用OOEC方法进行光伏阵列重构在四种情况下有着最低的失配损耗。

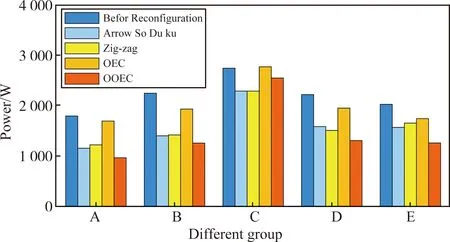
图30 阴影加阵列损坏情况下失配损耗

对失配损耗进行图示说明后,对其余三个指标进行说明,如表3,表4,表5所示。针对行电流可以理论上计算如

IRW1=A11I11+A12I12+A13I13+A14I14,

(6)

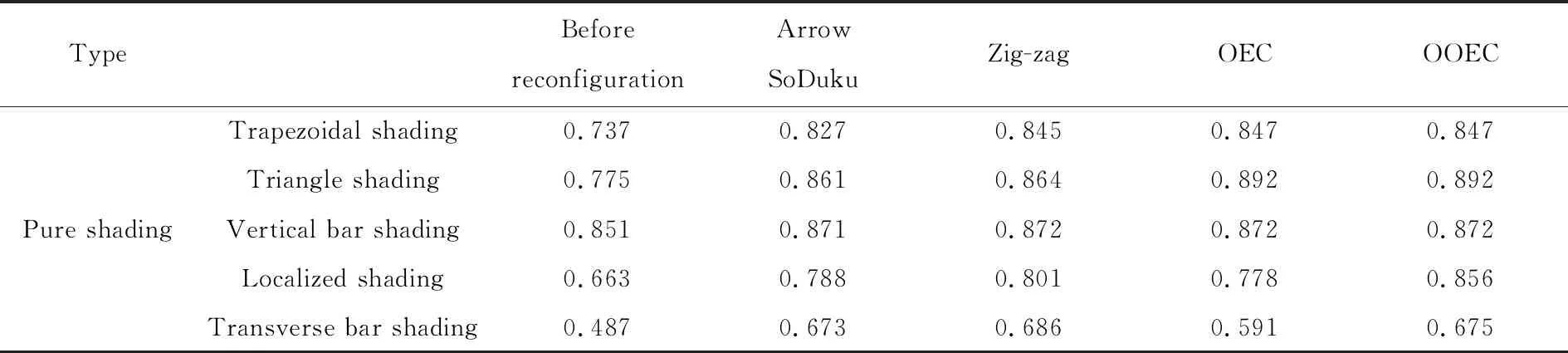
表3 性能比(纯阴影)

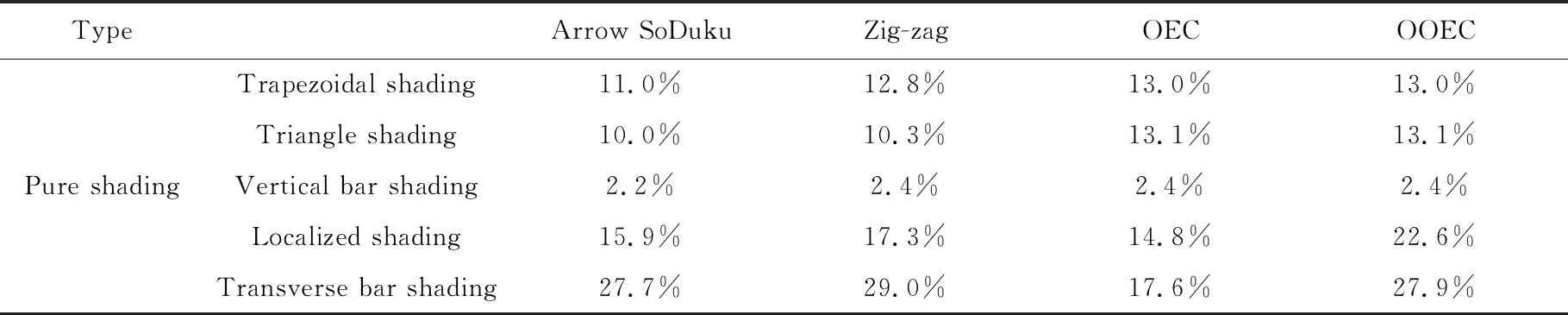
表4 功率增强百分比(纯阴影)

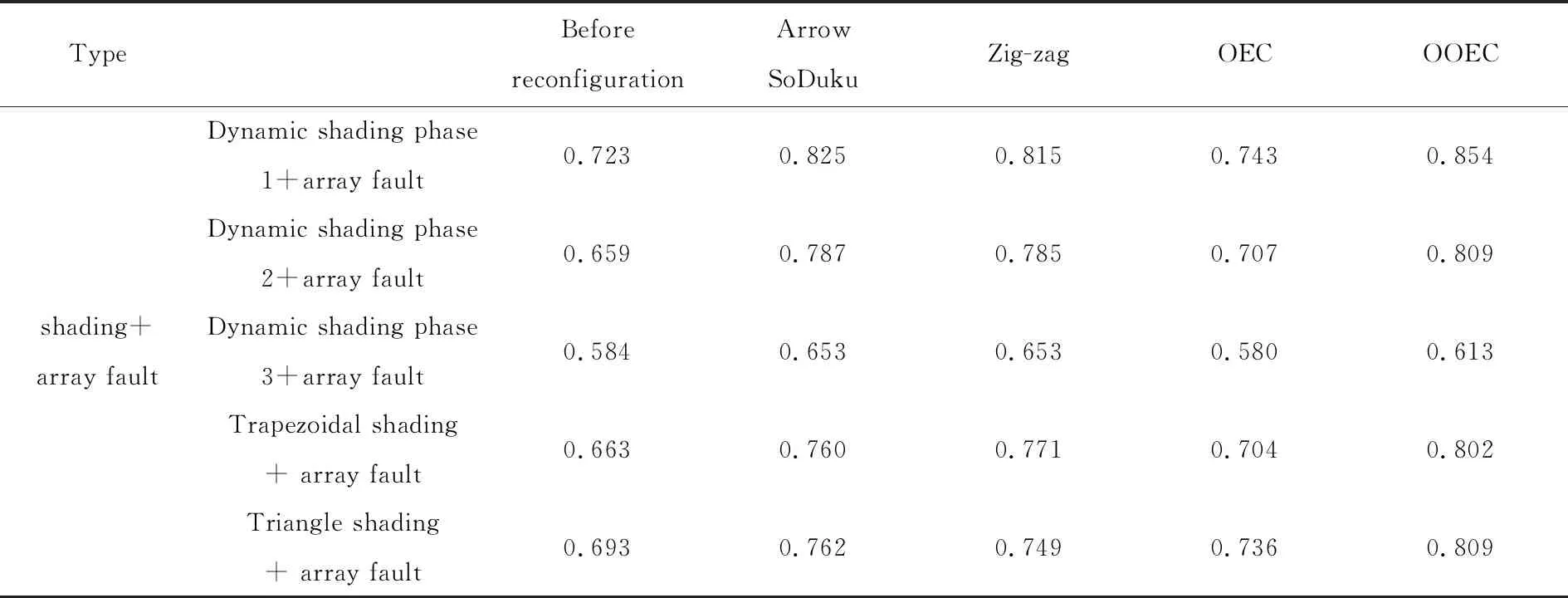
表6 性能比(阴影+阵列故障)

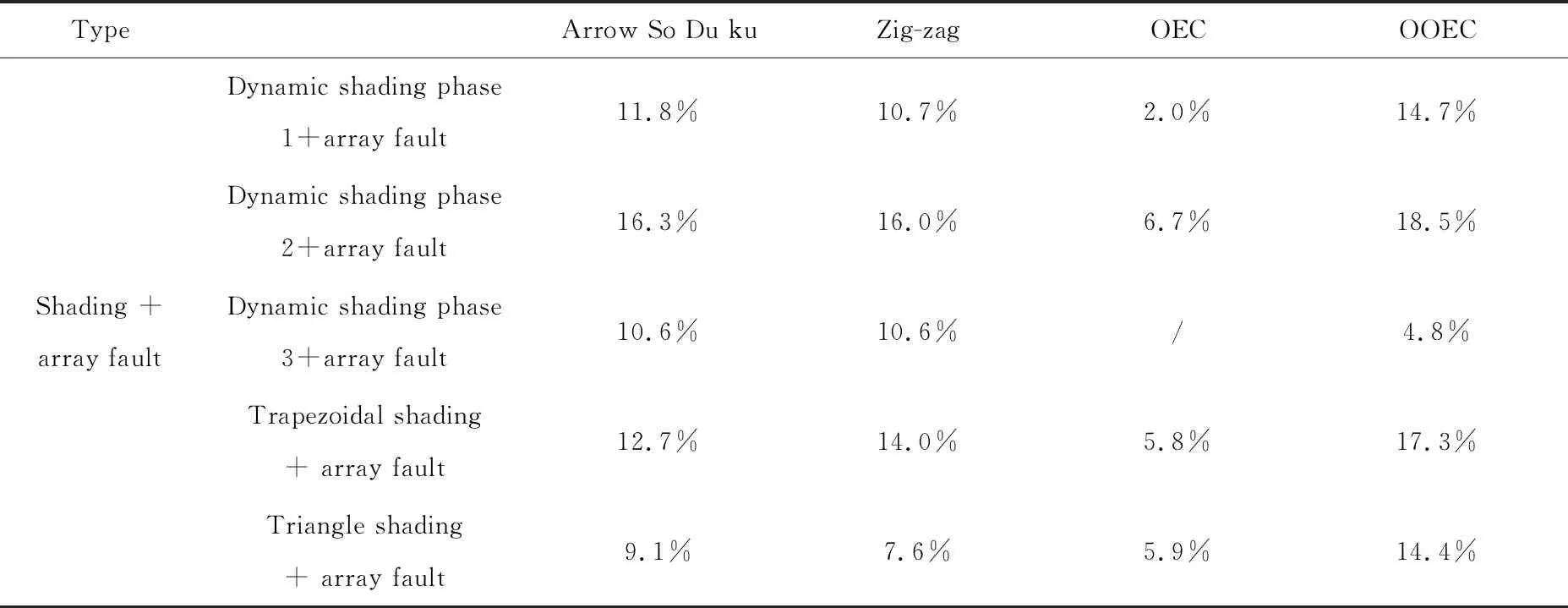
表7 功率增强百分比(阴影+阵列故障)

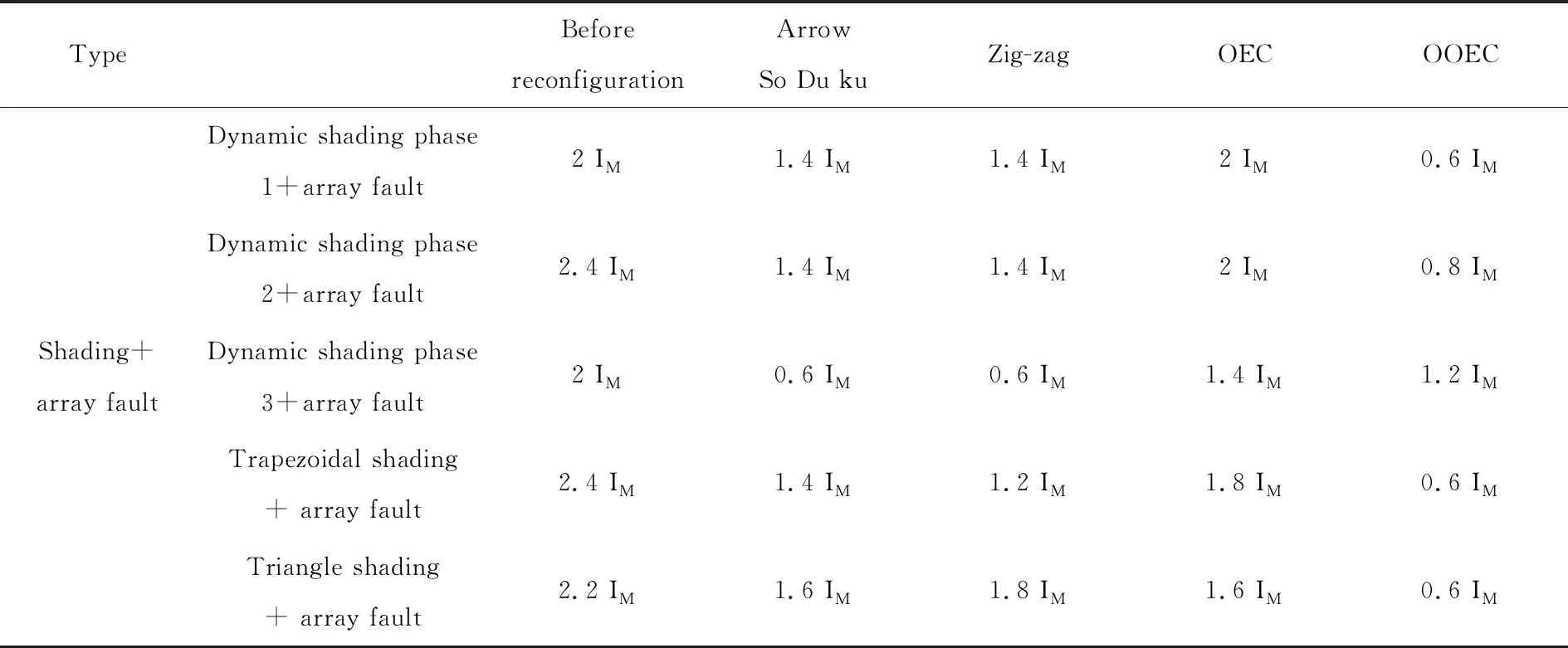
表8 均衡指数(阴影+阵列故障)

式中A11为第一行第一列的光伏阵列所接收到的光照强度与标准光照强度的比值,依此类推。

4 结果与讨论

分析仿真实验结果,通过所列表格以及功率电压输出图可见:利用OOEC进行重构整体效果好于重构前,OEC,Arrow SoDuKu以及Zig-zag的效果。

(1) 从功率方面来看,利用OOEC进行重构之后,所得到的功率电压输出曲线比其余的方法进行重构后得到的曲线要更加光滑。在纯阴影的5种情况下,OOEC在4种情况下输出功率最高;在梯形阴影,三角形阴影,局部阴影情况下,OOEC和Zig-zag以及OEC最大输出功率一致,这是因为在这时候利用OEC以及Zig-zag已经达到了很好的重构效果;在阴影加阵列故障的5种情况下,OOEC在4种情况下输出功率最高,并且输出中没有过多的局部峰值。

(2) 从性能比来看,利用OOEC进行重构后,在纯阴影情况下分别是0.847,0.892,0.872,0.856,0.675;在阴影加阵列故障情况下分别是0.854,0.809,0.613,0.802,0.809。在大多数情况下均超过了0.8,此时对于光伏阵列输出有着很好的效果。

(3) 从功率增强百分比来看,利用OOEC进行重构后,在纯阴影情况下相较重构前分别提升了13.0%,13.1%,2.4%,22.6%,27.9%;在阴影加阵列故障的情况下相较重构前分别提升了14.7%,18.5%,4.8%,17.3%,14.4%。证明了利用OOEC进行重构始终在功率方面保持一个正面的影响。

(4) 从均衡指数方面来看,利用OOEC进行重构后,只有一种情况下均衡指数超过了IM,而其余的重构方法则显得不够稳定。

5 总结

针对6×6光伏阵列提出了一种OOEC方法来对光伏阵列进行重构,该重构技术能够有效增强阵列的功率和能量生成,与传统的OEC奇偶重构法相比多了一列自由重构模块,加入了AAR技术的思想,能够更好地应对多种类型的情况,也能够应用于各种大小的光伏阵列。此方法的重构成本相对于动态重构较低,同时也可以有效改善光伏阵列在各种情况下的多峰值现象,为后续进行光伏阵列的最大功率追踪提供了一个很好的基础。同时与Arrow So Du ku,Zig-zag,OEC三种方法进行了对比,由仿真实验,通过对失配损耗、性能比、功率增强百分比、电流变化指数四种评价指标的计算,发现OOEC方法能够应对更多类型的情况,由于自由模块的存在,更适应阴影的变化等。具体结果总结如:(1) 常规的静态重构方法比动态重构方法控制简单,但是在现场应用中难以实现。大多数光伏阵列的安装是固定的,很难改变光伏阵列的位置。本文所提出的有关自由重构模块的开关结构,可以很好的解决常规静态重构方法的不足。(2) 由本文所提及的评价标准综合考量可知,OOEC方法对于光伏阵列重构有着更好的性能,更加契合现实环境,能够应用在光伏建筑以及小型的光伏电站之中。(3) 所提出的重构技术有一定的经济效益,可实施性高,可以进行实际应用。因此,本文所提出的重构技术是合理的,可以有效地分散阴影并且在阵列损坏情况下也有着良好的表现。此外,这项工作可以扩展和探索不同的静态重构方法。