借助化归思想，解答数学难题

喻成刚

【摘要】在高中数学解题教学中，学生会遇到一些难题，对学生学习效率有着较大的影响.为了提高课堂教学效率，教师应当注重数学思想的引入.化归思想作为重要的数学思想，引入高中数学课堂，能够提高课堂教学效率.同时，化归思想有利于学生数学难题的解答，帮助学生掌握数学解题方法，进一步强化学生思维能力.本文分析数学难题解题中化归思想的应用策略.

【关键词】高中数学；化归思想；解题策略

化归思想即转化与归结思想，是重要的数学思想与方法，核心是对未解决的问题进行转化.在高中数学解题中，无论是难还是易，常常会用到化归思想，如空间转化平面、多元转化少元、高次转化低次、复杂转化简单、一般转化特殊以及隐性转化显性等，通过这样化繁为简，有效解决数学难题.

1  空间转化为平面

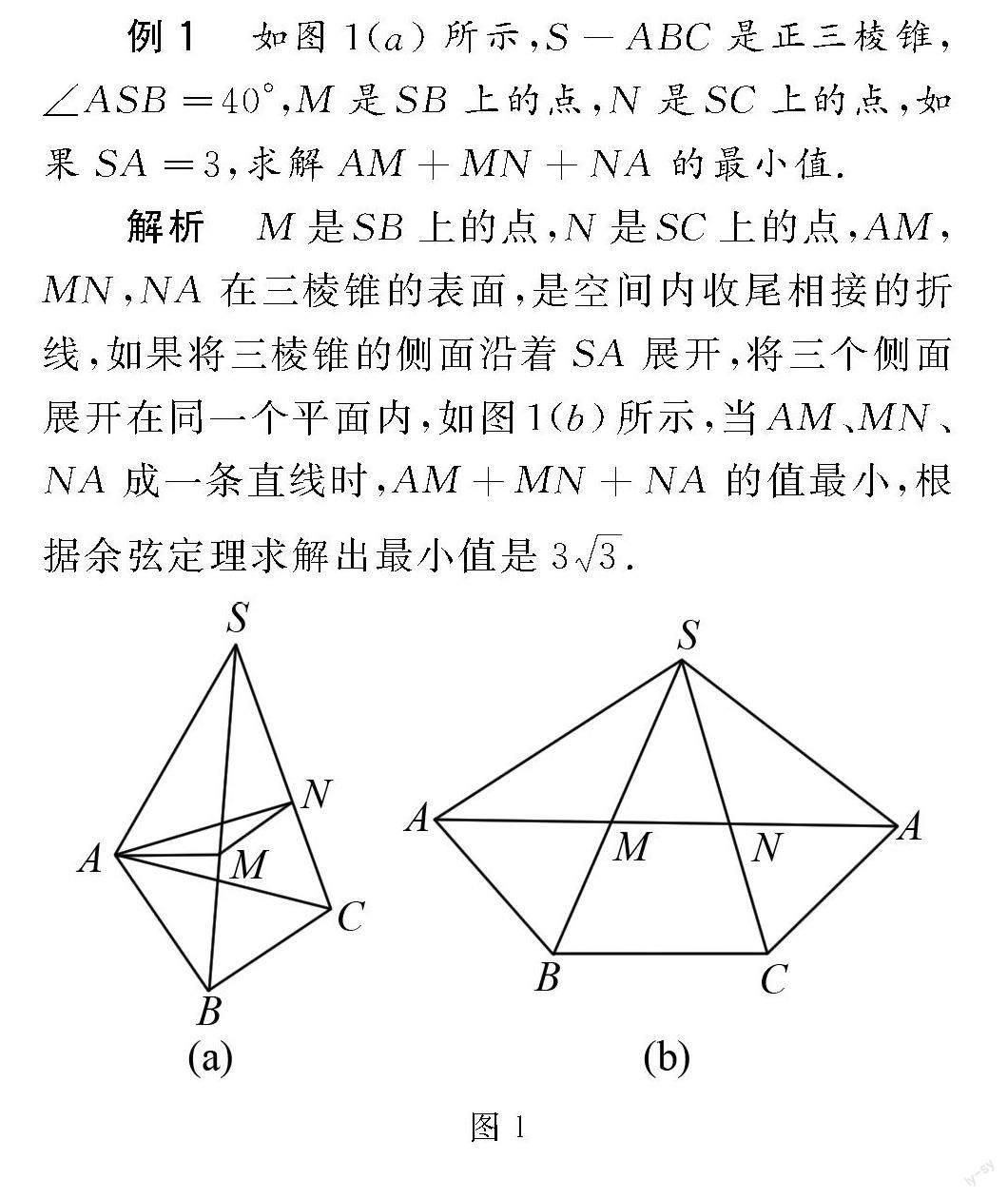
例1  如图1（a）所示，S－ABC是正三棱锥，∠ASB=40°，M是SB上的点，N是SC上的点，如果SA=3，求解AM+MN+NA的最小值.

解析  M是SB上的点，N是SC上的点，AM，MN，NA在三棱锥的表面，是空间内收尾相接的折线，如果将三棱锥的侧面沿着SA展开，将三个侧面展开在同一个平面内，如图1（b）所示，当AM、MN、NA成一条直线时，AM+MN+NA的值最小，根据余弦定理求解出最小值是33.

图1

2  高次转化为低次

例2  已知函数f（x）=ax3+bx2－3x，当x=±1时，函数取极值，讨论f（1）与f（－1）哪个为极大值，哪个为极小值.

解  根据函数f（x）=ax3+bx2－3x，

所以f′（x）=3ax2+2bx－3，

根据题意得f′（1）=f′（－1），

所以3a+2b－3=0，3a－2b－3=0，

所以a=1，b=0，所以f（x）=x3－3x，

f′（x）=3x2－3=3（x+1）（x－1），

令f′（x）=0，所以x=±1.

若x∈（－∞，－1）∪（1，+∞），则f′（x）＞0，所以f（x）在（－∞，－1）∪（1，+∞）是增函数.

若x∈（－1，1），f′（x）＜0，所以f（x）在（－1，1）上是减函数.

所以，f（－1）=2是极大值，f（1）=－2是极小值.

3  复杂转化为简单

例3  对于所有实数x，不等式x2log24（a+1）a+2xlog22aa+1+log2（a+1）24a2＞0恒成立，求a的取值范围.

解  设t=log22aa+1，

所以log24（a+1）a=3－t，log2（a+1）24a2=－2t，

所以原不等式可以转化为（3－t）x2+2tx－2t＞0恒成立，

因为对于所有实数x，不等式恒成立，

所以3－t＞0，Δ=4t2－4（3－t）＜0，

求解得出t＜0，

即log22aa+1＜0，

所以0＜2aa+1＜1，

得出0＜a＜1.

4  一般转化为特殊

例4  已知x，y∈R+，是否存在常数c使得不等式x2x+y+yx+2y≤c≤xx+2y+y2x+y恒成立？试证明.

解析  在解此題时，可以利用一般转化为特殊的方式，考虑不等式等号成立的情况，令x=y，所以得出23≤c≤23，所以c=23.

首先证明x2x+y+yx+2y≤23，

因为x，y∈R+，所以只需要证明3x（x+2y）+3y（2x+y）≤2（2x+y）（x+2y），

得出x2+y2－2xy≥0，

即（x－y）2≥0恒成立.

同理可以证明23≤xx+2y+y2x+y，

所以存在常数c=23使得不等式x2x+y+yx+2y≤c≤xx+2y+y2x+y恒成立.

5  隐性转化为显性

例5  解不等式|x2－10x+26－x2－2x+2|＜2.

解  原不等式可以转化为

y=1，|（x－5）2+y2－（x－1）2+y2|＜2，

解得y=1，（x－3）2－y23＜1，

所以3－233＜x＜3+233.

6  多元转化为少元

例6  在锐角△ABC中，如果cosA=cosαsinβ，cosB=cosβsinγ，cosC=cosrsina，求证：tanαtanβtanλ=1.

证明  在△ABC中，A+B+C=180°，

所以cos（A+B）=－cosC，

cosAcosB－sinAsinB=－cosC.

所以（cosAcosB+cosC）2=sin2Asin2B，

所以cos2A+cos2B+cos2C=1－2cosAcosBcosC，

代入已知条件，得出α、β、γ的关系：

cos2αsin2β+cos2βsin2γ+cos2γsin2α=1－2cosαcosβcosγsinαsinβsinγ，

两边同时除以cos2αcos2βcos2γ得出：

tan2βsec2γ+tan2γsec2α+ tan2αsec2β= sec2asec2βsec2γ－2tanαtanβtanγ，

因为sec2γ=1+tan2γ，

sec2β=1+tan2β，

sec2α=1+tan2α，

代换可以得出（tanαtanβtanγ－1）2=0，

所以tanαtanβtanγ=1.

7  结语

在高中数学难题解题中，利用化归思想，将复杂、困难问题转化成简单熟悉的问题.在化归思想应用时，应当避免硬套公式，需要灵活利用，仔细阅读题目，对题目条件和结论进行分析.同时，教师需要让学生做好日常学习积累，归纳总结化归思想应用方法，提高学生的难题解题能力.

参考文献：

［1］沈月红.拨云见日终有时，化归解题醉晴空——化归思想在高中数学解题过程中的应用方法分析［J］.数学学习与研究，2022（34）：17-19.

［2］彭鲁.由难化易，由繁化简——高中数学解题过程中化归思想的应用［J］.新教育时代电子杂志（学生版），2020（12）：116.

［3］谭谢燕.巧用化归思想 解答数学难题［J］.数理天地（初中版），2022（05）：79-81.