弱纹理环境下融合点线特征的双目视觉同步定位与建图

龚 坤，徐 鑫，陈小庆，许悦雷*，张兆祥

（1.西北工业大学 无人系统技术研究院，陕西 西安 710072；2.中国人民解放军军事科学院 国防科技创新研究院，北京 100850）

1 引言

目前，自主移动机器人在完全未知且拒止的环境中，需要依靠对周围环境的感知来确定自身位置以实现自主导航。这种方法被称为同步建图与定位（Simultaneous Localization and Mapping，SLAM）［1］。SLAM 主要分为激光SLAM与视觉SLAM［2-3］。在室外环境中，由于光线的干扰，一般采用激光SLAM 为移动机器人提供高精度导航信息，如自动驾驶车辆等。而在室内环境下，扫地机器人等已开始采用视觉SLAM［4］。目前，视觉SLAM 作为一种低成本的定位方案，引起了广泛的关注［5-6］。

视觉SLAM 依据所采用的图像特征不同，可分为基于特征点的方法，如ORBSLAM［7-9］，VINS［10］等，以及基于直接法或者半直接法，如DSO［11］，SVO［12］等。其中，直接法以及半直接法需要依赖灰度不变假设，因此对光线的影响较为敏感［13］；基于特征点的方法（例如ORB 特征点）能够提取具有尺度不变性和旋转不变性的特征点，但对环境纹理的要求较高，如果特征点较少或者移动速度较快，特征点容易丢失［14］。2017年，PL-SLAM 系统［15］被提出，相比基于ORBSLAM 算法，它是第一个使用点特征和线特征进行融合的双目SLAM 系统，且在光束（Bundle Ajustment，BA）优化阶段，同时考虑两种特征约束来优化相机位姿，从而提高了算法的精度和稳定性。然而，由于特征数量的增加，特征提取、匹配和优化部分的计算时间增加，导致PL-SLAM系统的实时性较差。

Company-Corcoles 等［16］提出了一种基于RGB-D 的视觉里程计称为MSC-VO。该方法结合ORB 特征点和LSD 线特征［17］，用于估计相机的姿态。MSC-VO 通过估计空间中的曼哈顿轴以及点和线的重投影误差，利用局部地图进一步优化相机的姿态。这种综合特征的使用和局部地图的优化有助于提高相机姿态估计的准确性和稳定性。贺一家博士团队［18］在VINS-mono［10］的基础上，通过添加LSD 线特征跟踪提出了一种PL-SLAM。他们结合VINS-mono 的单目视觉惯性里程计和LSD 线特征跟踪，以实现更准确和稳定的SLAM。这种改进在保持VINS-mono 优势的同时，通过引入线特征跟踪提高了系统的稳定性。

在弱纹理环境下，尤其是白墙较多的走廊，尽管更多的特征可以提高算法的稳定性，但也会限制算法的实时性。原本对于前端点特征的提取已经很耗时，再加上线特征的提取和匹配，SLAM 系统的实时性难以保证。针对此问题，Gomez 等［19］在SVO［12］的基础上提出了PL-SVO，引入了一种快速跟踪线段的方法。将半直接方法扩展到线特征的情况下，通过作为稀疏-直接运动估计的隐式结果来执行快速线段跟踪，并利用这种稀疏结构来消除线段检测。吴毅红团队［20］提出了一种基于IMU-KLT 预测的高效线段跟踪方法，通过IMU 的预测以及光流信息对线段位置进行预测，加快匹配速度，线段的跟踪时间仅需要3.7 ms。然而，以上方法仅针对单目线段跟踪展开研究，并未探索线段提取的质量问题。此外，在双目情况下如何实现快速的线段匹配和三角化的研究仍然较少，目前主要依赖于传统的LSD+LBD［21］方法，但该方法的实时性能较差。

本文在前人研究的基础上，提出一种融合点线特征的双目视觉SLAM 系统，重点改进了线特征的提取和匹配过程。考虑到高质量和稳定性的线特征对SLAM 系统的贡献更大，本文对LSD 线特征提取方法进行改进，通过长度和梯度抑制策略以及短线合并等方法进一步提高线段提取的质量。另外，本文还引入了一种基于几何约束的快速线段三角化方法，通过引入区域约束、邻域约束和平行约束构建代价函数，并将线段匹配问题转化为优化问题。利用L1 范数的稀疏解求得最优匹配，并通过线特征的重投影误差进行线段的非线性优化，从而提高线段三角化精度。在公开数据集和自建数据集上验证了本文所提方法的先进性，并将它应用于实际的双目视觉SLAM 系统中。实验结果表明，该方法的定位精度优于现有算法，验证了其在实际应用中的有效性。

2 原 理

2.1 双目视觉SLAM 系统框架

本文所提出的融合点线特征的双目视觉SLAM 系统框架主要分为跟踪线程和局部建图线程两个部分，其框架示意图如图1 所示。

图1 融合点线特征的双目视觉SLAM 系统框架Fig.1 Framework of binocular vision odometer system integrating point and line features

在跟踪线程中，双目图像作为输入，首先对其利用多线程的方式分别对左右目图像提取点特征与线特征，并利用特征匹配进行点线特征的三角化；在位姿估计中，通过对点线特征的持续跟踪，构建点线特征的联合重投影残差，并利用非线性优化求解位姿，如下：

局部建图线程通过具有共视关系的多个关键帧来维护一个共视窗口进行后端位姿图的局部优化，主要通过将地图中的点特征以及线特征的重投影误差Epi，Elj作为相机位姿约束，以及曼哈顿轴约束进行联合BA（光束平差法），对跟踪线程得到的相机位姿进行进一步优化，从而消除累积误差，如式（2）所示［16］：

其中：Mj表示对地图线特征估计所得的曼哈顿轴，E||j，Mj代表曼哈顿轴Mj∈M相对于局部地图中线特征j的误差项。

2.2 基于改进LSD 的线特征提取方法

本文平衡考虑精度和速度，采用LSD 线特征提取方法。然而，由于LSD 算法提取的无效线特征数量较多，提取和匹配的时间成本较高。此外，高质量的特征更容易稳定地跟踪，并对定位算法做出更大的贡献。如果直接将LSD 算法应用于视觉SLAM 系统中，仍然会面临一些问题需要解决。因此，本文提出了一种改进的LSD 线特征提取方法，通过对线特征的梯度和长度进行抑制，抑制了一些梯度较小且长度较短的线特征的产生。同时，在局部优化过程中考虑平行和垂直约束以及曼哈顿轴的估计，保留了相互平行和垂直的线特征。这样做有利于提高线特征的质量，并为后续的线特征匹配和定位过程提供更好的约束条件。

对于一些短线特征可以通过判断是否满足短线合并条件从而进行线段的合并，从而成为质量更高的线特征。这种合并操作不仅可以减少线特征的数量，还能加快匹配和定位的速度，并降低定位算法的漂移风险。

假设Ln，Lm是需要合并的两条线特征向量，故其合并条件为在图像坐标系下满足平行约束，且两者左端点和右端点存在一定距离，由于斜率可能不存在，故采用向量夹角的余弦值作为判定条件，合并条件即：

其中：λmin为平行判定阈值（根据多次平行特征余弦值计算实验。由于特征提取误差导致其余弦值往往无法达到1，一般在0.999x以下的数量级，故确定为0.999），distance（）代表两直线端点的最短距离，Ln.length 代表Ln的长度。综上所述，基于改进LSD 的线特征提取算法的伪代码描述如下：

在第3，4，5 步中，将梯度不明显的像素和长度较小的矩形区域进行剔除，并将剩下的未存在于矩形区域的每个像素分配到最近的直线区域，这有助于抑制一些梯度较小且长度较短的线特征的产生。在第6 步中，对长度小于阈值的线特征，只保留相互平行或垂直的线特征，并判断是否满足合并条件，从而将短线特征合并成质量更高的线特征。

2.3 基于几何约束的快速线段三角化

传统方法下，帧与帧之间的线特征的三角化方法主要为首先提取两帧之间LSD 线特征然后利用LBD 描述子进行匹配，从而得到归一化平面上线对的直线方程，若已知相机中心C1，C2在世界坐标系中的位置，便可得到线与相机中心的两个平面方程，通过平面方程的交线便可求出线特征的世界坐标［16］，示意图如图2 所示。

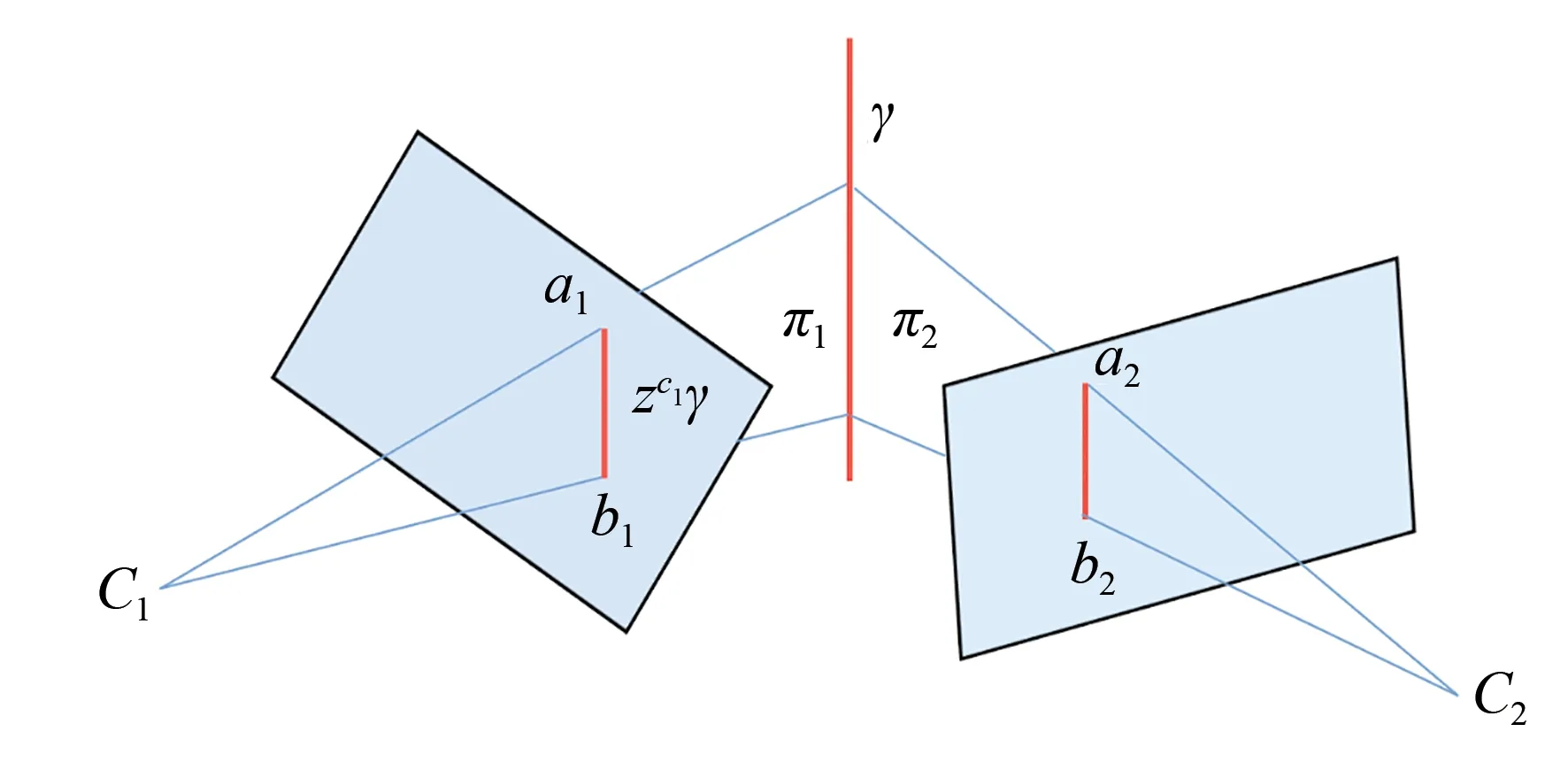
图2 线特征三角化方法Fig.2 Line feature triangulation method

本文针对双目视觉的线特征三角化问题，提出一种基于几何约束的线特征三角化方法。针对线特征的匹配问题，传统的基于LBD 描述子的匹配方式应用于双目线特征匹配，计算描述子复杂且匹配时间较长，不适用于弱纹理环境。双目平行线特征匹配和三角化方法却能提高线特征的匹配效率，其示意图如图3 所示。

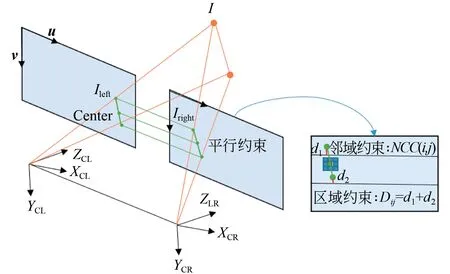
图3 基于几何约束的双目线特征三角化方法示意图Fig.3 Schematic diagram of binocular line feature triangulation method based on geometric constraints

此外，双目图像经过立体校正和去畸变处理后，双目图像中的像素点在对应的行上具有严格的一一对应关系。利用极线约束，两幅图像中的对应线在同一水平线上，因此线对应满足区域约束。如图3 所示，区域约束的应用过滤掉大部分无关的线特征，从而加快了匹配速度。右目匹配线段应处于区域内或与区域相交，故定义区域约束Dij，将线段lk={sk，ek}，sk和ek分别为线段的两端点，故区域约束Dij如下：

鉴于平行约束与区域约束仅针对线特征本身，并未利用其邻域信息，本文基于传统的NCC匹配方法提出一种线特征的邻域约束，即取左目线段的中心构建3×3 邻域匹配窗口Wp，并通过建立目标函数来对右目线特征的匹配窗口进行度量相关性，如式（7）所示：

其中：d为左右目匹配中心区域的横坐标之差，Ii(x，y)代表左目邻域窗口Wp中的像素灰度值，Ij(x+d，y)代表右目匹配窗口Wp中的像素灰度值。若NCC=-1，表示两个匹配窗口完全不相关；若NCC=1，则表示两个匹配窗口相关程度非常高。令Nij=(1-NCCij)/2，故可定义左右目线对的匹配代价向量Qij为：

其中Uij为线段的长度约束，设两线段长度的比值为u，故Uij=|u-1|。若定义在左目区域约束内的所有线段的代价向量为Ai={Qi0，Qi1…，Qin}，由于双目线特征匹配问题具有奇异性，即左右目线段都是唯一对应的，若设其匹配向量xi={xi0，xi1…，xin}，其中xij表示线对匹配成功则为1，反之则为0。进一步建立线性约束Ai xi=b，其中b=[0 0 0 0]代表匹配误差，保证其奇异性，且匹配向量xi归一化后所有分量之和为1。因此，在上述约束条件下，将线段匹配问题转化为优化问题，利用L1 范数得到最优解的稀疏表示［23］：

初始值为x0={1，0…，0}，采用牛顿高斯法求得其数值最优解后，将xi进行归一化，xi中的最大分量xim代表两线段的相似性最大，即为查询线段的最佳匹配。

在双目线段匹配成功后，本文采用一种简单而有效的方法进行线特征的三角化。通过左目线段端点纵坐标的横线与右目匹配线段的交点，可以确定右目匹配线段的端点，从而完成线特征的三角化。此外，本文还借鉴文献［16］中RGBD相机的线特征优化方法，对双目三角化得到的线特征进行了非线性优化，利用线特征的重投影误差求得最优解。其优化公式为：

其中：Ek，o为归一化线与平行关联线段之间的夹角的正弦，ρ为减少异常值影响的Huber损失函数。

3 实 验

3.1 线特征提取与匹配

线特征提取与匹配实验设备如图4 所示，弱纹理图像采集设备采用小觅双目相机（S1030），分辨率为1 344×376，焦距为2.1 mm，基线长度为12 cm，帧率为30 Hz，自建数据集场景为弱纹理室内走廊环境，场景中仅存在白墙和门窗，如图5 和图6（a）所示，距离全长为91 m 左右，录制时长为216 s，图像数量为2×6 684 张。

图5 线特征提取算法对比Fig.5 Comparison of line feature extraction algorithms

图6 双目匹配算法在弱纹理数据下的对比Fig.6 Comparison of binocular matching algorithm under weak texture data

本文将所提出的线特征提取与匹配方法与目前已有方法进行对比，线特征提取算法与原本的LSD 算法进行对比，结果如图5 所示。

由图5 可知，原始LSD 算法提取的线段分布较为集中，短小线段居多，且大部分梯度不明显；相比之下，改进LSD 线特征提取算法提取的线段质量明显高于原LSD 算法，且线特征大多为水平和竖直线段，为曼哈顿轴估计和基于线特征的位姿约束提供了更强的约束信息，更容易被跟踪。

线特征匹配实验中，将本文所提基于几何约束的线特征匹配算法与传统的基于LBD 描述子方法进行对比。为了评估算法性能，本文使用的双目匹配数据集为公开双目数据集（室内Euroc数据集［24］、室外KITTI 数据集［25］）与自建弱纹理数据集。图6 展示了在弱纹理图像数据上进行的线特征匹配结果（彩图见期刊电子版）。

在线特征提取方面，如图6（a）和6（c）中红色圆圈所示，LSD 算法提取的线特征大多具有较短的长度和较小的梯度，无法进行有效的匹配，因此被认为是无效特征。相比之下，本文提出的改进线特征检测算法（如图6（b）和6（d）所示）明显提高了线特征的质量，无效线特征的数量较少。在线特征匹配方面，本文所提方法基本无错误匹配，而基于LBD 描述子的方法存在多处错误匹配，如图6（a）和6（c）中红色线段所示，匹配精度明显高于LSD+LBD 算法。为了定量评价双目线特征匹配算法的精度，一般认为投影误差小于5 个像素为正确匹配。实验中，使用正确匹配的数量与匹配总数量之比来评估算法平均实验的匹配精度［20］。

本文所用实验平台CPU 为i5-4690，系统为ubuntu18.04；共进行20 组实验，每次实验取数据中跨度较大的实验场景，平均实验匹配精度与匹配时间如表1 所示。

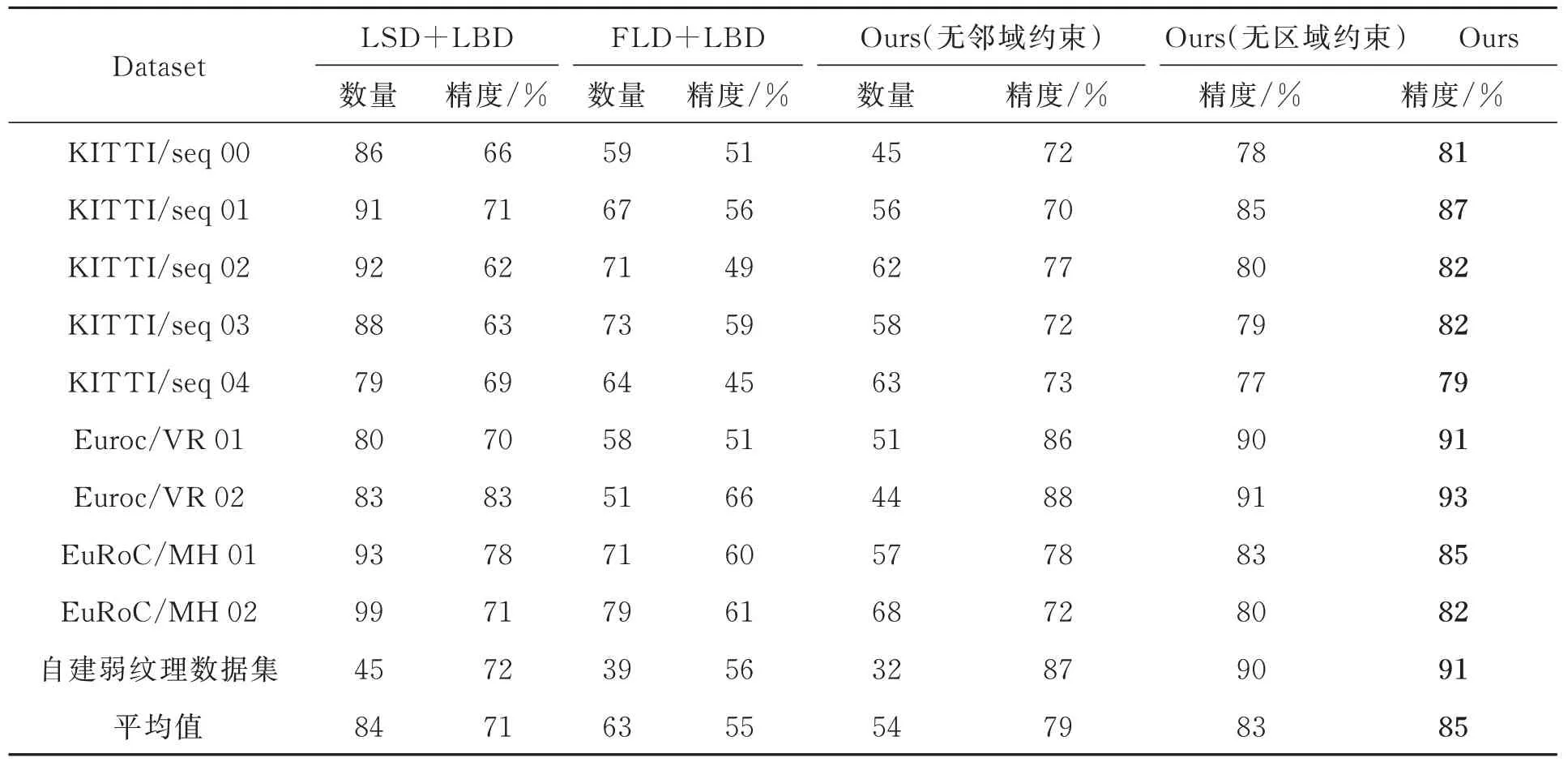
表1 该方法与基于LBD 的线特征匹配方法对比Tab.1 Comparison between proposed method and line segment matching method based on LBD

表1 展示了本文所提算法与现有算法在公开数据集以及自建弱纹理数据集上的性能。首先，在线特征检测数量方面，LSD 算法的平均检测数量最多为84，FLD 算法平均检测数量为63。虽然本文所提算法最少为54，但在匹配精度方面，基于LBD 描述子的线特征匹配方法中，LSD 算法的平均匹配精度为71%，FLD 的平均匹配精度为55%，而本文所提方法的平均匹配精度为85%，优于其他两种方法。这主要归因于本文方法提取的线特征质量更高，并且通过双目的几何结构约束，每条线特征具有唯一的极大值解。在结构约束消融实验的对比中，当缺少邻域约束时，平均精度为78%，减少6%，而缺少区域约束为83%，减少2%，可看出邻域约束的作用大于区域约束，也证明了两种约束的有效性。

表2 比较了3 种不同方法的线特征平均提取时间以及匹配时间。其中，线特征提取时间是指两张图片的线特征提取时间，匹配时间则是指描述子的计算时间与匹配时间之和。在线特征提取方面，FLD 的提取速度最快，仅需18.5 ms，LSD 的线特征提取速度最慢，需要34.2 ms，本文所提出的算法的线特征提取速度居中为33.1 ms。在匹配时间方面，本文算法的线特征匹配时间仅需7.4 ms，而其他两种算法的匹配时间分别需要17.5 ms 和15.3 ms。这表明基于几何约束的线特征匹配方法比基于描述子的匹配方法具有更快的匹配速度。

表2 不同算法的时间性能比较Tab.2 Comparison of time consumption of different algorithms（ms）

综上所述，本文提出的基于几何约束的线特征匹配方法在精度和时间方面均表现出色，具有较高的实用性和效率。该方法能够提供精准的线特征匹配结果并在较短的时间内完成匹配，在双目视觉SLAM 系统中具有很大的应用潜力。

3.2 SLAM 建图与定位实验

本文将线特征检测和线特征快速三角化方法到双目视觉SLAM 系统中，提出一种点线特征融合的双目视觉SLAM 系统。为了评估该系统的性能，选择弱纹理的走廊和楼梯场景作为测试场景进行了对比实验。将本文方法与基于点特征的双目视觉SLAM 系统（ORBSLAM2 算法）进行对比，它们的建图和定位效果如图7 所示。

图7 改进双目点线融合视觉SLAM 与ORBSLAM2 算法建图与定位效果对比Fig.7 Comparison of image construction and positioning effects between improved binocular point line fusion visual SLAM and ORBSLAM2 algorithms

从图7（a）可以看出，基于点特征的ORBSLAM2［7］算法在转弯时由于特征缺失发生了轨迹漂移导致最终与起点发生重大偏离，而在图7（b）中则直接导致特征跟踪失败，算法失效。而点线融合双目视觉SLAM 系统在走廊和楼梯场景下产生的轨迹依然平滑，不存在轨迹漂移以及跟踪失败的现象，且最终成功回到起点，进一步证明本文所提算法的抗干扰能力更强，且本文算法在CPU 为i5-4690，系统为ubuntu18.04 的电脑主机上的平均运行帧率达到18.1 frame/s，满足实时性要求，具有更强的实用性能。为了进一步验证算法的先进性，将它与已有的基于点线融合的PL-SLAM［15］以及先进的ORBSLAM3［9］进行对比，它们的轨迹如图8 所示。

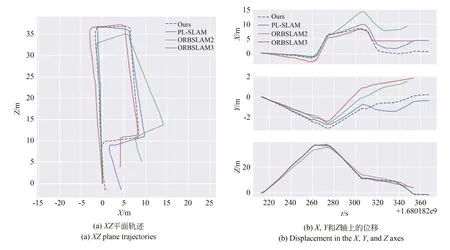
图8 四种算法的轨迹对比Fig.8 Trajectories comparison of four algorithms

图8 展示了4 种算法在具有挑战性的长方形环形走廊场景下的定位轨迹.从图8（a）可以观察到，本文所提出的改进算法是唯一成功回到起点形成闭环的算法，其他两种算法则无法完成闭环，而ORBSLAM2［8］，ORBSLAM3［9］由于特征缺失也未触发回环。以回到起点的距离作为误差判定，本文所提算法、ORBSLAM2［8］，ORBSLAM3［9］，PL-SLAM［15］的定位误差分别为1.24，7.49，6.36 和3.67 m。实验结果表明，该算法在弱纹理环境下的定位误差较小，相对于ORBSLAM2［8］，ORBSLAM3［9］算法，其精度分别提高了6.04 倍和5.13 倍；相对于PLSLAM［15］算法，其精度提高了2.96 倍。因此，在具有挑战性的弱纹理环境下，除了追求更多的特征之外，还需要确保特征的质量和稳定性，并提高线特征匹配的精度，以进一步提高定位的准确性。

4 结论

针对室内弱纹理环境下视觉SLAM 出现轨迹漂移等问题，本文提出了一种融合点线特征的双目视觉SLAM 系统，针对双目视觉SLAM中线特征提取与匹配问题进行研究，提出了一种基于改进的LSD 线特征提取方法，并在此基础上提出了一种基于几何约束的快速线特征三角化方法。实验结果表明，该方法在多个数据集上的表现都优于传统的LSD+LBD 方法，在室内弱纹理场景下的平均匹配精度达到91.67%，平均匹配时间为7.4 ms。双目视觉SLAM 系统的定位误差为1.24 m，其精度比ORBSLAM2，ORBSLAM3 算法高6.04 倍和5.13 倍，比PL-SLAM［算法高2.96 倍，具有很好的实用性和应用前景。未来，可以考虑更多的几何约束条件来进一步提高线特征匹配的准确性，或者探索更高效的线特征三角化方法，以及引入深度学习技术以提高系统的稳定性和泛化能力。