Service Function Chain Migration in LEO Satellite Networks

Geng Yuhui ,Wang Niwei ,Chen Xi,4 ,Xu Xiaofan,4 ,Zhou Changsheng ,Yang Junyi ,Xiao Zhenyu,*,Cao Xianbin

1 School of Electronic and Information Engineering,Beihang University,Beijing 100191,China

2 Key Laboratory of Advanced Technology of Near Space Information System,Ministry of Industry and Information Technology of China,Beijing 100191,China

3 Shanghai Key Laboratory of Satellite Network,Shanghai 201204,China

4 Shanghai Satellite Network Research Institute Co.,Ltd.,Shanghai 201204,China

Abstract: With the advancements of software defined network (SDN) and network function virtualization (NFV),service function chain (SFC) placement becomes a crucial enabler for flexible resource scheduling in low earth orbit(LEO)satellite networks.While due to the scarcity of bandwidth resources and dynamic topology of LEO satellites,the static SFC placement schemes may cause performance degradation,resource waste and even service failure.In this paper,we consider migration and establish an online migration model,especially considering the dynamic topology.Given the scarcity of bandwidth resources,the model aims to maximize the total number of accepted SFCs while incurring as little bandwidth cost of SFC transmission and migration as possible.Due to its NP-hardness,we propose a heuristic minimized dynamic SFC migration(MDSM)algorithm that only triggers the migration procedure when new SFCs are rejected.Simulation results demonstrate that MDSM achieves a performance close to the upper bound with lower complexity.

Keywords: network function virtualization(NFV);resource allocation;satellite networks;service function chain (SFC);SFC migration;SFC placement;soft-ware defined network(SDN)

I.INTRODUCTION

The satellite network has become an important supplement to the terrestrial counterparts,thanks to its capability of providing global coverage,high speed and broadband access.Among all types of satellite networks,low earth orbit (LEO) satellite networks have drawn more attention due to their lower delay and lower launch cost [1,2].However,it is also more likely to cause interruption of services and waste of scarce resources,due to the fast movement of LEO satellites[3].It is important to schedule computation and communication resources on demand to adapt to the dynamic network.In this regard,software defined network (SDN) and network function virtualization(NFV)are applied to make the LEO satellite network an open,flexible,and programmable platform.The heterogeneous resources are abstracted as a uniform resource pool,making it possible to allocate resources flexibly based on the real-time quality of service(QoS)requirements [4,5].After virtualizing the communication networks,various data services are realized by scheduling/placing the corresponding service function chains (SFCs) on demand,defined as a series of ordered virtualized network functions(VNFs).

When utilizing SDN and NFV in LEO satellite networks,SFC placement becomes a crucial problem,which refers to embedding VNFs with CPU and bandwidth resource requirements into proper physical servers to minimize end-to-end delay or deployment cost while guaranteeing QoS requirements.In some networks where the types of required SFCs are relatively fixed,the SFC placement and the resource allocation problem are solved sequentially.For example,the authors in [6] considered the basic deployment costs of VNFs and proposed a two-phase heuristic algorithm where SFCs were placed first in a cost-effective manner and then the placement of VNFs were adjusted according to the real-time network load.In[7],the authors placed SFCs by activating all types of VNF instances in each server in advance and adjusted VNFs based on the changes in traffic.Actually,in some real network scenarios,SFCs need to be placed in a first-come-first-serve manner on demand and scheduled in a more fine-grained way[8,9].In [8],the trade-off between the communication and computation resources was considered when placing SFCs,and a heuristic algorithm was proposed to minimize the total cost.In [9],a delay-aware SFC mapping algorithm was proposed to minimize the delay of SFCs and improve the utilization ratio of CPU and link resources simultaneously.Note that the works mentioned above [6-9] assume that requirements are known and conduct a one-shot greedy optimization of the placement of current SFCs.However,this may cause a decline in the subsequent SFC requests(SFCRs)when some nodes and links required by these SFCRs run out of resources.To accept more SFCs,the authors in [10] introduced the migration mechanism after SFCs were placed with resources allocated correspondingly for load balancing in the ground data center network.By ignoring the migration cost,a genetic algorithm was proposed to minimize the end-to-end delay and the network load changes simultaneously.A federated learning-based algorithm and a thresholdbased SFC migration policy were proposed in [11],to improve the resource utilization ratio and to raise the SFC acceptance ratio,respectively.However,the above mentioned methods[6-11]could not be applied to satellite networks directly,since they did not consider the limited bandwidth resources of satellite networks,which may cause the failure of SFC acceptance and migration.

Against this background,this paper studies the SFC migration problem and proposes a carefully designed online migration model where the requirements are unknown previously.To better depict the features of the real satellite networks,we assume that:

a) SFCRs arrive dynamically;

b) the resource and QoS requirements of SFCRs are known;

c) the total number of service types is limited but one VNF instance can only serve one SFCR.

The first assumption makes the model closer to the real service request situation of satellite networks.The second and third ones enable the bandwidth and CPU resources to be scheduled in a fine-grained manner and further save scarce bandwidth resources of the LEO satellite networks by reducing hops that data flows traverse.Given that the migration process may cause extra resource consumption when sparing room for new SFCs,we consider bandwidth cost in particular when formulating the migration cost model and study the trade-off between the migration cost and the total revenues.The main contribution of this paper can be summarized as follows.

1.We study SFC migration according to the realtime QoS requirements in the LEO satellite network.Specifically,the early-arrived SFCs are placed greedily at first and are allowed to migrate to different satellites when new SFCRs arrive.The destinations of migration are obtained by rescheduling all SFCs that have ever arrived to the system based on the real-time topology.An integer linear programming(ILP)problem is formulated to maximize the total profits brought by all accepted SFCs while incurring the minimum bandwidth cost of SFCs and migration cost.

2.We propose a heuristic algorithm called minimized dynamic SFC migration (MDSM) to address the formulated SFC migration problem.MDSM migrates the placed SFCs every time a new SFC is rejected,which is suitable for scenarios requiring quick decisions and infrequent migration.In particular,MDSM migrates SFCs occupying paths required by rejected SFCs to new paths incurring less extra cost.

3.Simulations have been conducted in the LEO satellite network under two scenarios with different levels of dynamics to verify the effectiveness of MDSM.The simulation results show that our proposed MDSM can reach a trade-off between the total revenues and the bandwidth cost,and its performance is close to the bound provided by the branch and bound algorithm while bringing lower computational complexity.

The remainder of this paper is organized as follows.In Section II,the system model and problem formulation are presented.The proposed MDSM algorithm is described in Section III.In Section IV,numerical results are shown to verify the effectiveness of MDSM.Finally,we give conclusions in Section V.

II.SYSTEM MODEL AND PROBLEM FORMULATION

In this section,we first describe the considered scenario and give an example to explain the necessity of migration in Section.2.1.Then,we present the system model from three aspects.Finally,the SFC migration problem is formulated.

2.1 Considered Scenario

This paper considers an LEO satellite communication network,composed of the satellite nodes,ground users,and the SDN controller/NFV orchestrator.The LEO satellites are equipped with computing and storage devices,which are interconnected with intersatellite links (ISLs).With the help of carried resources and ISLs,LEO satellites can hold VNFs for data processing.While it should be noted that the connections among them can be possibly interrupted/rebuilt due to the movement of LEO satellites.Given the limited computing capacities,the ground users do not hold VNFs themselves and need to send SFC requests(SFCRs)to the satellite network for processing.The SDN controller and NFV orchestrator are colocated on the ground to determine SFC placement and migration schemes.For tractable analysis,we divide the whole time horizon into several time slots and assume that new SFCRs arrive in the beginning of each time slot.The different VNF orders of SFCRs denote different types of services.For example,an SFC request for a company’s access is “Firewall→intrusion detection system(IDS)→Proxy”,where firewall needs to be executed before IDS and proxy[12].According to the characteristics of the real network [7],there should be a certain number of service types in the considered scenario.When an SFCR arrives at the network,required VNF instances are instantiated to exclusively serve this request and will not be shared by other SFCRs.

The migration may happen when the satellite nodes are overloaded with early-arrived SFCs and wanted by the newly arrived ones simultaneously.Figure 1 shows an example of SFC migration.There are two SFCs,i.e.,k1={S1→A →B →C →D1}andk2={S2→D →E →F →D1},which are generated at two different sourcesS1andS2,and reach the same destinationD1.In time slot 1,k1arrives in the system first and greedily consumes the current network resources to satisfy its QoS.VNF A ofk1is placed on LEO1,and VNF B and VNF C are placed on LEO2 according to some placement algorithm,without taking the requirements ofk2into account.Whenk2arrives at time slot 2,the optimal scheme is to place VNF D and E on LEO2 and place F on LEO3.However,there are not enough computing resources in LEO2,since VNFs ofk1have already been placed on it.In this case,k2may not be accepted,thus lowering the total profits.In such cases,in order to increase the total accepted SFCs,the VNFs placed on LEO2 can be migrated to idle satellites fork2.

In a word,SFC migration can adapt to real-time QoS requirements and accomplish more service requests,which is essential for the dynamic LEO satellite network.

2.2 System Model

When‖wtvt‖exceeds the maximum line of sight(LOS)distanceL(wtvt),the ISL of the satellites will be interrupted.Thus,a binary constantθt(i,j) is set to show whether link (i,j)∈LISLis connected att.When‖wtvt‖ ≤ L(wtvt),θt(i,j)=1 andθt(i,j)=0 otherwise.According to [13],the delaybetweenwtandvtcan be calculated as:

wherecdenotes the speed of light.

Migration model:The SFC migration procedure is triggered in the beginning of the time slots when new SFCs arrive.Migrating VNFs consumes bandwidth to transmit state data to new destinations,which is simplified or ignored in some ground networks due to the sufficient resources.However,in satellite networks,the bandwidth is limited.Therefore,to save link resources,the migration cost should include the bandwidth cost,defined as

2.3 Problem Formulation

For VNFfu,i,t,it can be placed on only one satellite,i.e.,

The constraints to be met for migration:Assume that the schemes of SFCs inwere already determined at time slot (t-1) by following the placement constraints above.The new placement procedure reschedules all SFCs (includingfor the best of the current momentt,which may induce the migration of SFCs inexpressed as

Denote binary variableto indicate whether link (w,v) is used to connect the migration destination offu,i,tto its original location.To guarantee successful migration,there should be an available path to transform data from the original node to the migration destination,i.e.,

The constraints of bandwidth,CPU and E2E delay:For each satellite noden ∈Nsat,all VNFs allocated to it should not exceed its CPU and memory capacities,i.e.,

whereandare the used CPU and memory resources beforet-1 (includingt-1),respectively.For each link inGt(V,E),the total bandwidth consumed by all SFCRs passing through it should not exceed its capacity,i.e.,

whereis the used bandwidth before and includingt-1.At last,each SFCushould satisfy the E2E delay requirement.The delay ofucontains the processing delay of VNFs and the propagation delay from its source to its destination.Therefore,we have:

wheredm,nis the propagation delay of link (m,n),anddenotes the processing delay of VNFi.

The objective function:With all the constraints defined above,we can formulate the online SFC placement and migration problem.We aim to reschedule all the arrived SFCs to maximize the total profit,defined as the rent of bandwidth and CPU resources of successfully placed SFCs minus the cost of migrating SFCs:

III.PROPOSED ALGORITHM

Since the SFC migration problem is NP-hard and could not be solved optimally within polynomial time,in this section,we aim to develop a heuristic algorithm,i.e.,MDSM,to solve the problem in a lower computational complexity.Besides,we also briefly show how to solve the problem with the BB algorithm.Finally,the complexity of MDSM and BB is compared.

3.1 The Minimized Dynamic SFC Migration Algorithm

Although BB can gain near-optimal solutions,the decision space may produce a significant computation overhead.Therefore,to reduce computational complexity,we propose the MDSM algorithm,a multistage heuristic algorithm that migrates SFCs only when they meet the migration trigger condition,to reach a trade-off between the migration frequency and the acceptance ratio of SFCs.As shown in Algorithm 1,in line 1-line 5,we determine when to migrate.After the migration procedure is triggered,the SFCs to migrate are determined in line 6-line 8 according to the overloaded nodes and links.In line 9-line 29,the migration destination is determined based on the minimum bandwidth cost criterion.The details of Algorithm 1 are introduced as follows.

When to migrate: Since remapping every SFC in each time slot may cause unnecessary migration and larger bandwidth cost,to avoid that,we restrict the migration procedure to begin only if a new SFC is rejected.Specifically,when a new time slottbegins,MDSM adopts the Viterbi algorithm[16]to place newly arrived SFCs.For simplicity,we reserveppossible paths for each SFC to place andDstates for each stage when applying the Viterbi algorithm.If SFCuis rejected due to the shortage of resources or violation of its QoS requirements,MDSM will trigger the migration procedure,which includes selecting which SFCs to move and where to place them,to spare resources foru.

Which ones to migrate: Unlike existing works that migrate VNFs one by one,we migrate an entire SFC to a new path at a time,which could efficiently guarantee the ordering requirement of SFC.The SFCs to be migrated are those occupying pathpi(denoted asSo(pi)),wherepi ∈pis a path that could meet the E2E delay ofubut is now overloaded,andpdenotes the set of potential paths used in Viterbi.Moreover,we consider that SFCu1occupiespi ∈pif any of its VNFs is located on any node alongpi.Different paths inpmay result in different SFCs being migrated and various migration schemes.To find the schemes that minimize the bandwidth cost,MDSM first sorts all paths inpbased on the number of hops in ascending orders.The fewer hops a path owns,the less bandwidth cost it may bring.Then for the first pathpj ∈p,So(pi)is acquired first and migrated one by one to new paths.The way to determine these destination paths will be discussed later.Once an SFCum ∈So(pi)is successfully migrated,MDSM uses theUpdate()function to replaces(um) with the migrated schemes′(um) ins(Ut) to gets′(Ut).Then MDSM remaps the rejecteduagain and checks if it is accepted.If that is the case,MDSM sets the flag of successful placementflag(ut) to 1,stops migrating SFCs inSo(pi),and continues to place another new SFC att(line 2).Otherwise,MDSM keeps conducting line 8-line 23 to migrate SFCs inSo(pi) untiluis accepted.Ifustill is not accepted after the procedure of line 8-line 23,MDSM repeats line 6-line 27 with another path inp(ut).After all paths inp(ut)are searched,ifustill is not accepted,the migration fails.

3.2 Complexity Comparison

The computational complexity of MDSM isO(|U1|2D|p||V|F),where|U1| is the number of successfully placed SFCs andFis the maximum VNF number for an SFC.

As the formulated problem is an ILP problem,it can be solved via the BB algorithm.We solve the problem with the ready-made solver Cplex to find the solutions.The complexity of it can be calculated asO(|V||Lsat||U|T||2|I||T|),where|U|T||is the number of all arrived SFCs.Obviously,the complexity of the BB algorithm is related to the number of arrived SFCs and the simulation time.If the simulation time is long,and the total number of SFCs is high,it will take plenty of time for the BB algorithm to find the solution.For MDSM,its complexity does not grow with time.With proper choices of the parameters of the Viterbi algorithm,the computational complexity will be lower than that of the BB algorithm.If the network operators require quick solutions and need to save computing resources,adopting MDSM is more reasonable.

IV.SIMULATION RESULTS

In this section,we provide simulation results to evaluate the performance of the proposed MDSM algorithm.

4.1 Simulation Setup

We use system tool kit(STK)to generate the satellite topology with 12 Iridium satellites.Each satellite is equipped with 96 CPU cores and 112 GB memory[3].The bandwidth of ISLs is 100Mbps.To make the service arrival procedure more realistic,we let the arrival time of SFCR follow a Poisson process.Each of the SFCRs stays in the system for 6 time slots and then leaves the system.The length of each SFC is randomly generated from [2,5],with each length representing one type of service.The bandwidth it requires is[3,10]Mbps,and the E2E delay requirement is uniformly distributed between 60 ms to 120 ms.The CPU and memory requirements of each VNF are[2,4]cores and[4,8]GB.The processing delay of each VNF is set as[5,10]ms.The main parameters of the simulations are summarized in Table 1.

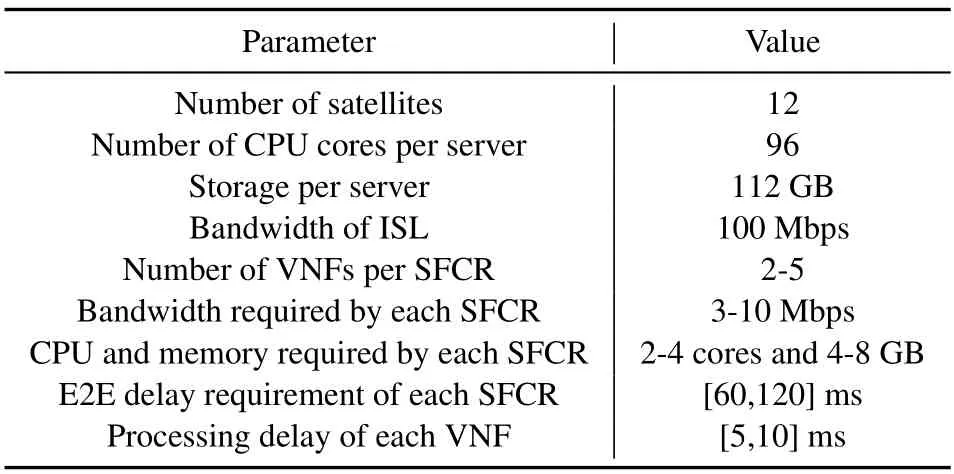
Table 1.Simulation parameters.

To verify the effectiveness of MDSM,as shown in Figure 2,we first evaluate the influences of the weight factorβon the performance of MDSM in terms of bandwidth cost,migration cost,and total profit.We consider a small satellite network including 6 SDN/NFV-enabled satellites,which indicates that SFCs can only be placed in 6 out of 12 satellites.The service arrival rateλis set as 8.βis varied from 2 to 7 with a step of 1 forT=2,4,6,8,10 while keeping other parameters unchanged (α=40,γ=0.4 [17]and the total number of arrived SFCs) and get the bandwidth cost for MDSM.

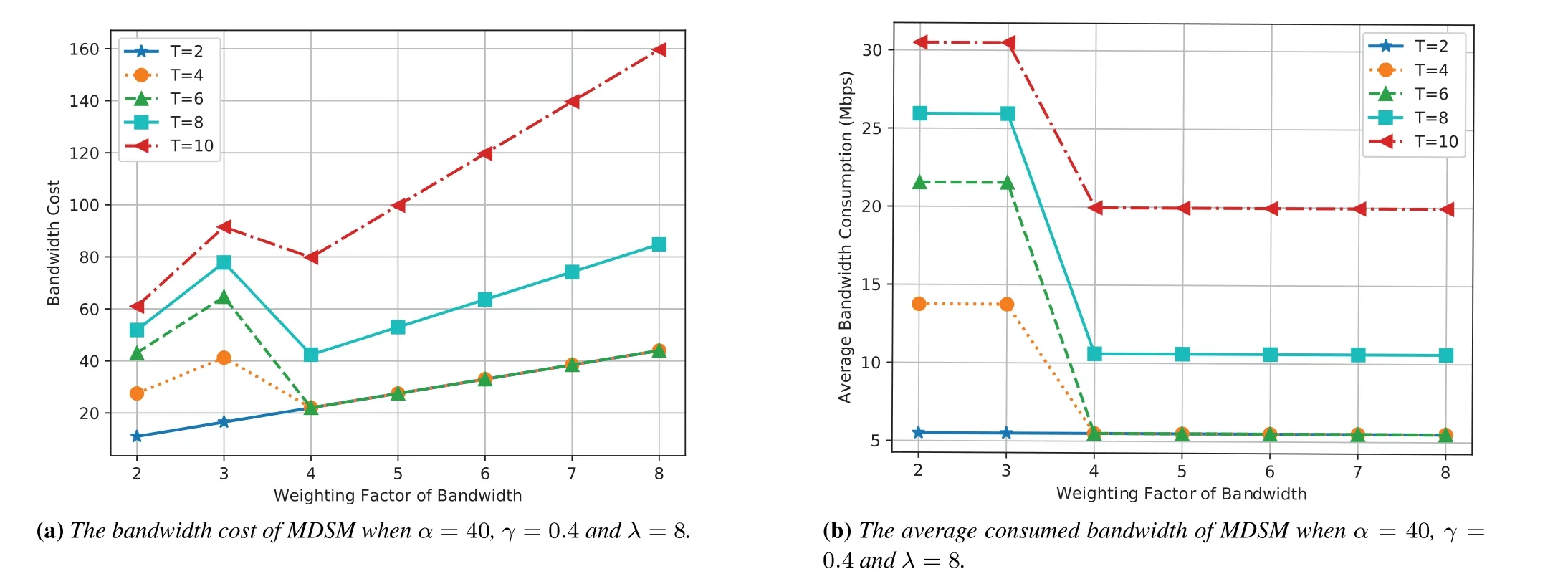
Figure 2.Bandwidth consumption and cost of MDSM.

In detail,Figure 2a shows the relationship betweenβand the bandwidth cost.It can be observed that the bandwidth cost of all time slots has an ascending trend with the growth ofβ.This is predictable due to the definition of bandwidth cost,known as the product ofβand the actual average bandwidth consumption of all accepted SFCsThe value of the bandwidth consumption can reflect the number of accepted SFCs.The more SFCs are accepted,the higher the bandwidth consumption is.For a given value of bandwidth consumption,the biggerβis,the higher the product ofβandis.Besides,there are two phenomena worth noticing.First,whenβvaries from 2 to 4,the bandwidth cost ofT=4,6,8,10 increases first and then decreases.Second,the bandwidth cost ofT=2,4,6 is the same whenβlies between 4 and 8.

The above mentioned phenomena can be explained by Figure 2b,which depicts the average bandwidth consumption under differentβ.It can be seen that the bandwidth consumption ofT=4,6,8,10 decreases from 3 to 4,leading to the reduction of the bandwidth cost.In other words,whenβgrows from 3 to 4,the number of accepted SFCs is fewer.The reason is that if the weighting of bandwidth cost is high,it engages an SFC with many hops costs too much.Under this situation,the migration frequency will be reduced,as the migration procedure may yield lower profits from accepting new SFCs than the migration and bandwidth cost.Furthermore,due to the resource shortage caused by pre-occupation and less migration,new SFCs are more likely to be rejected to balance the high bandwidth cost.In addition,the bandwidth consumption ofT=2,4,6 is the same as the value ofβvaries from 4 to 8,which leads to the second phenomenon mentioned above.It is because the high value ofβstops the acceptance of newly arrived SFCs,until node resources are released for them due to the leave of the existing SFCs.In a word,the value ofβcan influence the bandwidth consumption.Within a reasonable range,it can help the system to accept more SFCs by bringing up the migration frequency.However,when the value is too big,it can stop more SFCs from acceptance.It is wise to chooseβaccording to the network operators’needs.

4.2 Performance Evaluation of MDSM

To evaluate the influences ofβon the migration cost,we calculate the migration cost under different values ofβ,as shown in Figure 3.Whenβgrows,the migration cost initially increases,then decreases,and eventually reaches 0.As mentioned above,from 2 to 3,when the bandwidth consumption starts to weigh more,the migration is triggered more frequently to spare node resources for newly arrived SFCs.However,ifβis bigger,the migration schemes that raise the total profits brought by all SFCs are fewer.Thus,the migration cost ofβ=4 is fewer than that ofβ=3.Whenβcontinues increasing,there are no migration schemes to guarantee a rather low bandwidth cost for existing SFCs,resulting in no migration at all.

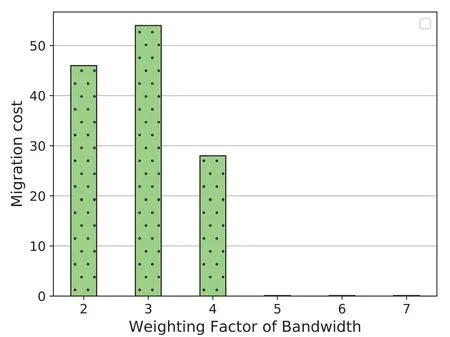
Figure 3.The migration cost of MDSM.

At last,we report the total profits of MDSM under different values ofβin Figure 4.Obviously,the total profit ofβ=2 is the highest among all curves.According to Equation.(13),the value of total profit is decided mainly by the number of accepted SFCs and the bandwidth cost.Whenβ=2,the bandwidth cost weights the least,which motivates rather frequent migration to accept more new SFCs and raises the profits of the accepted SFCs,named the placement profit.With the highest placement profits and low bandwidth cost,the curve ofβ=2 stands above all the other curves.The curve ofβ=3 is very close to that ofβ=2.It is because the migration is still triggered frequently to spare resources for new SFCs.The successfully placed new SFCs increase the placement profits ofβ=3,causing the total profit closer to that ofβ=2.Notably,after the slow growth from 4 to 5,the total profits ofβ=2,3 grows faster.The reason is that node and link resources are released atT=7 due to the departure of some placed SFCs.New SFCs can be accepted because of these spared resources.For curves ofβ=4,5,6,7,their total profits are smaller than those ofβ=2,3,since their numbers of accepted SFCs are smaller.In addition,their total profits stop growing from 2 to 7 and begin increasing atT=7,the exact time when resources occupied by arrived SFCs are released.

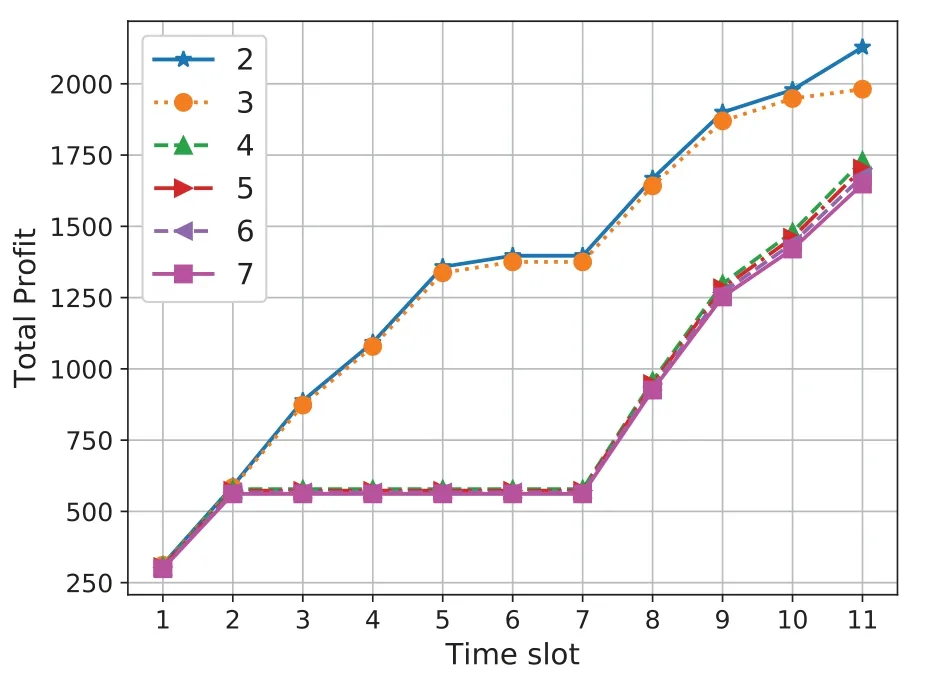
Figure 4.The total profits of MDSM under different β.

According to the above results,the conclusion can be drawn that our MDSM can adjust the migration frequency to accommodate more SFCs and create higher total profits when the bandwidth resources are not too tight.If bandwidth resources are scarce,MDSM chooses to avoid migration and placement of new SFCs until some existing SFCs leave the system.

4.3 Performance Comparison

To verify the effectiveness of MDSM when the satellite topology is dynamic,the experiments are conducted under two cases,namely Case I and Case II.In Case I,only the service requirements are arrived dynamically,following Poisson process.In Case II,not only do the services arrive dynamically but also the satellite topology changes with time.Further,we compare the performance of MDSM to other benchmark algorithms,namely BB,MSH-OR [10] and no migration-based Viterbi(NM-VIT).

BB: The results of BB are obtained by solving the model with Cplex solver.In this paper,we regard the performance of BB as the upper bound of the ILP problem.

MSH-OR:MSH-OR triggers migration based on the empirical CPU utilization threshold of the node.To minimize the E2E delay of SFCs,it chooses nodes close to the original nodes where VNFs stay as the migration destinations.

NM-VIT: NM-VIT does not consider migrating VNFs.It utilizes the Viterbi algorithm[16] to place SFCs to minimize the bandwidth cost.If there are not enough resources for a newly arrived SFC,it will be directly rejected with no adjustment.

Figure 5a and Figure 5b portray the acceptance ratio of SFCs in Case I and Case II,respectively.It can be observed that in both cases the acceptance ratios of all algorithms initially decrease over time,and then they start to grow.The reason is that from time slot 1 to time slot 6,the network resources steadily drain out,which makes it hard to accept new SFCs.The number of total accepted SFCs,defined asNacc,stops increasing,while the number of all arrived SFCs,known asNtotal,keeps rising.According to the definition of acceptance ratio,known as,the value of acceptance ratio decreases.However,placed SFCs start to leave the network atT=7,sparing more node and bandwidth resources for new SFCs.Thus,more new SFCs arriving afterT=6 can be placed,which raises the value of the acceptance ratio.

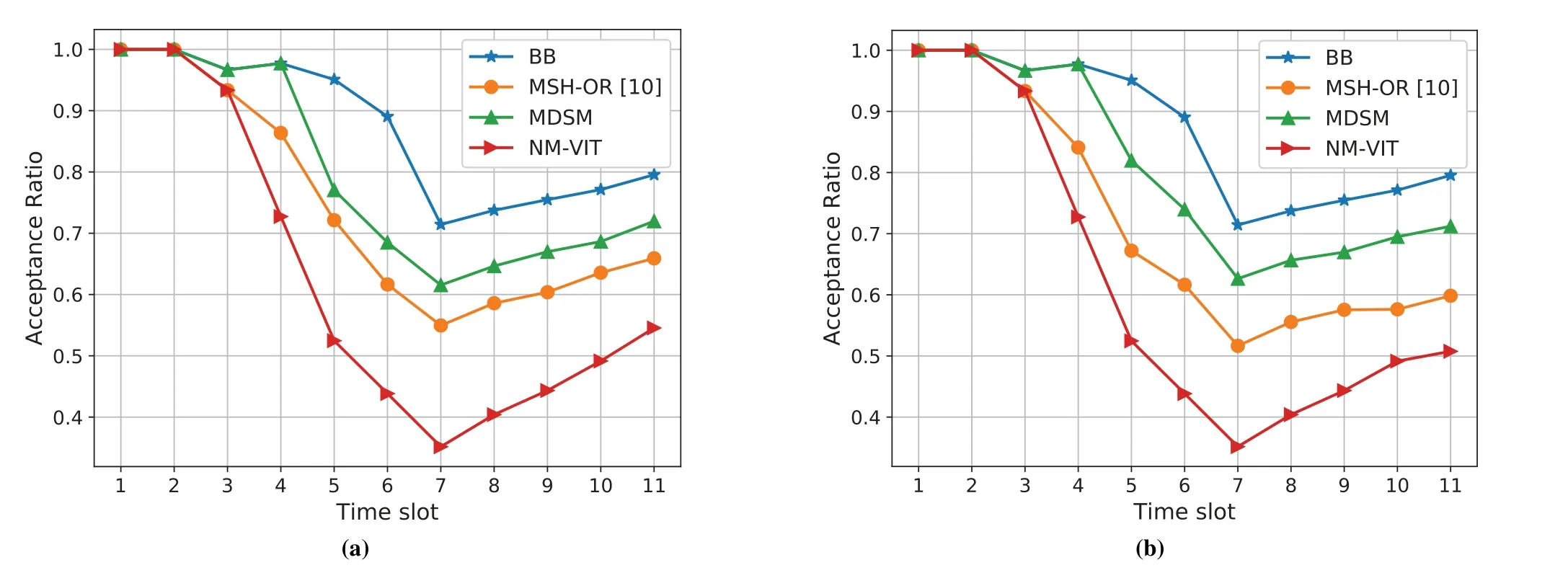
Figure 5.Acceptance ratio in two cases. (a)Case I.(b)Case II.

Among all algorithms,BB raises the acceptance ratio by 16.6% and 26.2% compared to MSH-OR and NM-VIT in Case I and 14.2% and 26.2% in Case II,while MDSM raises the ratio by 12.6% and 22.2%in Case I and 9.9% and 21.9% in Case II.In both cases,BB and MDSM admit more SFCs than the other benchmark algorithms.The reason is that BB attempts to get the global optimum by remapping all arrived SFCs in each time slot,which gives BB enough information to get better migration solutions than other benchmark algorithms.MDSM only starts migration when a new SFC is rejected and reschedules a limited number of SFCs that consume the resources required by the new SFC.Although it admits fewer SFCs than BB due to its smaller scope of rescheduling,it still outweighs MSH-OR and NM-VIT.MSH-OR triggers migration merely based on an empirical utilization threshold and determines the migration destination without considering the bandwidth,which may cause unnecessary migration,waste link resources and further lead to a low acceptance ratio.NM-VIT is a static algorithm that could not move VNFs according to the real-time QoSs,causing the lowest acceptance ratio.

Notably,the average ratio of BB in Case II is basically the same as that in I,concluding that BB can guarantee the acceptance ratio when the satellites move dynamically.For MDSM,the ratios att=5,6 in Case I are smaller than those in Case II.When the network topology changes,some migration schemes with less migration cost and hops might show up compared to the static topology.Since MDSM makes migration and placement decisions based on the new global topology,it can find the near-optimal migration and placement schemes to increase the acceptance ratio.In contrast,with the same time interval,the acceptance ratio of MSH-OR is smaller in Case II.It is because MSH-OR only determines migration schemes based on the local topology near the overload satellites.It is more likely for MSH-OR to find highcost migration schemes or even no migration schemes,causing the failure of new SFCs.What’s more,MSHOR does not trigger the migration when a new SFC is rejected.This reduces the possibility of the rejected SFC being accepted again.

In a word,the proposed MDSM can deal with the dynamic of satellites by utilizing enough network topology information,while keeping less frequent migration.

Similar conclusions can be drawn in terms of the total profit in Figure 6a and Figure 6b,which demonstrate the total profit of four algorithms in two cases.In both cases,the curves of four algorithms have an ascending trend.The total profits of the four algorithms are close in the beginning,while at the end,BB and MDSM have higher total profits than MSH-OR and NM-VIT.On average,BB is 61.9% higher than NMVIT in Case I and 62.3%higher in Case II,and MDSM promotes the total profit by 51.2%in Case I and 50.8%in Case II compared to NM-VIT.Notably,the curves of BB stop increasing from 6 to 7 in both cases,and keep growing afterT=7.The reason is that from 6 to 7 the resources are run out.No more new SFCs arrived atT=6 can be accepted,leading to no growth of the total profits.In addition,BB promotes 0.4%more profits against the static algorithm in Case II compared to Case I,which shows the adaptability of BB to the dynamics.For MDSM,the curves of both cases keep growing,even from 6 to 7.It suggests that MDSM does not reach the bottleneck before placed SFCs are released.MDSM promotes 0.4%fewer profits against the static algorithm in Case II compared to Case I,which is smaller than that of BB but higher than that of MSH-OR.

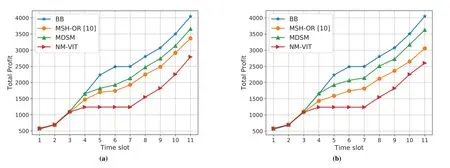
Figure 6.Total profits in two cases. (a)Case I.(b)Case II.

V.CONCLUSION

In this paper,we considered the dynamic topology and scarce bandwidth resources in the LEO satellite networks,we introduced migration when placing SFCs to guarantee the network system to accept as many SFCs as possible.An algorithm,namely MDSM,was proposed to balance the total profits and bandwidth cost.To avoid frequent migration and inappropriate migration schemes,we only migrated SFCs when a new SFC was rejected,chose SFCs with smaller migration costs to move,and migrated them to paths with fewer hops.Simulation results demonstrated that MDSM can ensure profits that are close to the upper bound provided by the BB algorithm.The proposed algorithm could be used as an inspiring resource scheduling framework for the dynamic LEO satellite networks to deploy services based on their interests.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China(NSFC)under grant numbers U22A2007 and 62171010,the Open project of Satellite Internet Key Laboratory in 2022 (Project 3:Research on Spaceborne Lightweight Core Network and Intelligent Collaboration),and the Beijing Natural Science Foundation under grant number L212003.