Low-Complexity Reconstruction of Covariance Matrix in Hybrid Uniform Circular Array

Fu Zihao ,Liu Yinsheng ,Duan Hongtao

1 Information School,Communication University of China,Beijing 100024,China

2 Beijing Institute of Electronic System Engineering,Beijing 100854,China

3 School of Electronic and Information Engineering,Beijing Jiaotong University,Beijing 100044,China

4 Beijing Radio Monitoring Station of State Radio Monitoring Center(SRMC),Beijing 100037,China

Abstract: Spatial covariance matrix (SCM) is essential in many multi-antenna systems such as massive multiple-input multiple-output (MIMO).For multi-antenna systems operating at millimeter-wave bands,hybrid analog-digital structure has been widely adopted to reduce the cost of radio frequency chains.In this situation,signals received at the antennas are unavailable to the digital receiver,and as a consequence,traditional sample average approach cannot be used for SCM reconstruction in hybrid multi-antenna systems.To address this issue,beam sweeping algorithm (BSA) which can reconstruct the SCM effectively for a hybrid uniform linear array,has been proposed in our previous works.However,direct extension of BSA to a hybrid uniform circular array(UCA)will result in a huge computational burden.To this end,a low-complexity approach is proposed in this paper.By exploiting the symmetry features of SCM for the UCA,the number of unknowns can be reduced significantly and thus the complexity of reconstruction can be saved accordingly.Furthermore,an insightful analysis is also presented in this paper,showing that the reduction of the number of unknowns can also improve the accuracy of the reconstructed SCM.Simulation results are also shown to demonstrate the proposed approach.

Keywords: hybrid array;millimeter-wave;spatial covariance matrix;uniform circular array

I.INTRODUCTION

Spatial covariance matrix (SCM) have been widely used in many multi-antenna systems,such as cellular communications,radars,and direction finding systems[1].For example,massive multiple-input multipleoutput(MIMO)is one of the most important enabling technologies in 5G[2].Due to a large number of antennas,massive MIMO is essential to millimeter-wave bands because large array gain can compensate for the high path loss and frequency resources at millimeterwave bands can be exploited efficiently [3,4].Different from cellular systems where uniform linear arrays (ULA) are widely adopted,uniform circular arrays(UCA)are more popular in direction finding systems.Omni-directional feature of UCA can deliver the same estimation accuracy regardless of the direction of receiving signals,and it has been thereforede factorreference in practical direction finding systems[5][6].

To reduce the cost caused by the radio frequency(RF) chains operating at millimeter-wave bands,hybrid analog-digital structure has been adopted in many multi-antenna systems [7-9].In hybrid massive MIMO,one RF chain is connected to multiple antennas,so that the number of RF chains can be much smaller than the number of antennas.In this case,however,received signals at the antennas are first fed to the analog devices and then combined before send to the digital receiver.Consequently,received signals at the antennas are unavailable to the digital receiver and thus traditional sample average approach cannot be used for SCM reconstruction [10].To address this issue,we have developed a beam sweeping algorithm (BSA) for SCM reconstruction in hybrid ULA[11,12].In this approach,beam sweeping results corresponding to a group of predetermined directionof-angles (DOA) are collected and then SCM can be reconstructed by solving a matrix equation.Predetermined DOAs are carefully selected in [13] so that matrix inverse can be completely avoided.A truncated BSA has also been proposed in[14]to accelerate the sweeping procedure.To reduce the complexity of solving matrix equation,analog switches are also considered in[15]to adjust the weights connected to each antenna.Furthermore,high computational complexity can be also addressed by adopting new computation platform,such as quantum computer[16].

In spite of the success of BSA in SCM reconstruction for hybrid ULA,discussion on BSA in the case of hybrid UCA is still absent.A straightforward way is to use the basic BSA in [11] directly for SCM reconstruction in hybrid UCA.Although simple,direct extension of basic BSA to the hybrid UCA case will result in a huge computational burden.Moreover,as the steering vector of UCA is essentially different from that of ULA,the predetermined DOAs selected in[13]cannot be used in hybrid UCA either.To this end,we propose a low-complexity approach for SCM reconstruction in hybrid UCA in this paper.By exploiting the symmetry features of SCM for the UCA,the number of unknowns in the desired SCM can be reduced significantly and thus the complexity of reconstruction can be saved accordingly.Furthermore,an insightful analysis will show that the reduction of the number of unknowns causes a low-dimensional diagonal loading,and as a result,the reconstruction accuracy can be improved compared to the full-dimensional diagonal loading in[11].

The rest of this paper is organized as follows.In Section II,signal model for hybrid UCA is introduced,followed by a review of SCM reconstruction issue.In Section III,basic BSA will be first reviewed in brief and then the low-dimensional reconstruction approach will be presented based on the symmetry feature of SCM.The performance analysis will be presented in in Section IV.Finally,simulation results and conclusions are in Section V and VI,respectively.

II.SYSTEM MODEL

2.1 Signal Model

As in Figure 1,consider a hybrid UCA system which is composed ofMantennas on a circle with radiusR.To simplify the symbol notation,a single RF chain is considered in this paper.Using the approach in [12],the proposed algorithm in this paper can be also applied in the case of multiple RF chains.

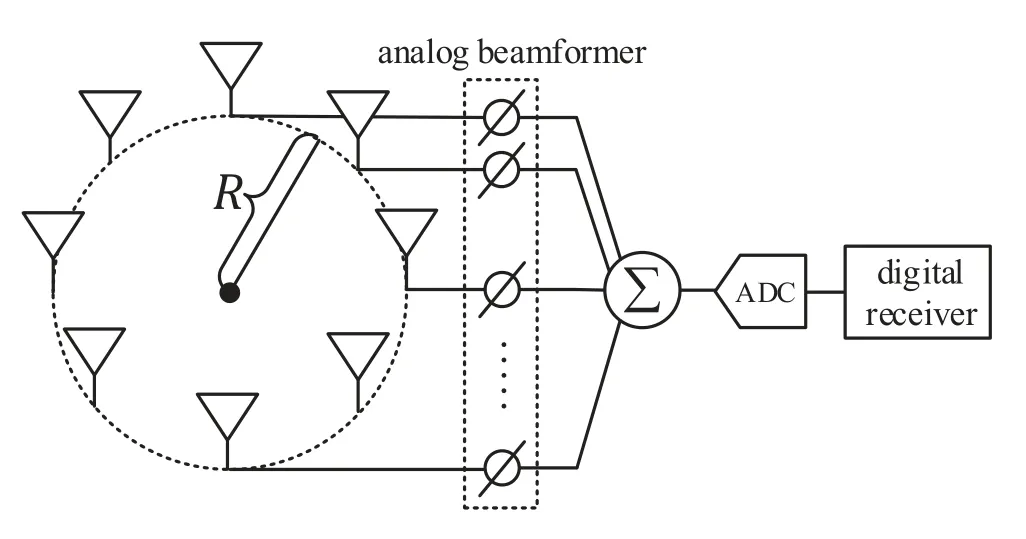
Figure 1.Hybrid UCA with a single RF chain. The number of antennas is M and the radius is R.

Denoteym(t)(m=0,1,···,M-1)to be the received signal on them-th antenna,then the received signal vectory(t)=[y0(t),y1(t),···,yM-1(t)]Tcan be represented as

wherexl(t)’s(l=0,1,···,L-1)areLsignals impinging from far field onto the array,θlis the DOA ofxl(t),andz(t)denotes the additive Gaussian noise vector with E{z(t)zH(t)}=N0IwithN0andIbeing the noise power and an identity matrix,respectively.In(1),a(θl)is theM×1 steering vector with them-th element given bywhereλindicates the wave length.

If assumingLsignals are mutually independent with zero means and the power of thel-th signal is E{|xl(t)|2}=then the SCM,R=E{y(t)yH(t)},can be obtained as

where the(m,n)-th element ofRcan be represetend,using(2),as

2.2 SCM Reconstruction

Denotey[n]=y(nT) to be then-th sample of received signal whereTdenotes the sampling period.If all elements ofy[n] are available to the digital receiver,SCM in(3)can be approximated using the sample average approach as[17]

whereNdenotes the number of samples.In this approach,received signals at all antennas should be sent via RF chains to the digital receiver.In hybrid arrays,however,Figure 1 shows that only the combination of the elements ofy[n]can be seen by the digital receiver because there is only one RF chain.As a consequence,the sample average approach in(5)cannot be used in hybrid arrays.To address this issue,BSA and its improvement have been proposed for SCM reconstruction in hybrid ULA in our previous works[11,13,12].It has shown that BSA can reconstruct the SCM effectively and efficiently in the case of hybrid ULA.

In spite of the success of BSA in SCM reconstruction for hybrid ULA,discussion on BSA in the case of hybrid UCA is still absent.In the subsequence of this paper,we will focus on the SCM reconstruction issue in hybrid UCA.

III.LOW-COMPLEXITY RECONSTRUCTION

In this section,the basic BSA will be first reviewed as a baseline.Then,the low-dimensional reconstruction algorithm will be shown by exploiting the symmetry feature of SCM.

3.1 Review of Basic BSA

As in[11],define{θ(0),θ(1),···,θ(Q-1)}to be a set of predetermined DOAs.Different from the case of ULA where-π/2＜θ(q) ＜π/2,we have-π ＜θ(q) ＜πin the case of UCA.Then,the analog beamformers switch the beam directions to the predetermined DOAs in turn.For theq-th beam,the combination of the received signals can be represented by

From Figure 1,the signal combination is sampled before sent to the receiver,and thus the samples of the signal combination can be given by

DenotePq=E(|cq[n]|2) to be the average power ofcq[n],when the number of samples is large enough,we have

Using vec(·)operator to(8),Pqcan be rewritten as

wherer=vec(R)andaq=a(θ(q))⊗a*(θ(q))with⊗indicating Kronecker product.If taking allQpredetermined DOAs into account,we can derive that

wherep=(P0,P1,···,PQ-1)Tcontains the estimated power on all predetermined beams andA=(a0,a1,···,aQ-1)T.As in [11],unknownrcan be obtained by solving(10)as

whereσ2is a diagonal loading coefficient to avoid illconditioned solution.Then,the desired SCM can be reconstructed as=unvec

The computational complexity of basic BSA main results from the matrix inverse in (11).As there areM2unknowns in,matrix inverse has to be conducted with respect to anM2×M2matrix,causing a huge computational burden.

3.2 Low-Dimensional Reconstruction Algorithm

3.2.1 Symmetry Feature of SCM

AlthoughrcontainsM2elements,many elements inrare actually the same.Therefore,an efficient way to reduce the computational complexity is keeping only the elements that are different to each other while removing the same and repeated elements contained inr.This can be achieved by exploiting the symmetry features of SCM.

In particular,if denote[R]m,nto be the element on them-th row and then-th column ofR,then we can derive,from(4),that

for 0≤m,n ＜M/2,and

for 0≤m ＜M.Using(12)to(15),the desired SCMRcan be rewritten as

wherea0(θ(q)) anda1(θ(q)) contain the first and the lastM/2 elements ofa(θ(q)),respectively,anda1(θ(q))=(θ(q)).

3.2.2 Low-Dimensional Reconstruction

Substituting (16) to (19) into (8),the beam sweeping result in(8)can be rewritten by

where we have used the identity

Substituting(17)and(18)into(20),we have

where we have used the identities

Then,if using vec(·)operator to both sides of(22),

To rewrite (25) in a vector form,denoteγto be a column vector that contains all+1 non-repeated unknowns andb(θ(q))to be a column vector that contains the coefficients corresponding to all non-repeated unknowns,that is

With(26),(25)can be rewritten in vector form as

Note that(27)considers only one predetermined DOA,if allQpredetermined DOAs are taken into account,we have

whereB=[b(θ(0)),b(θ(1)),···,b(θ(Q-1))]T.Then,theM2/2+1 non-repeated unknowns contained inγcan be obtained by solving(28)as

whereσ2is a diagonal loading coefficient used to avoid ill-conditioned result.Onceγis obtained,the desired SCM can be reconstructed using the nonrepeated elements inγ.

Similar to (11),the computational complexity mainly results from the matrix inverse in (29).However,as the number of unknowns is reduced fromM2toM2/2+1,matrix inverse is now conducted with respect to an(M2/2+1)×(M2/2+1)matrix.Therefore,compared to (11),the reduction of the number of unknowns has lead to a significant reduction in the computational complexity.

IV.INSIGHTS

In this section,we will first discuss the ranks of matricesAandB,then a performance analysis will be shown.

4.1 Analysis of Ranks

with 0≤m,n ＜M/2,and

Therefore,we conclude that ifthen(θl)an1(θl)=(θl)an2(θl).In other words,the coefficients associated with the repeated unknowns inRare also the same.The above conclusion can be also applied ifQpredetermined DOAs are taken into account,that is,the columns ofAare the same if they corresponds to the repeated unknowns inr.In particular,if denoteA=[α1,α2,···,αM2]whereαiis aQ×1 vector,then we can obtain thatαi=αjif thei-th and thej-th elements ofrare the same.

On the other hand,it shows in (27) that the elements inb(θ(q)) corresponds to non-repeated unknowns inr,and therefore the elements inb(θ(q))are not necessarily the same.Accordingly,if denoteB=[β1,β2,···whereβiis aQ×1 vector,thenβiandβjare also not necessarily the same for.In fact,Bcan be obtained by combing the repeated columns inA,as illustrated in Figure 2.Figure 2 shows that the repeated columns inAhave been combined while only the non-repeated columns are kept inB.Since combing the repeated columns has no impact on the column space spanned byA,we can therefore obtain that

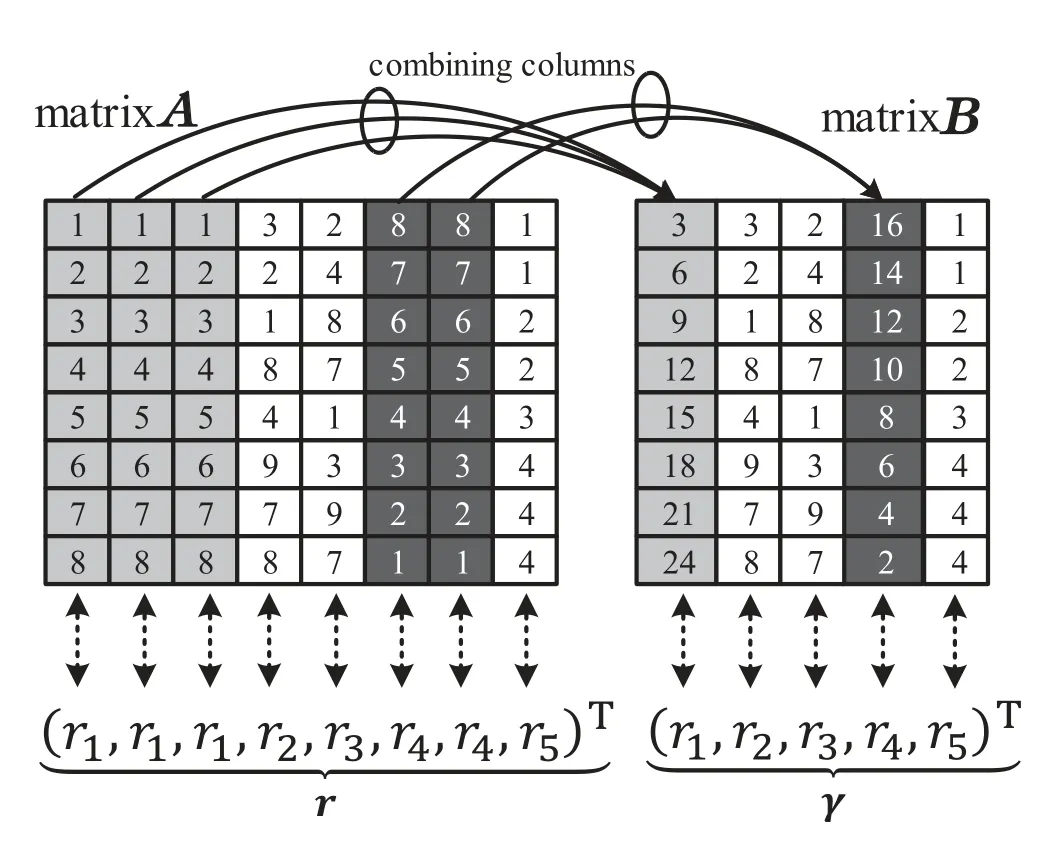
Figure 2.An example of relations between matrices A and B and corresponding unknowns in r and γ.

4.2 Performance Analysis

In[14],the squared-error(SE),‖R-has been used to evaluate the performance of BSA in the case of ULA.However,the geometry of UCA makes it difficult to derive a closed-form expression of SE.Even though,a rough performance analysis can be still derived using the fact that rank(A)=rank(B)=K.

As there areM2/2+1 non-repeated unknowns in total,the SE can be rewritten,in terms of the nonrepeated unkowns,by

Comparing to (41),additional error components are included into the upper bound in(36).As a result,the upper bound may get loose ifMis very large because more errors components are included.However,it can be very tight whenMis small because few error components are included into the upper bound.

whereΛ=I-(Δ+σ2I)-1Δ.Since rank(B)=K,we havedm=0 whenm ＞K.Furthermore,to derive insightful results,a diaognal loading coefficient that is sufficiently small can be employed so thatdm ≫σ2whenm ≤K.In this case,the (m,m)-th diagonal element ofΛcan be approximated as

Therefore,‖γ-can be rewritten as

Intuitively,as there areM2/2+1 non-repeated unknowns inγ,matrixBshould haveM2/2+1 independent columns so as to derive a unique solution for(28)and thereforeKshould be aroundM2/2+1 whenQis large enough.This intuition has been verified by the numerical results in Section IV.It shows thatK+1 can be as large asK+1≈+1 whenQis large enough.In this case,the approximation in(39)can be further simplified as

Substituting(40)into(36),the upper bound in(36)can be rewritten by

That is,the upper bound is composed of aboutMidentical error components.

Similarly,if using the basic BSA directly,‖R-can be given by

Since rank(A)=rank(B)=K,following a similar procedure as from(37)to(39),the SE in(42)can be rewritten as

V.SIMULATION RESULTS

In the simulation,we consider a hybrid UCA where the radius isR=Mλ/4πso that the distance between neighboring antennas is aboutλ/2.Two signals with unit power are impinging onto the UCA fromθ=180oand 300o,respectively.Qpredetermined DOAs are uniformly distributed from 0oto 360o,and different values ofQwill be considered in the simulation.

Figure 3 shows the ranks ofAandBin the cases of different numbers of antennas.As expected in the analysis,AandBhave the same ranks.WhenQis small,the ranks of both matrices increase as the rising ofQ.WhenQis large enough,the ranks cannot increase further as the rising ofQand is fixed at aboutM2/2.This observation can be used to justify the performance analysis in Section IV.

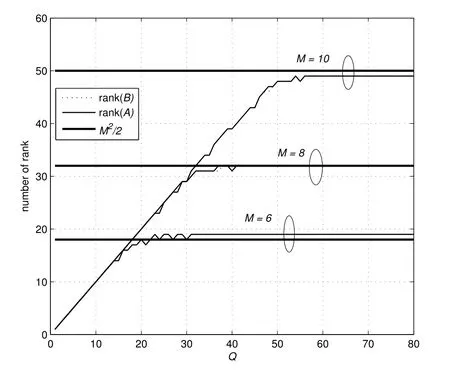
Figure 3.Ranks of A and B with different number of antennas.

Figure 4 shows the reconstruction accuracy in terms of normalized SE,NSE=‖R-·‖R‖Direct application of the approach in [11] for hybrid UCA is considered in this figure as a baseline.As shown in this figure,whenQis large enough,the low-complexity approach proposed in this paper can achieve better performance than using the approach in [11] directly.This observation coincides with our performance analysis in Section IV.It also shows in Figure 4 that the reducing the diagonal loading coefficient can improve the reconstruction accuracy of the proposed approach,while it has little impact on the directly applied approach in [11].The derived upper bounds have also been shown in this figure for comparson.

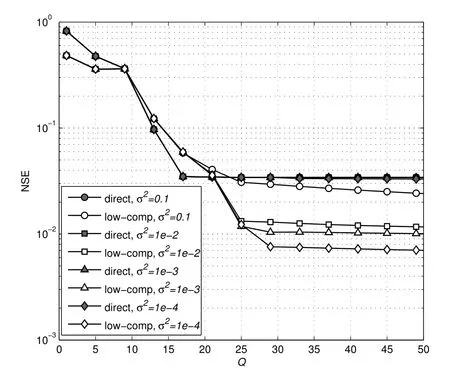
Figure 4.NSE performances of different algorithms where the SNR is-5 dB and the number of antennas is M=8.

Figure 5 compares the computational complexity of different approaches.Matrix inverion required in(11) and (29) are conducted on a computer with Intel(R)Core(TM)i7 processor running at 2.6GHz.Figure 5 shows the average time durations of different approachs to complete one matrix inversion operation.It shows clearly that the low-complexity reconstrution algorithm proposed in this paper can outperform the basic BSA significantly.

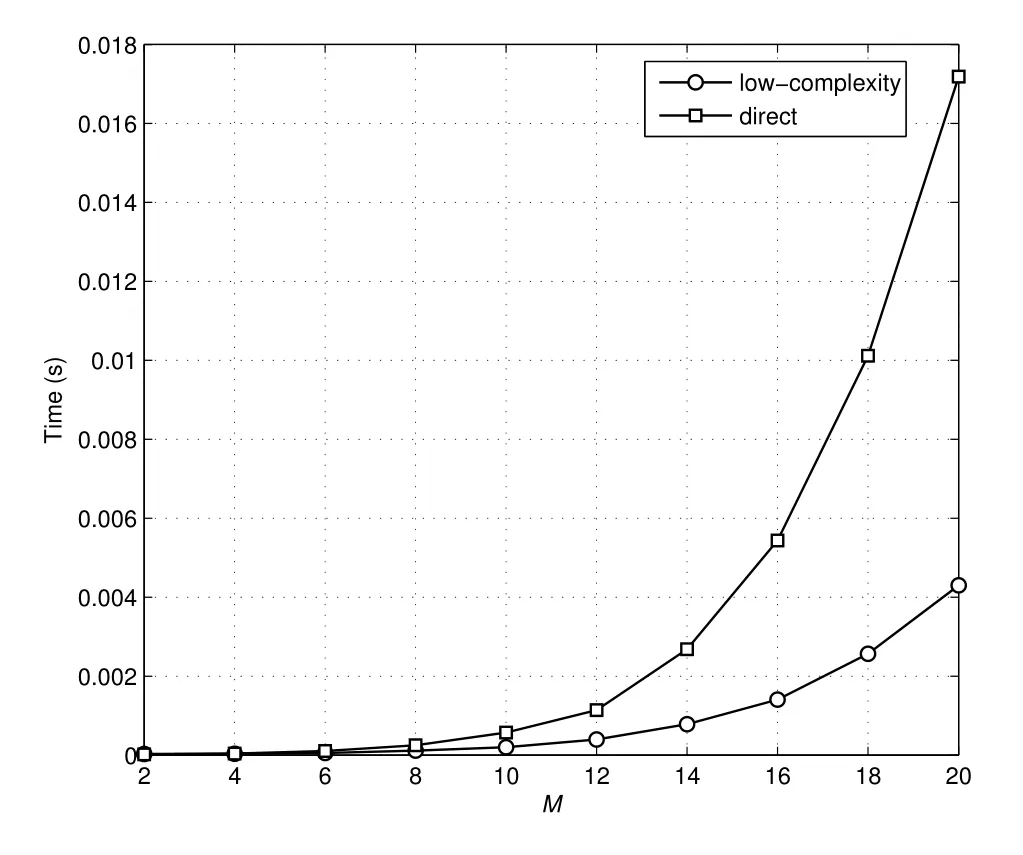
Figure 5.Comparison of computational complexity.

VI.CONCLUSION

In this paper,a low-complexity BSA has been proposed for SCM reconstruction in hybrid UCA.By exploiting the symmetry features of SCM for a UCA,the number of unknowns in the desired SCM can be reduced significantly and thus the complexity of reconstruction can be saved accordingly.Furthermore,insightful analysis have also shown that,in addition to the reduction of the computational complexity,the reconstruction accuracy can be also improved due to the reduction of the number of unknowns.Simulation results have also been presented in this paper to demonstrate the proposed approach.

ACKNOWLEDGEMENT

This work was supported by National Key Research and Development Program of China under Grant 2020YFB1804901,State Key Laboratory of Rail Traffic Control and Safety (Contract: No.RCS2022ZT 015),Special Key Project of Technological Innovation and Application Development of Chongqing Science and Technology Bureau(cstc2019jscx-fxydX0053).