Channel Estimation for Reconfigurable Intelligent Surface Aided Multiuser Millimeter-Wave/THz Systems

Chu Hongyun,Pan Xue,Li Baijiang

School of Communications and Information Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China

Abstract: It is assumed that reconfigurable intelligent surface (RIS) is a key technology to enable the potential of mmWave communications.The passivity of the RIS makes channel estimation difficult because the channel can only be measured at the transceiver and not at the RIS.In this paper,we propose a novel separate channel estimator via exploiting the cascaded sparsity in the continuously valued angular domain of the cascaded channel for the RIS-enabled millimeter-wave/Tera-Hz systems,i.e.,the two-stage estimation method where the cascaded channel is separated into the base station(BS)-RIS and the RIS-user(UE) ones.Specifically,we first reveal the cascaded sparsity,i.e.,the sparsity exists in the hybrid angular domains of BS-RIS and the RIS-UEs separated channels,to construct the specific sparsity structure for RIS enabled multi-user systems.Then,we formulate the channel estimation problem using atomic norm minimization (ANM) to enhance the proposed sparsity structure in the continuous angular domains,where a low-complexity channel estimator via Alternating Direction Method of Multipliers (ADMM) is proposed.Simulation findings demonstrate that the proposed channel estimator outperforms the current state-of-the-arts in terms of performance.

Keywords: atomic norm minimization;cascaded channel estimation;convex optimization;mmWave/THz;reconfigurable intelligent surface(RIS);sparsity

I.INTRODUCTION

The millimeter wave (mmWave) bands have a significant amount of untapped spectrum.Both at the transmitters and receivers,massive antenna arrays are required to make up for the substantial free space route loss [1-3].Compared to conventional sub-6 GHz multiple-input multiple-output(MIMO)systems with fewer broadcast and receive antennas,this makes channel estimation(CE)more challenging.Due to the small number of identifiable pathways in the angular domain,the mmWave MIMO channel is intrinsically sparse.As a result,methods for compressive sensing (CS) that make use of sparsity have been widely used to estimate the channel(parameter)of mmWave MIMO channels,such as in[4,5].

The idea of a reconfigurable intelligent surface(RIS) has recently been presented to intelligently change the propagation of electromagnetic waves in order to further increase spectrum efficiency(SE)and to provide a broad communication coverage[6-8].In comparison to a system without RISs,the RIS also has a tremendous potential to provide greater positioning and localization accuracy,both indoors and outdoors[8,9].By adjusting the phase of each RIS component,the array of phase shifters in the RIS may passively direct the beams toward the designated user(s).In[10],the authors study the use of reconfigurable intelligent terrestrial (RIS) for multi-antenna base station downstream multi-user communication.Under the premise of ensuring the link budget of mobile users,it is designed to save energy for the transmission power distribution and the phase shift of the surface reflective elements.Additionally,the results demonstrate that the suggested RIS-based resource allocation technique can offer up to 300%more energy efficiency than the multi-antenna amplified forwarding relay that is currently in use.

Recent research on CE for RIS-aided MIMO systems may be found in[11-14].In[11],the RIS channel estimation problem is effectively addressed using the methods of compressed sensing and deep learning.In[12],iterative CE is carried out by sequentially utilizing sparse matrix factorization and matrix completion.Due to the on/off state that is applied to the RIS pieces in this work,full utilization of the RIS is not possible.The phase control matrix at the RIS and the combining vector at the mobile stations (MS)was simultaneously designed using a multi-level codebookbased technique as opposed to predicting the MIMO channels[15].In[13,14],an extension to a multiuser situation was investigated.In[16],the author concentrates on the wireless communication system with RIS assistance and offers two combined channel estimation and signal recovery strategies based on message passing algorithms.In[17],this paper focuses on the multi-user multiple-input single-output(MISO)uplink communication system and provides a channel estimation method based on parallel factorization to expand the obtained cascaded channel model.For the channel between the base station and RIS and the channel between RIS and the user,we provide two iterative estimation strategies.One takes vector approximation messaging to iteratively recreate two unknown channels from the estimated vector,while the other is based on alternate least squares(ALS).

In this paper,we examine the mmWave/THz MIMO system’s CE issue using RIS assistance.The CE issue is split into two stages.Due to the fact of coupling,joint estimating two channels is difficult,but estimating partial information,e.g.,angle of arrival(AOA),is possible.The first stage is to formulate the AOA estimating problem as a semidefinite programming (SDP) via ANM,but the traditional methods,SDP-based methods are used to solve the ANM problem,which has high computational complexity and cannot be realized efficiently.Hence,we proposed a RIS-alternating direction method of multipliers(ADMM)algorithm to solve the above issues,and further calculate the RIS-to-BS channel based on the path-loss model and the locating information of the BS and the RIS.The second stage is estimating the UE-to-RIS channels under the condition of the known RIS-to-BS channel,also using ANM to formulate the problem.In the second stage,multiple measurements are required,which can be obtained only by changing the RIS phase shifter.Due to the wired high-speed connection between BS and RIS,the proposed channel estimation method can further reduce time consumption by specialized mechanisms.Simulation results show that the proposed method works well in the considered scenarios.

Notations: A vector is denoted by a bold lowercase lettera,and a matrix is denoted by a bold capital letterA.(·)T,(·)*and (·)Hdenote the matrix or vector transpose,conjugate,conjugate transpose,respectively.Tr(X) is the trace ofX.IMdenotes theM×Midentity matrix,j=and CN×1denotes the space ofN×1 complex-valued matrices.For a square matrixS,S-1denotes its inverse (ifSis of full rank).⊗denote the Kronecker product,(·)†denotes the Moore-Penrose inverse,vec(A) is the vectorization ofA.The symbolℜ(·) denotes the real part.The inner product of vectorsx,yis defined as〈x,y〉=xTy*.The Frobenius inner product of two matricesX,Yis defined as〈X,Y〉F=Tr(XTY*).

II.SYSTEM MODEL

We explore an uplink mmWave multiuser communications scenario assisted by RIS.The direct link between the BS and the UEs is blocked,and the communicate with each other via the RIS,where there are both line-of-sight(LoS)links in BS-RIS and RIS-UE channels.As shown in Figure 1,more specifically the RIS consists ofNreflecting elements,and the BS is equipped withMantennas to serveKsingle-antenna users.Without generality,we consider both the BS and the RIS to consist of uniform linear arrays(ULA)s.

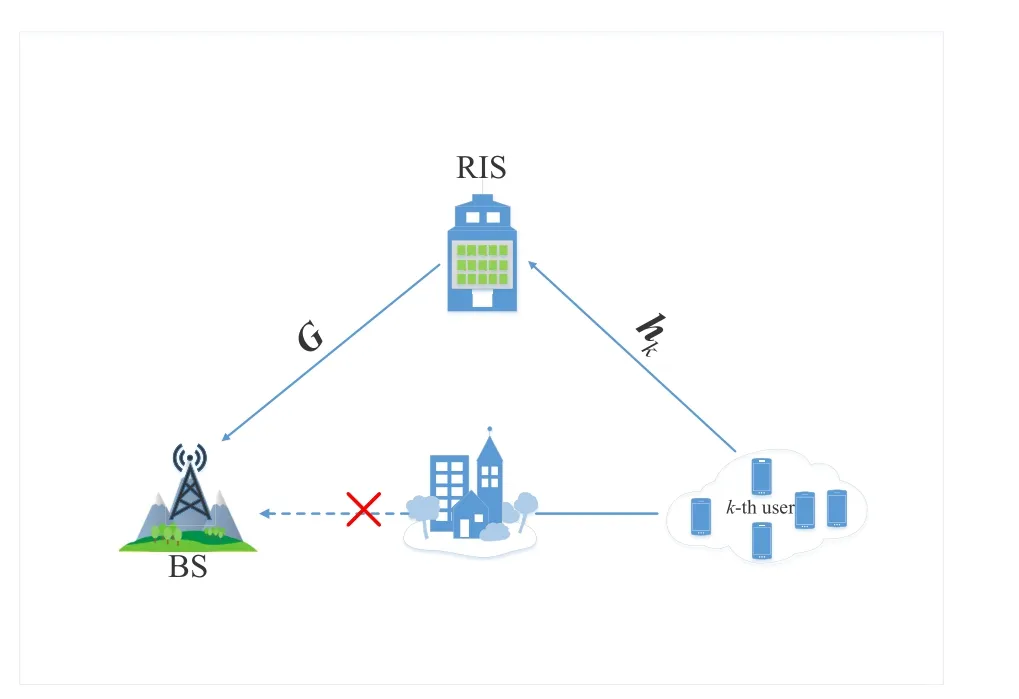
Figure 1.RIS-aided mmWave with blocked device-BS channels.

We assume a block-fading channel model where the channel is quasi-static in each block of length T.Lethk ∈CN×1andG∈CM×Ndenote the channels between the user k and the RIS,and the channel between the RIS and the BS,respectively.Define setK={1,...,K}.Due to the fact that both the BS and the RIS are fixed,it is assumed that there is only a LoS path among the BS-RIS[18].Thus,hkandGshould be given by

with the array response given as follow:

whereβlandγdenote the complex gains of the paths with the distribution ofβl,γ～CN(0,1),andLrepresents the number of paths between userkand RIS.θgtis the departure angle at RIS andθgris the arrival angle at the base station.When the channel estimation process,the k-th user transmits T training pilots from T time slotsxk ∈CT×1to the BS via the RIS.We denoteP∈CN×Nas the phase shifting matrix of the RIS,which is represented as

whereϕi,i=1,...,Nrepresents the phase of the RIS element.Finally,the received signal from userkat the BSYk ∈CM×Tcan be expressed as

whereNk～CN(0,σ2IM×T) is the additive white Gaussian noise andσ2is the power ofNk.Assuming there are K users,the received signalYcan be represented as

III.TWO-STAGE CHANNEL ESTIMATION

Figure 2 illustrates the fundamental concepts of the suggested channel estimating protocol.Where the“Pilot”and“Data”stand for the phases of uplink channel estimation and downstream data transmission at the BS side,respectively[19].Our research focuses on the estimation of the uplink channels for cascaded channels.Specifically,start by dividing the cascade channel for all users into two parts,the common channel,and the unique channel.In Phase I,the common channel for all users is estimated.Information about the common BS-RIS channel is extracted from all users’CSI estimates to reduce the pilot overhead of the next stage.Then,in the second phase,only one user-k’s channel to RIS is estimated.For convenience,we refer to this user as a typical user.Using the status information of the common channel obtained in the first stage,the channel information of the user to RIS can be easily obtained.

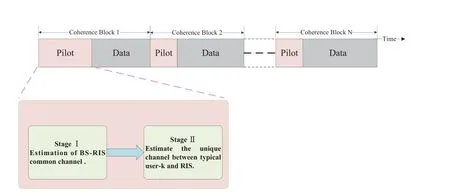
Figure 2.The adopted two-stage channel estimation protocol.

According to (5),it is aimed to estimateGandhkfrom the measurementsY.The first stage is to calculate the RIS-to-BS channel by estimating the AOA ofGand using the path-loss model,and the second stage is then estimatinghkusing the knownGobtained in stage one.

3.1 Estimating G

Based on(1),(5)can be rewritten as

In order to solve (7),we first reformulate it as a semidefinite programming problem.It can be rewritten as

The enhanced Lagrangian for this issue is provided by

whereρis the augmented Lagrangian parameter and Λk ∈C(M+1)×(M+1)are dual variables.Then,ADMM includes the subsequent iterations:

The cannonical dual window ˜gcan prevent the computation of matrix inversion in(15)as

The updates foru,v,Zk,and Λkcan be computed in parallel for each k,T†:CM×M →CMin the update forurepresents the pseudoinverse operator ofT,

The rest parameterγofGcan be estimated via the free-space path loss model[23]

whereL0,f,anddare measured in units ofdB,MHz,andkm,respectively,wherefsignifies the signal frequency anddis the spreading distance,such as the distance between BS and RIS.The path loss model gives us an estimate of the channel gain that is expressed as

Then the estimate ofGcan be obtained

3.2 Estimating hk

The equivalent SDP of(22)can be written as

where Toep(t2)∈CN×Ndenotes the Toeplitz matrix formed by the elements oft2,t2=

According to(23),the channel estimation ofhkcan be formulated as the following optimization problem:

whereµ ＞0 is the weight factor.In practice,we set

Equation(24)can be reformulated as a SDP and can be solved using SDP solvers,e.g.,CVX toolbox.By solving the problem(24),ˆhkis obtained.

3.3 Computational Complexity

In this paper,a two-stage channel estimation method is adopted.The first stage estimates the common channelGuses the ADMM algorithm with a complexity ofO(KMN).In the second stage,hkhas been estimated,with a complexity ofO(KN2).Based on the above algorithm,the total complexity isO(KN(M+N)).Secondly,the ALS algorithm proposed in [17],the complexity of ALS-based algorithm is dominated by involved matrix inverse computations: the computational complexities ofhkandGareO(N3+4N2M-NM) andO(N3+4N2K-NK),respectively.Thus,the total computational complexity of the ALS-based CE isO(2N3+4N2(M+K)-N(M+K)).Next,the VAMP algorithm proposed in [17],the VAMP-based algorithm is mainly dominated by matrix-vector multiplications the computational complexities ofhkandGareO(K(5N2-N))andO(M(5N2-N)),respectively.In summary,the total complexity of the VAMP-based CE isO(K+M)(5N2-N).Last,we analyze the complexity of the OMP algorithm,in which the complexity ofhkandGestimates areO(KMN2)andO(KN2),respectively.Thus,the total complexity of the OMP-based CE isO(KMN2+KN2).Finally,the computational complexity of the channel estimation algorithm involved is summarized in Table 1.

Table 1.Computational complexity of channel estimation algorithms.

3.4 Extended to Multi-Antennas User

As can be seen from above,when extended to multiple antenna users,the difference in formulating the channel estimation problem is that the atomic norm changes from one dimension to decoupled two dimensions.Therefore,the follow-up processing is similar to that in Sections 3.1 and 3.2.

IV.CRLB ANALYSES

The Cramer-Rao Lower Bound (CRLB) serves as a performance measure for our suggested CE approach because it is the lower bound of any unbiased estimator.As a result,in this part,we derive the CRLB for the estimation of the channel parameter based on[24,25].In the two-stage CE,the channelGusing the signals that were received at BS has been estimated in the first,and then we estimate the channelhusing the signals that were received at RIS.We additionally divide the computations of the CRLB into two parts in order to be consistent with our suggested two-stage CE approach.

The first stage of the proposed CE involves the estimation of the parametersη={γ,θgt,θgr},and the specifics of the derivations ofCRLB(η)=J(η)-1,whereJ(η) is the fisher information matrix (FIM) ofη.In Appendix A,including the specifics of how the FIM was derived,The parameters for the RIS-BS channelξ={βl,θl}are estimated during the second stage of the suggested CE method.Appendix B contains the specifics of theCRLB(ξ)=J(ξ)-1derivations of the FIM.

V.SIMULATION RESULTS

For the first experiment,as shown in Figure 3a,we consider the performance of the channel estimatingG.It can be found that in the case of signal-to-noise ratio(SNR)≤-5dB,the accuracy ofGestimation is not satisfied,but when it comes to the case of SNR＞-5dB,the NMSE falls down to lower than-12dB,which is considered precise enough.It can be seen from the simulation results that with the improvement of the signal-to-noise ratio,the performance is getting better and better,and with the increase of the number of LoS in the case of the same SNR,the NMSE is getting smaller and smaller,but when the signal-tonoise ratio increases,the performance difference under different paths gradually decreases.

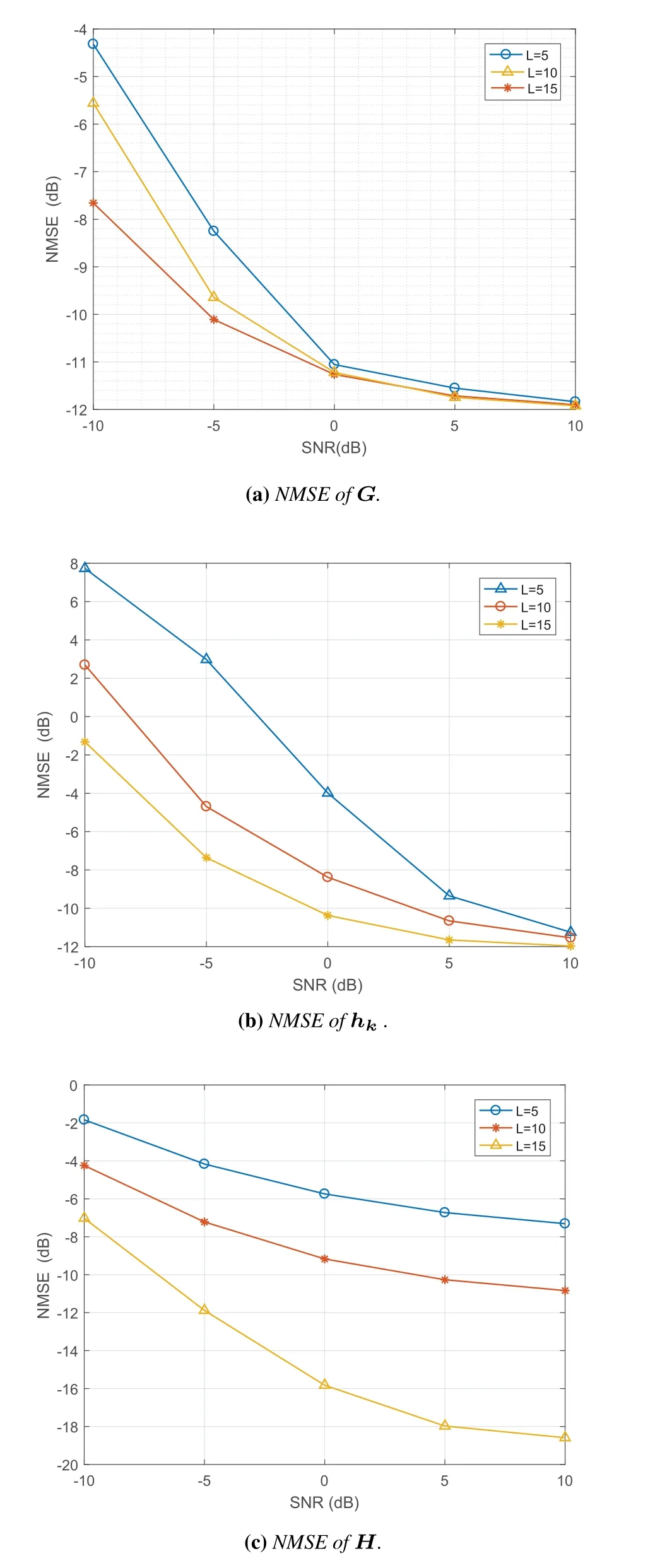
Figure 3.NMSE of G,hk and H estimation using the proposed method with measurement number of L=5,10,15 respectively.

As seen in Figure 3b,in the second experiment,we consider the resolution of the estimated information of channelhk.From the results,it is obvious that the curves have shown a similar tendency as Figure 3a.This is for the reason that the accuracy of ˆhdepends on that of the ˆG.On the other hand,the number of measurements also affects the results.From the figure,we can observe that its performance is significantly better than the other two whenL=15.

For the third experiment,as shown in Figure 3c,we consider the performance of channel estimatingH.Expect a similar tendency as Figure 3b,and the final result is strongly influenced by the number of the LOSL.It can be observed that Figure 3c does not increase with the signal-to-noise ratio of Figure 3a and Figure 3b,and the final simulation results of different channel numbers tend to be consistent.What we observed was that the simulation results of the different channel numbers did not converge as the signal-tonoise ratio increased.We could see that the results ofL=15 were significantly better than the other two,and that the NMSE reached-19 at SNR=10dB.

For the fourth experiment,as shown in Figure 4,we compare the performances of the proposed method and the orthogonal matching pursuit (OMP) method,ANM method,under the unified settings of the numbers of antennas and UEs,e.g.,K=4,M=16,N=16,L=5.From the simulation results,we can easily find that the proposed method achieves higher resolutions than that of the OMP method and ANM method,for the reason that the method we propose to denoise and extract the frequency information is based on the ANM,and the ADMM algorithm is used to solve the problem an off-grid method which obtains information directly from the continuous parameter domain.By contrast,the on-grid methods,e.g.,OMP,essentially discretize the continuous angle,and then search the closest point as the approximate value.These methods will lead to the basis mismatch problem in estimating continuous parameters,resulting in the decline of estimation accuracy.On the other hand,it can also be seen that the proposed method works well under low SNR conditions,which indicates its excellent denoising performance.We now compare our proposed method with the performance of the CRLB(more details can be found in Section IV,and the calculations/derivations are described in Appendices A and B).Although our method has achieved better performance compared to the literature,as shown in Figure 5,the gap between NMSE and CRLB of the proposed estimator indicates that there is still room for improvement in our method.

Figure 4.The proposed method is compared with OMP and ANM and analyzed as a whole.

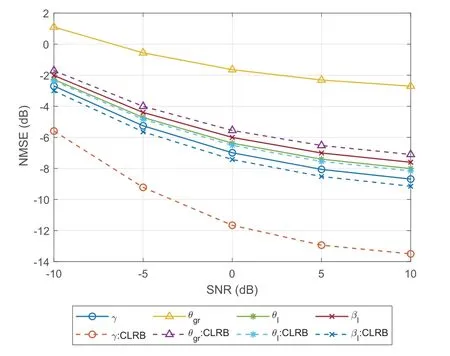
Figure 5.NMSEs of the channel parameters vs. CRLBs.

The NMSE performance comparison of the BUTAMP two layers algorithm,BAMP two layers algorithm[16],and the two-stage approach proposed versus the signal-to-noise ratio(SNR)is given in Figure 6.The parameter settings areM=16,K=5,L=10,andN=32,and the damping factorβin BAMP method is set 0.3.As can be seen from the figure,the NMSE performance of the first two scenarios is similar.Moreover,compared to these two algorithms,the proposed algorithm even slightly better than the two algorithms in the early stage,which is because ANM has strong denoising ability,but with the increase of signal-to-noise ratio,the performance of the algorithm proposed in this paper is slightly inferior to the two algorithms in[16],the reason is that we introduce parametersµin channel estimation,which has better robustness at low signal-to-noise ratio,but poor performance at high signal-to-noise ratio.

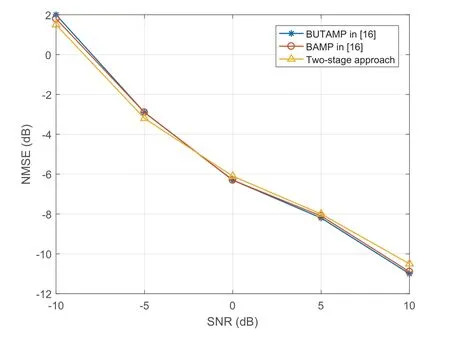
Figure 6.NMSE performance comparisons of BUTAMP in[16],BAMP in[16],and Two-stage approach.

The comparison of NMSE performance between ALS-based CE,VAMP-based CE [17],and the twostage approach proposed is shown in Figure 7.The parameter settings areM=8,K=5,L=8,andN=8.It can be seen from the figure that the two algorithms of ALS-based CE and VAMP-based CE have similar performance,and the two-stage approach proposed in this paper has better performance in the early stage because ANM has better denoising ability,but its performance is weaker than that of the two algorithms compared due to the influence of parameters in the later stage.

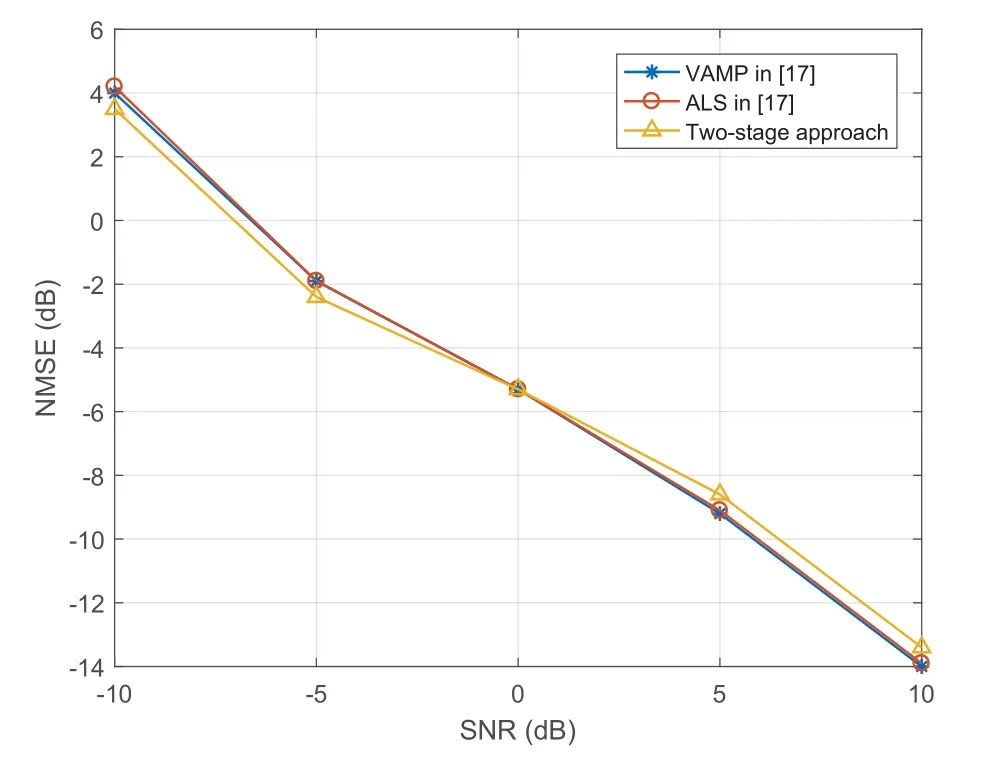
Figure 7.NMSE performance comparisons of VAMP in[17],ALS in[17],and Two-stage approach.

VI.CONCLUSION

In this paper,we have proposed a two-stage channel estimation method for multi-user uplink RIS systems that can accurately calculate the active users’ channel based on the ADMM and the free space path loss model.Simulation results indicate that the proposed method works well in the given scenarios.

APPENDIX

A CALCULATION OF THE CRLB: STAGE 1 OF CE

We will go over the CRLB calculations for the suggested CE technique in the sections that follow.At the initial stage of CE,we estimate the RIS-UE channel’s parameters,which are denoted by the notationη={γ,θgt,θgr}.The lower bound for the MSEs of the channel parameters inηis defined byCRLB(η),which is written as

whereJ(η) is the FIM.For instance,the observation vectory=vec(Y)follows Gaussian distribution withCN(µ1,σ2I),whereY=GPhkxT+N=Gu+Nandµ1is defined by

Using this premise,we can write the (l1,l2)thelement of FIM as

The derivatives ofµ1with respect to the channel parameters inηare described in the following step,after which the entries of the FIM are further derived.

A.1 Partial Derivatives

Regarding the channel parameters inη,we characterize the partial derivative ofµ1.

A.2 Calculation of Fisher Information Matrix

For the sake of simplicity,we merely specify the entries of the FIM elements as the following:

The derivatives ofµ1with respect toηare substituted,and the result is

The rest of the elements of FIM can be derived according to the same process.

B CALCULATION OF THE CRLB: STAGE 2 OF CE

At the second CE step,we aim to recover the RISUE channel’s parameters,which are specified asξ={βl,θl}.Keep in mind that the process of obtaining FIM elements and corresponding CRLBs is the same as the analysis in Appendix A.We assume that the observation vectory=vec(Y)follows Gaussian distribution withCN(µ2,σ2I),whereYH=ϱhkxT+Nand the meanµ2is expressed by

By making use of this supposition,we may create the FIMJ(ξ)as

The derivatives ofµ2with regard toξare developed in depth in the sections that follow.

B.1 Partial Derivatives

First,we develop the partial derivatives ofµ2with respect to the channel parameterθl.

B.2 Calculation of Fisher Information Matrix

We first calculate the entries of the elements in the principal diagonal.For instance,the (m,m)th entry ofJ(ξ)is given by

By substituting the derivatives ofµ2with respect toθl,we obtain

Similarly,we can obtain

It should be noted that the same process is used to calculate the(m,i)-thoff-diagonal elements.