Off-Grid Compressed Channel Estimation with ParallelInterference Cancellation for Millimeter Wave Massive MIMO

Liu Jinru,Tian Yongqing,Liu Danpu,Zhang Zhilong

Beijing Laboratory of Advanced Information Network,Beijing Key Laboratory of Network System Architecture and Convergence,Beijing University of Posts and Telecommunications,Beijing,100876,China

Abstract: Millimeter wave (mmWave) massive multiple-input multiple-output (MIMO) plays an important role in the fifth-generation (5G) mobile communications and beyond wireless communication systems owing to its potential of high capacity.However,channel estimation has become very challenging due to the use of massive MIMO antenna array.Fortunately,the mmWave channel has strong sparsity in the spatial angle domain,and the compressed sensing technology can be used to convert the original channel matrix into the sparse matrix of discrete angle grid.Thus the high-dimensional channel matrix estimation is transformed into a sparse recovery problem with greatly reduced computational complexity.However,the path angle in the actual scene appears randomly and is unlikely to be completely located on the quantization angle grid,thus leading to the problem of power leakage.Moreover,multiple paths with the random distribution of angles will bring about serious interpath interference and further deteriorate the performance of channel estimation.To address these off-grid issues,we propose a parallel interference cancellation assisted multi-grid matching pursuit(PIC-MGMP)algorithm in this paper.The proposed algorithm consists of three stages,including coarse estimation,refined estimation,and inter-path cyclic iterative interference cancellation.More specifically,the angular resolution can be improved by locally refining the grid to reduce power leakage,while the inter-path interference is eliminated by parallel interference cancellation(PIC),and the two together improve the estimation accuracy.Simulation results show that compared with the traditional orthogonal matching pursuit(OMP)algorithm,the normalized mean square error(NMSE)of the proposed algorithm decreases by over 14dB in the case of 2 paths.

Keywords: channel estimation;compressed sensing;inter-path interference;millimeter wave massive MIMO;off-grid;parallel interference cancellation

I.INTRODUCTION

In the era of fifth-generation mobile communications(5G),emerging applications such as the Internet of vehicles,the Internet of Things,virtual reality,and smart cities are developing rapidly,with surging demand for high data rates,capacity,and spectrum efficiency[1].However,the available spectrum of the sub-6GHz band is increasingly crowded and scarce,while the available resources of the millimeter wave(mmWave)band are abundant,with a large bandwidth to support the gigabit data rate [2].Therefore,mmWave plays an important role in 5G communication [3].Unfortunately,the mmWave frequency band is vulnerable to environmental influence because of its short wavelength.The path loss in free space is very large due to the effects of atmospheric absorption,rain failure,snow failure,and penetration loss,which is not suitable for long-distance communication[4].Therefore,it is necessary to combine key technologies such as massive multiple-input multiple-output (MIMO) antenna systems and hybrid beamforming to compensate for the path loss and improve the link gain[5].

The accurate acquisition of channel state information (CSI) is the key to the effective communication of the mmWave system.However,the use of massive MIMO antenna array increases the dimension of the channel matrix greatly,and there are many channel parameters to be estimated.Traditional channel estimation methods such as least squares(LS)[6,7]and minimum mean square error (MMSE) [8] are no longer applicable,and channel estimation has become a very challenging problem.Advantageously,the mmWave channel consists of only a few paths,which means that it shows strong sparsity in the angle domain or equivalent spatial frequency domain [9].To reduce the cost of channel estimation,the mmWave channel is usually modeled by the path’s azimuth angles of departure (AoDs),angles of arrival (AoAs),and path gain [10].Therefore,the problem of mmWave channel estimation is transformed from the estimation of a high-dimensional MIMO channel matrix to that of a small number of parameters including path directions and gains.

Given the channel sparsity of mmWave massive MIMO systems,compressed sensing technology[11-14] has been widely studied and applied in mmWave channel estimation [15].Robert W.Heath et al.propose an adaptive compressed sensing algorithm for beam training by using the designed hierarchical multi-resolution codebook in [16,17].The whole training process is divided into several stages,and beams of different widths are used in different stages until the required resolution is reached.The channel is estimated using OMP and its modified greedy algorithms,which perform greedy iterative selection on the columns of the sensing matrix to minimize the channel estimation error.The estimation accuracy and computational complexity depend on the quantization resolution of the angle grid[18-28].References[29-32]adopt the sparse Bayesian learning(SBL)channel estimation algorithm based on expectation maximization [33].This algorithm firstly regards the unknown parameter vector to be estimated as a random vector that conforms to a certain prior distribution,and determines the prior distribution according to the previous knowledge of the parameters sought.Then,based on the sample information,Bayesian rules are used to calculate the posterior probability distribution.Finally,the priori information and the posterior probability are integrated to infer the unknown parameters.The estimation accuracy of sparse Bayesian learning algorithm is higher than that of OMP algorithm,but the computational complexity also greatly increases.In the work [34-39],deep learning is applied to estimate the channel.By learning the characteristics of the channel through the proposed network training,and then the channel can be inferred accurately according to the trained network.

Although the above algorithms are simple and easy to implement,they ignore the off-grid problem in compressed sensing technology.In the above methods,only when the AoAs and AoDs of the real signal propagation paths are just located on the quantization grid points of the angle grid,namely on-grid,the recovered path angle is accurate.However,the path angle in the actual scene appears randomly and is unlikely to be completely located on the quantization grid.In this case,the grid mismatch occurs,namely off-grid,so the problem of power leakage will be generated.Although the grid mismatch can be alleviated by increasing the quantization resolution of the grid,the computational complexity also goes up.

To solve the off-grid problem,an improved off-grid SBL method is proposed in[40-42],which enables a good angle estimation in continuous AoAs/AoDs scenarios and avoids the serious grid mismatch problem.By taking advantage of the sparsity and correlation of the channel angle domain,a channel estimation algorithm combining compressed sensing and residual network is developed,which has low pilot overhead and computational complexity [43].A Newtonized Orthogonal Matching Pursuit (NOMP) algorithm is mentioned in literatures [44,45],which is a natural generalization of OMP.The method used in NOMP is Newton refinement,which uses the first and second derivatives at the coarse estimation point to perform a quadratic function approximation of the objective function,and then takes the poles of the quadratic model as the new iteration points.This process is repeated until the approximate poles satisfying the accuracy are obtained.In [46-50],Zhen G et al.take the grid quantization error in the compressed sensing framework into account,increase the resolution of grid quantization on the basis of the traditional OMP algorithm,and make the grid points gradually approach the real angle through continuous iteration to achieve accurate angle estimation.Among them,the algorithm in [48,49] is the baseline algorithm of this paper,which proposes a two-stage algorithm of multigrid orthogonal matching pursuit (MG-OMP),which is divided into the coarse estimation stage and the fine estimation stage.First,the initial AoAs/ AoDs are estimated using a lower resolution grid,and then a higher resolution grid is adaptively used around the initial AOAs/AODs for angle estimation,which can achieve higher channel estimation accuracy with lower computational complexity.References [51-53] adopt the atomic norm minimization (ANM) algorithm for channel estimation,which has excellent convex optimization properties and no accuracy constraints.Compared with OMP and other algorithms,which select codewords from finite codebook,that is,on-grid type,ANM algorithm searches in the range of infinite accuracy and is of gridless type.

Although the algorithms mentioned above can alleviate power leakage in the case of off-grid,they fail in the actual multi-path scenario.The reason is that offgrid power leakage will further incur inter-path interference when there more than one propagation paths existing in the channel.The mixed power leakage and inter-path interference are difficult to be mitigated,and greatly reduce the accuracy of angle estimation.

To address the above issue,we propose a parallel interference cancellation assisted multi-grid matching pursuit (PIC-MGMP) algorithm in this paper.The algorithm consists of three stages,and the first two stages are the same as those in the aforementioned references [47,48].The first stage is coarse estimation,which obtains the initial indexes of AoAs and AoDs through the correlation operation of the sensing matrix and residual.The second stage is refined estimation,where the angles around the initial AoAs and AoDs obtained in the first stage are locally refined with higher accuracy to make the angle estimation closer to the real angle.The third stage is inter-path cyclic iterative interference cancellation.In this stage,inspired by the parallel interference cancellation idea[54,55],the influences of other paths to the current path to be updated are subtracted from the received signal,thus obtaining a more accurate estimation on the angle of the current path.The simulation results show that the three-stage channel estimation algorithm proposed in this paper can significantly reduce the power leakage and inter-path interference due to off-grid in compressed sensing estimation,and effectively improve the accuracy of channel estimation.

The rest of the paper is organized as follows.Section II presents the system model.Section III formulates the compressed channel estimation problem.A three-stage channel estimation algorithm is designed in Section IV.In Section V,simulation results show the performance advantages of the proposed algorithm over the conventional methods,before the conclusion is presented in Section VI.

Notations:ais a scalar,the boldface lowercaseadenotes a vector,and the boldface uppercaseAdenotes a matrix.‖A‖Fis the Frobenius norm,whereas superscriptsAT,AH,A†denote the transpose,the Hermitian (conjugate transpose),and the Moore-Penrose inversion of a matrixA,respectively.[A](:,n)denotes then-th column of a matrixA,anddiag(a)is a diagonal matrix with the entries ofaon its diagonal.vec(A)is the vectorization operation according to the columns of the matrixA,andA⊗Bis the Kronecker product ofA,andB.「·is used to denote integer ceiling andCdenotes the set of complex number.E[·]is used to denote expectation operators.

II.SYSTEM MODEL

Consider the mmWave massive MIMO system model shown in Figure 1.For simplicity,a downlink single base station(BS)single user equipment(UE)communication system model with hybrid beamforming is assumed in this paper.However,according to channel reciprocity,the proposed scheme is also suitable for uplink scenarios.As shown in Figure 1,the BS is deployed withNtantennas andNt,RFradio frequency(RF) chains,and the UE is deployed withNrantennas andNr,RFRF chains.At the BS,the data and pilot signals are first transmitted toNt,RFRF chains through baseband processing,and then connected toNtantennas through phase shifters.At the UE,the signals received by theNrantennas are transmitted to the correspondingNr,RFRF chains through the phase shifter,and finally the original information is obtained through baseband processing.Here,it is assumed that the BS and UE communicate viaNsdata streams,such thatNs ≤Nt,RF ≤NtandNs ≤Nr,RF ≤Nr.

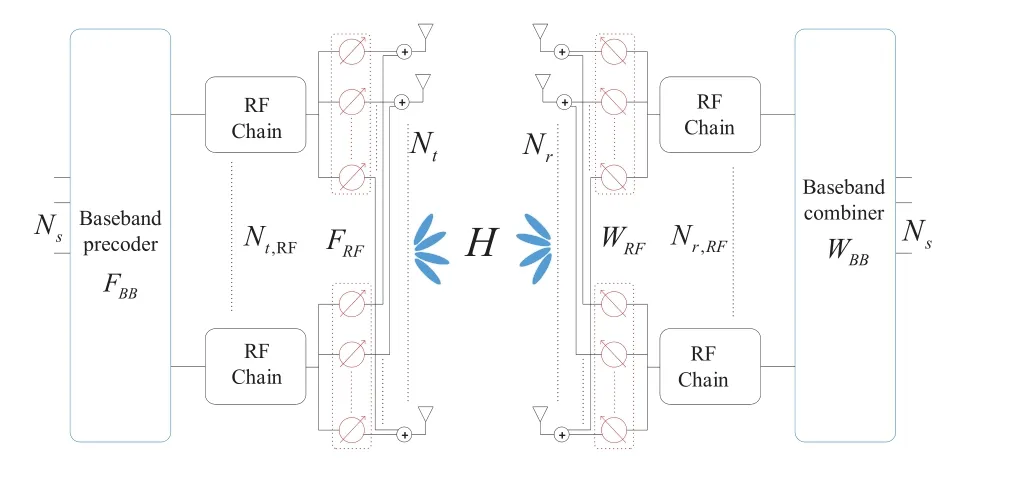
Figure 1.The architecture of a massive MIMO communication system.

In this paper,we assume that the baseband precoding matrixFBBwith dimensionNt,RF×Nsfollowed by the analog precoding matrixFRFwith dimensionNt×Nt,RF,then the transmittedNt×1 dimension signalxcan be represented by the following formula:

wheresrepresents theNs× 1 vector of transmitted pilot signal with E[ssH]=(Pt/Ns)INs,andPtis the average total transmit power of the transmitter.

When the transmitted signalxreaches the UE after being transmitted through the narrowband quasi-static fading wireless channel,theNr×1 dimension received signal on the UE can be expressed as:

whereHis the channel matrix inNr×Ntdimension andnis the additive Gaussian white noise vector subject to independent complex Gaussian distributionCN

At the UE,the analog combining matrixWRFwith dimensionNr×Nr,RFand the baseband combining matrixWBBwith dimensionNr,RF×Nscomplete the combining processing ofrand output the signal with dimensionNs×1:

Since mmWave propagates along a straight line basically and has poor diffraction ability,the scattering paths of the channel are relatively few.In this paper,it is considered that there are only a limited number of scatters in the channel,and a quasi-static narrowband geometric mmWave channel is considered,namely,Saleh-Valenzuela(S-V)channel.The channel model is as follows:

whereLrepresents the number of multi-path in the channel,αlis the complex gain corresponding to thel-th path.andrepresent the angle of arrival(AoA) and the angle of departure (AoD) of thel-th,respectively,and randomly distributed in the range[0,2π].arandatrepresent the response vector of the antenna array on the UE and the BS,respectively.When the antenna array is a uniform linear array (ULA),the array response vector is expressed as follows:whereλrepresents the wavelength,drepresents the distance between antenna array elements,and its value is generally half wavelength.

The channel model in Eq.(4) can be expressed in matrix form:

III.COMPRESSED CHANNEL ESTIMATION

Consider the mmWave massive MIMO system and the channel model described in Section II.Since the transmitter and receiver haveNt,RFandNr,RFRF chains respectively,Nt,RFandNr,RFbeams can be generated simultaneously.Therefore,when the transmitter sends the pilot signal s ofNsdata streams in an instant,the expression of the received signal at the receiver is shown in Eq.(3).AfterMtandMrtimes of beamforming and measurement at the transmitter and receiver respectively,Eq.(3)can be expressed as:

The analog beamforming vector can be taken from a predefined codeword set,such as BeamSteering codebook,DFT codebook,or the other design methods proposed in references [56,57].The DFT codebook is adopted in this paper.The weighting coefficientUx,ycorresponding to they-th codeword of thex-th antenna in the codebook is:

whereXis the number of antennas andYis the number of codewords.The codebook contains all the alternative codewords,each of which is an analog beamforming vector corresponding to a specific beam direction.The baseband beamforming matricesFBBandWBBare identity matrices.Nrepresents the noise matrix.

Due to the sparsity of mmWave channel in the angle domain,Eq.(6)can be expressed as the virtual channel in the angle domain,which is as follows:

Through the transformation of Eq.(10),the original channel matrixHcan be expressed as a sparse matrixHv,which can be quantized intoNr×Ntgrid points in the angle domain and the elements on each grid point represent the corresponding path gain.As shown in Figure 2(a),when the actual AoAs and AoDs of the channel just fall on the quantization grid,the number of non-zero values inHvis equal to the number of channel pathsL,andL ≪Nr×Ntis satisfied,that is,Hvis a sparse matrix.Therefore,the compressed sensing algorithm can be used to transform the estimation ofHvinto a sparse reconstruction problem,and the original channel matrixHcan be recovered according to Eq.(12):

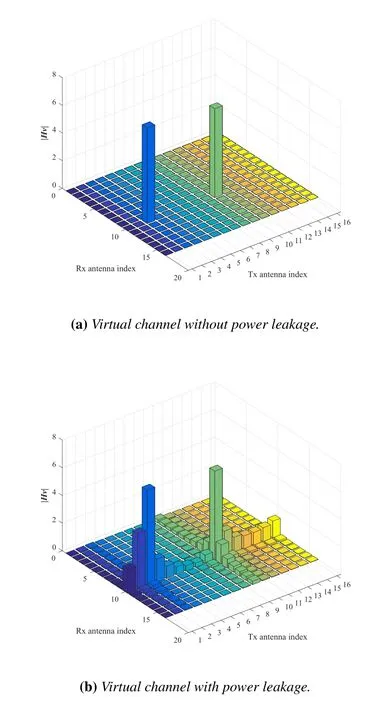
Figure 2.Virtual channel without/with power leakage.

In order to use the compressed sensing algorithm to realize the sparse reconstruction ofHv,substituting Eq.(12)into the received signal expression of Eq.(7)yields:

To exploit the sparsity of the channel,it is necessary to vectorize the received signalYin Eq.(13):

However,in actual scenes,the values of AoAs and AoDs are randomly and continuously distributed,while the quantization resolution ofandis limited.The quantization grid points inHvcan only represent limited pairs of fixed AoAs and AoDs combinations,so the random angle is unlikely to be completely located on the quantized grid points.In this case,power leakage as shown in Figure 2(b) will occur,that is,the number of non-zero values inHvis greater than the number of channel pathsL,and|Hv|gradually decreases from the true index position of the path along the Tx antenna index and Rx antenna index towards both sides.In addition,the position with more power leakage will cause power leakage again,which will lead to more non-zero values and also affect the performance of the final channel estimation.If the estimation accuracy is improved only by simply increasing the matrix dimensions of ¯Ar/¯Atand refining the grid inHv,it will lead to excessive computational complexity.Furthermore,when estimating the multipath channels,power leakage will also lead to serious inter-path interference,which will further deteriorate the performance of channel estimation.Therefore,how to improve the accuracy of grid quantization and eliminate the interference between multi-path is very important to improve the accuracy of channel estimation.

IV.PIC-MGMP CHANNEL ESTIMATION

According to the analysis in Section III,the continuous random distribution characteristics of AoAs and AoDs in the actual multi-path scenario will cause power leakage in the process of converting the original channelHinto the virtual channelHvin the angle domain,and further lead to inter-path interference,thus seriously affecting the performance of the final channel estimation.In addition,increasing the quantization resolution of the whole angle domain can improve the accuracy of channel estimation,but the computational complexity will increase significantly,and the interpath interference cannot be solved.

In order to solve the above problems,we propose a PIC-MGMP algorithm,which consists of three stages,namely coarse estimation,refined estimation,and inter-path cyclic iterative interference cancellation.For easy comprehension,the diagrams of the proposed estimation algorithm are shown in Figure 3,in which the black dots represent the actual paths and the red dots represent the estimated paths.Firstly,the OMP algorithm is used to perform correlation operations on the sensing matrix and residuals,so as to obtain the initial indexes of AoAs and AoDs.Then,according to the obtained initial indexes,the local grid refinement method is used to improve the quantization resolution of the initial angles,so as to reduce the power leakage.Finally,after estimating the angles of all paths,the PIC idea is used to subtract the influence of other paths to the current path to be updated from the received signal,thus obtaining a more accurate estimation on the angle of the current path.

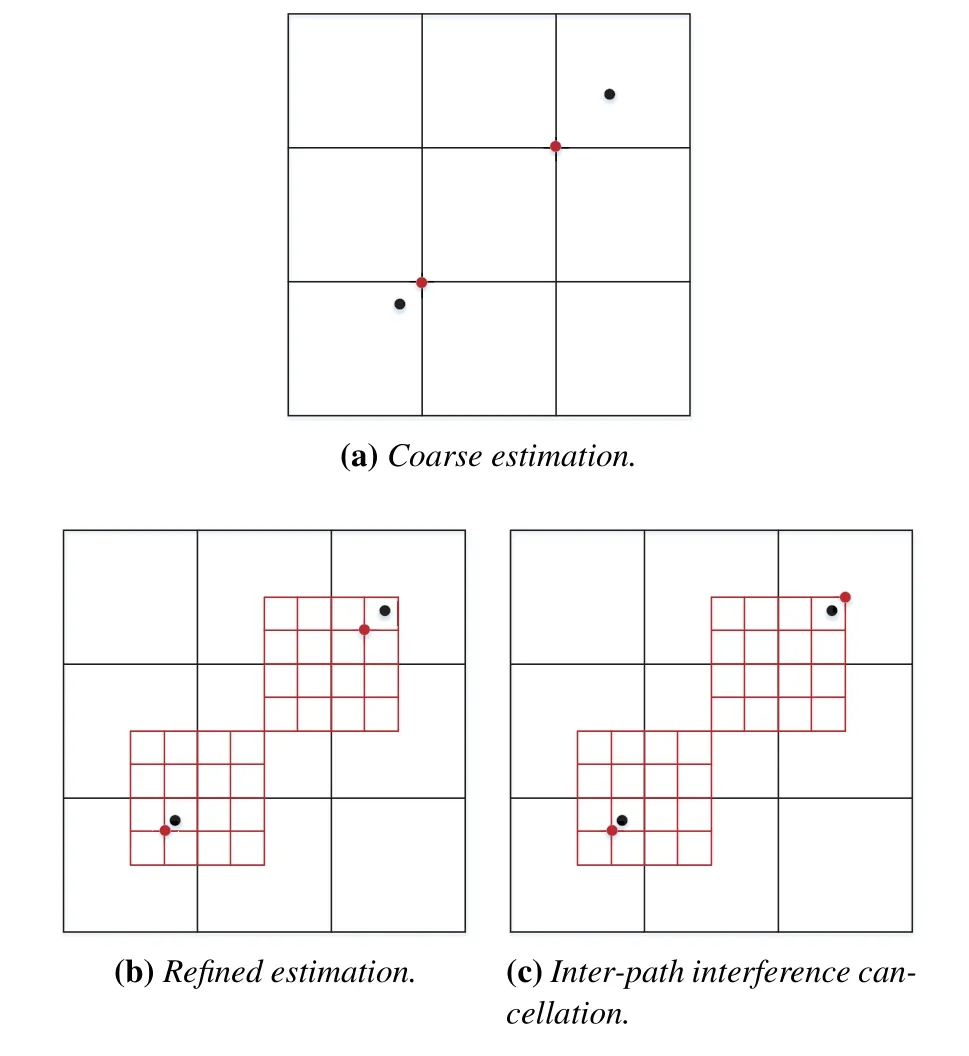
Figure 3.The diagrams of the proposed estimation algorithm.

In the process of communication,the receiver completes the channel estimation according to the received signal and the pilot transmitted by the transmitter.It is assumed that the number of channel paths is known to beLand the residualbis initialized toyv.In the proposed PIC-MGMP channel estimation algorithm,we successively estimate the AoA/AoD of each path in the channel,and the detailed calculation steps are described as follows.

(1) Coarse estimation stage.Calculate the inner product of each column of the sensing matrixΦand residualb,and take the column index with the largest absolute value of the inner product asλmax,and the column with the largest absolute value of the inner product is also the column with the largest correlation value.The expression is as follows:

where,βmaxis the maximum correlation value,φirepresents thei-th column of the sensing matrixΦ,andN=NrNt.According toλmax,the initial index of AoA/AoD of thel-th path corresponding to this column can be calculated,which are respectively denoted as

Then enter the next iteration of the current channel path estimation until the stop condition of the following formula is satisfied:

where,βnewandβlastrespectively represent theβmaxof the current iteration and the last iteration calculated according to Eq.(15),andεis a preset threshold.After several iterations,the AoA/AoD and the estimation of the sensing matrix column of the currentl-th path are calculated and saved as follows:

Then,the influence of all estimated paths is subtracted from the received signal using the least square method to update the residual:

Through the same operation of Eq.(15)-(22),we can successively obtain the AoAs/AoDs estimations ofLpaths.

(3) Inter-path cyclic iterative interference cancellation stage.After obtaining the angle information of allLpaths,the influences of other paths to thel-th path to be updated are subtracted from the received signal according to the following formula,and the residual is calculated:

whereΦdelis the sensing matrix of the path to be deleted,and[]represents an empty vector.After the residual is calculated,the angle information of the currentl-th path is updated according to Eq.(15)-(22).Save the updated AoA/AoD and the sensing matrix column of the current path according to the following formula:

At this point,the algorithm ends.For simplicity,the main steps of the proposed algorithm are summarized,as shown in Algorithm 1.

In addition,the algorithm proposed in this paper aims to improve the accuracy of channel estimation,so its computational complexity will be improved.In order to achieve a trade-off between estimation performance and computational complexity,the computational complexity of OMP,MG-OMP,PIC-MGMP,SBL and ANM algorithms are briefly analyzed below.

According to Eq.(15),the computational complexity of calculating the inner product of the sensing matrixΦand the residualbin the first stage of coarse estimation isO(NsMtMrNtNr).In the second stage of refined estimation,the complexity of computing the local sensing matrix using Eq.(17) isO(Nt(2R+1)Mt+NrNsMr(2J+1)+(2J+1)2NsMtMr),similarly,the computational complexity of the inner product of the local sensing matrixand the residualbisO(NsMtMr(2J+1)2).Thus,the complexity of OMP and MG-OMP algorithms can be obtained asO(NsMtMrNtNrL) andO((NsMtMrNtNr+Nt(2J+1)Mt+NrNsMr(2J+1)+2(2J+1)2NsMtMr)NiterL)respectively,whereNiteris the number of local refinement iterations when Eq.(20) is satisfied.After a round of the interpath cyclic iterative interference cancellation stage is performed,the algorithm complexity is 2NiterLtimes of the sum of the first stage and the second stage,that is,the complexity of PIC-MGMP algorithm isO((NsMtMrNtNr+Nt(2J+1)Mt+NrNsMr(2J+1)+2(2J+1)2NsMtMr)2NiterL).The update rules for the hyperparameters in the SBL algorithm mainly depend on the inverse calculation of the posterior weight covariance matrix,which is actually a Chorisky decomposition with a computational complexity ofO((NtNr)3).Therefore,the complexity of the SBL algorithm isO((2(NtNr)2NsMtMr+(NsMtMr)2NtNr+2(NtNr)3)Niter) [42].In the ANM algorithm,the semidefinite programming solver requires approximatelyO((NtNr)3+(NtNr)2)=O((NtNr)3)steps for each iteration,anditerations are performed at most.Therefore,the computational complexity of the ANM algorithm isO((NtNr)3.5log(1/ε)) [53].To make it more intuitive,the computational complexity of OMP,MG-OMP,PIC-MGMP,SBL and ANM algorithms are shown in Table 1.

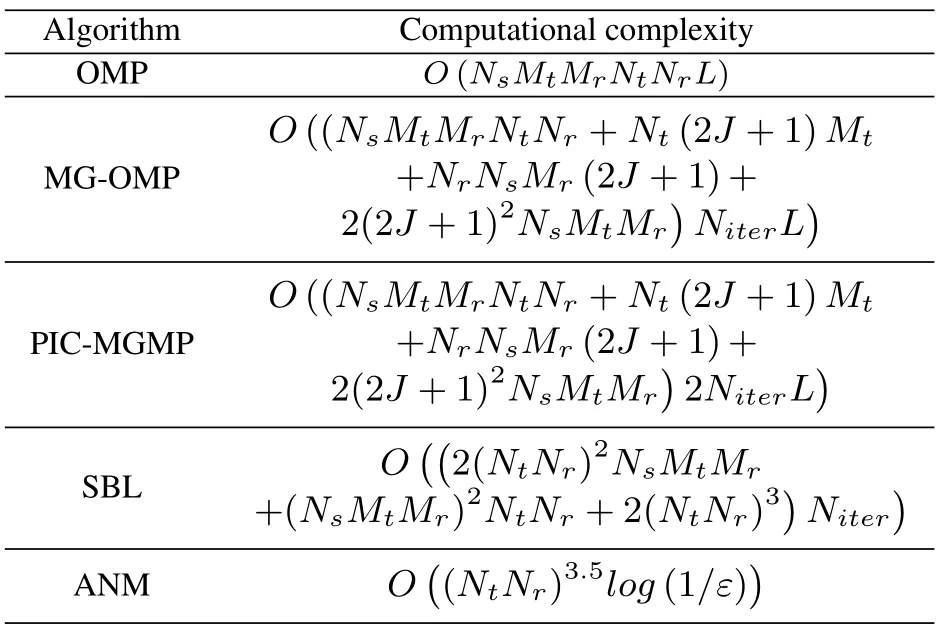
Table 1.Computational complexity.

V.SIMULATION RESULTS

In order to more directly observe the differences between the performance of different algorithms,MATLAB Monte Carlo simulation is used to compare the proposed algorithm with other OMP algorithms and MG-OMP algorithms.The simulation configurations are shown in Table 2.

Table 2.Simulation configurations.

The normalized mean square error(NMSE)of channel estimation is the main metric used to evaluate the performance of the algorithms.The expression of NMSE is defined as follows:

whereHrepresents the ideal original channel matrix,Hestrepresents the estimated channel matrix.

Figure 4 compares the impact of SNR on the NMSE of different algorithms in the case ofL=2/3/4 respectively.The number of antennas is configured as 32× 8,and the number of RF chains at the transmitter and receiverNt,RF=Nr,RF=6.It can be observed that the performance gap between the proposed algorithm and other algorithms increases gradually with the increase of SNR,but it is always better than other algorithms.Specifically,the OMP algorithm does not consider the influence of random angle distribution,and the quantization resolution remains unchanged from beginning to end.It only estimates the angle according to the initial quantization grid accuracy,resulting in the worst NMSE.MG-OMP algorithm only considers the effect of power leakage but does not consider the problem of inter-path interference,so its performance is improved compared with the OMP algorithm,but there is still performance loss.The performance of the proposed algorithm is better than that of the other two algorithms because both power leakage and inter-path interference are considered.SBL and ANM algorithms do not take channel sparsity as a priori information,so the estimation accuracy has a certain decline compared with the proposed algorithm.Moreover,since the noise variance is also iteratively updated as an unknown parameter in the SBL algorithm,the performance of the SBL algorithm decreases compared with the ANM algorithm.In addition,it can be seen from Figure 4 that the more paths there are in the channel,the higher the NMSE of the channel estimation algorithm is.This is because,with the increase of the number of paths,the inter-path interference of the channel gradually increases,which degrades the performance of the channel estimation algorithm.

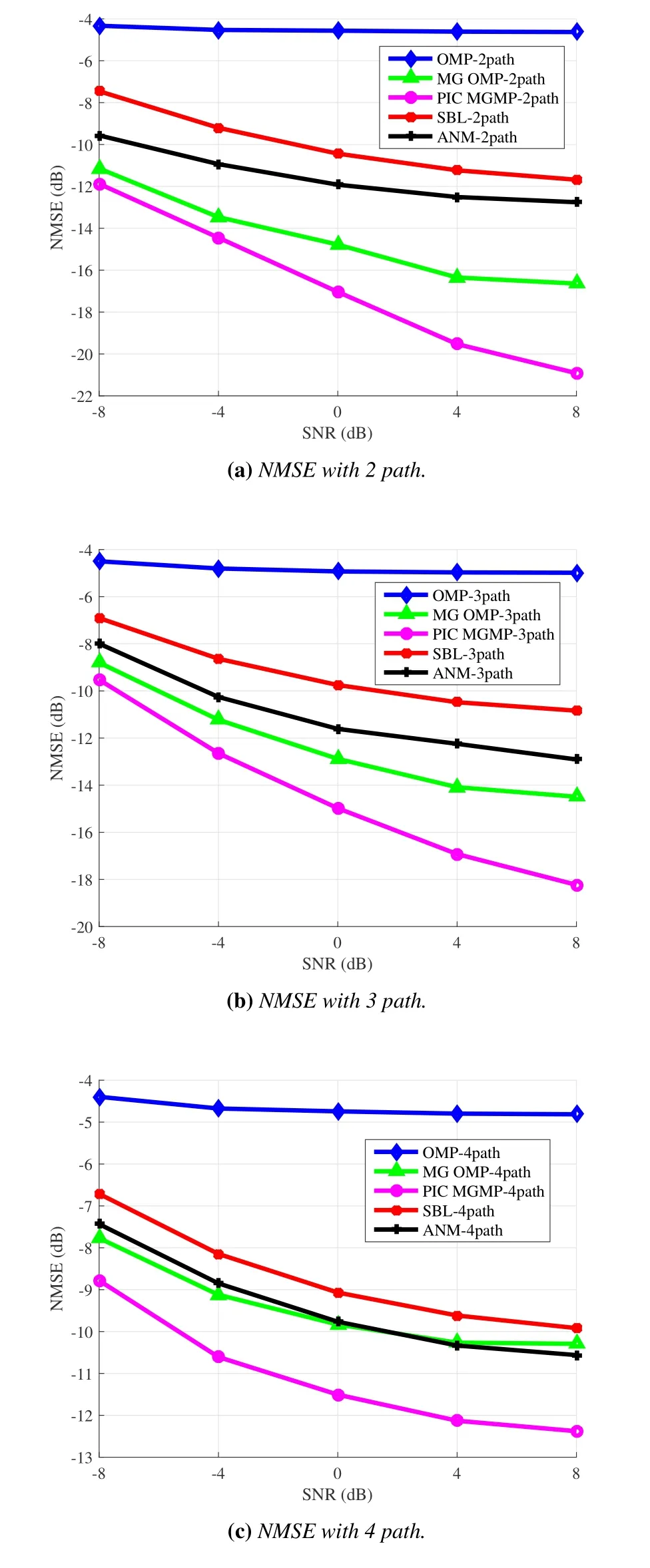
Figure 4.NMSE of different channel estimation algorithms with different path numbers v.s. SNR.

Figure 5 compares the variation trend of NMSE with SNR under different antenna configurations of the transmitter and receiver with different algorithms.The number of antennas is 32×8/32×16/64×8/64×16 respectively,and the number of pathsL=3.Simulation results show that the channel estimation performance of all algorithms improves with the increase of the number of antennas,and the proposed algorithm is always better than other algorithms.This is because with the increase in the number of antennas,the gain of analog beamforming is higher,and the resolution of angle quantization is also higher,resulting in a more accurate angle estimation of the path.

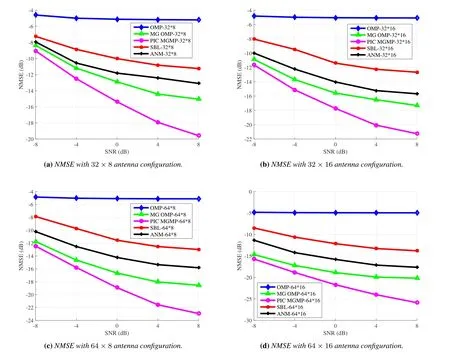
Figure 5.NMSE of different channel estimation algorithms with different antenna configurations v.s. SNR.

Figure 6 compares the NMSE with SNR under the configuration of different RF chains at the transmitter and receiver with different algorithms.The number of RF chains is respectively configured as 4×4/6×4/6×6.The number of antennas is configured as 32×8,and the number of pathsL=3.From the simulation results in Figure 6,it can be observed that the channel estimation performance of the algorithm proposed in this paper is always better than other comparison algorithms,and the NMSE of all algorithms decreases with the increase of the number of RF chains.This is because,with the increase in the number of RF chains,the transmitter and receiver can generate more training beams at the same time,so as to achieve more angle scanning and improve the accuracy of channel estimation.

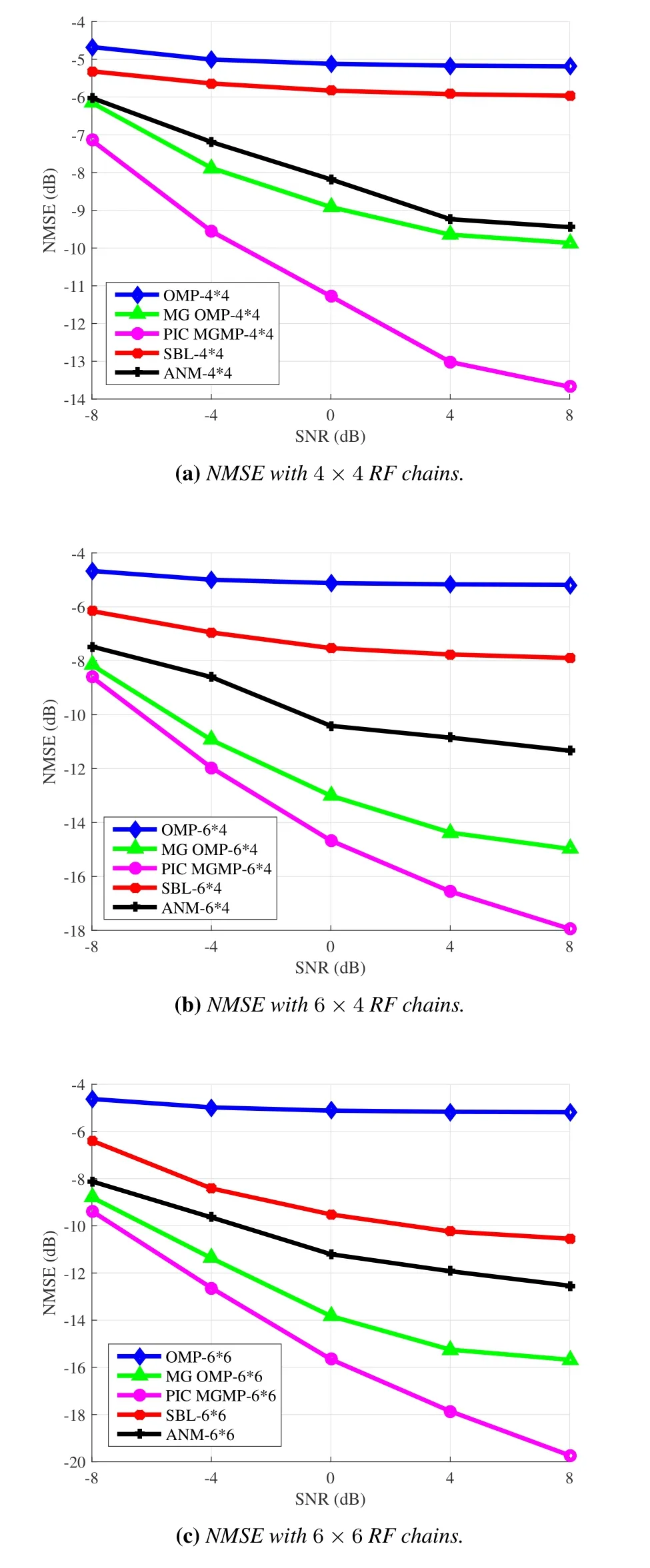
Figure 6.NMSE of different channel estimation algorithms with different RF chains v.s. SNR.

Figure 7 compares the computational complexity of different algorithms with different path numbers and antenna configurations.In Figure 7(a),the number of pathsL=1/2/3/4/5,the number of antennas is configured as 32×8,and the number of RF chains at the transmitter and receiverNt,RF=Nr,RF=6.In Figure 7(b),the number of pathsL=3,the number of antennas are configured as 32×8/32×16/64×8/64×16,and the number of RF chainsNt,RF=Nr,RF=6.As can be seen from Figure 7,the computational complexity of OMP,MG-OMP,PIC-MGMP,SBL,and ANM algorithms increases successively,and the computational complexity of these algorithms increases gradually with the increase of the number of paths and antennas.

VI.CONCLUSION

In this paper,a channel estimation algorithm based on compressed sensing for grid local refinement and inter-path cyclic iterative interference cancellation in mmWave massive MIMO antenna system is proposed.Aiming at the problem that the path angle is random and cannot be completely located on the angle quantization grid in the real mmWave multi-path channel scene,a three-stage grid local refinement algorithm is proposed.The first is the coarse estimation stage of using the OMP algorithm to estimate the initial angle.Then is the refined estimation stage of higher precision local quantization based on the initial angle.Finally,the inter-path cyclic iterative interference cancellation stage,which subtracts the influence of all paths other than the current path to be updated from the received signal based on the results estimated in the refined estimation stage,removes the inter-path interference and updates the angle estimation of the current path.Simulation results show that the proposed algorithm can effectively reduce the power leakage and inter-path interference in the case of multi-path channels with random angle distribution based on compressed sensing estimation,and improve the channel estimation accuracy with low computational complexity.

ACKNOWLEDGEMENT

This work is supported in part by the Beijing Natural Science Foundation under Grant No.L202003,the National Natural Science Foundation of China under Grant U22B2001 and 62271065,and the Project of China Railway Corporation under Grant N2022G048.