Improved Segmented Belief Propagation List Decoding for Polar Codes with Bit-Flipping

Mao Yinyou ,Yang Dong ,Liu Xingcheng,,3,* ,Zou En

1 School of Electronics and Information Technology(SEIT),Sun Yat-sen University(SYSU),Guangzhou 510006,China

2 School of Information Science,Guangzhou Xinhua University,Guangzhou 510520,China

3 Southern Marine Science and Engineering Guangdong Laboratory(Zhuhai),Zhuhai 519080,China

Abstract: Belief propagation list (BPL) decoding for polar codes has attracted more attention due to its inherent parallel nature.However,a large gap still exists with CRC-aided SCL(CA-SCL)decoding.In this work,an improved segmented belief propagation list decoding based on bit flipping (SBPL-BF) is proposed.On the one hand,the proposed algorithm makes use of the cooperative characteristic in BPL decoding such that the codeword is decoded in different BP decoders.Based on this characteristic,the unreliable bits for flipping could be split into multiple subblocks and could be flipped in different decoders simultaneously.On the other hand,a more flexible and effective processing strategy for the priori information of the unfrozen bits that do not need to be flipped is designed to improve the decoding convergence.In addition,this is the first proposal in BPL decoding which jointly optimizes the bit flipping of the information bits and the code bits.In particular,for bit flipping of the code bits,a H-matrix aided bit-flipping algorithm is designed to enhance the accuracy in identifying erroneous code bits.The simulation results show that the proposed algorithm significantly improves the errorcorrection performance of BPL decoding for medium and long codes.It is more than 0.25 dB better than the state-of-the-art BPL decoding at a block error rate(BLER)of 10-5,and outperforms CA-SCL decoding in the low signal-to-noise(SNR)region for(1024,0.5)polar codes.

Keywords: belief propagation list (BPL) decoding;bit-flipping;polar codes;segmented CRC

I.INTRODUCTION

POLAR codes,proposed by Arikan[1],is a first channel coding scheme that can be proven to theoretically achieve the channel capacity over binary-input discrete memoryless channels(B-DMCs)asymptotically.In recent years,polar codes have been selected as the standard codes for the fifth-generation(5G)enhanced mobile broadband (eMBB) scenario [2].Although the successive cancellation (SC) decoding algorithm as the basic decoding algorithm of polar codes,could prove the capacity achievement property,its errorcorrection performance for practical code lengths is poor.

Then,to meet the high reliability and low delay requirements of 5G and the next generation of mobile communication systems,many decoding algorithms have been proposed to improve the error correction performance of polar codes.One of the proposed algorithms,the SC list (SCL) [3] decoding algorithm,which maintainsLcandidate codewords by using a group of SC decoders,can significantly improve the error-correction performance of SC decoding.However,there is still a non-negligible gap with low-density parity-check (LDPC) codes,a selected coding scheme for other scenarios of 5G.To address this problem,the CRC-aided SCL (CA-SCL) decoding algorithm was proposed [4].The CA-SCL decoding enhance the efficiency of selecting the correct codeword by concatenating the cyclic redundancy check(CRC)codes,and improve the error-correction performance compared with the SCL algorithm,exhibiting the superior performance over LDPC codes under certain conditions.Another SC-based decoding algorithm,SC-Flip (SCF) decoding,mitigates error propagation by flipping the first error-prone bits in SC decoding [5].SCF decoding improves the errorcorrection performance in medium-to-high signal-tonoise (SNR) regions,and its average computational complexity is close to that of SC decoding[6].However,the performance improvement is limited and the latency is too high due to its several SC decoding attempts.

All of these decoding algorithms are serial in nature.Therefore,they will suffer from higher decoding latency and lower throughput when the code length is long enough.Compared with these serial-based decoding algorithms,belief propagation (BP) [7] decoding has attracted much attention due to its characteristics of parallelism,soft-in-soft-out,and hardware friendliness[8].However,similar to SC decoding,the error-correction performance of BP decoding is also not ideal.For this reason,a variety of improved decoding algorithms have been proposed to improve the decoding performance.One way is to retain the characteristics of soft-in-soft-out but change the decoding schedule to serial,such as in the soft cancellation(SCAN)decoding algorithm[9],a soft-output version of SC decoding.The other proposed iterative decoding algorithm,combining the adjustable SCL(ASCL)[10]decoding with SCAN decoding,called the iterative adjustable soft list(IASCL)algorithm[11],improved the decoding performance as the number of iterations increased.Although the former obtains limited performance gain,it loses the characteristic of parallelism.And the latter’s complexity is so high that the performance improvement could be ignored.In addition,there is a concatenated decoding algorithm that uses LDPC codes as outer code to protect the insufficient polarized information bits of polar codes [12].Although the decoding performance of the concatenated coding scheme has been improved,the computational complexity is also increases,and the hardware implementation cost of the two different decoders in the subsequent concatenated decoding algorithm is too high.Another representative approach to improve BP decoding performance is BP flip (BPF) decoding [13],which identifies error-prone information bits by utilizing a fixed critical set and the decoding information,e.g.,the log-likelihood ratio(LLR),while maintaining the parallel nature of BP decoding.However,BPF decoding suffers limited improvement of errorcorrection performance from the inaccurate identification of bit errors.Consequently,there is an urgent need for a novel BP decoding algorithm that can improve its decoding performance and retain the parallel characteristics at the same time.

The BP list(BPL)decoding algorithm has been proposed in this situation[14].On the one hand,similar to SCL decoding,the error correction performance of BPL decoding can also be close to the maximum likelihood decoding when the number of lists is large.On the other hand,unlike SCL decoding,each decoder independently decodes the same codeword and decoding operation is carried out simultaneously,which means that the parallel characteristic of the BP algorithm is preserved to the greatest extent.Nevertheless,after adding CRC protection,there is also a substantial performance gap between CA-SCL decoding and BPL decoding,which results in a huge space for improvement of BPL decoding.Based on this situation,after concatenation of CRC code,Marvin Geiselhart et al.proposed a CRC-aided BP List (CA-BPL) decoding algorithm by using the additional error-correction capabilities of the outer CRC code [15].After the codeword decision,the two distinct CRC decoding algorithms: the Bahl-Cocke-Jelinek-Raiv (BCJR) decoding or the sum product algorithm (SPA) decoding based on the CRC encoding structure and the check matrix of CRC code,will be utilized to improve the performance of BPL decoding.This design makes the error-correction performance of CA-BPL decoding close to that of CA-SCL decoding in the case of short codes.However,when the code length becomes larger,there is still a certain performance gap between CABPL decoding and CA-SCL decoding since the error correction capability of CRC code is weak.Moreover,the two different decoders of CA-BPL also increase the computational complexity and make the hardware implementation cost too high.

In the proposed higher-order generalized BPF with merged set(GBPF-MS) decoding [16],we found that the performance of BP decoding would be greatly improved if the error-decoded bits could be flipped accurately.In particular,segmented multi-CRC aided applications [17] have achieved great successes in SCF decoding [18] and SCL decoding [19,20].The method of segmented decoding is worthy of further research to improve the performance of BPL decoding.However,all of these existing segmented decoding algorithms are designed for decoders with serial scheduling,such as SCF or SCL decoding.These segmented decoding algorithms will not be directly applicable to decoders with parallel scheduling.To the best of our knowledge,no segmented decoding algorithm has been designed for BPL decoding.

Accordingly,in this work,inspired by the enormous progress in the latest work about soft cancellation bitflip (SCAN-BF) decoding[21] and the BP correction(BPC) decoder [22],a new segmented BPL decoding algorithm with bit-flipping(SBPL-BF)is proposed.In the proposed algorithm,the distribution of error bits under BPL decoding is studied,then the information bits are partitioned according to the error distribution and the flipping set is also constructed by these bit error distributions.Moreover,unlike the BPC algorithm that establishes the flipping set(FS)only by choosing indices by theminLLRmethod,the proposed algorithm utilizes the aided H-matrix of polar code to correct a code bit.Furthermore,the proposed decoding algorithm does not need to use BCJR or SPA decoding,which results in a lower complexity and an easier hardware implementation.The contributions of this article are as follows:

• The bit error distribution under BPL decoding is shown,then a flipping set and a segmented approach based on this bit error distribution are constructed.The designed segmented approach is more suitable for the parallel nature of BPL decoding and it enlarge the identification that the information bits could be decided correcly and reduce the additional decoding attempts for bit flipping.

• Genie-aided BPL decoding is discussed with respect to the performance bound that BPL decoding with bit-flipping could achieve,demonstrating that the error-correction performance of an ideal bit-flipping scheme for BPL decoding could superior the CA-SCL decoding.

• A higher-order generalized segmented bit flipping scheme for BPL decoding(SBPL-BF)is proposed,and the segmented multiple bit-flipping procedure is described.Considering the multiple BP decoders in BPL decoding,multiple indices with the same order for performing bitflipping could be carried out in one decoding attempt.Compared with GBPF-MS decoding,the proposed algorithm could significantly reduce the additional decoding attempts.Meanwhile,to accelerate the decoding convergence,the correct bits identified by the CRC code are also assigned to the initial LLR.Furthermore,to reduce the computational complexity,a flexible and effective method of assigning the initial LLR to an error segment is designed in high-order (where the order is larger than 2)flipping attempts.

• For the first time in BPL decoding,bit-flipping operation occurred in the received codeword.With the aid of the H-matrix of polar code,the identification which code bits are erroneous is enhanced,and it promotes the reliability of the received codeword and improves the performance of each decoder in BPL decoding.

The proposed decoding algorithm is verified over the AWGN channel.Compared with the state-of-the-art improved BPL decoding algorithm,the simulation results show that the error-correction performance of BPL decoding is greatly improved.Especially in the case of medium-long codes,the performance of the proposed algorithm is close to that of CA-SCL decoding,while the decoding latency and throughput are much better than those of the CA-SCL algorithm.

The rest of this paper is organized as follows: Section II introduces the preliminaries about polar codes,BPL decoding and existing BPF decodings.In Section III,the bit error distribution of BPL decoding is shown,and then the designed segmented approach and the constructed flipping set is proposed.In Section IV,the proposed higher-order SBPL-BF decoding algorithm is described and shown,together with its achievable performance bound.Section V describes the bitflipping scheme in the estimated received codeword.Numerical results are provided in Section VI.Finally,Section VII concludes this article.

II.PRELIMINARIES

2.1 Polar Codes

In modern communication systems,polar codes are obtained by combining and decomposingNindependent channels to obtainNpolarized channel copies,and each copy is also called the bit channel of the polar codes,where theNindependent channels may be considered asNcopies of the practical channel.When the numberNtends to infinity,some of the bit channels tend to be noiseless channels with polarized channel capacities approaching 1,and the other portion will tend to be noisy channels with polarized channel capacities approaching 0[1].Usually,for the positions of the noisy channels,the bit sequence that both the transmitter and receiver have known(usually set to zero) is used,and these bits are called frozen bits.Then,for the positions of the noiseless channels,the information sequence is transmitted.If the source vectoruconsists ofKoriginal information bits and (N-K) frozen bits to form a polar codewordx={xi},i ∈{1,...,N},then we havex=uG,whereGis the code generator matrix.The positions of the noiseless channels are defined as setA,and remaining positions are defined as setAc.The generator matrixGis composed ofG=whereand⊗nis then-th Kronecker power ofF2.

2.2 BP and BPL Decoding

Affected by the outstanding performance of BP decoding in LDPC codes[23],Arikan proposed the BP decoding algorithm for polar codes after he designed the polar codes and the SC decoding algorithm[7].Unlike the BP decoding of LDPC code iterating in the Tanner graph,which is based on the check matrix [24],the BP decoding of polar code is calculated in the factor graph,which is based on the generator matrix.

Figure 1 gives the factor graph ofN=8 polar codes[8],where the nodes of the factor graph are labeled with paris of integers(i,j),1≤i ≤n+1,1≤j ≤N.From the decoder’s perspective,the nodes of the left-most side connect with the source,and the nodes of the right-most side connect with the channel.Moreover,two types of LLR messages propagate in the factor graph: the left-directed messagethat propagates from the right side to the left side and the right-directed messagethat propagates from the left side to the right side.Meanwhile,the updating calculation is completed in the process element (PE)in the factor graph,as shown in Figure 2.The polar code with lengthNincludeslogNPE modules.The soft message of each node is updated by(1)[8].

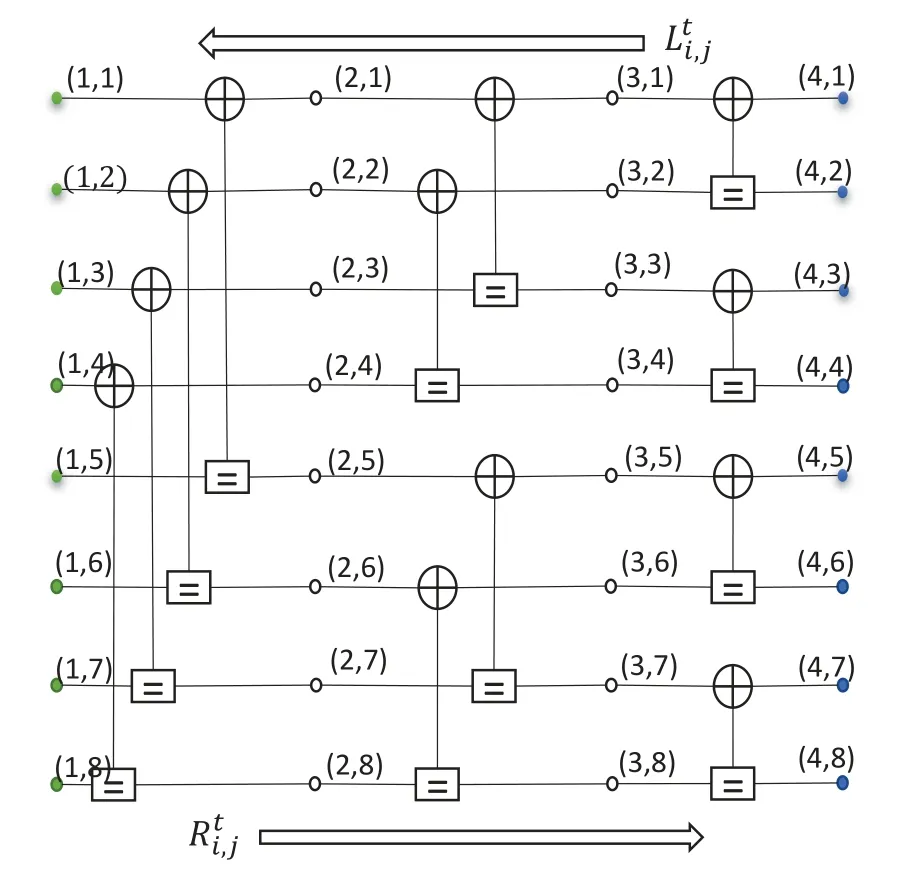
Figure 1.The factor graph for the transformation F⊗3.

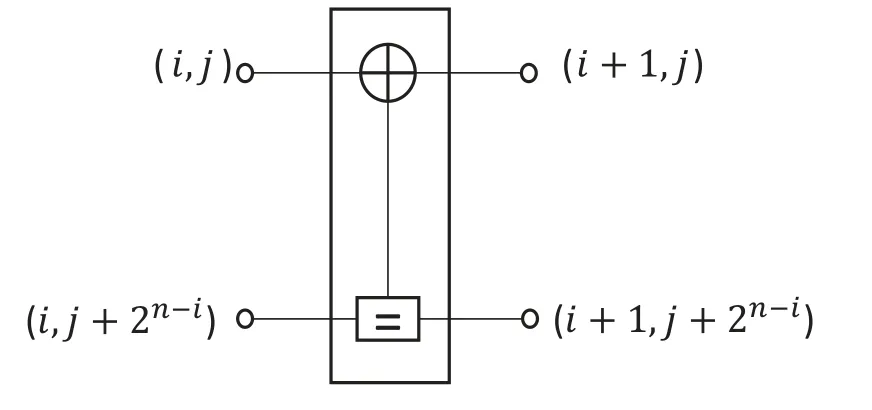
Figure 2.The basic processing element(PE)of BP decoder for a polar code.

wheretis the number of iterations.Ni=2n-i,n=logNandg(x,y)=ln((1 +xy)/(x+y)).g(x,y)could also be approximately equal tog(x,y)≈sign(x)×sign(y)×min(|x|,|y|) in hardware implementation.After the left-directed message is propagated to the left-most side,the right-directed message propagates to the right-most side,and then the likelihood information completes an iterated update.Finally,the decoder makes a hard decision at the leftmost nodes (1,j) to estimate the information bits when the terminated condition is satisfied.

The initial value of the right-directed messagecorresponds to whetherjis a frozen bit or an information bit.Whenjis a frozen bit,the value is set to infinite.In contrast,whenjis an information bit,the value is set to 0 since the receiver does not confirm whether the information bit is 0 or 1 at the beginning.

In addition,the initial value of the left-directed messageis the channel input information after soft demodulation,which can be expressed as

The BPL decoding algorithm is proposed for improving the performance of the BP decoding algorithm while simultaneously maintaining its parallel character.As mentioned in the above description,BP decoding is iteratively calculated in the factor graph,which is constructed on the basis of the generator matrix.Under this premise,different transposed matrices could be obtained by exchanging the columns in the generator matrix.Then according to these transposed matrices,different permuted factor graphs could also be obtained,as shown in the Figure 4.The BP List decoder consists ofLdifferent BP decoders on the basis of these permuted factor graphs.As shown in Figure 3,after selectingLpermuted factor graphs Π1...ΠL,the received soft information is calculated in these permuted factor graphs simultaneously.Then,all the obtained source sequences will be checked by the CRC code.If any sequence passes the CRC check,this sequence is output as a decode result.If all sequences fail to pass the CRC check,the codeword with the minimum code distance to the received sequence will be found as the output result.

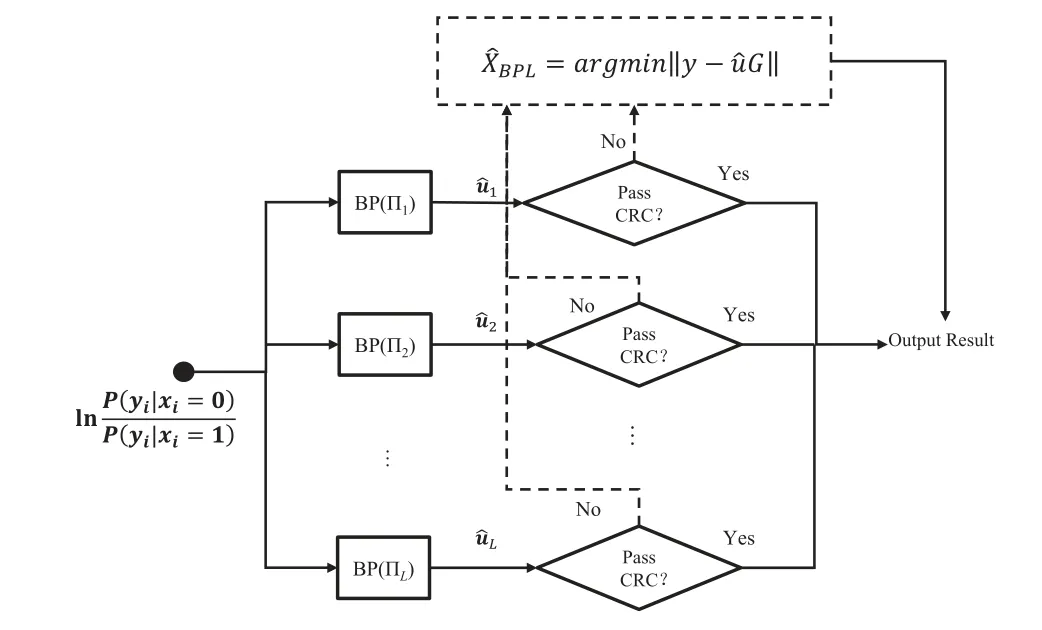
Figure 3.BP List decoding diagram using CRC check.

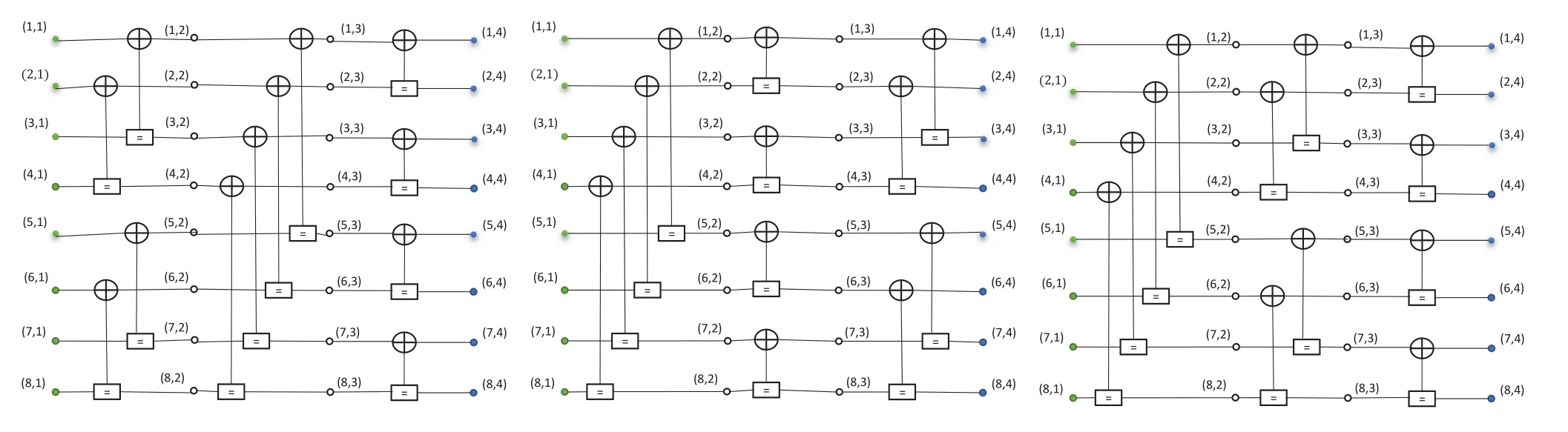
Figure 4.Different permuted factor graph for(8,4)polar code.

2.3 Bit-Flipping

For polar codes,the strategy of bit-flipping was first proposed to eliminate the error-propagation of SC decoding [5],which is called SCF decoding.The SCF decoding designs an FS with sizeωand implements an additionalTattempts at re-decoding.After that,many improved SCF decoding algorithms have been proposed to improve the accuracy of finding the first error bit [6].In particular,several algorithms with higher bit-flipping order have been proposed[25,26],which significantly improve the hit rate for the first error bit.Inspired by SCF decoding,initially,BPF decoding [27] was proposed by identifying the errorprone bits in the critical set similar to primitive SCF decoding.In contrast to SCF decoding,the BPF does not flip the first error bit directly,but assigns a priori LLR to +∞or-∞for a flipped bit.Since then,several improved BPF algorithms have been proposed to improve the error-correction performance of BP decoding [13,16].Furthermore,in the latest work,the strategy of bit-flipping is extended to SCAN decoding and obtained the performance gain [21].It motivates us to explore an appropriate scheme of bit-flipping to improve the performance of BPL decoding.

To identify more than one error,the GBPF-Ω decoding[16]procedure whose maximum bit-flipping order is Ω was proposed,and progress was achieved.The GBPF-Ω decoding procedure performs additional decoding attempts after GBPF-(Ω-1) decoding fails.Letϵω={i1,...,iω}denotes the indices of FS.During decoding,the bit with the index listed inϵωwith the smallest LLR magnitude needs to be flipped in turn.Then,if the estimated information bits do not pass the CRC,together with the flipped bit in the last attempt,another bit whose index is also listed inϵωwith the smallest LLR magnitude will be flipped again.The flipping procedure is briefly illustrated in Figure 5.

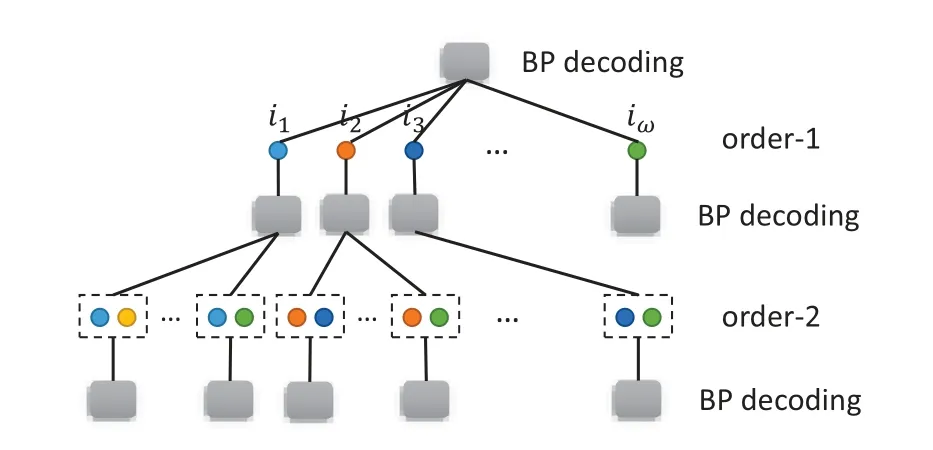
Figure 5.The procedure of GBPF-2 decoding.

As challenges exist with respect to the required memory and computational complexity,the GBPF-Ω decoding only studied the condition of Ω=2 in the literature [16].It can be easily determined from Figure 5 that,after the operation of bit-flipping,the BP decoding attempt will be performed in turn.Therefore,the additional BP decoding attempt will increase substantially if the size of FS is large enough.This will result in higher latency and may even offset the advantage of parallelism of BP decoding.For this reason,we propose the segmented bit-flipping scheme for BPL decoding,to balance the needs of computational complexity and improved performance.

III.THE ERROR DISTRIBUTION AND FLIPPING SET

In this section,the error distribution of information bits with BPL decoding is shown when the SNR is 2 dB and the number of iteration is 200.The code length N is 1024,the number of information bits is 544,which is equal toK+C.HereKis the number of original information bits that is not added to the CRC code andCis the total number of the redundancy check after the CRC encoded.Figure 6(a)shows the error-distribution of information bits,and Figure 6(b)shows an example of segmentation for information bits.The frozen bits are selected by the Monte Carlo method,a heuristic simulation based construction for specific decoding algorithm[28,29].

From Figure 6(a),it is not difficult to determine that the error-distribution of BPL decoding is different from that of serial decodings such as the SC or SCL algorithm,and even BP decoding,for which the difference is also apparent.Errors are more likely to occur in the second half of the entire length.Moreover,unlike the SCAN decoding,the most error-prone bit is not located in the first half,but in the second half of the code.Therefore,for the information bits located within the first half of the entire length,their errorprobabilities are much lower than those of the second half.In line with this feature,for BPL decoding,we focus the segments on the second half.The first half can be a separate sub-block.

Figure 6(b)also illustrates the generation of FS and the segmentation method.It is well known that the FS should consists of the most unreliableωbits under BPL decoding.Hence,we choose the information bits with the highest error probabilities as the elements in FS.In other words,the FS is generated by the error-probabilities of information bits.For example,for (1024,544) polar code,it can be determined from the Figure 6(a) that,the information bits whose error probability is greater than 0.25 are selected in the FS.Meanwhile,the segmentation is also pursued.Figure 6(b)shows an example in which the FS is constructed and divided into several sub-blocks.

Assuming that the construction method for the polar code is the Monte Carlo method,the evaluation of error probability for each bitPican be obtained.Note that here the density evolution or Gaussian approximation(GA)[30]could also be applied,but their evaluation is not as accurate as the Monte Carlo method.After selecting the frozen bits,the remainder are the information bits.Then,normalization to the information bits is carried out by,wherePmaxis the highest error probability of the information bits.The bits with the conditionPei ＞ψare selected in FS,whereψis a threshold value;ifψis set larger,the size of FS is smaller.Meanwhile,the FS will be divided into several segments in terms ofPei.For example,as shown in Figure 6,the FS is divided into four segments A,B,C and D,and CRC bits are included.Note that the error probability for each component is decreased in turn.Then,the remaining information bits in the second half will be uniformly divided into three segments,and the CRC bits will also be added.This method of segmentation takes advantage of the parallel characteristics of BPL decoding;for the first time,a complete segmentation of the FS has been realized.

Next,we will discuss the length of segments in the FS.Generally,the FS is split intomsub-blocks by CRC.In each sub-block,Ibis represented as the original capacity of a sub-block from bit-channels in FS,andis the expectation ofIb.The higher value of the expectation,means the more opportunities to be decoded correctly for the sub-block[31].Hereis denoted as

Proposition 1.If there is pe1＞pe2＞···＞pet ＞···＞ pem,to makePe(N,M,F1,F2,...,Fm)assmall as possible,it must be established that l1＜l2＜···＜lt ＜···＜lm,where l1+l2+···+lm=M.

according to the setting condition,there ispe1＞pe2.Now we first assume thatl1＞l2.Sincel1+l2=M,thenl1＞M/2 andl2＜M/2.Lettingl1-M/2=a,(7)could be formulated as:

Similarly,ifl1＜l2,lettingl2-M/2=a,(7)could be formulated as:

Hence,according to Proposition 1,if we divide the FS into several segments,we will note that the length of the segment increases as its error-probability decreases.

IV.HIGHER-ORDER SBPL-BF DECODING

As an enhanced BP decoding algorithm,the performance gain of BPL decoding is still limited at the cost of multiple space complexities.In particular,after adding the CRC code,compared with CA-SCL decoding,the gap in performance is not negligible.Hence,to further improve the error-correction performance of the BPL algorithm with the concatenated CRC code,an improved BPL decoding algorithm based on segmented bit-flipping is proposed in this paper.In contrast to most BPF algorithms which only process the priori LLR for those erroneous decoded bits,the proposed algorithm not only handles the erroneous decoded bits but also involves the correct decoded bits to speed up convergence.

4.1 The Principle for Segmentation

The proposed BPL decoding takes advantage of the cooperative property of each BP decoder in the original BPL decoding.In theLoutput sequences of BP decoders,there are different positions at which the erroneously decoded bits are located.As shown in Figure 7,it is assume that the decoding errors occurred in theS2andS4sub-blocks of the BP decoder Π2and these two sub-blocks do not pass the CRC check.Meanwhile,theS2andS4sub-blocks in other decoders have passed the CRC check,and the output result ofS2andS4in the BP decoder Π2can be modified through the two same sub-blocks of other decoders.In the same way,we can also modify the output result of sub-blockS5in the BP decoder ΠL.Finally,the priori LLR about these correctly decoded bits of sub-blocks is processed.It is well known that the higher the reliability of priori information,the better convergence of the iterative decoding.Hence,this processing method could ensure maximized convergence in iterative decoding.It should be noted that the location selection of CRC is discussed in several literatures of serial decodings[32,33].However,as a parallel decoding,the decision bits of each decoder in BPL decoding is output simultaneously.Thus,for the sake of simplicity,here onlyc-bits cyclic redundancy check is appended to the information bits in each sub-block.

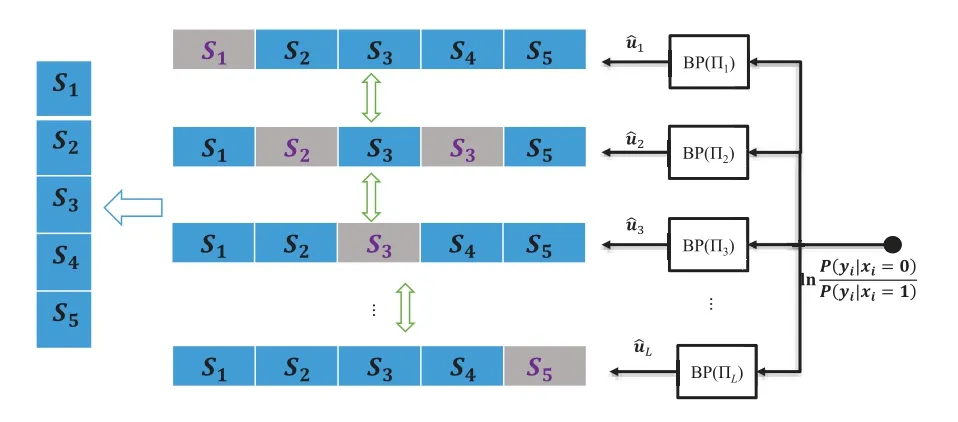
Figure 7.The segmentation principle in BP List decoding.

4.2 The Processing of Prioiri Information

Figure 8 shows the relationship between the error probabilities and the sorted index of a segment in the FS.When the decision result of these information bits fails to pass the CRC check,the information bits will be sorted by descending order according to their corresponding absolute LLR value.The horizontal axis of Figure 8 is the sorted index,and the vertical axis is their corresponding average error-probability.From Figure 8,it can be seen that the larger sorted index,the higher error-probability.Hence,the processing formula is designed in this work for the priori LLR of information bits in the erroneous segments:

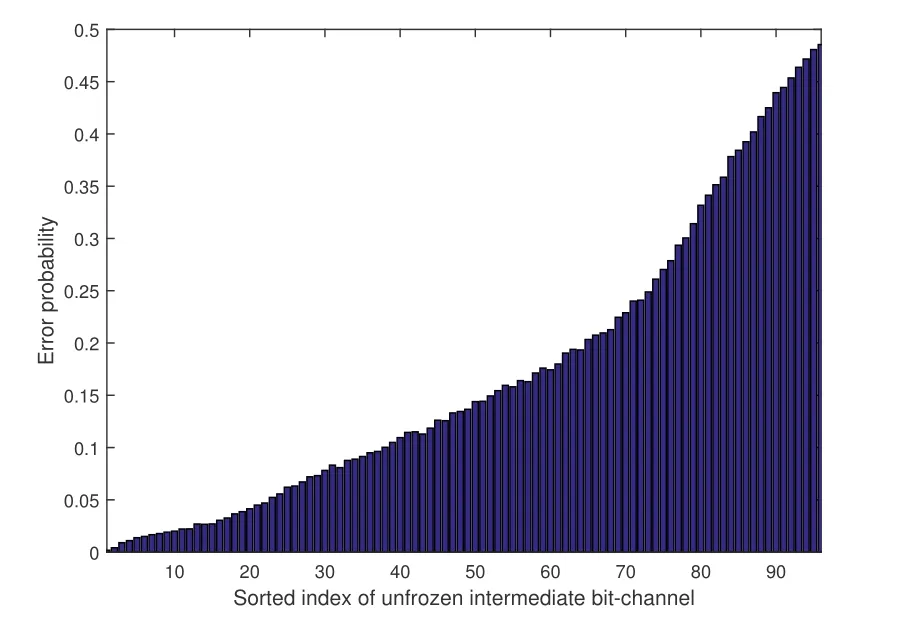
Figure 8.The relationship between the sorted information bits and their error probabilities.

whereorderis the sorted index (by its LLR magnitude),andC′is a constant,usually corresponding to the length of the segment.The purpose of designing this formula is,the more reliable the bit in the erroneous sub-block is,the higher the magnitude of a priori LLR,and vice versa.In this way,compared with directly using the threshold as the criterion for rightdirected message processing [34],the designed processing method is more dynamic and flexible.In particular,when the bit-flipping order Ω≥3,the computational complexity is too high to execute the decoding process.Hence,formula(13)provides a feasible solution for the proposed SBPL-BF decoding,which can be clarified in the next subsection.

4.3 Implementation of High Order SBPL-BF Decoding

The procedure of the proposed SBPL-BF decoding is intuitively similar to the GBPF-2 decoding [16].Compared with GBPF decoding,which operates bitflipping with only one or two bits in an additional decoding attempt,the proposed SBPL-BF is able to operate bit-flipping with multiple bits in an additional decoding attempt since dividing the FS into several segments.Figure 6 shows that the FS is divided into segments A,B,C and D according to their errordistribution.Assuming that all these sub-blocks failed to pass the CRC check,then the operation with one bitflipping will be carried out.Here each decoder could choose four bits (one bit in each segment) to do the bit-flipping attempt.It can be found from Figure 9 that the BP1 decoder,can select biti1in segment A,bitij-1in segment B,bitik-1∈Cin segment C and bitiω-1∈Din segment D and perform the decoding attempt at the same time.Likewise,the BP2 decoder can select biti2in segment A,bitijin segment B,bitik∈Cin segment C and bitiω∈Din segment D simultaneously.If the attempt with one bit-flipping does not pass the CRC,the operation with flipping of two bits will be performed.In a similar way,two bits in each segment will be selected,and each BP decoder could choose total eight bits to do the bit-flipping attempt.Therefore,compared with GBPF-2 decoding,the proposed SBPL-BF decoding significantly reduces the additional decoding attempts.The maximum additional decoding attempt number decreased fromTωin GBPF toTωin SBPL-BF,whereLis the number of BP decoders.

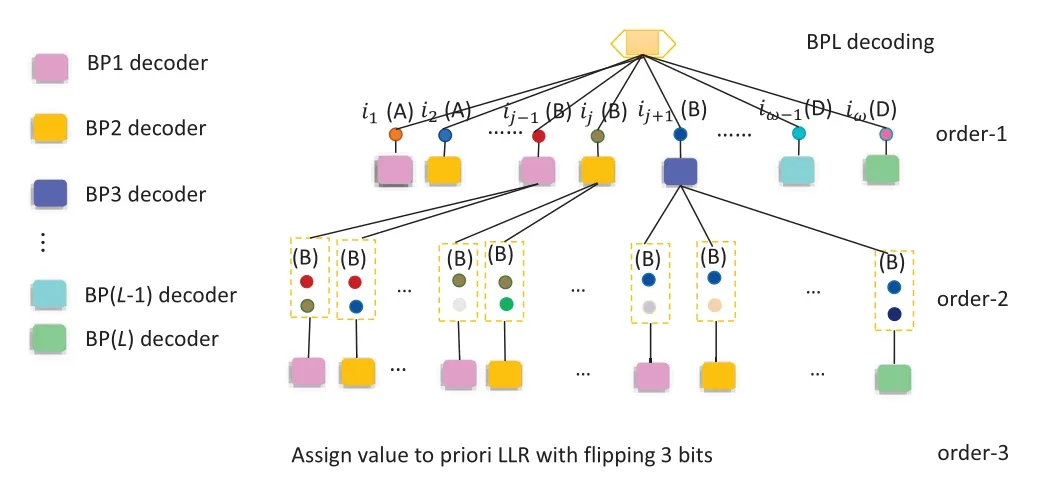
Figure 9.The procedure of SBPL-BF decoding.

Algorithms 1,2 show the detailed process of the SBPL-BF algorithm,wheremis the number of partitions(Line 6 in Algorithm 1),andR0,sis the vector used to store the priori LLR of the information bits in thes-th segment.If information bits of thes-th segmentˆu0,sare considered correctly decoded,their priori information will be strengthened(Line 8 in Algorithm 1).Meanwhile,if the information bits of thes-th segment in FS do not pass the CRC check in all BP decoders,the indexswill be sent toSf(Line 10 in Algorithm 1),meaning that the segments are needed to perform the bit-flipping operation.Vsis the set of bit-flipping indices(Line 17 in Algorithm 1)in thesth segment andVi,sis thei-th element ofVs,stores the priori LLR of theVi,s-th bit that needs to perform the bit-flipping operation in decoderl(Line 19 in Algorithm 1).After the BPL decoding is complete,there areLvectors for output soft information of unfrozen bits since BPL decoding consists ofLBP decoders.Then,the soft information of codeword,which chooses the smallest Hamming distance between the estimated codeword and the received signal,L,is selected as the final output LLR of information bits,andLsis the output LLR of thes-th segment inL.In this way,the selectedLshas a higher reliability.Note that for the segments that do not pass CRC check,each segment selects theLbits with the smallest absolute LLR value fromLsfor the bit-flipping operation (Line 17 in Algorithm 1).Hereτis a finite value.After the additional decoding attempt with bit-flipping order 1,if more than one segment fails to pass the CRC check,we will updateSfto(Lines 25-31 in Algorithm 1)and prepare the flipping attempt with order 2.Because the flipping attempt with order 2 is operated on the basis of order 1,the size ofis less or equal thanSf(∈Sf).For the flipping attempt with order 2,is the remaining part ofLstaking away theLsmallest absolute LLR values,and the indices of theLsmallest absolute LLR values inwill be sent to the setV ′s(Line 3 in Algorithm 2).andstore priori information of theVi,s-th and-th unfrozen bits that need to perform the bit-flipping operation in thes-th segment of decoderl,respectively(Line 9 in Algorithm 2).Moreover,after every BPL decoding has been finished,for all of the segments that pass through the CRC check to each BP decoder,the priori LLR of these information bits will be frozen to the correct value (Lines 20-21 in Algorithm 2).This reflects the utilization of the cooperative property of each BP decoder.Then,for those segments that failed pass the CRC check,the processing of priori information in previous Subsection 4.2 will be executed,wherelsis the length of thes-th segment(Lines 31-35 in Algorithm 2).Note that the sign of priori information of 3 bits with the smallest absolute LLR values will be flipped in a reverse direction (Lines 32-33 in Algorithm 2),and the other’s priori information will be enhanced as their signs remained in a same direction with their bit signs(Line 35 in Algorithm 2).By the way,to the best of our knowledge,BPF decoding with bit-flipping order 1,requiresT1additional decoding attempts[16].In contrast,the proposed algorithm only needs one additional decoding attempt(Lines 15-22 in Algorithm 1)and effectively reduces the decoding latency.It is worth noting that H-matrix-aided BF decoding is proposed and used in this SBPL-BF decoding algorithm(Line 40 in Algorithm 2).H-matirxaided BF decoding will be described in the Section V.

4.4 Performance Bound of BPL-Genie Decoding

In addition,a BPL-Genie decoder is designed to analyze the performance bound of the BPL with bitflipping(BPLF)decoding.Similar to the BP decoding,BPL decoding is a parallel algorithm,in which all information bits are decoded simultaneously.If we only flip the first erroneous bit,it is not reasonable to analyze the performance bound because other erroneous bits are also caused by noise.These errors(including the first error) can be propagated in the FG together,which is why BPL decoding performance is affected.Therefore,the designed BPL-Genie decoding senses erroneous bit and freezes them to the correct value.Figure 10 shows the BLER performance of the BPLGenie decoder for (1024,512) polar codes.The performance of the oracle-assisted BP with flipping order 1(OA-BP-1)[16]and the exhaustive one code-bit correction(EOCC)[22]decoding is also exhibited for comparison.BPL-Genie obtains a 0.8 dB gain over BPL decoding and even outperforms CA-SCL decoding by 0.3 dB at BLER=10-4.Thus,flipping one bit correctly can yield significant performance improvement for BPL decoding.

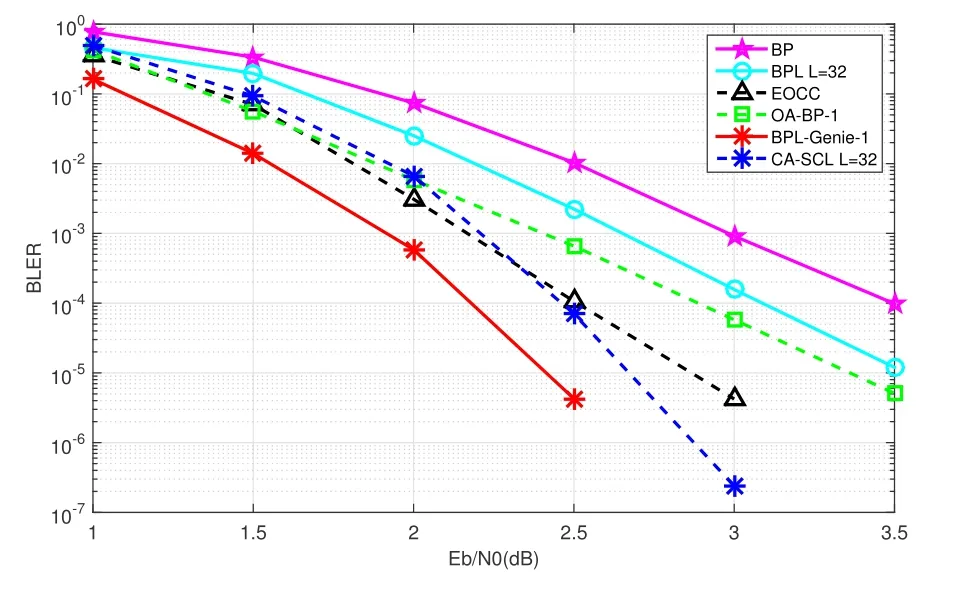
Figure 10.BLER performance of OA-BP-1, EOCC and BPL-Genie decoding for(1024,512)polar codes.

V.H-MATRIX-AIDED BIT-FLIPPING IN CODE BITS

The priori knowledge of code bits (on the channel side) has been a concern in recent years.As a representative of this,a BPC decoder is proposed to achieved great performance gain by correcting the prior knowledge of an erroneous code bit.However,all of these decodings still result in a visible performance gap with respect to CA-SCL decoding,especially whenLis large enough.Herein,we design an H-matrix-aided bit-flipping algorithm in code bits(HA-BFC)and merge this algorithm with the bitflipping operation of information bits in BPL decoding,which makes the proposed SBPL-BF decoding more competitive.The polar code parity check matrix H is first introduced in linear program(LP)decoding [35].The H-matrix is formed from the columns ofGwith the frozen bit indices.For example,the Hmatrix withN=8 and rateR=0.5 is

In short,bit-flipping in code bits,first estimates all the check equations in H and flips the selected bits in the decoded codeword.Here,we mainly estimate the reliability of the bit in the decoded codeword by using the syndromes=rHTand the decision-related LLR magnitude,whereris the estimated codeword.The posterior LLRYLLR=Ln+Rnis selected to estimate the received codeword,whereLnandRnare the left-directed message and right-directed message at the rightmost nodes,respectively.Mris the index set,where the index is the position of element 1 in ther-th row H-matrix,andNcis the index set,where the index is the position of element 1 in thec-th column of the H-matrix.i and j are the row index and column index in the H-matrix,respectively,where i∈Mrand j∈Nc.Then,the metric of reliability for an code bitψi,j=minj′∈Ncj|yj′| is denoted,and the metric of reliability for the estimated codeword is

It can be found that the first part ofEjcontains the reliability information for all the sums of syndromes that orthogonal to the j-th estimated bit and yet does not contain the information about the j-th bit itself.This part indicates the extent to which the bit should be flipped.Then,the second part provides the reliability information that the bit should be accepted,indicating the extent to which the bit should be maintained.Finally,the bits corresponding to theωlargestEjvalues are selected to form the flipping set.

The parameterρis a positive real number,called confidence coefficient,which is designed to optimize the reliability metric so that the decoding error rate is minimized.Obtaining the optimum ofρby theoretical analysis is difficult,the value ofρis usually obtained empirically by simulation.Figure 11 present the BLER performance of HA-BFC decoding for different values ofρ.As seen from this graph,whenρ=16,the BLER performance can be optimized.It is worth noting that BLER performance is not greatly affected by the different values ofρ.Thus,how the value of parameterρis ascertained does not determine the final performance of the algorithm.For simplicity,the value of this parameter is usually kept constant during the whole decoding process.

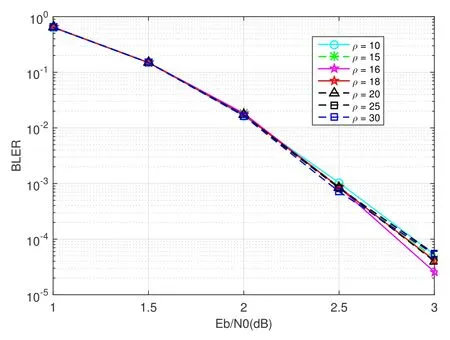
Figure 11.BLER performance of the different ρ in HA-BFC decoding.

Here,we apply the proposed HA-BFC to code bit flipping on the channel side.Figure 12 illustrates the BLER performance of HA-BFC decoding compared with conventional BP,SCAN,SCL decodings and state-of-the-art BPC decoding.As displayed in the figure,HA-BFC decoding improves the performance gain by 0.7 dB over the conventional BP decoding.In particular,whenω=64,the performance of HA-BFC decoding is the same as that of BPC decoding whenω=214.This means that HA-BFC decoding reduces the additional decoding attempts significantly for the same performance.

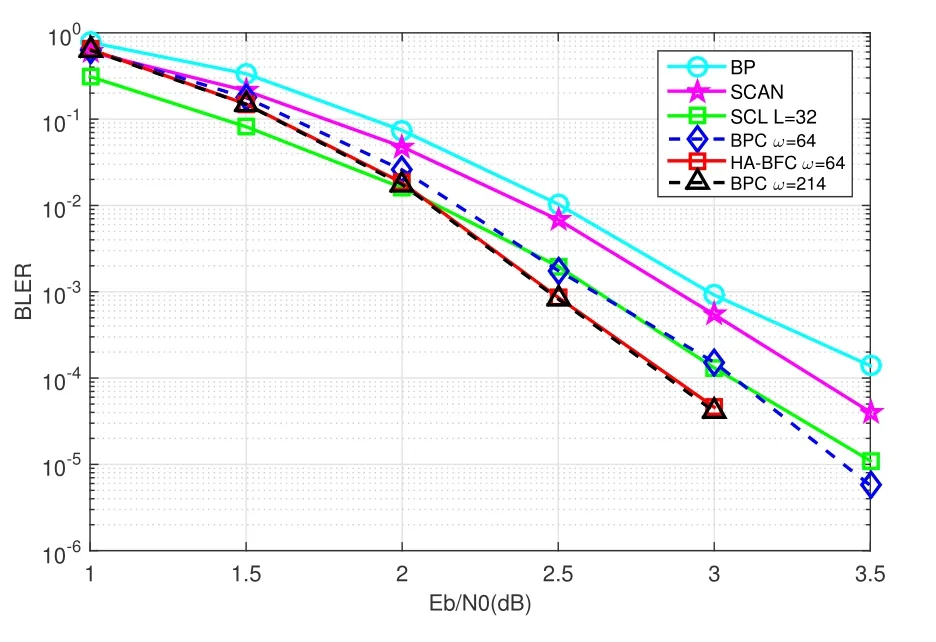
Figure 12.BLER performance of the HA-BFC compared with the BP,SCAN,SCL and BPC decodings. Imax is set to 60.

Furthermore,Algorithm 3 shows the detail of how HA-BFC is combined with SBPL-BF decoding.It is noted that HA-BFC is activated when SBPL-BF decoding begins the bit-flipping operation with order 3(Lines 1-14 in Algorithm 3).Assumingω=64 andL=32,due to the presence ofLBP decoders,only 2 bits need to be flipped in each BP decoder(Lines 18-20 in Algorithm 3).Therefore,compared with BPC decoding,Algorithm 3 also significantly reduces the decoding latency.

VI.SIMULATION RESULTS

In this section,the simulation results are shown for the performance comparison between the proposed algorithm and other decoding algorithms over the additive white Gaussian noise (AWGN) channel under different code lengths,and the modulation type is BPSK.The maximum number of iterations (MaxIter) is set to 200,which is the same as that of the original BPL decoding and its series of improvements[36,15,37].For a fair comparison,the construction method of polar codes for all decoding algorithms is based on the Monte Carlo method[28].First,we exhibit the performance comparison with the 1024 code length and the rate is 0.5.Here the number of segments is set to 8,and CRC-4 is chosen.For the sake of fairness,for all of the compared decoding algorithms that utilize the CRC aid,the length of CRC code is 32.In our proposed algorithm,both the number of uniform segments and the number of non-uniform segments(for the flipping set) are 4.The length of each segment A,B,C and D in FS is 22,36,50 and 64,respectively,while the length of the other uniform segment is 93.Hence,the rate of inner code is(512+32)/1024=0.53125,and the overall rate is 512/1024=0.5.

The performance comparison between the proposed decoding algorithm and other decoding algorithms is displayed in Figure 13.As shown in Figure 13,the proposed decoding algorithm is much better than the GBPF-MS decoding algorithm [16].In particular,it achieves a performance gain of approximately 0.25 dB at BLER=10-5compared with the novel post-processing method for belief propagation list(NPBPL)decoding[37],which is the state-of-theart improved BPL decoding algorithm.Meanwhile,the proposed algorithm also outperforms the CA-BPL decoding that the sum product decoding based on the CRC check matrix is selected.Note that We have added the experiment about the parity-checkconcatenated polar codes with BPL decoding (PCCBPL),for the sake of fairness,here the 32-bit paritycheck encoder is selected,and the scattered random construction is chosen the same as that of the literature[38].The result shows that the performance of the PCC-BPL is worse than the CRC-concatenated polar codes with BPL decoding.It means that the paritycheck is more suitable for the serial decodings.This could be explained as follows,a parity bit is decided by its parity function and it plays the role of error detection in a soft manner[38].That means if one bit in a parity function except the parity bit is wrong with a path,its parity bit is forced to be in error.Then,its subpaths tend to have lower path metrics and their probabilities of being pruned tend to increase.This helps to reduce elimination errors of an SCL decoder [39].Taking the SCL decoding as example,if there is more than one path pass a parity-check,these paths could all be kept for the candidate in the list of SCL decoding.Usually,the list contains a correct path and has a positive effect on the decoding process of next bits.However,as the decision bits of each decoder in BPL decoding is output simultaneously,there is no other path metric for selecting the correct path except the minimum code distance.Obviously,the selected correct path is not guaranteed by relying on the minimum code distance.Therefore,the CRC-concatenated polar codes is more suitable for parallel decodings.

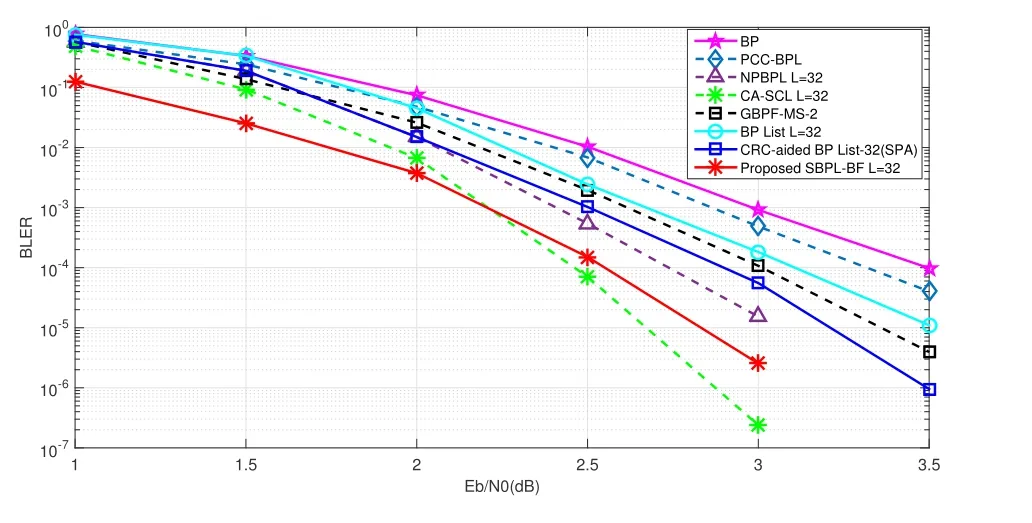
Figure 13.BLER performance of SBPL-BF decoding against BPL,GBPF,CA-BPL,NPBPL and CA-SCL decoding for(1024,512)polar codes.

Figure 14 shows the performance comparison of the proposed algorithm and the main polar code decoding algorithms.The code length is 2048 and the code rate is also 0.5.As shown in Figure 14,the proposed decoding algorithm is still better than the latest NPBPL and CA-BPL decoding algorithms.Figure 13 and Figure 14 show the error-correction performance of the proposed algorithm is better than that of CA-SCL decoding in the low SNR region,while at a higher SNR,the proposed algorithm is worse than CA-SCL decoding.There are two reasons to explain the latter result.On the one hand,CA-SCL decoding algorithm has a very low probability that the path of the correct codeword is outside the list at a higher SNR;on the other hand,limited by the check capability of the CRC-4 code,the situation may appear that all the subsequences could pass the CRC check at a higher SNR even if the codeword is incorrect,which incurs performance loss of the proposed algorithm at a higher SNR.However,it is well known that the excellent performance of CA-SCL decoding is obtained at the cost of high latency due to its serial nature.Comparatively,the proposed algorithm has an obvious advantage in latency due to its parallel nature.To evaluate the latency of SBPL-BF decoding,here,the clock cycleis adopted as the decoding latency metric.According to (1) in Section II,assuming the calculation in PE is carried out in a single clock cycle,we have=Imean·2 logN,whereImeanis the average number of iterations.Hence,for the sameN,the clock cycle is determined byImean.The curve ofImeanfor different SNR is shown in Figure 15.In Figure 15,it can be observed that when the SNR is low,the average number of iterations of the proposed algorithm surpass that of the other early termination rules[40].However,as the SNR increases,the average number of iterations rapidly decreases,which is better than the terminating criterion using the minimum absolute LLR value.Then,depending on the cycle count using the radix-2L sorter in[41]as well as theImeanobtained in Figure 15,Table 1 compares the average number of cycle clocks between the CA-SCL decoding and the proposed SBPL-BF algorithm.As shown in Table 1,the average number of clock cycles of the proposed algorithm is far less than that of the CA-SCL algorithm due to its parallel nature.Consequently,the proposed algorithm will be more attractive in practical applications.

Table 1.Comparison of average number of clock cycles between CA-SCL and SBPL-BF for different SNR.

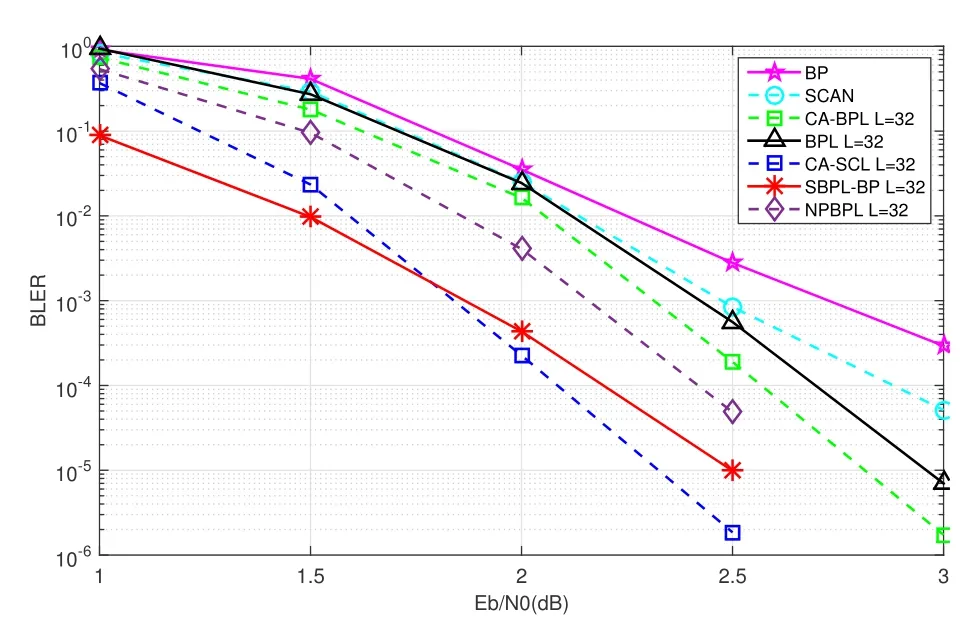
Figure 14.BLER performance of SBPL-BF decoding against SCAN, BPL, CABPL, NPBPL and CA-SCL decoding for(2048,1024)polar codes.

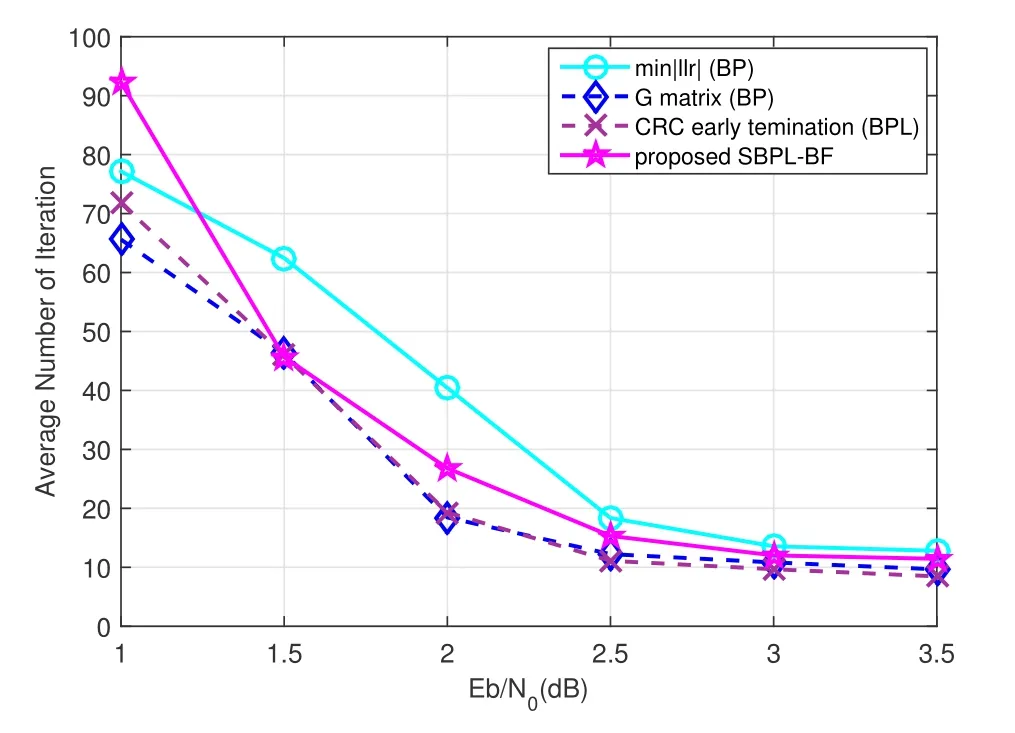
Figure 15.Average number of iterations for early BPL stopping criterion about(1024,512)polar codes.

Finally,the comparison of the decoding convergence is also demonstrated for different decoding algorithms.In Figure 16,it can be clearly seen that the convergence of the proposed algorithm is better than that of the other decoding algorithms.Particularly,when the number of iterations is 80,the proposed algorithm begins to converge,and two other improved BPL decodings still do not converge.This is attributed to the processing of those correctly estimated segments(the correct bits identified by the CRC check).

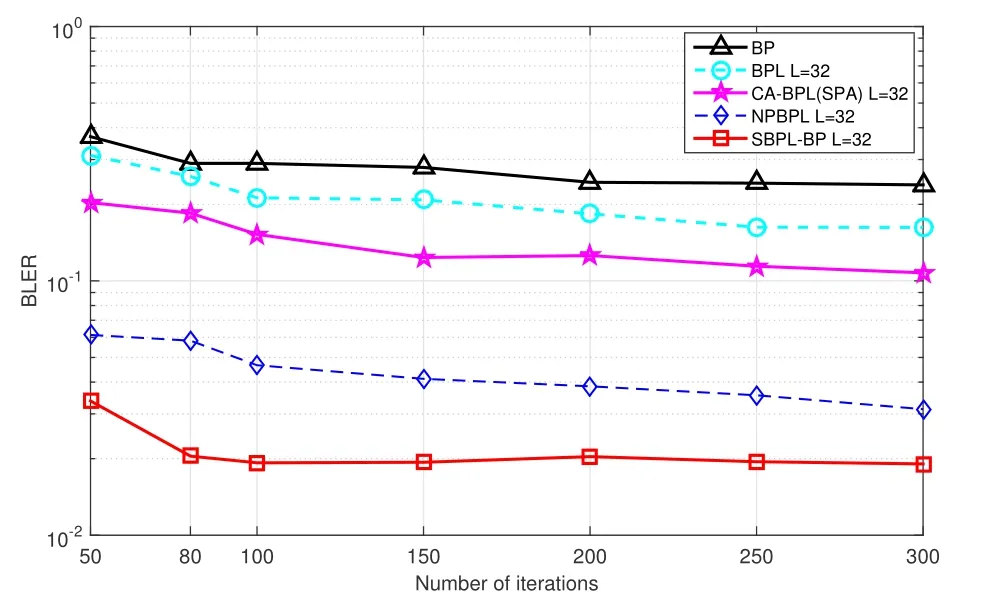
Figure 16.Convergence comparison in different decoding algorithms for(1024,0.5)polar codes at SNR=1.5dB.

VII.CONCLUSION

In this paper,a novel and improved segmented BPL decoding algorithm with bit-flipping is proposed.Based on the error-distribution,the flipping set is chosen and divided into several non-uniform segments.Then,combining uniform segmentation with non-uniform segmentation,a higher-order bit-flipping method for BPL decoding is proposed,and a flexible and effective method of assigning the priori LLR to the erroneous segment is designed.Furthermore,we design the HA-BFC algorithm for code-bits of the channel side and merge it with bit-flipping for unfrozen bits.The proposed SBPL-BF decoding exhibits better BLER performance and a shorter clock cycle than the state-of-the-art improved BPL and CA-SCL decodings,respectively.Meanwhile,the decoding convergence shows that SBPL-BF achieves better convergence than other improved BPL decodings.

ACKNOWLEDGEMENT

This work has been funded by the Key Project of NSFC-Guangdong Province Joint Program(Grant No.U2001204),the National Natural Science Foundation of China (Grant Nos.61873290 and 61972431),the Science and Technology Program of Guangzhou,China (Grant No.202002030470),and the Funding Project of Featured Major of Guangzhou Xinhua University(2021TZ002).