HetNets Under Decoupled Uplink and Downlink Access with UE Random Discontinuous Transmission: Local Delay and Energy Efficiency

Zhang Yue,Zheng Fuchun,Luo Jingjing

School of Electronic and Information Engineering,Harbin Institute of Technology(Shenzhen),Shenzhen 518055,China

Abstract: Due to the limited uplink capability in heterogeneous networks(HetNets),the decoupled uplink and downlink access(DUDA)mode has recently been proposed to improve the uplink performance.In this paper,the random discontinuous transmission (DTX)at user equipment(UE)is adopted to reduce the interference correlation across different time slots.By utilizing stochastic geometry,we analytically derive the mean local delay and energy efficiency(EE)of an uplink HetNet with UE random DTX scheme under the DUDA mode.These expressions are further approximated as closed forms under reasonable assumptions.Our results reveal that under the DUDA mode,there is an optimal EE with respect to mute probability under the finite local delay constraint.In addition,with the same finite mean local delay as under the coupled uplink and downlink access(CUDA)mode,the HetNets under the DUDA mode can achieve a higher EE with a lower mute probability.

Keywords: decoupled uplink and downlink access(DUDA);heterogeneous networks(HetNets);random discontinuous transmission(DTX);stochastic geometry

I.INTRODUCTION

With the rapid growth of global mobile data and increased demand for a better quality of service (QoS),the heterogeneous networks (HetNets),where multiple low-cost and low-power small base stations(SBSs)are deployed over the existing macro base stations tier(MBSs),have become a key architecture for the future communications networks [1,2].Recently,the importance of uplink (UL) performance in HetNets has arisen along with the development of social networking,UAV surveillance and cloud solutions [3].However,under the conventional coupled UL and downlink (DL) access (CUDA) mode,where both the UL and DL of a user are associated with the same BS,the UL performance may be limited by the DL parameters such as different transmission powers of the BSs in different tiers.Although several techniques under CUDA,e.g.,cell range extension(CRE)[4],have been proposed to mitigate the impact of inter-tier differences,the association criterion based on the best DL performance generally does not result in the best UL performance as well.Therefore,the concept of decoupled uplink and downlink access (DUDA) has been proposed in [5],which enables users or UEs to be connected with different BSs for their UL and DL.Under the DUDA mode,without affecting the DL association,a user is allowed to be associated with the BS which receives the strongest signal in the UL,thus ensuring a high-quality UL transmission.In [6],a UL performance comparison was carried out,showing that the DUDA mode leads to better load balance for HetNets and has a better or equal average spectral efficiency(SE)and energy efficiency(EE)than the CUDA mode.Based on DUDA,the impact of fractional power control(FPC)on the delay and EE of UL HetNets was investigated in [7],but the influence of the interference correlation was not considered.

Apart from SE and EE,local delay,defined as the average time taken until a data packet has been transmitted successfully,is a key component of transmission delay and is considered an important performance metric reflecting the QoS and network reliability [8].In [9],an approximation of the interfering user point process was used to derive the mean local delay in a single-tier uplink network.For a static low-mobility HetNet,the time correlation in the spatial distribution of the nodes will cause interference correlation between different time slots [10],resulting in an increase of local delay (i.e.,the same set of interfering users may be faced by a BS across different time slots).Particularly,the local delay may become an infinity for certain poor interferer distribution,referred to as network-contention phase transition [11].As such,[12] employed random discontinuous transmission (DTX) at BSs to reduce DL mean local delay.[13] investigated the local delay of DL HetNets with random DTX where user and BS locations are correlated.Inspired by this,we in this paper also adopt the UE random DTX scheme,by allowing UEs to be muted independently and randomly in each time slot,to weaken the interference correlation and reduce the local delay.

On the other hand,the uplink DTX scheme,in the context of the explosive growth of mobile smart devices,is also beneficial for saving energy consumption on the UE side [14].Yet the decrease in energy consumption may not imply a rise in energy efficiency(another key performance metric in this paper),since throughput is also affected by device sleeping.In contrast with the legacy cycle-based DTX or discontinuous reception (DRX) [15],the impact of UE random DTX on uplink energy efficiency remains to be studied.

In fact,the trade-off between the delay and EE is one of the important trade-off issues in HetNets and has been extensively investigated [16-18].The Het-Nets,especially DL HetNets with DTX at BSs,have been well analyzed.In [19],considering the random BS-DTX,the mean local delay and EE of DL HetNets based on the Poisson cluster process were analyzed.

However,the relationship between the mean local delay and EE in the UL HetNets with UE random DTX has not been adequately studied.On the one hand,due to the usual orthogonal access mode within each BS cell,only one UE per BS transmits on a particular resource block and forms interference only to the UE in other cells.The uplink interfering point process therefore is more difficult to model than downlink interference due to the correlation between the Voronoi cells of the Poisson-Voronoi tessellation and the channel access scheme in each cell[9].On the other hand,the analysis of downlink performance does not need to consider the direct impact of uplink parameters(as in most literature),whereas the uplink performance is directly subject to the downlink parameters such as downlink power.This is another motivation for the DUDA analysis in this paper.Furthermore,the respective impact of UE DTX on DUDA-based HetNets and the performance differences between DUDA and CUDA modes,have yet to be explored.In this paper,we therefore focus on a DUDA-based UL HetNet and investigate the impact of UE random DTX on the mean local delay and EE by comparing the performance of the DUDA and CUDA modes.The main contributions can be summarized as follows:

• Utilizing stochastic geometry,we derive thebth moments of the conditional successful transmission probability(STP)with UE random DTX,leading to general results for the mean local delay and EE in a UL DUDA-basedK-tier HetNet with UE random DTX.Furthermore,simplified expressions of the mean local delay and EE under the same cross-tier path loss exponent are obtained for DUDA and CUDA mode,respectively.

• Based on a reasonable assumption on the distribution of interfering users,we further obtain some approximation results with closed forms for local delay and energy efficiency in DUDA-based and CUDA-based HetNets,respectively.Then,the range of the signal-to-interference ratio(SIR)threshold that makes the local delay a finite value and the bounds of optimal SIR threshold that maximizes the energy efficiency are obtained.In addition,the effect of the mute probability is also analyzed.

• With the simulation results,we reveal the effect of the key parameters (e.g.,SIR and mute probability) on local delay and EE.Under the finite mean local delay constraint,the relationship between the maximum EE and the mute probability is investigated.Finally,the performance difference between the DUDA and CRE-based CUDA is also analyzed.

II.SYSTEM MODEL

2.1 Heterogeneous Network Model

We consider an uplink HetNet with DUDA comprisingKindependent tiers of BSs.DenotingK={1,...,K},for anyk ∈K,the positions of BSs in thekth tier follow a homogeneous Poisson point process (PPP) Φkwith intensityλk.Moreover,the BSs across tiers differ in terms of transmit powerPk.We assume that each BS schedules only one user on each resource block(RB)at a given time,i.e.,orthogonal access under the same BS is assumed.The user point process is also modeled as a homogeneous PPP Φuwith densityλuand independent across{Φk}k∈K.Note that the user density is assumed to be sufficiently high such that there is always at least one interfering user served by another BS.All users have the same transmit powerPu.Furthermore,the standard path loss model with the path loss exponents{αk}k∈K ＞2 for tierkis used.Letht,xdenote the power fading coefficient between the user atxand the tpical user’s serving BS(termed tagged BS)at the origino ∈R2in time slott.We assume that{ht,x}are spatially independent over the different links,temporally independent across time slots,and follow the exponential distribution with unit mean (i.e.,the Rayleigh fading model).In addition,since the interfering user density is typically high in an ultra-dense HetNet,we ignore the noise and focus on the interference-limited regime.

In this paper,we focus on the uplink transmission performance of the DUDA mode versus the CUDA mode.A simple case of transmissions in the DUDA and CUDA modes is depicted in Figure 1.In the conventional CUDA mode based on cell range extension(CRE),each user is connected to the same BS for both UL and DL transmissions,i.e.,the BS which offers the maximum long-term averaged biased received-power(BRP)in DL transmission.In the DUDA mode,however,the UL association can be different from the DL association.Each user accesses the BS which receives the strongest long-term averaged signal (transmitted by this user)in UL transmission,and therefore obtains the strongest uplink signal strength.DenoteDkas the association distance between a UE and its serving BS.According to[20,Lemma 3],when the biased transmit power ratio is equal to 1,the probability density function(pdf)ofDkin the DUDA mode can be expressed as

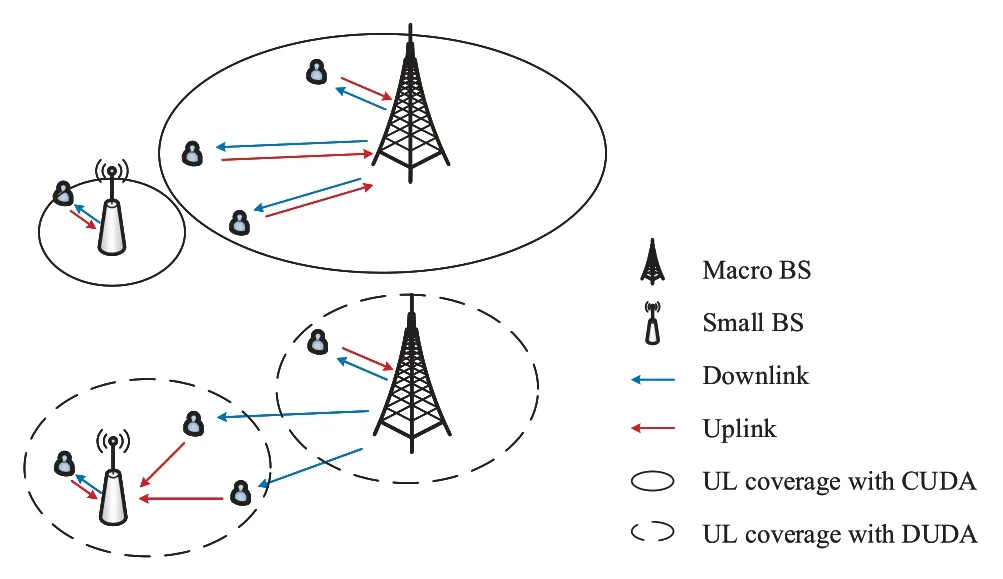
Figure 1.Illustration of CUDA and DUDA in a two-tier HetNet.

whereAkis the probability that a UE is associated with thekth tier BS in the DUDA mode [20],which is given by

2.2 UE Random Discontinuous Transmission Scheme

We assume that the time is divided into equal slots and each transmission attempt requires one time slot.In the random DTX scheme,each UE is in either of the two transmission states for each time slot,i.e.,the mute state and the active state.We model the transmission state in each time slot as a Bernoulli trial with a tunable parameterζ(0≤ζ ＜1)called mute probability.Namely,a UE in each time slot stays mute temporally independently with probabilityζand stays active with probability 1-ζ.

Denoting ΦI,j ⊂ΦuandIt,j,respectively,as the set of interfering users associated with thejth tier and their aggregate interference at the tagged BS in the time slott,then the overall interference at the tagged BS in the time slottis

where1(·)is the indicator function,Φu,tdenotes the set of active UEs in the time slott,andxj,idenotes the location of theith interfering user connected within tierj.The received SIR at the tagged BS in thekth tier and time slottis therefore

wherexk,0is the location of the typical user andRkdenotes the distance between the typical user under consideration and its serving BS at the tierk(i.e.,the tagged BS).

2.3 Performance Metrics

In this paper,we consider two performance metrics:the mean local delay and energy efficiency.

Mean Local Delay:We assume that retransmission will occur if a transmission fails in a certain time slot.The mean local delay is the mean number of transmission attempts(or time slots)needed before the first success if the transmitter is allowed to keep transmitting.

We consider the event that the received uplink SIR at the tagged BS in thekth tier is higher than a specific valueθ(i.e.the SINR threshold)in a time slot as a successful transmission event,which is denoted byCk|ΦIand conditioned on the distanceRkand the set of interfering users ΦI=∪j∈KΦI,j.The corresponding probability averaged over fading is termed conditional successful transmission probability(STP)and is given by

Given the point process,the needed number of time slotsLk|ΦIuntil a successful transmission is geometrically distributed with Pr(Ck|ΦI),thus the conditional mean ofLk|ΦIis Pr-1(Ck|ΦI).Therefore,the mean local delay in thekth tier can be obtained by the expectation with respect toRkand ΦI,i.e.,

From the law of total probability,the mean local delay of a HetNet can be expressed as

Energy Efficiency:We define the uplink energy efficiency(with the unit of nats/J/Hz)as the ratio of uplink area spectrum efficiency to average area user power consumption.Assuming that a fixed-rate transmission scheme is applied,i.e.,data packets are transmitted at the rate of log(1+θ)nat/sec/Hz in each time slot,the uplink spectrum efficiency can then be expressed by

Furthermore,the total power consumption of a UE in this paper is modeled as

wherePcandPsdenote the circuit power expenditure in the active state and mute state,ρis the UE power amplifier (PA) efficiency.Therefore,the energy efficiency can be calculated by

From (6) and (9),it can be observed that the mean local delay and the STP of a tier respectively are the-1-st moment and the 1-st moment of the conditional STP.In the next section,we will derive theb-th moment of the conditional STP,thus obtaining the expressions for the mean local delay and EE of aK-tier Het-Net with UE random DTX.

III.MEAN LOCAL DELAY AND ENERGY EFFICIENCY

Here,under the UE random DTX,we first analyze theb-th moment of the conditional STP in thekth tier(i.e.,then derive the general result of the mean local delay and EE in a HetNet under DUDA and further give some simpler expressions for a special case.

3.1 General Case and Main Results

Theorem 1.In a K-tier HetNet in DUDA mode with a UL random DTX scheme,the b-th moment of the conditional STP in the k-th tier is given by

Proof.The conditional STP in thekth tier can be evaluated as

where(a)and(b)follow the fact thatandare exponentially distributed with unit mean.Due to the uplink orthogonal access within each cell,only one UE per cell transmits on a resource block and there is no intra-BS or intra-cell interference.Therefore,ΦI,jis a non-stationary process with the intensity depending on the interfering distance[9],and the exact statistics of the interference are hard to derive.In this paper,we adopt the following approximation for the intensity function of ΦI,jaccording to[9],which is

where(a)is obtained by utilizing the probability generating functional(PGFL)of the general PPP[21]andfRk(r) follows (1).Then by employing the substitutiont=x2/r2we can obtain(12).

3.2 Special Case and Results

The expression of the mean local delay and EE can be simplified when the links in each tier are assumed to have the same path loss exponent,i.e.,{αk}k∈K=α.Note that under this assumption a UE will access the geographically closest BS in UL transmission when the DUDA mode is adopted.Then we have the results in the following corollary.

Corollary 1.When {αk}k∈K=α,the uplink mean local delay and EE of a K-tier HetNet in DUDA modewith UE random DTX are given by

In addition,based on a similar analytical procedure,we can obtain the same analysis to obtain the mean local delay and energy efficiency of the CRE-based Het-Net with CUDA according to [20,Lemma 3],which are given by(18)and(19).

Bjdenotes the bias factor of thejth tier,and=Bj/Bk,=Pj/Pk.

It can be seen from (18) and (19) that the performance of CUDA mode under=1 will be equivalent to that of DUDA mode.This is because,under such a condition,the BS selection in the UL will not be decided based on the difference of transmission power of BSs in different tiers-the BS is chosen according to the closest distance in the UL transmission,which ensures the strongest uplink signal strength.

3.3 Approximate Analytical Expressions

Since the equations(16)-(19)still contain complex integration terms,it is hard to directly obtain useful conclusions about the effects of network parameters on local delay and energy efficiency.Therefore,in this part,based on a reasonable assumption,we are to obtain some approximate closed-form equations of the analytical results and give some insightful propositions based on them.

For further simplification,we approximate the interfering users as following a homogeneous PPP distribution.Since the users further away from the tagged base station receive little influence from the tagged BS when choosing cells,their locations can be regarded as independent from the tagged BS.Therefore,it is reasonable to consider the interfering users as a homogeneous PPP distribution outside a certain range centered around the tagged BS.Moreover,in the area close to the tagged BS,the assumption may exaggerate the density of interfering users due to orthogonal intra-cell access,thus the results obtained based on this assumption will be slightly more pessimistic than the real situation (hence they can serve as a bound).As such,the interference density of users in thej-th tier is assumed to beλj.We then have the following conclusions.

Corollary 2.The mean local delay of DUDA-based and CRE-based CUDA HetNets can be approximated,respectively,as

Proof.For the DUDA mode,based on our assumption,the local delay in(16)can be rewritten as

It is worth noting that since(BjPj)2/α ＞1,we can conclude thatDC≥DD,where the equality holds taken when=1 forj ∈K.

The analytical results of (16) and (20) are given in Figure 2,and it can be seen that they have similar trends,with(20)performing slightly worse than(16),which confirms our previous analysis.It can also be seen that they converge to infinity at a certain SIR threshold,which we term the critical thresholdθc:

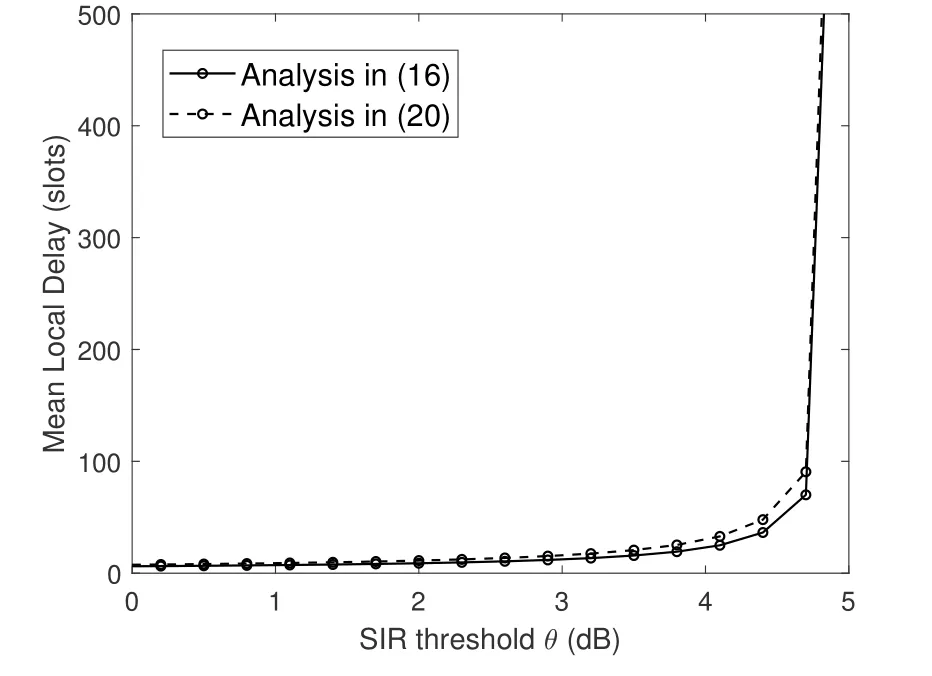
Figure 2.The analytical results of local delay for α=4 dB,ζ=0.7.

Determining the value of the critical thresholdθcis essential to allow the network to achieve a finite mean local delay,thus next we give the upper bound(i.e.,θc)on the value ofθthat enables local delay to maintain a finite value in DUDA and CUDA modes,respectively.

Proposition 1.In DUDA mode and CRE-based CUDA mode,the mean local delay is finite when the SIR thresholds θ satisfy

for CRE-based CUDA,respectively.

Sinceα ＞2,θcis an increasing function with respect toζ,illustrating thatθccan be increased by setting a larger mute probability,which leads to a lower mean local delay in the severe interference scenarios.

Utilizing a similar analytical approach,we can also obtain the approximations for EE.

Corollary 3.The energy efficiency of DUDA-based and CRE-based CUDA HetNets can be approximated,respectively,as

Similarly,it can be observed that≥since (BjPj)2/α ＞1.It also can be seen that both log(1+θ) andψ(θ,α) are increasing functions with respect toθ,and log(1+θ) has a larger slope whenθis small and gradually decreases and eventually falls below the slope ofψ.Therefore,there should be an optimal valueθ*for energy efficiency,i.e.,the solution for

For the DUDA-based HetNets,we give the approximate range of the value ofθ*below.

Proposition 2.In DUDA-based HetNets,the bounds of the optimal SIR threshold θ*that maximizes energy efficiency are given as

where γ=α2sin(2π/α)(2π(1-ζ))-1.

Proof.The derivative of(26)with respect toθyields

Sinceθ/(1 +θ) ≤log(1+θ) ≤θ,we have the following result

Then we can obtain the bounds ofθ*in(29).

It can be seen that the upper and lower bounds ofθ*are both decreasing functions ofζ,i.e.,asζincreases,the optimal valueθ*taking interval will move positively along the coordinate axis,which is not conducive to taking a finite local delay,so there is a tradeoff between local delay and energy efficiency.

IV.SIMULATION RESULTS

In this section,we present some numerical and simulation results to investigate the effect of the critical network parameters (i.e.,the SIR thresholdθand mute probabilityζ) on the mean local delay and energy efficiency.Moreover,some comprehensive comparisons of the performance for the DUDA mode and CRE-based CUDA mode are also provided.Here,we consider an interference-limited two-tier HetNet composed of MBSs (Tier 1) and SBSs (Tier 2) withα1=α2=α,and the system parameters are chosen according to[6],i.e.,P1=43 dBm,P2=21 dBm,Pu=10 dBm,Pc=Ps=13 dBm,ρ=1,λ1=1/（π5002）,λ2=5λ1andλu=200λ1.In addition,we perform the Monte Carlo simulations for a circular area with a radius of 1 km,and the results are obtained from an average of 10,000 independent realizations.

4.1 Effect of SIR Threshold

Figure 3 shows the mean local delay and EE as a function of the SIR thresholdsθwith different values of the UE mute probabilityζ.First,in Figure 3(a),the mean local delayDincreases withθ,and when the SIR threshold exceeds a critical valueθc(ζ),a phase transition occurs(i.e.,the mean local delay becomes infinite from being finite).Namely,due to the interference correlation in different time slots,consecutive unsuccessful transmission events are more likely to appear at a highθ(i.e.,high-rate regime).Moreover,it is observed thatθc(ζ)increases asζincreases.The reason is that the interference correlation is further reduced by the higher mute probability,and the finite mean local delay therefore can be achieved at a high SIR threshold.However,the mean local delay increases withζwhenθis low (i.e.,a low-rate regime whereθ →0),which means that the mean local delay is mainly influenced by the active state of the typical user rather than interference at a low thresholdθ.In addition,whenζ=0.7,Dhas a better performance in the DUDA mode compared to the CUDA mode with a 15 dB factor.On the one hand,the advantage of DUDA mode over CUDA is more obvious as the SIR threshold increases,e.g.,atθ=-1 dB,the former has a 2 dB advantage over the latter.On the other hand,it can be seen that DUDA mode has a higherθc(ζ),which means that users can transmit at a higher rate with a guaranteed finite mean local delay in DUDA mode.

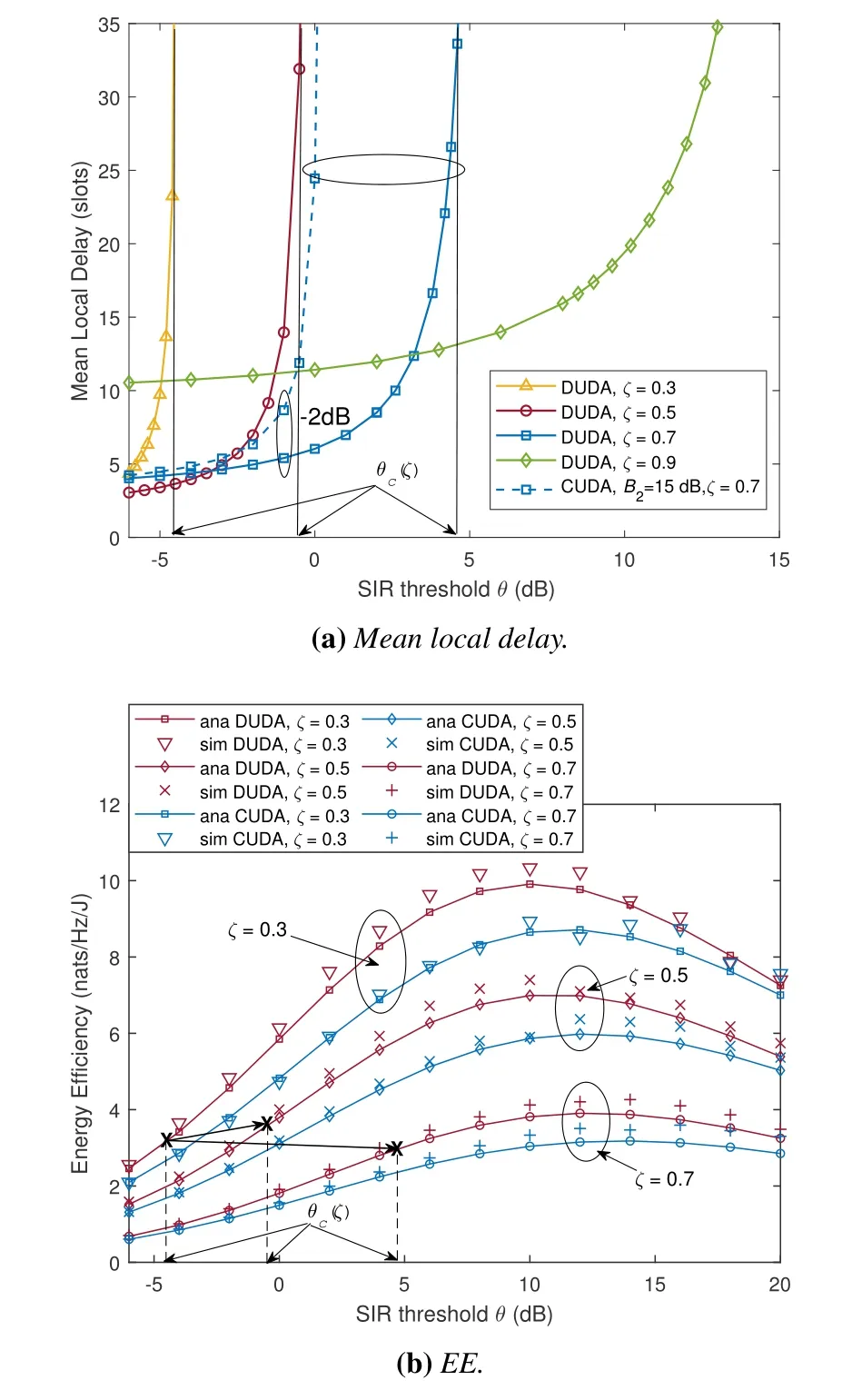
Figure 3.The mean local delay and EE as a function of θ,where α=4.

In Figure 3(b),the analytical (ana) and simulation(sim)results of EE are shown and their gaps lie within a tolerable range,and the reason for the existence of gaps is mainly due to the approximation of the interference intensity in (14).It is observed that for differentζand association rules,there exist optimal SIR thresholds making the energy efficiency optimal as a result of the combined effect of the transmission rate log(1+θ)and the STP.We also observe that DUDA mode has a higher EE compared to CUDA mode for the sameζ,because it can be ensured in DUDA mode that the connected BS can receive the strongest signal,while it cannot be achieved under CUDA whenP2B21according to(19).In addition,the energy efficiency decreases due to the decrease in throughput caused by the increase in the mute probabilityζ.So there exists a trade-off between reducing the mean local delay (or increasing the critical SIR thresholdθc(ζ)) and improving the EE.Here,however,we focus on the impact ofζon the maximum EE under the restriction of finite mean local delay since it is meaningless to discuss the performance of EE at the infinite local delay (i.e.,the message cannot be transmitted successfully).As can be seen from Figure 3(a),in the DUDA mode,whenζchanges from 0.3 to 0.5 and 0.7,the correspondingθc(ζ)increases,but the corresponding maximum EEηEE(θc) in Figure 3(b) slightly increases and decreases respectively.Clearly,there is an optimalζbetween 0.3 and 0.7 that optimizesηEE(θc)under the constraint of the finite mean local delay.(i.e.,increasingζdoes not always reduce the maximum EE at the finiteD).Moreover,the mild changes inηEE(θc) also show that the maximum EE may be achieved with an nearly stable level by increasing theθ(or transmission rate)when a higherζis adopted to increaseθc(ζ).

4.2 Effect of Mute Probability

Figure 4 shows the mean local delay and EE as a function of the mute probabilityζ.In Figure 4(a),first,for different values of SIR thresholdθ,there exists an optimal mute probabilityζoptthat minimizes the mean local delay in DUDA mode or CUDA mode,and it can be observed thatζoptand the corresponding optimal mean local delay increase with the increase inθ.Whenζ ＜ζopt,random DTX can decrease the mean local delay by reducing the interference correlation.Whenζ ＞ζopt,however,increasing the mute probability reduces the number of time slots that a typical user is active,i.e.,fewer transmissions are performed,which in turn increases the mean local delay.As theθincreases and tends to infinity,the probability of unsuccessful transmission also rises,then a higherζwill be needed to reduce the interference correlation (i.e.,ζopt →1).In addition,by comparing with CRE-based CUDA mode at the same SIR threshold,DUDA only needs a lowerζto have a lower bound ofD,which is certainly beneficial to achieving higher EE,as is also demonstrated in the following energy efficiency curves.

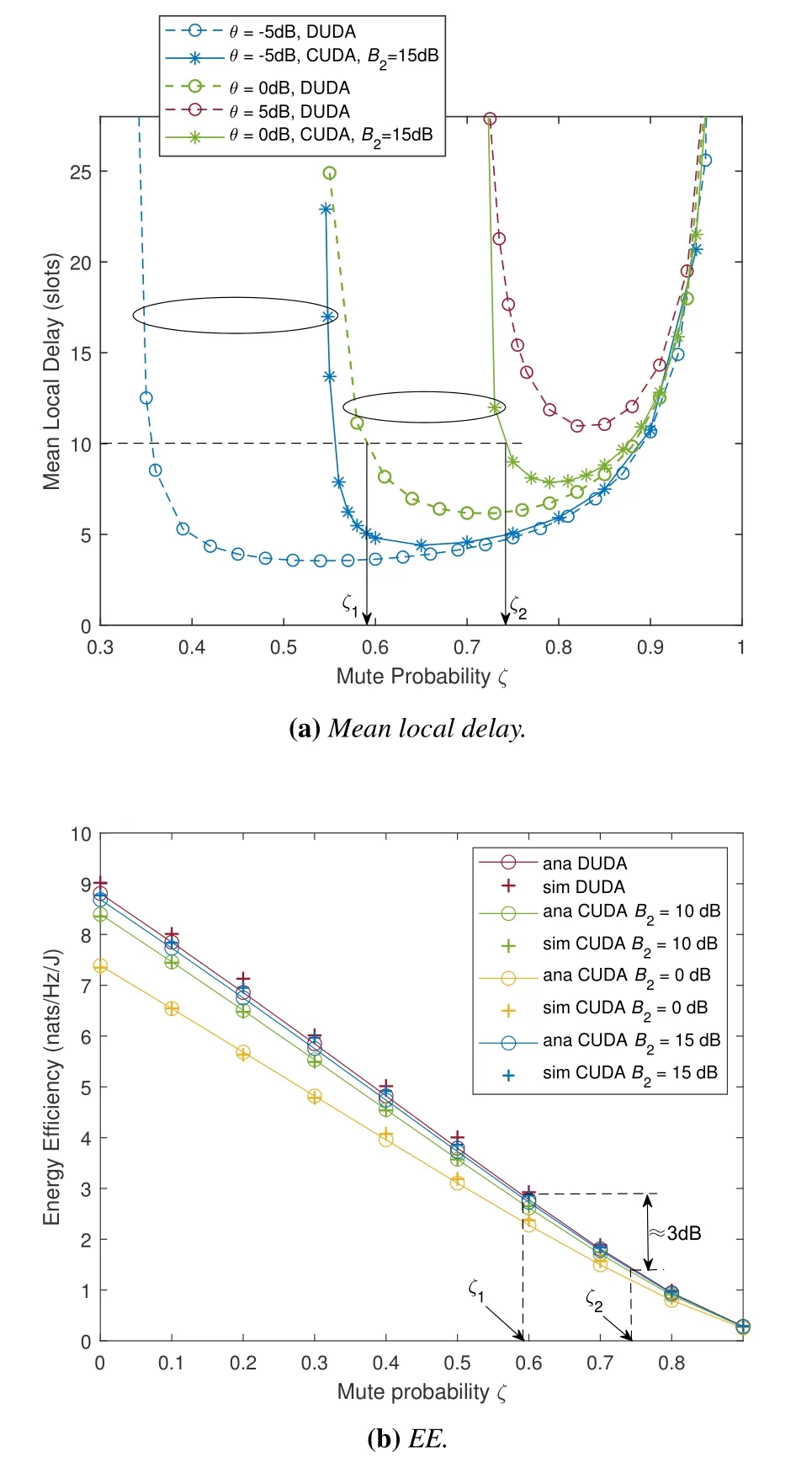
Figure 4.The mean local delay and EE as a function of ζ,where α=4.

In Figure 4(b),we also give analytical and simulation curves of energy efficiency with respect to the mute probability atθ=0 dB,and they can be matched well.Like our previous analysis in Figure 3,the EE degrades due to the mute probability increase that reduces the throughput of the system.We show the performance of EE in DUDA mode compared to the performance in CUDA mode based on different bias factors.It can be seen that the bias factor does have the ability to improve EE due to its ability to attenuate the effect of transmit power differences between different tiers of BSs and to balance the network load.As the bias factor increases (i.e.,P2B2/P1→1),it gets closer to the performance of DUDA.Furthermore,we compare the maximum EE that can be achieved with the same finite local delay in the DUDA and CUDA modes.WhenD=10 time slots in Figure 4(a),we first obtain the lower corresponding mute probabilityζ1in DUDA mode andζ2in 15 dB bias-based CUDA mode,respectively.Next,however,as can be seen in Figure 4(b),ζ1corresponds to an EE with a significant advantage of 3 dB relative toζ2.This shows that for the sameθ(or transmission rate),the DUDA mode,compared to CUDA mode,can achieve the same mean local delay but significantly higher energy efficiency with a lower mute probability.

V.CONCLUSION

First,we have analytically derived the mean local delay and energy efficiency of an uplinkK-tier HetNet with UE random DTX scheme in DUDA mode via the derivation of theb-th moments of the conditional STP.Furthermore,based on a reasonable assumption for interfering users,the simplified expressions with closed forms for the mean local delay and EE in the DUDA HetNet and the CRE-based CUDA HetNet were obtained,respectively.The analysis,along with the simulation results,provides some insight into the impact of the SIR threshold and mute probability on the mean local delay and energy efficiency.The simulation results revealed that in the DUDA mode,a finite mean local delay can be achieved via the random DTX scheme at the high SIR threshold,and the maximum EE is not always sacrificed by mute probability under the constraint of the finite local delay.In addition,comparing the performance of DUDA Het-Net and CRE-based CUDA HetNet,it has been found that the DUDA HetNet has a lower lower-bound of the mean local delay and a higher upper-bound of EE under a certain mute probability.With the same finite mean local delay as in CUDA mode,the HetNet in DUDA mode can achieve a significantly higher EE with a smaller mute probability.Further works will include clustered user distribution and overall HetNet performance with time division duplexing.

ACKNOWLEDGEMENT

This work was supported in part by the National Key R&D Program of China under Grant 2021YFB 2900304 and the Shenzhen Science and Technology Program under Grants KQTD20190929172545139 and ZDSYS20210623091808025.