Stackelberg Game for Wireless Powered and Backscattering Enabled Sensor Networks

Lyu Bin ,Cao Yi ,Wang Shuai ,Guo Haiyan ,Hao Chengyao

1 Key Laboratory of Ministry of Education in Broadband Wireless Communication and Sensor Network Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2 Jiangsu Engineering Research Center of Novel Optical Fiber Technology and Communication Network,Suzhou 215006,China

3 Guangdong-Hong Kong-Macao Joint Laboratory of Human-Machine Intelligence-Synergy Systems,Shenzhen Institute of Advanced Technology,Chinese Academy of Sciences,Shenzhen 518055,China

Abstract: This paper investigates a wireless powered and backscattering enabled sensor network based on the non-linear energy harvesting model,where the power beacon (PB) delivers energy signals to wireless sensors to enable their passive backscattering and active transmission to the access point (AP).We propose an efficient time scheduling scheme for network performance enhancement,based on which each sensor can always harvest energy from the PB over the entire block except its time slots allocated for passive and active information delivery.Considering the PB and wireless sensors are from two selfish service providers,we use the Stackelberg game to model the energy interaction among them.To address the non-convexity of the leader-level problem,we propose to decompose the original problem into two subproblems and solve them iteratively in an alternating manner.Specifically,the successive convex approximation,semi-definite relaxation(SDR)and variable substitution techniques are applied to find a nearoptimal solution.To evaluate the performance loss caused by the interaction between two providers,we further investigate the social welfare maximization problem.Numerical results demonstrate that compared to the benchmark schemes,the proposed scheme can achieve up to 35.4%and 38.7%utility gain for the leader and the follower,respectively.

Keywords: backscatter communication;energy interaction;stackelberg game;wireless powered sensor network

I.INTRODUCTION

The development of Internet of Things (IoT) enables the ubiquitous deployment of wireless sensor networks (WSNs),which have been widely used for environmental monitoring,logistics tracking,intelligent transportation,etc [1].However,a main bottleneck for applying WSNs is that the lifetime of WSNs is generally limited since wireless sensors are typically powered by their embedded batteries.The traditional methods to deal with this bottleneck are recharging or rechanging the batteries manually.However,the cost is usually unacceptable since the number of wireless sensors may be numerous.

Wireless power transfer (WPT) has been emerging as a promising way to recharge energy-constrained sensors wirelessly [2,3].This opens a network paradigm for self-sustainable WSNs,i.e.,wireless powered sensor networks(WPSNs),in which wireless sensors equipped with energy harvesting(EH)circuits can collect sufficient energy based on their demands[4,5].However,there are still some challenges for WPSNs needed to be addressed for their extensive applications.Specifically,a dedicated time slot for the EH is unavoidable based on the harvest-then-transmit(HTT)protocol[5],which limits the duration of wireless sensors’ active information transmission and results in an unsatisfying performance for WPSNs.

Backscatter communication (BackCom),an efficient technique for WSNs,can enable wireless sensors to passively deliver information by riding over the incident signals without the usage of active RF components[6].Thus,the dedicated EH time slot is not necessary for the BackCom.Inspired by this,the integration of BackCom and WPSN,i.e.,wireless powered and backscattering enabled sensor network(WPBSN),has been widely investigated in the literature[7-9].In a typical WPBSN,the power beacon(PB)is generally set to be selfless to supply sufficient energy to wireless sensors without considering its own cost.However,this assumption is actually not realistic due to the fact that the PB and wireless sensors may belong to different service providers,which prefer striving for their own benefits [10].For example,the PB may refuse to provide energy services if it does not satisfy with the benefits obtained from wireless sensors.Thus,it is worth investigating the energy trading process between the PB and wireless sensors in WPBSNs.

1.1 Related Works

Recently,WPSNs have received a great deal of attention [5,11-15].In [5],the authors first proposed the well-known HTT protocol,based on which wireless sensors first collect energy from the power beacon (PB) and then deliver information to the access point (AP).In [11],the authors introduced a fullduplex WPSN,where the WPT and wireless information transmission (WIT) can be implemented at the same time so that the communication efficiency can be highly improved.In [12],the authors investigated the energy-efficiency maximization problem for WPSNs under the constraint of minimum system sum-rate and designed the optimal resource allocation scheme.Different from [12],in [13],the authors formulated a Markov decision process based energy maximization problem and proposed a modified Q-learning algorithm to allocate the network resource optimally.In[14],the authors studied a cognitive radio technology enabled WPSN,where a deep reinforcement learning algorithm was proposed to find the optimal resource allocation strategy.In [15],the authors proposed to apply the non-orthogonal multiple access(NOMA)in WPSNs for spectrum efficiency enhancement,where multiple wireless sensors deliver information to the AP simultaneously.However,due to the severe pathloss,it generally takes a long duration to harvest sufficient energy in WPSNs[5,11,12].Especially when the channel conditions are not favorable,the longer EH duration seriously reduces the allocated time for the active information transmission of wireless sensors.This leads to a problem that how to exploit the EH duration for simultaneous information transmission.

The WPBSN is a novel network paradigm which integrates BackCom with WPSN to make full use of the transmission block for information transmission[7].Specifically,wireless sensors in the WPBSN are equipped with both EH and backscatter circuits for supporting the active information transmission and passive information backscattering,respectively.In [8],the authors proposed a hybrid backscattering scheme for WPBSNs,based on which wireless sensors can switch the backscattering modes according to the primary channel condition.In[9],the authors exploited multiple antennas at both the PB and the AP in WPBSNs for performance enhancement,where the transmit and receive beamforming vectors are carefully designed.However,in[7-9],the energy interactions between the PB and wireless sensors are ignored under the impractical assumption that the PB is selfless.

In order to fill this gap,game theory[16]has considered as an efficient method to model the strategic interactions between the PB and wireless sensors.In[17],the authors proposed different energy trading models to study the energy trading between the PB and wireless sensors in WPSNs.In [18],the authors investigated the sensing-pricing-transmitting process in WPBSNs based on the Stackelberg game.In[19],the authors jointly maximized the network sum-rate and energy efficiency in WPBSNs by using the Stackelberg game based economic framework.

1.2 Motivations

Although the WPBSN has received a great deal of attention and effective efforts have been made to promote its development,the study of which is still at the early stage and several important issues have been overlooked in the literature.

First of all,how to model the EH process of wireless sensors is one of the most key issues for investigating the performance of WPBSNs.In the previous works[17-19],the linear EH process was considered,which is actually impractical as energy harvesters’non-linear characteristics cannot be captured.To address this issue,a two-piece EH model was used to approximate the saturation behavior [9,20,21].However,it is worth pointing out that the two-piece EH model is still a simplified EH model,which cannot indicate the non-linearity of RF energy conversion efficiency for different input power levels and results in a mismatch for performance optimization.To eliminate this gap,a non-linear EH model based on the logistic function was proposed in [22].However,to the best of our knowledge,no works have investigated a WPBSN with this practical non-linear EH model.

Secondly,the entire transmission block for the WPBSN was not fully exploited,which results in a performance loss.Specifically,in[7-9,17-19],wireless sensors can only harvest energy from the PB within a part duration of the entire transmission block,which significantly limits the benefits achieved by the service providers.Thus,more efficient time scheduling schemes should be proposed.

Thirdly,how to model the energy interactions in the WPBSN by taking into account the above two issues stated above has not been studied yet,which also motivates our work in this paper.

1.3 Contributions

In this paper,we investigate the Stackelberg game based energy trading in a WPBSN,where the PB and wireless sensors belong to different service providers for energy trading.Different from [17-19],we consider the practical non-linear EH model,which can accurately model the EH process and avoid the mismatch for performance optimization.Compared to[7-9,17-19],we propose an efficient time scheduling scheme,based on which when one sensor backscatters information passively or transmits information actively,the other sensors can simultaneously harvest energy from the PB.Moreover,we design the energy beamforming and resource allocation scheme for maximize their respective benefits.The main contributions of this paper are summarized as follows:

• We consider a Stackelberg game based framework to model the energy trading process in a WPBSN,in which there exist a WSN service provider and an energy service provider.For the WSN service provider(i.e.,leader)constituted by wireless sensors and the AP,wireless sensors buy energy from the energy service provider(i.e.,follower)for information delivery.Accordingly,the energy service provider constituted by the PB obtains monetary incentives for providing energy services.

• To capture the characteristic of wireless sensors’EH circuits accurately,we utilize the non-linear EH model for avoiding performance degradation.Moreover,we propose an efficient time scheduling scheme for performance enhancement.In particular,the transmission block is divided into a passive backscattering phase and an active transmission phase.In each phase,when one sensor passively backscatters or actively transmits information to the AP,the other sensors can harvest energy from the PB at the same time.Moreover,we propose to exploit multiple antennas at the PB and the AP for further performance enhancement.

• To maximize the leader’s utility function,we propose to jointly optimize the energy price,energy beamforming at the PB,network time scheduling,and transmit power at wireless sensors.As the formulated problem is non-convex,we propose an alternating optimization (AO) algorithm to solve it.Specifically,we first solve the sub-problem of energy price,energy beamforming and transmit power by applying the successive convex approximation(SCA)and semi-definite relaxation(SDR)techniques,and then prove the tightness of applying the SDR.Then,we apply the variable substitution to transform the other sub-problem of time scheduling and transmit power into a convex optimization problem,and solve it by using standard convex optimization techniques.The convergence and computational complexity analysis of the proposed algorithm is further analyzed.

• To evaluate the performance loss due to the selfishness of two service providers,we also investigate the social welfare maximization problem and solve it efficiently.Furthermore,numerical results are provided to evaluate the performance of our proposed scheme.Compared to the benchmark schemes,the proposed scheme can achieve up to 35.4%and 38.7%utility gain for the leader and follower,respectively.

1.4 Organization

The rest of this paper is organized as follows.Section II describes the system model.In Section III,the problem formulation and proposed solutions are presented.In Section IV,the social welfare maximization problem is investigated.Section V provides the numerical results for performance comparisons.The conclusion of this paper is summarized in Section VI.

II.SYSTEM MODEL

We consider a WPBSN as shown in Figure 1,in which there exists a PB,Kwireless-powered sensors (denoted byUk,k=1,...,K),and an AP.The PB and AP are equipped withLandNantennas,respectively,while each sensor is equipped with single antenna.The sensors are considered to be equipped with both EH and backscatter circuits[7],which is controlled by a controller for mode switching.Specifically,when the EH circuit is activated,wireless sensors can harvest energy for supporting the active information transmission mode.Otherwise,if wireless sensors switch to the backscatter circuit,they can passively backscatter the incident signal for information delivery.The PB is embedded with a stable energy source for transmitting dedicated signals to support two functions,i.e.,delivering wireless energy for the sensors’EH and serving as incident signals to enable the sensors’ information backscattering.In addition,the PB is equipped with a high computational capability which can implement computational tasks for the network [20].Due to the blockages,the direct transmission link between the PB and AP is unavailable[9].

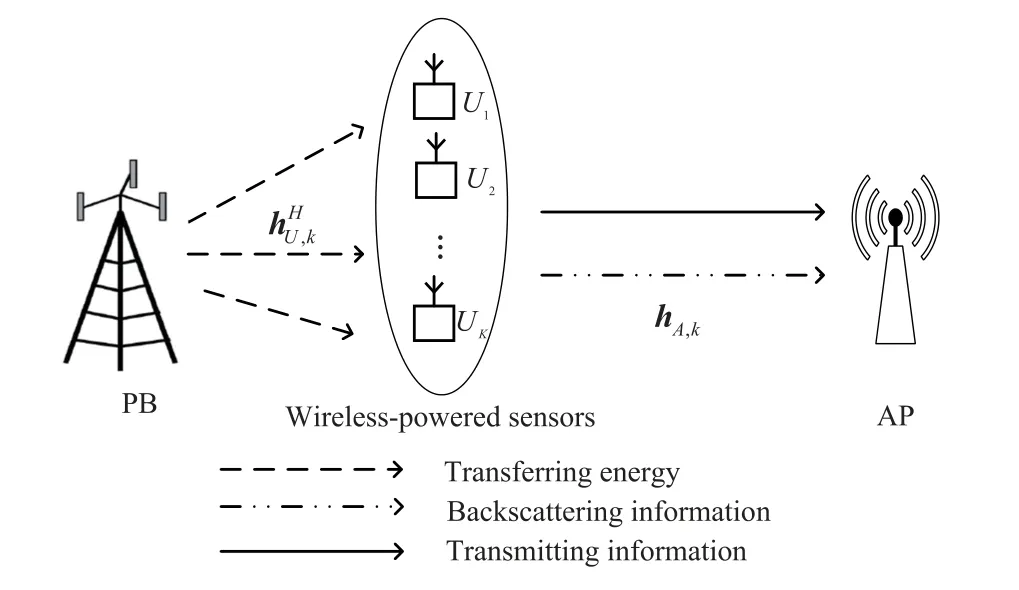
Figure 1.System model for a WPBSN.

We denote the links from the PB toUkand from theUkto the AP as∈C1×LandhA,k ∈CN×1,respectively,wherek ∈K,andK={1,...,K}denotes the set of wireless-powered sensors.We consider a quasi-static flat-fading channel model,based on which the channels remain stable in each channel coherence frame consisting of multiple transmission blocks.The channel state information can be efficiently obtained by using the pilot-based channel estimation methods.Without loss of generality,the normalized transmission block of interest,is divided into two phases,i.e.,the passive information backscattering phase and the active information transmission phase.In each phase,the information delivery for all sensors is scheduled via time division multiple access(TMDA) to avoid interference.As illustrated in Figure 2,the passive information backscattering and active information transmission phases are both divided intoKsub-slots,each of which is with duration ofτkandtk,respectively.

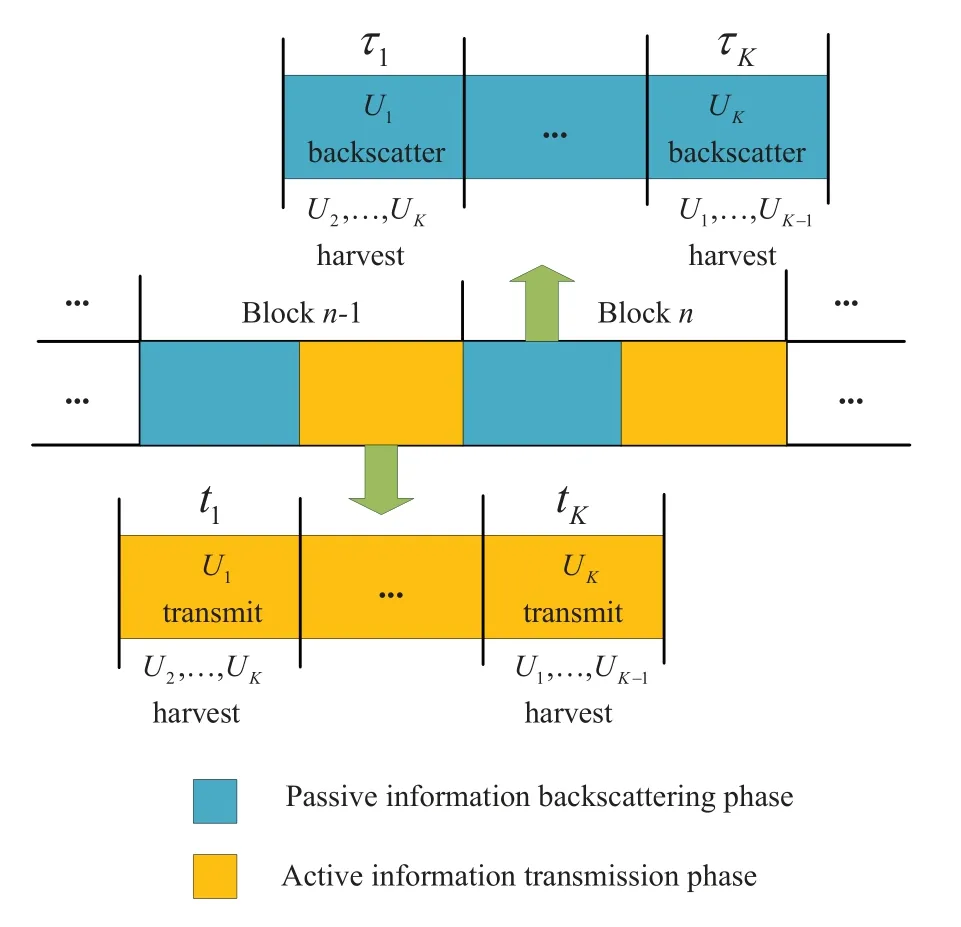
Figure 2.Time scheduling scheme for WPBSNs.

The PB transmits energy signals to all sensors over the entire transmission block.In the passive information backscattering phase,Ukdelivers information to the AP by backscattering the incident signal from the PB duringτk,and in the meanwhile the other sensors simultaneously harvest energy from the PB.Similarly,in the active information transmission phase,Ukactively transmits its information to the AP duringtkand harvests energy from the PB in the otherK-1 sub-slots.The total EH time forUkis thus given by 1-τk-tk.

2.1 Passive Information Backscattering Phase

In the passive information backscattering phase,the energy signal transmitted by the PB duringτj(j ∈K)is denoted byxP,j=wP,js,wheresis the prior known sequence with unit power,wP,j ∈ CL×1is the energy beamforming vector duringτjand satisfies||wP,j||2≤PP,andPPis the maximum transmit power at the PB.The received signal byUkfrom the PB duringτjcan be expressed as

wherenU,kis the antenna noise atUk.According to(1),the received RF power atUkduringτj,denoted byP1,k,j,is expressed as

Note that the noise power atUkis quite small for the EH and generally can be neglected [5,7,11,12].To capture the non-linear characteristics of the EH process,i.e.,the RF energy conversion efficiency for different input power levels,the practical non-linear EH model [22] is adopted.Then,the instantaneous harvested power atUkduringτjis given by

Duringτk,Ukmodulates its own informationckby riding overy1,k,k.The reflected signal byUkis thus expressed as

where 0≤βk ≤1 is the reflection efficiency atUk.The received signal at the AP fromUkduringτkis given by

in bps/Hz.

2.2 Active Information Transmission Phase

In the active information transmission phase,Ukcan still harvest energy from the PB.Denote the energy beamforming vector duringtkaswA,k,which satisfies||wA,k||2≤PP.Similar to the EH process in the passive backscattering phase,the total energy harvested byUkin the active transmission phase can be given by

Duringtk,Ukactively transmits its information by using the energy harvested in both passive backscattering and active transmission phases.It is known that there exist multiple adjacent blocks in a channel coherence frame[23].To guarantee the energy causality,Ukcan transmit information actively by using the energy harvested in the active information transmission phase of the (n-1)-th block and the passive information backscattering phase of then-th block,the illustration of which is shown in Figure 2.Denote the transmitted signal byUkaswherePA,kis the transmit power ofUk,andxU,kis the information-carrying signal with unit power.Due to the energy causality constraint,we have

wherePCrepresents the circuit power consumption of

Duringtk,the received signal by the AP fromUkis given by

The achievable rate ofUkduringtkis expressed as

In summary,the achievable network sum-rate is given by

III.PROBLEM FORMULATION AND PROPOSED SOLUTIONS

3.1 Problem Formulation

In this section,we consider there exists two service providers in the WPBSN.Specifically,the PB is from the energy service provider,which can provide the energy service,i.e.,the PB supplies energy to these wireless-powered sensors.The WSN service provider,including the sensors and the AP,has to pay for its received energy service.Both the service providers aim to maximize their respective benefits,the complex interaction processes for which are modeled as a Stackelberg game.

Under the assumption that there exist multiple energy service providers which compete for selling energy to the WSN service provider [10],we consider the WSN service provider as the leader.The leader aims for maximizing the utility function by determining the paid energy price,network time scheduling,energy beamforming at the PB,and transmit power at wireless sensors.The leader’s utility function is defined as the difference between the total benefit and the payment for buying energy,which is given by

whereurepresents the unit benefit of the achievable sum-rate,andλis the unit energy price of the energy service provider.The leader-level problem is then expressed as

whereτ=[τ1,τ2,...,τK],t=[t1,t2,...,tK],andPA=[PA,1,...,PA,K].

The energy service provider is the follower,which adjusts the value of its maximum transmit power at the PB according to the energy price offered by the leader.The follower also aims for maximizing its utility function,which is defined as the difference between the payment achieved by transmitting energy and the corresponding cost.In particular,the utility function of the follower is given by

whereF(PP)=+BPPrepresents the follower’s cost of transmitting energy to the leader per unit time,AandBare positive constants.Then,the followerlevel problem is given by

The Stackelberg game of the considered WPBSN is constituted byP1andP2.The process of obtaining the Stackelberg equilibrium(SE)is summarized as follows.The leader first releases an energy price and adjusts its strategies (i.e.,network time scheduling,the PB’s energy beamforming,wireless sensors’ transmit power)to maximize its utility function viaP1.Then,the follower chooses the value of maximum transmit power to maximize its utility function inP2according to the released energy price.Finally,the leader and follower can achieve the SE of the formulated game,which is defined as follows.

Definition 1.Denote the solutions toP1andP2as λ*andrespectively.The SE of the formulated Stackelberg game can be expressed as(λ*,)if the following conditions are satisfied

where λ ≥0and PP ≥0.

From Definition 1,we find that the equilibrium solution can be obtained by using the backward induction.In particular,we can first solveP2to obtain the maximum transmit power at the PB with a given energy price.Then,the solution toP1can be further obtained based on the follower’s reaction,i.e.,the value of maximum transmit power at the PB.

3.2 Solution to the Follower-Level Problem

For a given energy priceλ,it can be found thatP2is a convex optimization problem since its objective function is a quadratic function with respect toPPand its constraint is affine.The optimal solution toP2,denoted bycan be straightforwardly obtained by setting the first derivative of the objective function to be zero,i.e.,

ConsideringPP ≥0,can be expressed as

According to(18),we observe that if the energy priceλis not larger thanB,the PB will not transmit energy to the sensors because the follower cannot achieve any monetary incentive by providing energy to the leader.For this case,the PB will keep idle,and the leader also cannot work as the energy is unavailable.Thus,determining an appropriate energy price is important for maximizing the utility values of both the leader and the follower.

3.3 Solution to the Leader-Level Problem

Then,we proceed to solveP1withSince the variables are coupled in the objective function and constraints,it can be found thatP1is a non-convex optimization problem,which is hard to solve directly.Thus,we propose an efficient AO algorithm to solve it.Specifically,we divide the variables into two groups,i.e.,{wP,k,wA,k,PA,λ}and{τ,t,PA},and optimize them iteratively in an alternating manner.

3.3.1 Optimizing Energy Beamforming,Transmit Power and Energy Price

Given{τ,t},we first optimize{wP,k,wA,k,PA,λ}by solving the following problem:

From(19),we can derive the following inequality

Based onzf,k,j,the constraint C1 can be recast as

With the new constraints C7 and C8,P3can be reformulated as

Proof.Please refer to Appendix A.

From Proposition(1),we find that applying the SDR will not affect the optimal result.We can also observe that the PB always prefers transferring energy to a desired direction in each sub-slot to enhance the amount of harvested energy or the backscattering rates.In addition,the optimal solution indicates that the sensors will use all their harvested energy to actively transmit information to the AP in the active information transmission phase.

For the SCA technique applied inP3.2,obtained in ther-th iteration is used as the feasible point for the(r+1)-th iteration.By iteratively solvingP3.2,we can finally obtain a near-optimal solution ofP3.

3.3.2 Optimizing Network Time Scheduling

We continue to optimize{τ,t,PA}with the fixed{wP,k,wA,k,λ}.The optimization of{τ,t,PA}can be achieved by solving the following problem

IV.SOCIAL WELFARE MAXIMIZATION

As the WSN service provider and the energy service provider aim for maximizing their respective utility functions selfishly,there exists a performance loss in social welfare,which is defined as the total revenues achieved by the two service providers.In this section,we investigate the social welfare maximization for the sake of evaluating the efficiency of the achieved SE.The optimization problem is formulated as

wheree=[e1,...,eK].It is obvious thatP4.1is a convex optimization problem and can be solved by using the interior-point method.

3.3.3 Algorithm Summarization and Analysis

AsP5is a non-convex optimization problem,we propose to obtain the near-optimal solution by optimizing{wP,k,wA,k,PA,PP}and{τ,t,PA}in an alternating manner.

Similar toP3,we first optimize{wP,k,wA,k,PA,PP}by fixing{τ,t}and applying the SDR and SCA methods.By introducingWf,kandzf,k,j,P5can be reformulated as

It is observed thatP5.1is a convex optimization problem and can be thus solved by using the interior-point method.It is worth noting that the conclusion in Proposition 1 also holds forP5.1.

Then,by fixing{wP,k,wA,k,PP},we continue to optimize{τ,t,PA}inP4.1,which is a simplified form derived fromP5.The algorithm to solveP5is similar to Algorithm 1 and omitted here for simplicity.Similarity,the computational complexity of solvingP5isO

V.NUMERICAL RESULTS

In this section,we evaluate the performance of the proposed scheme by numerical simulations.Following[9,10,20],we consider a two-dimension coordinate system,where the coordinates of the PB and the AP are set at (0,0) and (xp,0),respectively.Wirelesspowered sensors are randomly deployed in a circular area centered at (xs,0) with a radius ofr,and the location ofUkis denoted by (xk,yk).According to [10,23],we model the large-scale path-loss asD(d)=c0(d/d0)-α,wherec0=(ζ/(4π))2represents the path-loss at the reference distanced0=1 m,ζis the wavelength with a carrier frequency of 750 MHz,αrepresents the path-loss exponent,anddrepresents the distance between two devices.The smallscale fading is modeled as the Rayleigh fading with circularly symmetric complex Gaussian random variables with zero mean and unit variance[10,23].According to [26],the parameters of the non-linear EH model are set as follows:ak=1500,bk=0.0022,andMk=24 mW.Similar to those in[10],the other parameters are summarized in Table 1.The following benchmark schemes are considered for performance comparisons.

Table 1.System parameters.

• BackCom scheme: Each sensor is only equipped with a BackCom circuit for backscattering information,and all variables are jointly optimized.

• HTT scheme: Each sensor is only equipped with an EH circuit for powering the active information transmission,and all variables are jointly optimized.

• Equal time scheme:The duration of each sub-slot in both phases is considered to be the same,i.e.,τk=tk=1/(2K),and the other variables are jointly optimized.

We first verify the convergence performance of Algorithm 1 in Figure 3.It can be observed that the proposed AO algorithm can reach the predefined threshold (i.e.,ϵ) after only 6 iterations,which confirms the convergence efficiency of the proposed algorithm.Moreover,from Figure 3,we find that the convergence of the proposed algorithm is independent of the number of antennas of the PB,which indicates its robustness to different parameter settings.

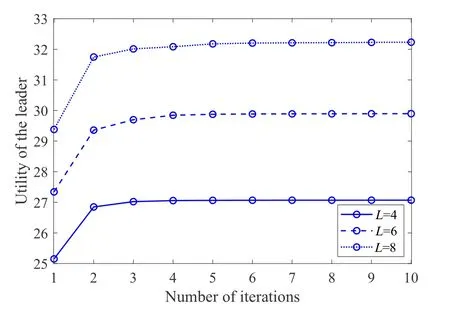
Figure 3.Convergence performance of Algorithm 1.

Figure 4 investigates the effect of the number of antennas at the PB on the utility of the leader.It is obvious that the utility functions of all schemes are increasing functions with respect to the number of antennas at the PB.The reason is that as the number of PB’s antennas increases,a higher antenna gain can be achieved,which thus enhances the energy transfer efficiency from the PB to wireless sensors and further improves the achievable sum-rate.In this situation,compared to the follower,the leader has more bargaining initiative and can negotiate its payment for buying energy with the follower for a higher utility value.As shown in Figure 4,the proposed scheme’s utility value is larger than that of the BackCom and HTT schemes.It is because compared to the BackCom scheme,when one sensor passively backscatters information to the AP,the other sensors in our proposed scheme can harvest energy from the PB for further information transmission.Compared to the HTT scheme,our proposed scheme can achieve the passive information delivery without using a dedicated time slot.Thus,our proposed scheme can achieve a larger utility value.In addition,we can observe that the social welfare scheme can always achieve the maximum utility value.The reason is that for the social welfare scheme,the leader and the follower aim to jointly maximize their total revenues,which avoids the performance loss suffered by selfishly maximizing the respective revenues of the leader and follower.

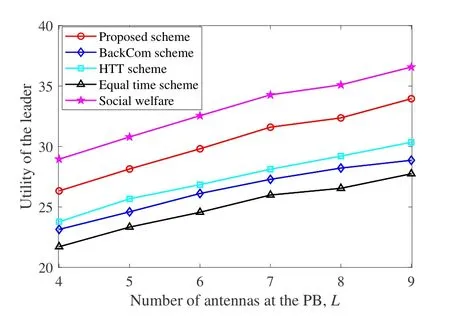
Figure 4.Utility of the leader versus L.

In Figure 5,we investigate the utility of the leader versus the distance between the PB and sensors.It is observed that asxsincreases within the range from 2 m to 5 m,the utility values of all schemes decrease.It is because the suffered attenuation determined by the cascaded channels,i.e.,the multiplication of the links from the PB to sensors and the links from sensors to the AP,is a non-decreasing function with respect toxsranging from 2 m to 5 m.It should be noted that whenxsis equal to 5 m,the utility value of the proposed scheme is the smallest.As seen from Figure 5,whenxsexceeds a threshold (e.g.,4 m),the performance of the HTT scheme is the worst.The reason is that when the sensors are far from the PB,the duration required for the EH becomes large and then the payment for buying energy increases.However,whenxsexceeds 5 m,the utility value of the leader in the proposed scheme will increase a little bit since the attenuation condition of the cascaded channels becomes better.

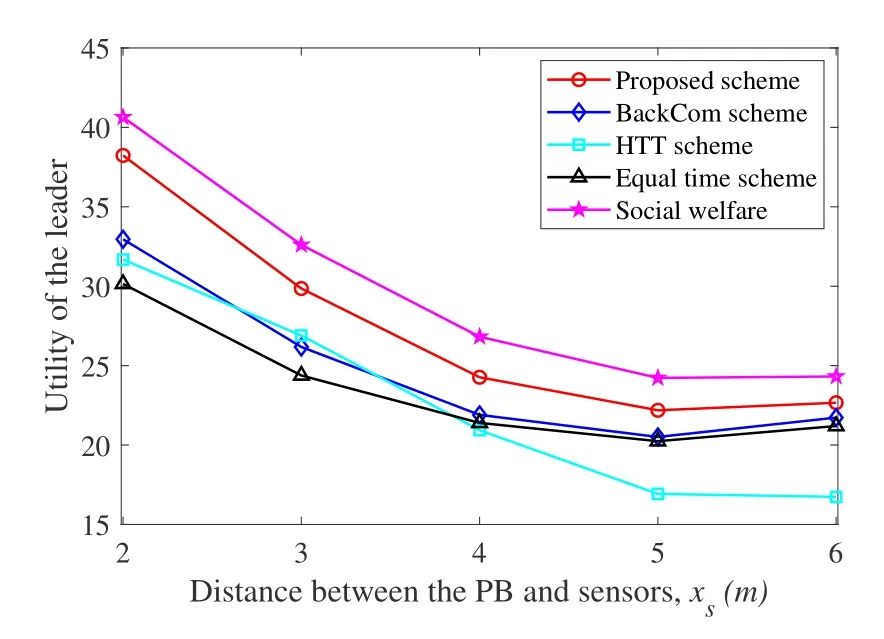
Figure 5.Utility of the leader versus xs.

In Figure 6,the impact of the distance between the PB and the AP on the utility of the leader is shown.Similar to Figure 5,the utility values of all schemes decrease when the AP is far from the PB (or sensors).It is mainly due to the fact that a longer distance between the PB and AP degrades the communication efficiency of both active information transmission and passive information backscattering.Specifically,it is observed that the gap between the proposed scheme and the HTT scheme reduces by moving the AP away from the PB.The reason is that when the AP is far from the PB,the passive backscattering efficiency is low and the active information transmission contributes more to the leader’s benefits.Furthermore,the worst performance obtained by the equal time scheme indicates that more time should be allocated to the sensors with better channel conditions.

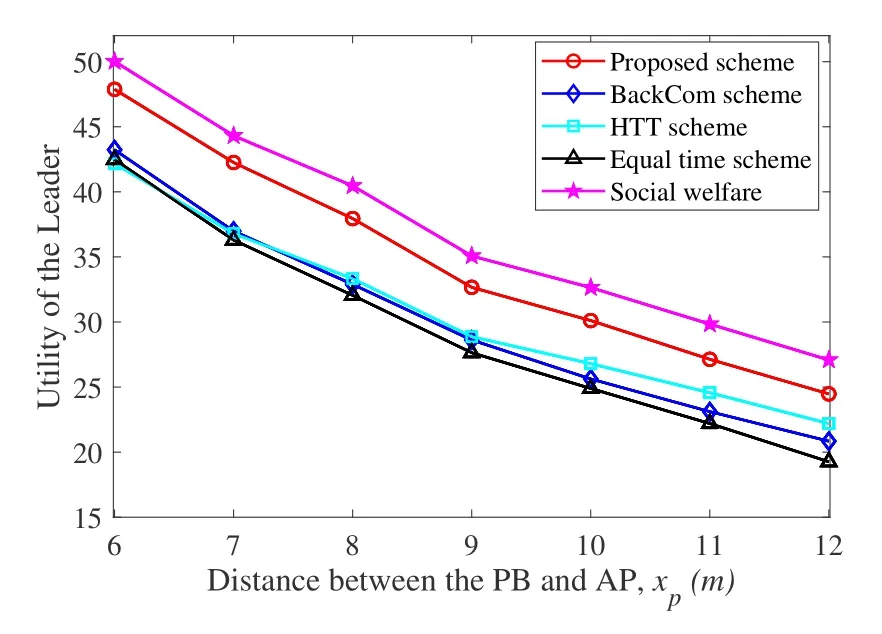
Figure 6.Utility of the leader versus xp.

In Figure 7,we study the utility variation of the follower with respect to the number of antennas at the AP.As observed in Figure 7,by deploying more antennas at the AP,the utility values of all schemes gradually improve,which is similar to the observations in Figure 4.This is due to the fact that a higher antenna gain achieved for the links from sensors to the AP enhances the total benefit (i.e.,achievable sum-rate).Thus,the leader prefers offering a higher price to buy energy from the follower.Moreover,it can be found that the utility value of the BackCom scheme is the smallest because the low communication efficiency suffered by the passive information backscattering limits the leader’s benefit.To guarantee satisfying benefits for both the leader and the follower,compared with the proposed scheme,an affordable energy price should be negotiated for the BackCom scheme,which results in a smaller utility value of the follower.

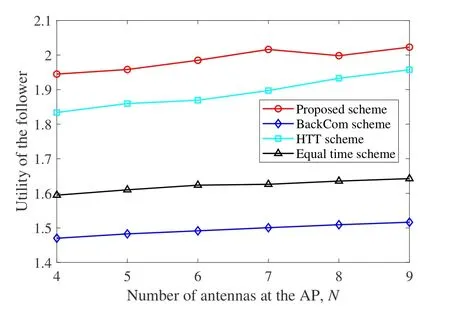
Figure 7.Utility of the follower versus N.

In Figure 8,we compare the follower’s utility obtained by all schemes versus the number of sensors.As shown in Figure 8,by deploying more sensors,the follower’s utility value of the proposed scheme increases but that of the HTT scheme reduces.It is because by deploying more sensors for the proposed scheme,the leader prefers providing a higher energy price to buy more energy to guarantee its benefit,which is a mutually beneficial and win-win result.While for the HTT scheme,as the number of sensors increases,the EH time for the HTT scheme reduces so as to allocate more time for the active information transmission,which thus regrades the follower’s utility.Again,it is found that the follower’s utility value for the BackCom scheme is smaller than that of the equal time scheme,which is consistent with the observation in Figure 7.

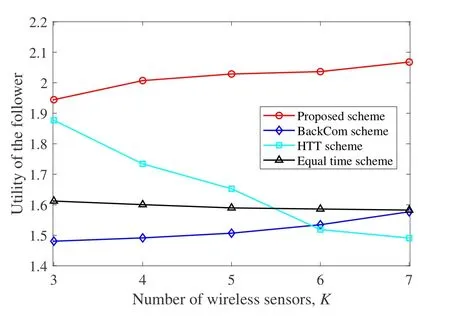
Figure 8.Utility of the leader versus K.

In the above simulations,the location of the PB is fixed.However,the PB may be mobile,e.g.,the PB is embedded in a robot [1] and an unmanned aerial vehicle(UAV)[27,28],and can move to a desired location for better performance.Against this background,we aim to optimize the location of the PB,denoted by(xp,yp),within a square with a side length of 6 m,which is illustrated in Figure 9.To achieve this goal,we consider to minimize the distance between the PB and the farthest sensor in the following problem

Figure 9.Illustration of the scenario with a mobile PB.

In Figure 10,we evaluate the effect of the PB’s location on performance enhancement.As seen from Figure 10,the optimization of the PB’s location inP6can significantly improve the utility of the leader.It is because that by optimizing the PB’s location,the distance between the PB and wireless sensors can be reduced,which thus enhances the efficiency of both WPT and passive information delivery.Similarly,the impact of the PB’s location on the system fairness is investigated in Figure 11.Specifically,the system fairness is defined as the ratio of the minimum benefit achieved by one sensor to the total benefit of all sensors,which is expressed as

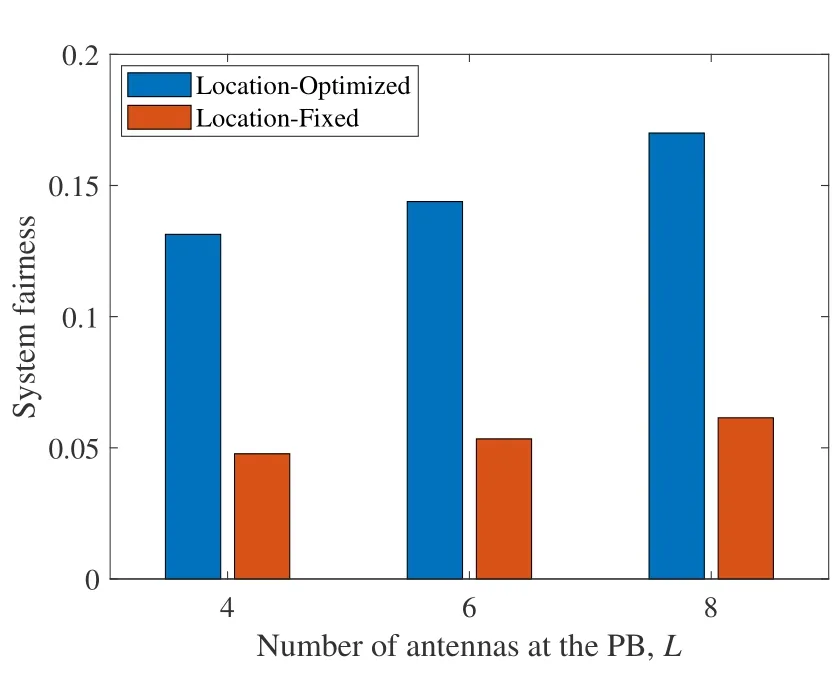
Figure 11.System fairness versus L.

whereRmin=mink{Rp,k+RA,k}.From Figure 11,we observe that by optimizing the PB’s location inP6,the minimum benefit can be improved significantly.The reason is that the location optimization guarantees that the distance between the PB and the farthest sensor is smallest,under which the farthest sensor can also have sufficient energy for passive backscattering and active transmission.

VI.CONCLUSION

In this paper,we have applied the Stackelberg game to model the energy interaction in a WPBSN,in which the PB sells energy to wireless sensors for obtaining the revenue,while wireless sensors pay for the received energy service for harvesting energy and information backscattering.We have considered the nonlinear EH model at wireless sensors to capture the realistic characteristics of the EH circuits and proposed an efficient time scheduling scheme for performance enhancement.Since the leader-level problem is non-convex,we have proposed an AO algorithm with SCA,SDR and variable substitution techniques to solve it,and proven that energy beamforming matrices obtained by applying the SDR are rank-one.Numerical results have demonstrated the superiority of the proposed scheme.It has been found that: 1) the proposed scheme can significantly improve the benefits of the leader and the follower by fully utilizing the joint passive and active information delivery;2)the resource allocation optimization has a significant impact on the system performance;and 3) the selfish maximization of the utility of service providers results in a performance loss.

In the future work,it is worth studying further performance enhancement schemes for the WPBSNs,such as reconfigure intelligent reflecting (RIS)aided scheme,massive multiple-input-multiple-output(MIMO) based scheme,rate-splitting multiple access based scheme,and so on.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China (No.61901229 and No.62071242),the Project of Jiangsu Engineering Research Center of Novel Optical Fiber Technology and Communication Network (No.SDGC2234),the Open Research Project of Jiangsu Provincial Key Laboratory of Photonic and Electronic Materials Sciences and Technology (No.NJUZDS2022-008),and the Post-Doctoral Research Supporting Program of Jiangsu Province(No.SBH20).

APPENDIX

A Proof of Proposition 1

The Lagrangian ofP3.2can be formulated as

whereµf,k,j ≥0,ξf,k,j ≥0,andΩf,k0 are the multipliers associated with the constraints C7,C10,and C11,respectively,λkis the multiplier associated with the constraintP1,k,k=Tr(hU,kP,k) derived from the objective function,andςrepresents the term unrelated withWf,k.The corresponding Karush-Kuhn-Tucker(KKT)conditions are given by

Similarly,we can also prove thatfork ∈Kare rank-one matrices.This thus completes the proof of Proposition 1.