Physical Layer Encryption of OFDM-PON Based on Quantum Noise Stream Cipher with Polar Code

Xu Yinbo,Gao Mingyi,Zhu Huaqing,Chen Bowen,Xiang Lian,Shen Gangxiang

Jiangsu Engineering Research Center of Novel Optical Fiber Technology and Communication Network,Suzhou Key Laboratory of Advanced Optical Communication Network Technology,the School of Electronic and Information Engineering,Soochow University,No.1 Shizi Street,Suzhou 215006,China

Abstract: Orthogonal frequency division multiplexing passive optical network (OFDM-PON) has superior anti-dispersion property to operate in the C-band of fiber for increased optical power budget.However,the downlink broadcast exposes the physical layer vulnerable to the threat of illegal eavesdropping.Quantum noise stream cipher (QNSC) is a classic physical layer encryption method and well compatible with the OFDM-PON.Meanwhile,it is indispensable to exploit forward error correction (FEC) to control errors in data transmission.However,when QNSC and FEC are jointly coded,the redundant information becomes heavier and thus the code rate of the transmitted signal will be largely reduced.In this work,we propose a physical layer encryption scheme based on polar-code-assisted QNSC.In order to improve the code rate and security of the transmitted signal,we exploit chaotic sequences to yield the redundant bits and utilize the redundant information of the polar code to generate the higher-order encrypted signal in the QNSC scheme with the operation of the interleaver.We experimentally demonstrate the encrypted 16/64-QAM,16/256-QAM,16/1024-QAM,16/4096-QAM QNSC signals transmitted over 30-km standard single mode fiber.For the transmitted 16/4096-QAM QNSC signal,compared with the conventional QNSC method,the proposed method increases the code rate from 0.1 to 0.32 with enhanced security.

Keywords: physical layer encryption;polar code;quantum noise stream cipher

I.INTRODUCTION

Orthogonal frequency division multiplexing passive optical network (OFDM-PON) is a promising optical access technology due to its high spectral efficiency,superior anti-dispersion property and simple equalization requirement and so on[1-5].However,the PON with the downlink broadcast is susceptible to eavesdropping and therefore the communication security is always an enduring issue.The information security at the upper layer of the optical access network is realized by the encryption algorithm and the identity authentication method in each layer of the open system interconnection reference model[6-9].Although the upper-layer security mechanism can provide security protection for the optical access network to a certain extent,the issues in the physical layer cannot be avoided.First,the encryption mechanism at the upper layer cannot protect its header and control information,and the control information of the upper layer data is easily exposed to the lower layer.Second,the physical layer may face the risk of hardware facilities being destroyed,while the upper security mechanism mainly protects binary encoded information,and cannot provide the equipment level protection required by the physical layer[10].Third,the signal transmission rate of the physical layer is high,while the upper security mechanism only protects low-speed data.Therefore,it is not sufficient to rely on the upper security mechanism to ensure the security of optical access network.The security protection of the physical layer can provide a more comprehensive security guarantee for information transmission[11-14].

Many schemes have been proposed to enhance the security of the physical layer,where the quantum noise stream cipher(QNSC)is a classic physical layer encryption method based on encryption protocol of Y-00 [15].The Y-00 protocol is well compatible with fiber optic communication facilities and the highspeed and long-distance secure transmission systems based on the QNSC have been experimentally demonstrated [15-21].To prevent the information from being cracked during transmission,the QNSC hides the plaintext information in quantum noise and amplified spontaneous emission(ASE)noise.A 70-Gb/s singlechannel 128-QAM signal was transmitted over 100 km with a net spectral efficiency of as high as 10.3 bits/s/Hz by combining the QNSC with a quantum key distribution (QKD) technique [21].If the eavesdropping is detected,the QKD will discard the key and send a new key at different times.However,the above scheme is limited to the lower QKD rate [22].Meanwhile,a two-segment silicon photonics modulator was designed for cascaded modulation to realize a 232QAM QNSC secure 320-km fiber transmission system [18].Here,the security of the system is enhanced based on the complicated hardware to increase the modulation order of signal.However,higher the modulation order is,more the required redundancy is.Meanwhile,in the QNSC system,many basis bits are required to convert a low-order signal into a highorder signal.Therefore,the long pseudo-random bit sequences (PRBS) are indispensable.Compared to the PRBS,long chaotic sequences have stronger randomness,and require less shared parameters at the transceiver.Thus,the chaotic sequences with stronger randomness were introduced to the QNSC system,which can reduce the key length for matching with the low-rate QKD transmission[20].

The forward error correction (FEC) scheme is indispensable in the PON system [6].Currently,polar code and low-density parity check code(LDPC)code are mainly FEC techniques and both are linear block codes.The polar code is based on channel polarization,and the LDPC is composed of sparse check matrix [23,24].Compared to the LDPC,the polar code has higher flexibility,which makes it more popular in the application of encryption [25].However,the improvement of transmission performance inevitably requires more redundant bits.Taking the redundant bits into account,the code rate is quite low in the conventional QNSC system when the FEC is appended.

To solve the issue of large redundancy caused by the joint encoding of QNSC and FEC,we propose a polar-code-assisted QNSC scheme.When the signal is encoded by polar code,the redundant information from the chaotic sequences is extracted.Then the data bits and the redundant bits are allocated in the high-bit positions (leftmost bits) and the low-bit positions(rightmost bits)for QNSC encoding by applying bit interleavers instead of introducing extra redundancy.The reuse of redundant information avoids additional redundant information in the QNSC encryption.During the signal transmission,the redundant information as the basis bits increases the modulation size of the encrypted signal,which makes the signal more susceptible to noise and prevents it from being eavesdropped.At the receiver,the bit allocations of the signal are restored to decrypt the data,which can be easily delivered by a secure and low-speed QKD system.We experimentally demonstrate the proposed scheme in a 12.5GBd IM/DD orthogonal frequency division multiplexing (OFDM) transmission over 30-km standard single mode fiber (SSMF) and evaluated its performance by measuring the BER curves of 16/64-quadrature amplitude modulation (QAM),16/256-QAM,16/1024-QAM,16/4096-QAM QNSC signals.Compared to the conventional QNSC method,the code rate of 16/4096-QAM QNSC signal has increased from 0.1 to 0.32 based on the proposed method.

Some schemes have also been proposed to enhance the security of the physical layer,where encryption schemes based on chaotic systems are widely used due to their high sensitivity to initial values and ergodicity [26-28].However,the chaotic system is a deterministic system and sensitive to the initial conditions.The proposed scheme combines chaotic systems with quantum noise stream,which greatly enhances the security performance of the system.Moreover,the encryption schemes in the optical domain require additional expensive optical components,which is also challenging to control the component parameters[29-31].The proposed scheme can encrypt the message with flexible algorithms in the digital domain based on the DSP at the transceiver and no more hardware is required.

The remainder of the paper is organized as follows.Section II presents the principle of the proposed polarcode-assisted quantum noise stream cipher scheme.Section III describes the experimental demonstration of the encrypted 16/64-QAM,16/256-QAM,16/1024-QAM,16/4096-QAM QNSC signals transmitted over 30-km SSMF.The performance is evaluated by measuring the BER curves and calculating the corresponding code rate.Section IV discusses the size of the key space and evaluates the security of the proposed system.Finally,Section V summarizes and concludes the paper.

The main contributions are summarized as follows:

• A polar-code-assisted scheme is proposed to improve the code rate in the QNSC system,where the polar encoding is implemented prior to the QNSC-QAM mapping,and the FEC-caused redundant bits are utilized as the basis bits for QNSC encoding.Meanwhile,the interleavers are introduced to allocate the data and redundant bits of the polar code for the QNSC encoding.Compared to the conventional QNSC scheme,the extra redundancy of FEC is eliminated in the proposed scheme and the code rate of 16/4096-QAM QNSC signal is experimentally improved from 0.1 to 0.32 and the BER performance is improved by 0.5 dB.

• Meanwhile,a chaotic system is introduced to generate basis states.Here,three parameters are needed to yield chaotic sequences with infinite length,which greatly reduces the requirement for the transmission rate of the QKD system and improves the security of the system.

• The security of the system is evaluated based on the key space and the probability of successful detection to the QNSC signal at the illegal end.

II.PRINCIPLE OF THE PROPOSED POLAR CODE-ASSISTED QNSC SCHEME

In this section,the basic principles of quantum noise stream cipher,chaotic sequence and systematic polar code are first introduced,which underlies the analysis and design of the proposed polar code-assisted QNSC scheme.

2.1 Quantum Noise Stream Cipher

QNSC is a physical layer encryption technique with high security in optical fiber communication,where ASE noise from transmission links with erbium-doped fiber amplifiers (EDFAs) overwhelms quantum noise of transceiver [15-21].QNSC relies on the characteristic of higher-order modulation signals susceptible to noise.Hence,a lower-order QAM signal(plaintext)with spare constellation distribution is converted into a higher-order QAM signal(ciphertext)with dense constellation distribution.Without the key,it is challenging to recover the plaintext.

In order to generate the encrypted higher-order QAM signal,amounts of redundant bits are required as the base to scramble the lower-order signal with the plaintext information.The addition of redundant basis bits converts the lower-order QAM signal to higherorder QAM signal.Meanwhile,with the increase of modulation order,the minimum Euclidean distance of constellation points in the constellation diagram decreases,and thus the constellation points are more likely to be overlapped during transmission.For the illegitimate receiver,it is challenging to restore the original transmitted information from the blurred constellation diagrams.Contrarily,for the legitimate receiver,the plaintext information hidden in the noise can be extracted with the keys even if the signal has been drowned in noise.

Figure 1 illustrated the architecture of a conventional QNSC system.First,a PRBS is introduced to provide redundant key bits (denoted as BasisB),shared between the transmitter and the receiver.Generally,a linear feedback shift register with seed keys can be utilized to generate the PRBS.BasisBis denoted as basic states,which is used for data scrambling.If the transmitter with the plaintext dataX=(XI,XQ) is directly modulated into a lower-order QAM signal,it will be exposed to eavesdroppers.

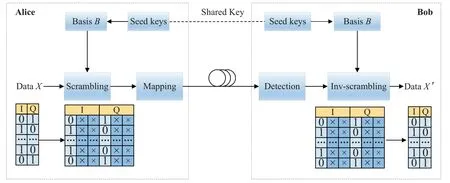
Figure 1.The architecture of a conventional QNSC system.

Therefore,the plaintext dataXand the basisBare jointly coded to obtain the scrambled higher-order QAM signal with the ciphertext dataS=(SI,SQ)=(XIBI,XQBQ).Here,the redundant key bitsBare appended to the plaintext bitsX.Assuming that the dataXand basisBconsist ofmandnI/Q bits per symbol,respectively,then the generated encrypted dataSwill have (m+n) I/Q bits.After then,the ciphertext is mapped into a higher-order QAM signal for transmission.Finally,the signal is detected and decoded with the basisBof the shared key to yield the original plaintext information.

Figure 2 shows the constellation diagram of a 16/64-QAM QNSC signal,where the 16-QAM signal carries the plaintext data and is encrypted into the 64-QAM signal.For the encrypted 64-QAM signals,each symbol consists of 3 I/Q bits respectively.The first two bits of I/Q bits are used for the 16-QAM signal of the plaintext data and the remained 1 bit from the basis state is used for scrambling the message.For example,the constellation point A=(I,Q)=(101,010) carries the actual plaintext information(10,01).Compared to the 16-QAM signal,the encrypted 64-QAM signal requires higher optical signal to noise ratio(OSNR)for desired BER performance.The eavesdroppers always need to capture the encrypted 64-QAM signal with higher OSNR for further decryption,which becomes more challenging for higher-order QAM signals,such as 1024-QAM and 4096-QAM signals.

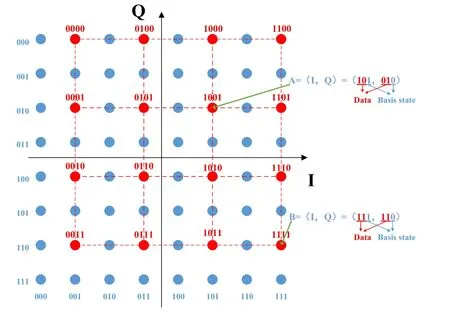
Figure 2.The constellation diagram of the 16/64-QAM QNSC signal.

The decoding of QNSC signals only requires the correct bits,i.e.,leftmost bits of I/Q bits.In our previous work,an improved decoding method based on the priori basis states was used to improve system performance [20].According to the basis states shared between the transmitter and the receiver,the encrypted 64-QAM signal is composed of various 16-QAM constellation points.For example,the basis state of (1,0) determine the 16-QAM constellation points,shown by red dots in Figure 2.By calculating the Euclidean distance from the received symbol to the various 16-QAM constellation points determined by the basis states,we can yield the minimum Euclidean distance as the correct position of the symbol and decode it.For example,if a symbol has a minimum Euclidean distance to the point B=(111,110) with the basis states (1,0),it will be decoded as (11,11).The above method can improve the accuracy of the decoding of the QNSC signal.

2.2 Chaotic Sequence

In the conventional QNSC system,the basis states used to scramble the plaintext information is randomly generated and it is very challenging for key distribution systems to transmit amounts of keys,such as QKD with low transmission speed [22].In order to reduce the key length for transmission and add the decoding barriers of polar code for eavesdroppers,a chaotic sequence is applied as BasisBin this work.Chaotic sequences are random and more sensitive to initial values,where only three parameters are required to be shared between the transmitter(Alice)and the legitimate receiver (Bob) in Figure 1.For the issue to generate and transmit amounts of shared basis bits in the QNSC system with the encrypted higherorder QAM signals,the discrete chaotic system will be a good solution.In order to reduce the complexity of the key,an optimized logistic mapping model is applied[32],

wherendenotes the number of iterations,{xn,n=1,2,...,N}is theN-iteration result of the initial valuex0,which ranges between-1 and 1,andµis the bifurcation parameter.

Figure 3 illustrates the variation of chaotic sequence versus the bifurcation parameterµ.For 0＜µ ≤0.8,there is a fixed output for eachµ.With the increase ofµvalue to 0.8＜µ＜1.4,the logistic map exhibits the phenomenon of periodic doubling.It can be clearly seen that the system enters the chaotic state completely with 1.4≤µ ≤2.The important feature of chaotic sequences is their extremely sensitivity to parameters.In order to demonstrate the high sensitivity of chaotic sequences to parameters,the parameters are set asn=1000,µ=1.9125,x0=0.61854654500112.For comparison,we slightly change the initial value tox,0=0.61854654500113,which has a subtle variation and the other parameters remain unchanged.

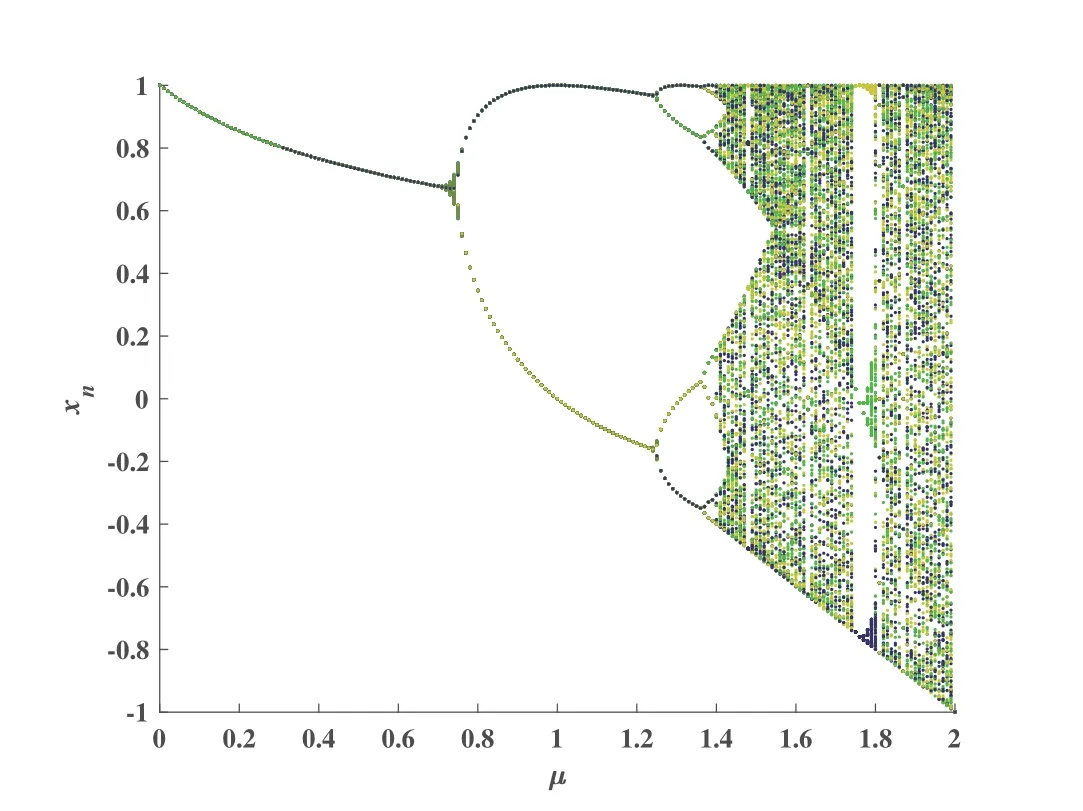
Figure 3.Chaotic sequence vs. the bifurcation parameter.

Figure 4a and 4b show the auto-correlation function forx0,and the cross-correlation function ofx0andx,0.The auto-correlation function defines the similar-ity of the signal between a given time and a lagged time by comparing the value at the timetto that at a successive timet+τ.Here,τis a time interval.A rapidly fluctuating signal has an autocorrelation function that decays quickly with respect toτ,as shown in Figure 4a.The cross-correlation function measures the similarity between a signal and the lagged copy of another signal with the time lagτ.If the crosscorrelation coefficient is close to zero,these signals are entirely different,as shown in Figure 4b.As shown in Figure 4a and 4b,whenτ0,the autocorrelation coefficient approaches zero,while the cross-correlation coefficient of two chaotic sequences with different initial values are close to zero,regardless of the value ofτ,which verifies that the generated chaotic sequence is highly random.

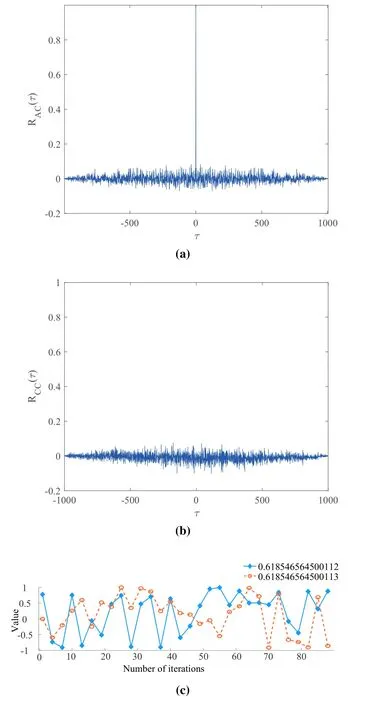
Figure 4.(a) Auto-correlation of x0 (b) cross-correlation of x0 and x,0 (c)values of chaotic sequences with different initial values.

Figure 4c shows the generated chaotic sequences with the above two initial values,where the iterations of the chaotic sequence have two completely different tracks.Thus,no one has access to the plaintext information except the legitimate recipient.Even if the information is intercepted by eavesdroppers without correct keys,the cracked message will be completely wrong.Therefore,the transmitter can generate a set of infinitely long chaotic sequences to encrypt plaintext messages by three parameters,n,µ,andx0.The application of chaotic sequences simplifies the key structure,and effectively resists selective plaintext attacks,making encrypted information more reliable.

Finally,the generated chaotic sequences are processed by a trimmer in Eq.(2)with a suitable threshold.Generally,the threshold is set to zero.After the trimmer,the chaotic sequence is transformed to a binary sequence,which is used for redundant key bits in this work.

2.3 Systematic Polar Code

In the conventional QNSC system,many reductant basis bits are introduced to convert the lower-order QAM signal to the higher-order QAM signal by appending the basis bits to the plaintext information bits.Meanwhile,the FEC is required for a communication system to improve the transmission performance by sending redundant error correction code.It may be feasible to share these reductant bits between the QNSC and the FEC.

Meanwhile,polar code as a popular FEC code can asymptotically achieve Shannon’s limit and have the characteristics of low complexity and error-floor free.The systematic polar code(SPC)is an improvement of the general polar code and has enhanced error correction performance[33].The complexity and flexibility of SPC are more suitable for improving the security of encrypted communication system and increasing the difficulty of decoding for eavesdroppers.

First,the concept of channel polarization is introduced [34].If the binary symmetric channel is combined and split in a specific way,the split bit channel will be polarized.The channel capacity of a part of the bit channel will converge to 1.On the contrary,the channel capacity of another part of the bit channel will become small and converge to 0.The former is called as ‘good channel’,and the latter as ‘bad channel’.When the number of channels is increased to an infinity,the above channel polarization is more obvious.

The polar code is based on channel polarization.Assuming thatWis a symmetric binary-input discrete memoryless channel andW:U →Ywill be calculated.W(y|u)represents transition probability.

Figure 5a illustrates that two symbols are sent in a symmetric memoryless channel and the transition probability is written as.

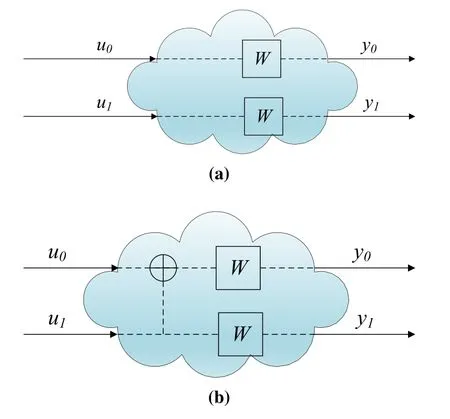
Figure 5.Two symbols transmission in (a) a symmetric memoryless channel(b)a combined channel.

Figure 5b illustrates that two symbols are sent in a combine channel,where⊕denotes the XOR operation.When two channels are combined,the transition probability is written as[35].

This is the basic unit of channel combination.In the recombined channelW2,the transmitted information{u0,u1}is defined asand similarly,the information with channel encodingcan be obtained.

TheG2is the generation matrix.Similarly,W4can be obtained fromW2.Recursively,WNcan be formed by the combination of twoWN/2withNchannels.

The arbitrary generation matrixGNcan be written as,

whereF=G2=[1 0;1 1],BNis a bit-reversal permutation matrix.The symbol⊕is the Kronecker inner product.

Meanwhile,the Bhattacharyya parameter is used to evaluate the quality of the information channel,defined as an integral function,

whereσ2is the variance of the additive Gaussian white noise channel.W(y|0) andW(y|1) are the channel transition probability.The channel with largeZ(W)is used to load frozen bits.

The systematic polar code is cascaded by two general polar codes and the encoding process consists of two parts.Figure 6 is the schematic diagram of the SPC encoding with the code lengthNof 8.Here,the frozen bits are marked in blue and the information bits are marked in black.Usually,all frozen bits are set to zero.In this work,in order to enhance the security,a part of generated chaotic sequence is used as the frozen bits.The transmitter and the receiver share the parameters of the chaotic sequence as the keys to determine values of frozen bits for decoding.

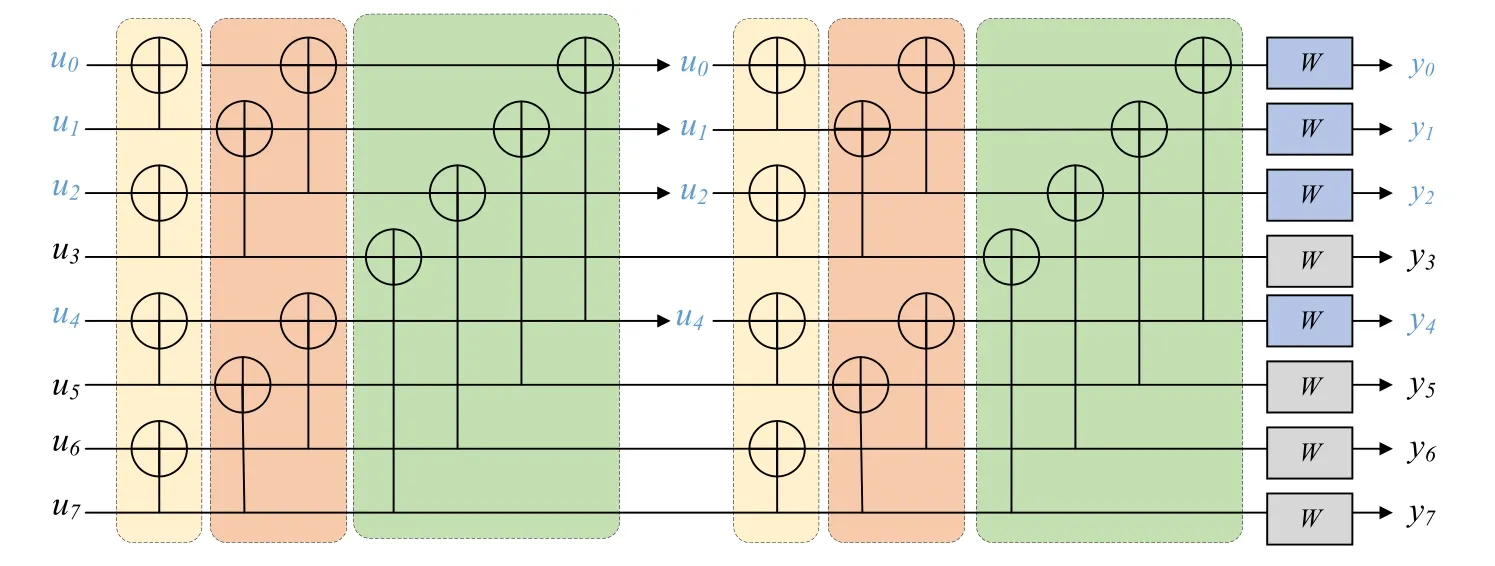
Figure 6.Block diagram of SPC encoding with code length N of 8.

For the decoding,the successive cancellation (SC)decoder is utilized [35].Fori ∈{1,2,...,N},the value of thei-th code is calculated according to the current received code and the priori-1 codes.If thei-th channel is assigned for frozen bits,the original frozen bits can be loaded directly.The decoding information at the receiver is denotes as,

where{ui,i ∈AC}stands for frozen bits,which is shared between the transmitter and the receiver.On the other hand,{ui,i ∈A}stands for information bits,decoding based on the decision function.

The log-likelihood ratio(LLR)ofis calculated to decode information.

2.4 The QNSC with Polar Code

In the conventional QNSC scheme,amounts of reductant basis bits are required.Meanwhile,the security of the QNSC system is enhanced by increasing the modulation order,which brings a higher redundancy.In order to efficiently reuse these reductant bits and increase the code rate,we will share the reductant bits between the QNSC and the FEC.Figure 7 shows the block diagram of the proposed QNSC with polar code.First,a chaotic sequence is generated.Second,a XOR operation is implemented between the plaintext information and the chaotic sequence.Then,the information of the above preliminary encryption is encoded by the systematic polar code.The encoded information is divided into the information bits and the redundant frozen bits.If the encoded signal is directly launched into the fiber,it is exposed for an eavesdropper to decipher the plaintext information.Thus,the QNSC technique is applied to enhance the security of the system.The QNSC requires the basis bits to scramble plaintext information.If the redundant bits generated in polar code are reused as the basis bits of the QNSC,it is not necessary to introduce new redundant bits.Hence,we use the interleaver to reshape the information and frozen bits by allocating the information bits at the leftmost bits of the QAM signals and the frozen bits at the rightmost bits of the QAM signal.As shown in Figure 7,after the SPC encoding with code length N,the bit allocation is implemented as required by the QNSC with the operation of the interleaver,where the orange indicates the information bits and the blue denotes the frozen bits.Finally,the bits are mapped into the QAM symbols and then the generated QAM signal is modulated into the optical signal and launched into the fiber.At the receiver,the reverse process of encryption is implemented to achieve the plaintext message.First,the received encrypted QNSC signal is demodulated to obtain the binary data information according to the basis states generated by the shared key.Then,the inverse interleaver is exploited to recover the position of the information bits and frozen bits of the QNSC signals composed of the obtained data information and basis states again and the polar code is decoded based on the known frozen bits.Finally,the XOR operation is implemented between the decoded ciphertext and the chaotic sequence,and then the plaintext information is obtained.By the joint coding of the polar code and the QNSC with the shared reductant bits,the code rate will be increased with the improved transmission performance.

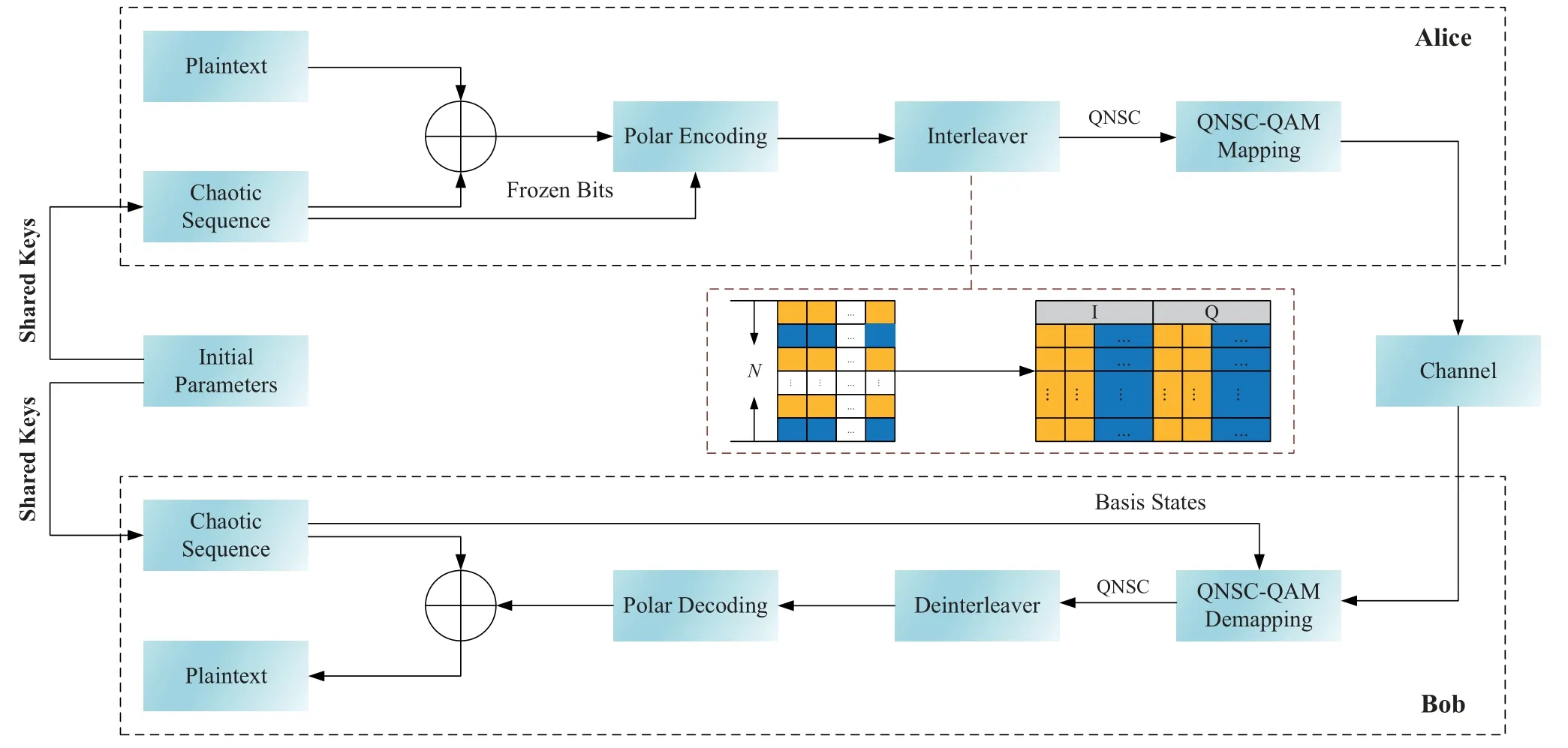
Figure 7.Block diagram of the proposed polar-code-assisted QNSC encryption scheme.

III.EXPERIMENTS AND RESULTS

The proposed polar-code-assisted QNSC scheme is demonstrated in a 30-km OFDM-PON transmission system and the experimental setup is shown in Figure 8.The signal is generated at the transmitter side by the offline digital signal processing (DSP).The generated signal is sent to an arbitrary waveform generator (AWG) with a sampling rate of 50 GSa/s for digital-to-analog(DA)conversion.Hermitian symmetry is applied to generate the real-valued time-domain OFDM signals.The electrical signal from the AWG is modulated by a Mach-Zehnder modulator(MZM)and a continuous wave (CW) laser at 1550.116 nm into an optical signal,which is transmitted over a 30-km SSMF.Before the signal enters the receiver,we use a variable optical attenuator (VOA) and an erbiumdoped fiber amplifier (EDFA) for noise-loading and the following VOA is used to adjust the signal power to ensure the linear response of the 10 GHz photodetector (PD).The optical signal is converted into an electrical signal by the PD.Finally,a real-time oscilloscope with a sampling rate of 50 GSa/s acquires the data for the processing of the offline DSP.Moreover,in the OFDM experiment,the number of total carriers is 512 and the number of data carriers is 128,located from the 129th to the 256th subcarriers.To reduce the effect of beat-frequency interference,the first 128 subcarriers are set as null carriers.On the other hand,the chaotic sequence is mainly generated by three main parametersn,µ,x0,with the values of 1200,1.9125,0.61854654500112.

Figure 8.Experimental setup of the proposed polar-code-assisted QNSC scheme in a 30-km OFDM-PON transmission system.

Figure 9 shows the constellation diagram of 16/256-QAM QNSC signal without and with decryption when the received optical power is-19 dBm.The 16-QAM signal is hidden in the constellation diagram of 256-QAM signals.For the noise-distorted signal,it is challenging for eavesdroppers to decipher plaintext messages,as shown in Figure 9a.

Figure 9.Constellation diagram of 16/256-QAM QNSC signal(a)without decryption and(b)with decryption.

The code rate can be obtained by,

whereflooris the round down function,Nis the length of each group of polar codes,Kis the length of the plaintext information in each group of polar codes,nis the length of basis states for I or Q andmis the length of the data bits for I or Q.In the experiments,Nis set to 256.Here,the signals of various modulation format have different code rates.For example,for the 16/256-QAM QNSC signal,the transmitted 256-QAM signal has 4 I/Q bits respectively,and the plaintext message is loaded into the 16-QAM signal with 2 I/Q bits.A group of polar code can be divided into exactly 32 16/256-QAM symbols.Therefore,the plaintext information in each group of polar codes has 128 bits.Obviously,both plaintext and redundant information possess half of the bits,and the code rate is 50%.Similarly,for the 16/64-QAM signal,the code rate is about 66.6%.Different from the 16/256-QAM signal,4 bits of polar code are discarded to obtain 42 16/64-QAM symbols.Thus,η=66.6% can be obtained.Here,the redundant information generated in the polar code is used for QNSC scrambling and the length of the plaintext message is set to approximate 32,000 bits.

Figure 10 illustrates the code rates of different QNSC signals in the QNSC system combined with traditional LDPC or polar code and the proposed polarcode-assisted QNSC scheme.The code rates of 16/64-QAM,16/256-QAM,16/1024-QAM and 16/4096-QAM in the traditional LDPC or polar code system are 0.44,0.25,0.15 and 0.1 because of the accumulated redundancy from the QNSC and the FEC.In comparison,in the proposed polar-code-assisted QNSC system,the code rates of 16/64-QAM,16/256-QAM,16/1024-QAM and 16/4096-QAM are respectively increased to 0.67,0.5,0.39 and 0.328.It is obvious that the code rates decrease more with the increase of the modulation order.Moreover,the security of QNSC scheme highly depends on the modulation order of encrypted signal,and thus large redundancy is induced,where the proposed scheme will be a good solution to the issue of large redundancy[16,18,19].

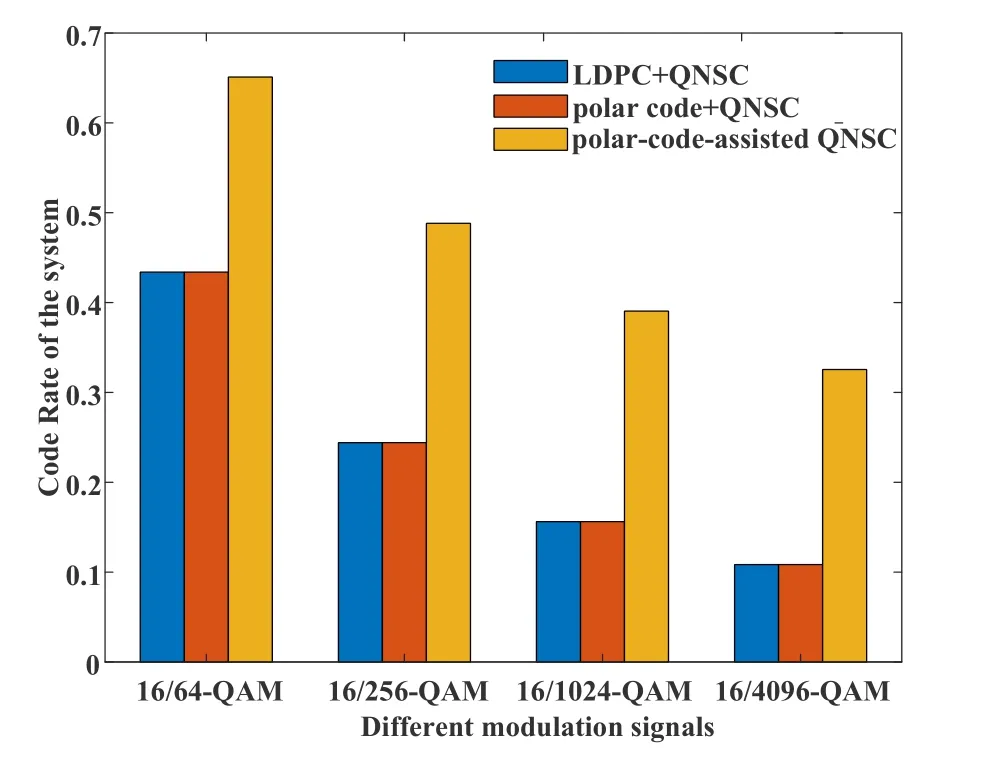
Figure 10.Code rate of different signals with various encryption schemes.

We experimentally measured the BER curves of 16/64-QAM,16/256-QAM,16/1024-QAM,16/4096-QAM QNSC signals at 12.5GBd for back-to-back(BTB)and 30-km SSMF transmission.The measured BERs in the cases of the BTB and the 30-km SSMF transmission are shown by solid and dashed curves in Figure 11,respectively.The penalties caused by the 30-km SSMF transmission is negligible because of the superior anti-dispersion property of 12.5GBd OFDM signal.In the conventional QNSC encryption scheme,the polar code has contributed slight improvement in the BER performance,as shown by pentagonand triangle-marked curves in Figure 11.Compared to the conventional QNSC scheme,the proposed method can achieve approximately 0.5-dB improvement in the error-free case,as shown by circle-marked curves in Figure 11.In the proposed scheme,all information bits are allocated in the leftmost by the interleaver and these information bits are modulated into lower-order QAM signal with the enhanced tolerance to the noise,which contributes to the improvement of BER performance.Therefore,the proposed scheme not only increases the code rate but also improves the BER performance.

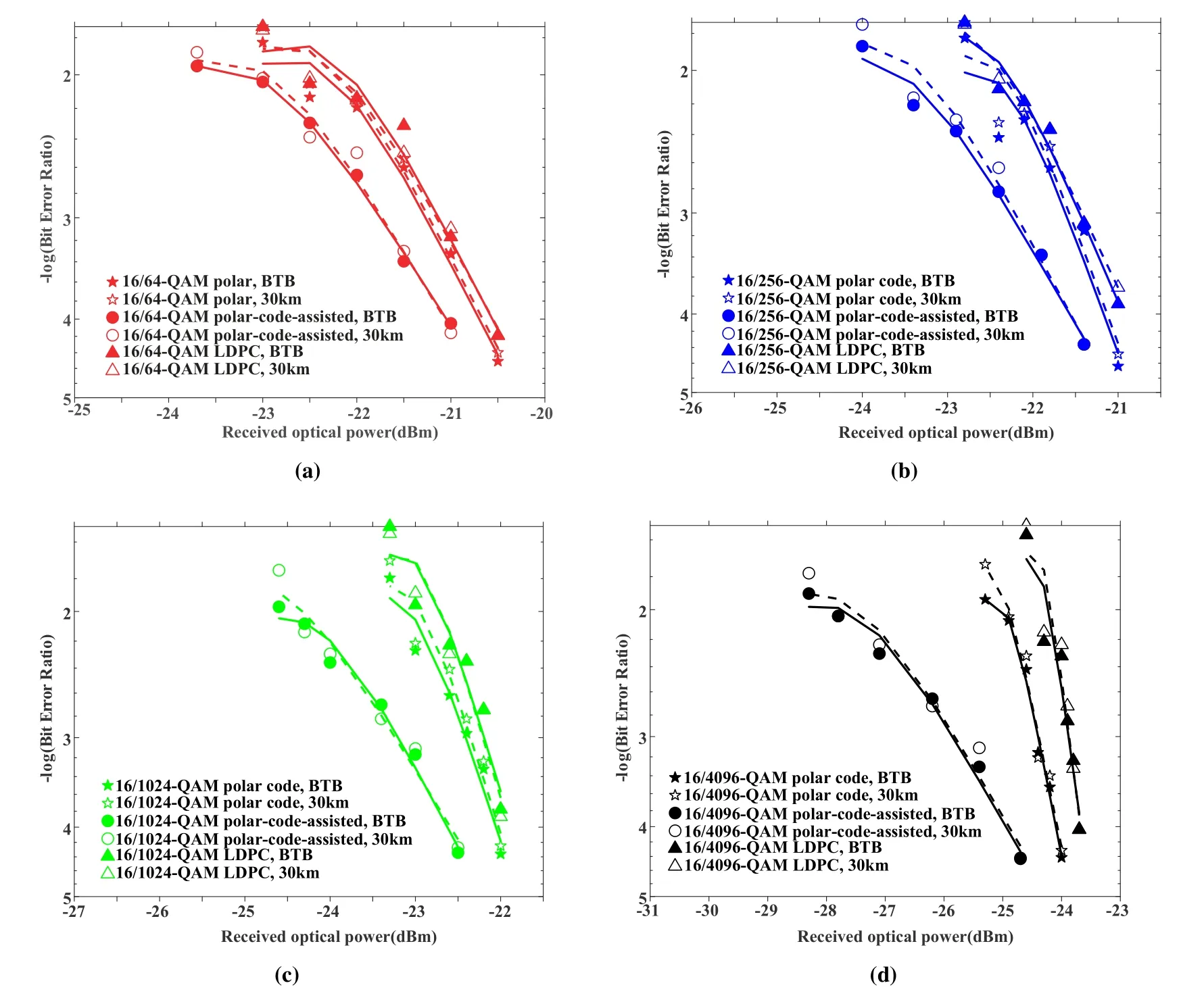
Figure 11.Measured post-BER curves of (a) 16/64-QAM, (b) 16/256-QAM, (c) 16/1024-QAM, (d) 16/4096-QAM QNSC signals vs. received optical power(dBm).

IV.SECURITY ANALYSIS

Generally,the exhaustive search attack is the most common attack method.Here,the eavesdroppers usually explore all possible keys in the key space until the correct key is found.Compared to the conventional QNSC encryption,the proposed encryption algorithm has an enhanced security due to the increased complexity of chaotic sequences and interleavers.

The complexity of the chaotic sequence,mainly depends on the three initial valuesµ,n,x0.The precision of the key{µ,x0},{µ+Δµ,x0+Δx0}is used to quantify the security enhancement.As the discussion in the section 2.2,µandxdetermine the degree of chaos and the varying track of chaotic sequences,which has a significant influence on the BER performance,as shown by triangle-and circle-marked curves in Figure 12.As shown in Figure 12,a trivial variation of initial valuesµandxwith an order of magnitude deviation (10-16～ 10-15),leads to the decoding errors.Therefore,a large key space ofs1=1016×1015=1031can be achieved.On the other hand,the interleavers are involved in the proposed scheme.If the illegitimate receiver has no any information of correct interleaving order,it will be impossible to crack the ciphertext.Thus,the complexity of the interleaver also can enhance the security,which is related to the number of information bitsK.The interleaver mainly is exploited to rearrange the information bits and the key space is obtained bys2=2K.Here,s=s1s2represents the size of the key space for exhaustive computation.

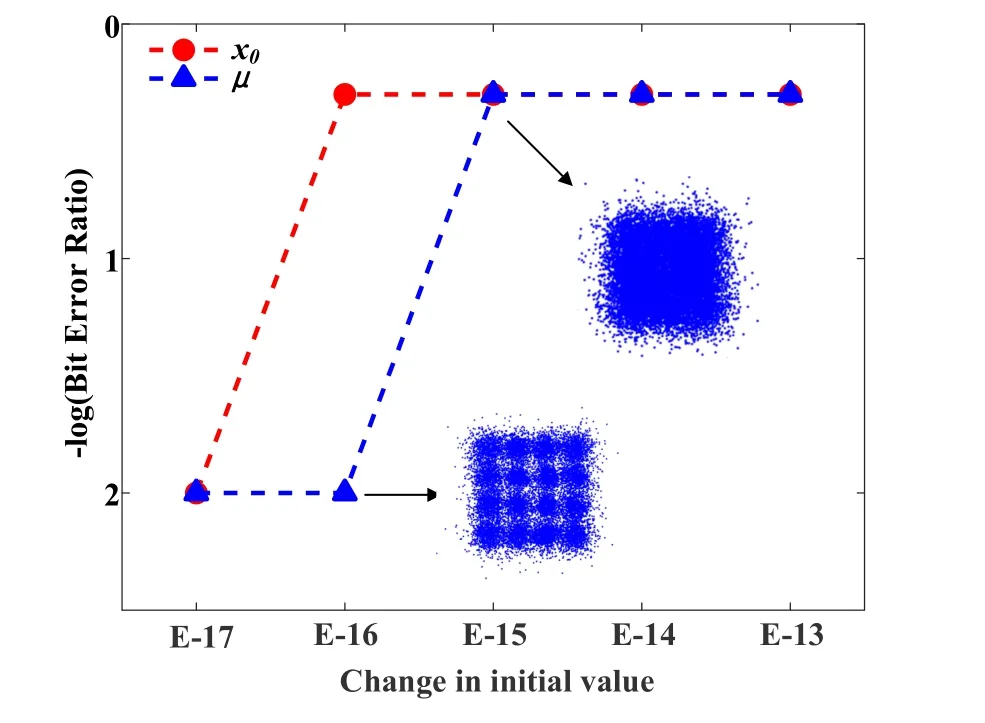
Figure 12.BER versus initial value error of chaotic sequence.

Since the QNSC signal is transmitted in the classical channel,the noise distribution of the eavesdropper is consistent with that of Bob.Thus,we can estimate the demodulation performance of the eavesdropper by calculating the noise distribution of Bob [21].Figure 13 illustrates the noise distribution of the recovered 16/4096-QAM signal in the case of BTB when the received optical power is-24 dBm,i.e.,the lowest receiver power to guarantee the error-free condition.In order to ensure that the SNR of the eavesdropper is as large as possible,we choose the noise distribution in the case of BTB.First,the constellation amplitude is normalized with±1.Then,the noise variances of the 16/4096-QAM signal are calculated as follows,

Figure 13.Noise distribution of recovered 16/4096-QAM signals with the received optical power of-24 dBm in the case of BTB.

The normalized minimum separation between symbols and the number of masked signals of 16/4096-QAM can be expressed as[16,19],

whereMis the I/Q modulation order of the encrypted 16/4096-QAM signal.Only one of the Γ symbols is correct,hence 1/Γ denotes the probability that the encrypted constellation point is kept at the original location,i.e.,‘success’ probability.When the received power is -24 dBm,the values of Γ are 1.4,6.3,27.1 and 111.6 for 16/64-QAM,16/256-QAM,16/1024-QAM and 16/4096-QAM respectively.Thus,it is straightforward to enhance the security of the system by increasing the modulation order.The security levelQcan evaluate the ability to resist brute force attacks[16,21],

whereβ=κ/2n,κis the length of basis state sequence andnis the length of the I/Q basis state of each QAM symbol.In this work,the basis state sequence intercepted from the chaotic system is used to encrypt exactly all the plaintext information.The length of plaintext message is 32,000 bits andβis 8000.When the plaintext information is encrypted into 16/4096QAM symbols,Qis 111.68000.Therefore,the scheme is extremely robust against brute force attacks.

V.CONCLUSION

In general,FEC is indispensable in optical communication systems to improve the BER performance.However,when FEC is appended to the QNSC systems,large redundancy is induced.In this work,we propose a polar-code-assisted QNSC scheme,where information bits and the redundancy of polar code are distributed in high and low bits of the QNSC signals respectively by interleavers to reuse polar code redundancy instead of introducing extra redundancy.Compared to the conventional QNSC system with the FEC,the code rate of the proposed scheme is improved from 0.1 to 0.32 for 16/4096-QAM QNSC signals,and the scheme simultaneously yields a BER improvement of about 0.5-dB.Moreover,a chaotic system is introduced to generate basis states of QNSC signals,which not only reduces the requirement of QKD system rate,but also enhances the security of the system.

ACKNOWLEDGEMENT

This work was supported in part by the National Natural Science Foundation of China Project under Grant 62075147 and the Suzhou Industry Technological Innovation Projects under Grant SYG202348.