Power Allocation for SE Maximization in Uplink Massive MIMO System Under Minimum Rate Constraint

Wang Hui ,Yu Xiangbin,2,* ,Liu Fuyuan ,Bai Jiawei

1 College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China

2 Key Laboratory of Wireless Sensor Network and Communication,Shanghai Institute of Microsystem and Information Technology,Chinese Academy of Sciences,Shanghai 200050,China

Abstract: In this paper,we optimize the spectrum efficiency(SE)of uplink massive multiple-input multiple-output(MIMO)system with imperfect channel state information(CSI)over Rayleigh fading channel.The SE optimization problem is formulated under the constraints of maximum power and minimum rate of each user.Then,we develop a near-optimal power allocation(PA)scheme by using the successive convex approximation(SCA)method,Lagrange multiplier method,and block coordinate descent (BCD)method,and it can obtain almost the same SE as the benchmark scheme with lower complexity.Since this scheme needs three-layer iteration,a suboptimal PA scheme is developed to further reduce the complexity,where the characteristic of massive MIMO (i.e.,numerous receive antennas) is utilized for convex reformulation,and the rate constraint is converted to linear constraints.This suboptimal scheme only needs single-layer iteration,thus has lower complexity than the near-optimal scheme.Finally,we joint design the pilot power and data power to further improve the performance,and propose an two-stage algorithm to obtain joint PA.Simulation results verify the effectiveness of the proposed schemes,and superior SE performance is achieved.

Keywords: imperfect CSI;massive MIMO;minimum rate constraint;power allocation;spectral efficiency

I.INTRODUCTION

As one of the key technologies in the fifth generation (5G) wireless communication systems,massive multiple-input multiple-output(MIMO)systems have been investigated extensively in wireless communication systems for their economic components,security and huge enhancement in spectrum efficiency (SE)[1,2].Effective power allocation (PA) among users can significantly improve SE performance of massive MIMO systems,which has attracted a great deal of attention[3,4].

The effect of PA is decided by the quality of channel state information (CSI) at the receiver and the transmitter,which is helpful in removing the multi-user interference in massive MIMO systems.Nonetheless,the receiver is unable to obtain perfect CSI in practical wireless systems because of feedback delay,estimation error and so on[5].

Meanwhile,the quality of service (QoS) requirements need to be met in order to ensure the user experience[6,7].

Massive MIMO systems have received considerable attention in both academic and industry domain.Authors of [8] developed a two-stage precoder using the signal-to-leakage-plus-noise ratio metric for frequency-division duplexing (FDD) massive MIMO systems.In [9],the channel estimation and hybrid combining problems in wideband Terahertz massive MIMO with uniform planar arrays was addressed.Authors of[10]gave the SE analysis of the zero-forcing(ZF)detector in cell-free massive MIMO systems with perfect CSI and imperfect CSI,respectively.

SE performance of massive MIMO systems and its optimization with respect to PA have attracted lots of interests [11-13].Reference [14] obtained expressions of the achievable uplink SE in massive MIMO systems with perfect and imperfect CSI,respectively,where equal PA is assumed,and the linear receivers considered included ZF,maximum-ratio combining(MRC)and minimum mean-square error(MMSE)receivers.Authors of[15]derived the lower bound of SE performance in a uplink massive MIMO system with Jensen’s inequality,and optimized the PA under maximum power constraint.The authors of[16]jointly optimized pilot and payload power to maximize the sum SE and the minimum SE among users,respectively.The sum SE optimization problem,where the number of active users is varying,was analyzed in multi-cell massive MIMO systems in[17].In[4],the optimizations of uplink SE and energy efficiency (EE)performances under massive MIMO systems with target bit error rate and imperfect CSI are investigated.

Meanwhile,the guarantee of QoS requirements,e.g.,rate requirements,is also one main objective of wireless communication system.In [18],the authors jointly selected the fronthaul links and optimized the transmit precoding matrices to maximize the EE of a multiuser MIMO aided distributed antenna system,considering the rate requirements and the power constraints of the remote access units.In [19],the EE is optimized through PA under QoS constraints,based on mathematical equivalence and dual composition.

The authors of [20] proposed a PA algorithm for maximizing the defined effective capacity (EC) and effective-EE over MIMO broadcast channels under individual QoS constraints.In [21],the authors minimized the total downlink power consumption at the APs,considering both the maximum downlink power of each AP and the SE requirement of each user.

Furthermore,PA solutions for a multiple user-type massive MIMO system are proposed in [22],which guarantee QoS for part of the users and maximize the sum-rate of the other users at the same time.

The authors of [23] solved the data rate maximization problems by jointly optimizing the pilot and payload transmission power for both MRC and ZF,considering the energy constraint and the minimum data rate requirement for each device.

Unfortunately,the above works do not consider SE maximization of uplink massive MIMO systems with minimum rate constraint of each user.In addition,most works on QoS requirements are based on dual decomposition,which needs multi-layer iteration,leading to high complexity.Therefore,it is necessary to optimize power allocation to maximize SE under imperfect CSI over Rayleigh fading channels,considering minimum rate constraints,and propose a low complexity method.The main contributions of the paper are summarized as follows:

1) The closed-form uplink SE expression of massive MIMO system over the Rayleigh fading channel is obtained according to [14],where MMSE estimation is adopted.Then we formulate the optimization problem to maximize the SE under the minimum rate constraint and maximum power constraint.Successive convex approximation(SCA)is applied to transform the non-convex optimization problem to a convex one,whose parameters can be solved iteratively.Then the Lagrangian is deduced based on the objective function and the constraints.Finally,the block coordinate descent(BCD)method is used to obtain the PA,and the Lagrange multipliers can be solved iteratively with sub-gradient algorithm.

2) Considering that the above algorithm needs treelayer iteration,we propose a suboptimal scheme,which utilizes the feature of massive MIMO,i.e.,numerous antennas,to convert the objective function to a concave function,and transforms constraints to upper bound and lower bound of powers.The suboptimal scheme only needs singlelayer iteration,leading to smaller number of iterations.However,its SE performance is similar to that of the near-optimal scheme in 1),especially when there are numerous receive antennas.In conclusion,it is effective and reliable in massive MIMO systems.

3) To further improve the SE,we give the joint PA design of pilot and data.Correspondingly,the joint optimization problem is formulated to maximize the sum SE,and an effective iterative algorithm based on the BCD method is presented to find the solution,where closed-form data power is deduced given the pilot power,and closedform pilot power is also attained give the data power.Simulation results show that the joint design scheme of pilot power and data power can obtain higher SE than the near-optimal and suboptimal schemes with optimizing the data power only.This is because the pilot power is optimized for the former,while for the latter two,the pilot power is fixed.

The other sections are organized as follows.In Section II,we model the uplink massive MIMO system,estimate the channel with MMSE estimator,and obtain the closed-form SE and its asymptotic expression.In Section III,a near-optimal PA algorithm is proposed by the SCA,sub-gradient and BCD methods.We propose a suboptimal PA scheme by using the asymptotic SE expression and converting the rate constraint to upper bound and lower bound of powers in Section IV.In Section V,joint optimization of pilot and data powers is solved.Simulation results is provided in Section VI,and Section VII summarizes this paper.

Notations: Throughout this paper,(·)Hdenotes the conjugate transpose,(·)-1denotes the inverse operators.Cm×nstands for am×ncomplex matrix.Inis an-th order identity square matrix.[G]i,jdenotes the(i,j)-th entry of a matrixG.diag{p}means the diagonal matrix with the elements of vectorpon its main diagonal.Finally,CN(0,Ξ)means the complex Gaussian distribution whose mean is zero and variance matrix isΞ.

II.SYSTEM MODEL

Consider an uplink single-cell massive MIMO system consisting of one base station(BS)andKusers.The BS is equipped withNantennas,and the users have one antenna.The received signal vector is

whereP=diag{p1,...,pK} ∈CK×Kis a diagonal matrix representing transmission power of users,whosek-th element on its diagonal represents the transmission power of thek-th user.x=[x1,x2,...,xK]Trepresents the signals of users.n～denotes the noise vector.The same as in[12]and[4],the channel vectorGis modeled as

whereD=diag{β1,...,βK}is the large-scale fading matrix,andH∈CN×Krepresents a small-scale fading channel matrix.Thek-th diagonal element ofDisβk=wherezkrepresents log-normal distributed variables,i.e.,the quantity 10log10(zk) is distributed zero-mean Gaussian random variable,dkis the distance from thek-th user to the BS,dhdenotes the reference distance,andvis the pass loss exponent.βkis slow-varying and known.We consider the Rayleigh fading channel as shown in[13],so each element ofHis modeled as an independent and identically distributed (i.i.d.) complex Gaussian random variable with unit variance and zero mean.Specifically,Hrepresents the combined effect of numerous independent propagation paths in wireless communication.With help of the superposition principle and the central limit theorem,Hwill be approximately Gaussian.

During an uplink training phase,the users transmit mutually orthogonal pilot sequences,which makes the BS able to compute the estimated channelˆGof the local channelG[24].The received training signal matrix is

whereΦis the mutually orthogonal pilot sequences,τPis a coefficient related to the length of the pilot sequences and the pilot transmit power [25],andN～CN(0,IN).

As a result,the MMSE estimation of the channel vectorGis

Then the received signal vector in (1) can be expressed as

The received signal of userkcan be expressed as

Based on(7),we can derive the effective signal-tointerference-plus-noise ratio (SINR) of thek-th user as

With (8),we can obtain thek-th user’s rate as follows:

Correspondingly,the asymptotic rate can be obtained

III.NEAR-OPTIMAL POWER ALLOCATION FOR SE MAXIMIZATION

In this section,based on the derived rate expression,we formulate the optimization problem for SE maximization.To find the feasible region of solution in this problem,we firstly optimize the maximum value of minimal rate of each user.Then,based on the obtained feasible region,a near-optimal algorithm is proposed to find the solution for maximizing the SE of uplink massive MIMO while satisfying minimum rate constraint of each user.

Specifically,subject to maximum power constraint and minimum rate requirement of each user,the SE optimization problem is formulated as follows:

When the channel condition is bad orPmaxis small,the above problem may have no feasible solution since the obtained minRkmay be smaller thanRminunder these cases.For this reason,we need to optimize the following max-min problem to obtain the feasible region of problem(12).

In Appendix,we give the theoretical derivation for solving problem in (13) and obtain the solution of PA.If the obtained solution cannot satisfy minRk ＞Rmin,then the problem(12)will have no feasible solution.Conversely,if the obtained solution satisfies minRk ＞Rmin,then we can solve the problem (12)to attain the solution.

Using the SCA method,the non-convex objective function in(12)is able to be transformed into a convex one by leveraging the following lower-bound of the logarithmic function[27-29].To be specific,we have that

The lower bound of(9)can then be expressed as

With (15),the optimization problem is relaxed and can be converted easily to a convex optimization problem,

Based on the objective function and the constraints in(16),the Lagrangian is formed.By introducing the Lagrange multipliersα,the formulated Lagrangian is expressed as

Lettingyk=ln(pk),(17) can be converted to the sum of linear and concave terms[28],

The BCD method is an effective tool to solve convex problems [30,31],so we will adopt it to solve this problem.In each iteration of the BCD method,a one-dimensional search is performed along coordinate directions at the current point to find the local minimization or maximization.Assuming the other users’powers{pi()}are fixed,we updatepkalternately until the convergence point.

Therefore,the zero point of(19)is rearranged as

Considering the constraints in(12),the near-optimal power of userkis written as

Then the sub-gradient method is used to update the Lagrangian multipliers[32]

wheretis the index of iterations,and the operator[·]+means that if its parameter is negative,it will be zero,otherwise,it will pick the parameter.The iteration step sizeφkis set as square summable step sizes[32].

The whole process of the near-optimal algorithm is summarized in Algorithm 1.

IV.SUBOPTIMAL POWER ALLOCATION FOR SE MAXIMIZATION

In the section above,the proposed algorithm needs three-layer iteration,so its complexity is relatively high.For this reason,the SE optimization problem based on the derived asymptotic analysis is formulated in this section.Similar to the analysis in section III,the max-min problem needs to be solved to find the feasible region and initial value of PA firstly.Then,with these results,a suboptimal algorithm is designed to solve the SE optimization problem,and a suboptimal PA for maximizing the SE performance while satisfying minimum rate constraint is obtained.Then we analyze convergence and complexity of the proposed schemes.The suboptimal algorithm has lower complexity than the near-optimal algorithm,but can obtain SE performance close to that of the latter,as shown in the next section.

4.1 Suboptimal Scheme

WhenNis large,the SE optimization problem can be formulated with the asymptotic SE expression in(11),

Similar to the analysis in the previous section,we need to find the feasible region.Besides,it is worth noting that the BCD method used in this section requires the initial value is within the feasible region.Replaceζkin Appendix A withθk,whereθk=then the PA in Appendix A can be used here to find the initial value.If the solution of the max-min problem cannot satisfy minRk ＞Rmin,the rate constraint cannot be satisfied under this condition.Otherwise,the solution can be used as the initial value of the BCD iteration.

In the massive MIMO system,Nis large in general,so≫1,then we have

Consequently,(23)can be approximated and equivalently expressed as

Lettingtk=logpk,the objective function in (25)can be written as

Differentiate(26)w.r.t.tk,

Setting=0,the obtained solutiont0is

Considering the formulated optimization problem in(23),we convert the constraints into the upper and lower bounds ofpk.Namely,the rate constraint in(23),≥Rmin,can be transformed as

As a result,the problem is converted as

where the lower boundLBkis given below,and the upper boundUBkis shown on the top of the next page.

Assuming the other users’ powers{ti(ik)}are fixed,the BCD method is used to updatetkalternately until the convergence point.Finally,based on the obtained zero pointt0in (28),the solutionfor the problem(33)are achieved,

Finally,the suboptimal PA for the problem are given by

With the above derivation and analysis,the specific procedures are summarized in Algorithm 2.

4.2 Convergence and Complexity Analysis

To begin with,the near-optimal algorithm involves three-layer iterations,thus its convergence relies on the convergence of all these iterations.The convergence of solving PA depends on the convergence of BCD method,which is verified in[31].The iteration of solving the Lagrangian multiplier adopts the subgradient method,and its convergence can be ensured by choosing a proper step size[32].It should be noted that when the number of iterations is large enough,the sub-gradient method of square summable step size will converge to the optimal value[29].The iteration of the outer layer is for SCA method,whose convergence has been studied in [27].Considering that the iterations of the inner layer can converge to the optimal solution,the iteration of the outer layer is ensured to converge to global optimum of problem (16) since(16)is convex problem.The obtained solution is also near-optimal one of original problem(12).To sum up,the near-optimal algorithm is able to converge to nearoptimal solution.

The iteration of solving Lagrange multipliers uses sub-gradient method,and its convergence can be guaranteed by choosing an appropriate step size[32].It is noted that the solution obtained using the sub-gradient method with square summable step sizes comes close to the optimal value with any given tolerance,and when the number of iterations is large enough,it will converge to the optimal value.The convergence of iteration of the outer layer relies on the convergence of SCA,which has been carefully investigated in [27].It is shown that SCA guarantees a global optimum mostly.Considering that the iterations of the inner layer can converge to the optimal solution,the iteration of the outer layer is guaranteed to converge to global optimum.To sum up,the near-optimal algorithm is able to converge to global optimum.

Here,we compare the complexity of the nearoptimal scheme,suboptimal scheme and the benchmark,i.e.,particle swarm optimization(PSO)scheme[33].To be specific,all these three schemes need to calculate the powers ofKusers in the innermost iteration,thus the complexity for this isK.In the nearoptimal scheme,we set that the iterations of BCD method needI1times to converge,the iterations of the sub-gradient method needI2times to converge,and that of the SCA method needsI3times to converge.Thus,the complexity for the near-optimal scheme is O(KI1I2I3).In the suboptimal scheme,we denote the number of iterations for the BCD method to converge asI4.Therefore,the complexity for the suboptimal scheme is O(KI4).Finally,we denote the number of iterations of the PSO scheme asI5,and the particle swarm size isM.Hence,the complexity for the PSO scheme isO(MI5Kln(K)) [34].It is found that the complexity of the near-optimal scheme is lower than that of the PSO scheme,but the nearoptimal scheme provides SE performance close to that of the PSO scheme as shown in section VI.The complexity of the suboptimal scheme is the lowest in that it needs only one-layer iteration,but the SE performance of the suboptimal scheme is close to that of the nearoptimal scheme,especially whenNis large.

V.PILOT AND DATA POWER ALLOCATION

In the above two section,we only give the optimization of data power of each user,while the pilot power is fixed.Thus,the increase of SE performance will be limited.For this reason,in this section,we present the joint design of pilot and data power to further improve the system SE,and propose an iterative algorithm to find the suboptimal joint PA.

wherepmaxis maximum transmit power for each user,i.e.,it is the upper bound of sum of the user’s data power and pilot power.

Similar to the analysis in the previous sections,we need to find the feasible region of solution.Based on this,we give the max-min problem of rate and the corresponding solution in Appendix B.When the feasible region is found,the problem(38)has solution,otherwise the problem(38)has no solution.

Since the objective and constraints in(38)involves the product ofpp,kandpk,it is difficult to find the solution directly.Therefore,the BCD method is used to tackle the problem.That is,the optimization is divided into two stage.In the first stage,the pilot powerpp,kis optimized give the data powerpk,and in the second stage,the data powerpkis optimized given the pilot powerpp,kuntil they can converge.

In the first stage,it is found that the numerator of the SINR increases monotonically with respect topp,k,and the denominator decreases monotonically with respect topp,k.Moreover,to achieve the maximum SE,the numerator and denominator of objective function in(38)need to be maximized and minimized,respectively.Hence,pp,kshould take the maximum value,

In the second stage,we assume that the pilot power is fixed,then the problem is the same as the one in Section III.We replace the power limitPmaxin (12)withpmax-pp,k,and replace theandwithandthen Algorithm 1 can be used to solve this problem.

Additionally,if there is no minimum rate constraint,the Lagrangian method can be omitted.Correspondingly,the iteration for sub-gradient method can be eliminated.Hence,the algorithm for PA without minimum rate constraint is simpler than that with minimum rate constraint.However,the minimum rate constraint is essential for guaranteeing the QoS of users.That is why we take it into account.

The whole process of the pilot and data PA algorithm is summarized in Algorithm 3.

VI.SIMULATION RESULTS

In this section,we present simulation results for evaluating the performance of the proposed algorithms.In order to exhibit the validity of the proposed schemes,we introduce the PSO scheme [33] as a benchmark.We set the cellular as a circle.

Users are evenly distributed in the cell.zkis lognormal distributed variables with zero mean,and its standard derivation is 8 dB.The coefficient related to the length of the pilot sequences and the pilot transmit powerτPis set as 10 dB[13,14,25].The other main default parameters are presented in Table 1.Simulation results are depicted in Figures 1-5 below.

Table 1.The system parameters.

In Figure 1,SE performance in massive MIMO systems with differentNis shown,wherePmax=4×10-5W,0.004W,respectively.As shown in Figure 1,the SE performance of massive MIMO system is improved asNincreases.The reason is that the largerNis,the greater the spatial diversity gain is.Moreover,the SE performance of the near-optimal scheme is coincident with that of the benchmark,i.e.,the PSO scheme.Besides,the suboptimal scheme,which has lower complexity,offers the performance similar to that of the benchmark.Especially for largerN,its performance becomes nearly the same as the latter.But whenNis small,SE performance of the suboptimal scheme is slightly lower than that of the PSO scheme,which is consistent with the analysis in Section IV.

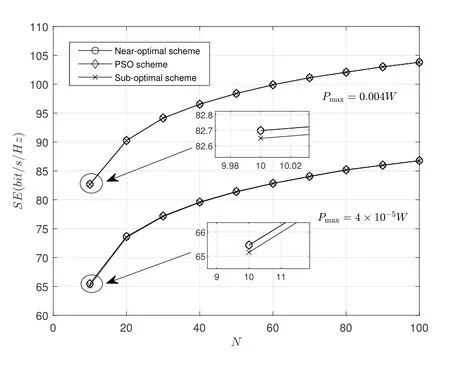
Figure 1.SE comparison of massive MIMO system with different N.

Figure 2 depicts SE performance in massive MIMO systems with differentK,and performance comparison with the scheme in [22] is given.As shown in Figure 2,the suboptimal scheme is able to achieve SE performance almost the same as that of the benchmark and the near-optimal scheme,with low complexity.In addition,the SE performance of the near-optimal scheme approaches that of the benchmark,but its complexity is lower.It is found that the PA is less constrained with morePmax,leading to higher SE.Besides,the slopes of the curves decrease with the increasingPmax.The reason is that the PA is gradually approaching to the optimal PA without power constraint.What’s more,the system SE improves with the improvement ofKfor the these three schemes,i.e.,the system withK=5 has higher SE than that withK=3,as expected.Finally,we can find that our proposed schemes have nearly the same performance as the algorithm in [22],and for each simulation,the average run time of the proposed near-optimal and suboptimal schemes is 0.0693 s and 0.0012 s,respectively,while the average run time of algorithm in[22]is 10.5726 s.Thus,our proposed schemes provide similar performance with that in [22],but with much lower time complexity.

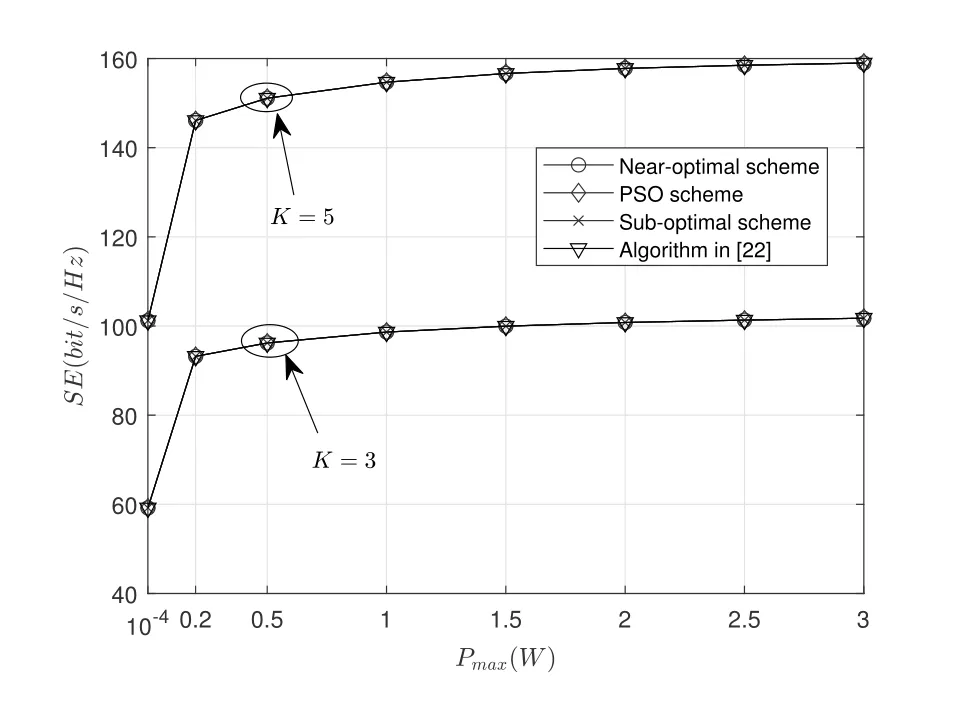
Figure 2.SE comparison of massive MIMO system with different K.

Figure 3 presents SE performance with different rate constraints under massive MIMO systems.The same as the above figures,the suboptimal scheme is able to obtain the performance similar to that of the benchmark and the near-optimal scheme with low complexity.Moreover,the slopes of the curves decrease with the increasingPmax,which is because the PA is gradually approaching to the optimal PA without power constraint.Besides,whenRmin=5 bit/s/Hz,the SE is lower than that ofRmin=3 bits/s/Hz,and the SE ofRmin=3 bit/s/Hz is lower than that ofRmin=0 bit/s/Hz,which is equal to optimize PA with no rate constraint.It is because with higher QoS requirement,more power of each user is used to satisfy the QoS constraint,which leads to a decrease in SE.For example,whenRmin=0 bit/s/Hz,the maximum power for each user isPmax,but whenRmin=3 bit/s/Hz orRmin=5 bit/s/Hz,the maximum power that can be assigned to some users is less thanPmax.In addition,it is impossible to satisfy high QoS requirement under certain poor channel conditions,and the corresponding SE is 0 bit/s/Hz.As a result,the SE performance becomes lower with higher QoS requirement.

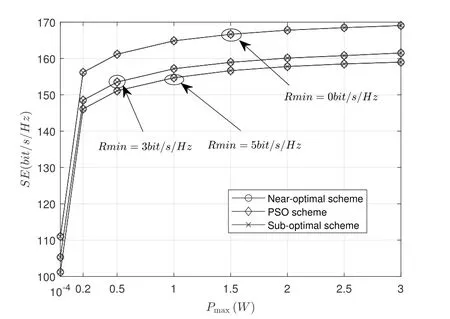
Figure 3.SE comparison of massive MIMO system with different rate constraints.

Figure 4 evaluates the convergence speed of the proposed schemes,wherePmax=1.5W.From Figure 4,it is found that the convergence of Algorithm 1 and Algorithm 2 can be guaranteed.It can be seen that near-optimal scheme converges to the optimum value within 60 iterations,while the suboptimal scheme algorithm needs only about 2 iterations to converge.Besides,it is shown that the convergence speed of the PSO scheme is slow.The PSO scheme needs more than 100 iterations to converge,thus,its convergence point is not shown in the figure for convenience.In conclusion,Figure 4 is consistent with the analysis in Section IV.

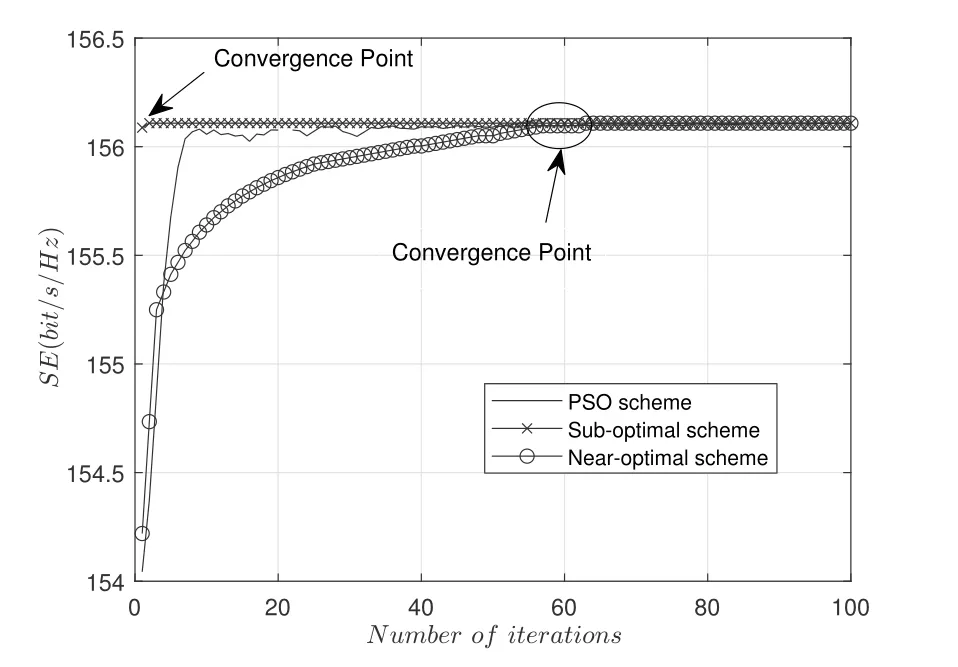
Figure 4.The convergence speed of different schemes.

Figure 5 compares the SE performance of Algorithm 3 and Algorithm 1,whereRmin=2bit/s/Hz,and the PSO scheme is selected as the benchmark.For fair comparison,the abscissapmaxis the sum of pilot power and data power.From Figure 5,it is found that the curves of Algorithm 3 and Algorithm 1 are consistent with that of the PSO scheme,which verifies their effectiveness.Besides,the system SE with joint design of pilot and data power is obviously higher than that with only optimizing the data power and the fixed pilot power.The reason is that the former can optimize the pilot power and data power well,so that the pilot power is allocated reasonably,thereby optimizing the performance of channel estimation,while the latter uses the fixed pilot power.As a result,superior SE performance is achieved.

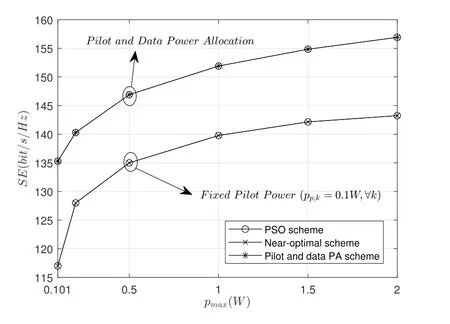
Figure 5.SE of massive MIMO system with pilot and data power allocation.

VII.CONCLUSION

The SE performance of uplink massive MIMO system with imperfect CSI is studied over Rayleigh fading channel,and the corresponding SE and its asymptotical expression are deduced.With these results,the optimization problem to maximize the SE is formulated with maximum power and minimum rate requirements.A near-optimal PA scheme is proposed based on the SCA method,BCD method and sub-gradient method.As shown in the simulation results,the nearoptimal PA scheme is able to obtain almost the same SE performance as that of the benchmark,but with lower complexity.This scheme involves three iterations.For this reason,a low-complexity suboptimal scheme is proposed based on the asymptotic SE expression by using the characteristic of massive MIMO systems and BCD method,and it only needs onelayer iteration.Moreover,it has the SE performance close to that of the PSO scheme.Besides,the nearoptimal scheme requires timely CSI feedback since the obtained PA is related to the small-scale channel information.Whereas for the suboptimal scheme,it is only related to the large-scale channel information.Thus,instantaneous CSI feedback is avoided.Hence,the suboptimal scheme can obtain the effective tradeoff between the performance and complexity,and has more practical value.Finally,we give the joint design of the pilot and data powers to further improve the system SE,and an effective algorithm is proposed to find the suboptimal solution of joint design.Simulation results indicate that near-optimal scheme provides nearly the same SE performance to that of the benchmark scheme,and the suboptimal scheme also obtain the SE close to the near-optimal scheme,especially for largeN.Besides,by jointly optimizing the pilot power and data power,the system SE is obviously increased,and it is higher than that of the proposed schemes with only optimizing the data power since the pilot power is fixed and not optimized for the latter.

ACKNOWLEDGEMENT

This work was supported by the Fundamental Research Funds for the Central Universities of NUAA(No.kfjj20200414),Natural Science Foundation of Jiangsu Province in China(No.BK20181289).

APPENDIX

Appendix A

In this Appendix,we solve the optimization problem in (13).Without loss of generality,we setRl=minRk,namely,

Appendix B

In this Appendix,we give the optimization problem of max-min of user rate by considering the joint design of data and pilot power.

The problem is equivalent to maximize the minimum SINR,

Since the objective and constraints in(B.2)involves the product ofpp,kandpk,it is difficult to find the solution directly.Hence,the BCD method is used to solve the problem.We divide the optimization into two stages.Firstly,give the pilot power,the problem is reduced to the one in Appendix A.Hence,the power allocation is given by

After that,pp,kis optimized given the data powerpk.Correspondingly,the optimization problem can be formulated as

and it is equivalent to

The problem in(B.5) can be solved by minimizing the denominator,which decreases monotonically with respect topp,k.Based on this,pp,ktakes the maximum value,i.e.,pp,k=pmax-pk.

In terms of the BCD method,repeating the above two stages until the PA of data and pilot converges.After that,we can obtain the suboptimal solution